הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/29.5.11"
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
מ |
מ (←דוגמאות) |
||
| שורה 29: | שורה 29: | ||
# גם <math>f(x)=f'(x)</math> היא מד"ר, ופתרונה <math>f(x)=ae^x</math> עבור קבוע a. | # גם <math>f(x)=f'(x)</math> היא מד"ר, ופתרונה <math>f(x)=ae^x</math> עבור קבוע a. | ||
# <math>f''(x)=-f(x)</math>. ניתן להוכיח שכל הפתרונות האפשריים הם מהצורה <math>a\sin(x)+b\cos(x)</math> עבור a,b קבועים. | # <math>f''(x)=-f(x)</math>. ניתן להוכיח שכל הפתרונות האפשריים הם מהצורה <math>a\sin(x)+b\cos(x)</math> עבור a,b קבועים. | ||
| − | # {{הערה|(דוגמה יותר קשה)}} נמצא פתרון כללי ל-<math>f''(x)-xf(x)=0</math> וגם פתרון כך ש-<math>f(0)=3\ \and\ f'(0)=-2</math>: נעיר שניתן להוכיח שהפתרון אינו פונקציה אלמנטרית ולכן אין טעם לנחש. במקום, נניח שיש פתרון מהסוג <math>f(x)=\sum_{n=0}^\infty a_nx^n</math> עם רדיוס התכנסות <math>R>0</math>. לפיכך <math>f''(x)=\sum_{n=2}^\infty n(n-1)(x-x_0)^{n-2}</math>. צריך להתקיים <math>f''(x)=xf(x)</math> ולכן <math>\sum_{n=2}^\infty n(n-1)a_nx^{n-2}=\sum_{n=0}^\infty a_nx^{n+1}</math> ולאחר הזזת אינדקסים נקבל: <math>\sum_{n=0}^\infty (n+2)(n+1)a_{n+2}x^n=\sum_{n=1}^\infty a_{n-1}x^n</math>. <span id="continue"><!--נא לא למחוק span זה--></span>{{הערה|את ההמשך עשינו ב[[משתמש:אור שחף/133 - הרצאה/31.5.11|הרצאה שאחריה]]:}} ממשפט היחידות לטורי חזקות מתקיים <math>2a_2=0\ \and\ \forall n\ge1:\ (n+2)(n+1)a_{n+2}=a_{n-1}</math>. מכאן ש-<math>a_0,a_1</math> קבועים כלשהם, <math>a_2=0</math>, ו-<math>a_{n+2}=\frac{a_{n-1}}{(n+2)(n+1)}</math>, לכן <math>a_3=\frac{a_1}{3\cdot2},\ a_4=\frac{a_1}{4\cdot3},\ a_5=0,\ a_6=\frac{a_3}{6\cdot5}=\frac{a_0}{6\cdot5\cdot3\cdot2},\ a_7=\frac{a_1}{7\cdot6\cdot4\cdot3},\ a_8=0,\ \dots</math>. מכאן נובע ש-{{left|<math>\begin{align}f(x)&=\sum_{n=0}^\infty a_nx^n\\&=a_0+a_1x+\frac{a_1}{3\cdot2}x^3+\frac{a_1}{4\cdot3}x^4+\frac{a_0}{6\cdot5\cdot3\cdot2}x^6+\frac{a_1}{7\cdot6\cdot4\cdot3}x^7+\dots\\&=a_0\left(1+\frac{x^3}{3\cdot2}+\frac{x^5}{6\cdot5\cdot3\dot2}+\dots\right)+a_1\left(x+\frac{x^4}{4\cdot3}+\frac{x^7}{7\cdot6\cdot4\cdot3}+\dots\right)\end{align}</math>}}נבדוק שהטורים האלה מתכנסים: בטור שמוכפל ב-<math>a_0</math>, היחס בין שני איברים עוקבים הוא <math>\frac{\frac{x^{3n}}{3n(3n-1)(3n-3)(3n-4)\cdots}}{\frac{x^{3n-3}}{(3n-3)(3n-4)\cdots}}=\frac{x^3}{3n(3n-1)}</math>, ששואף ל-0, ולכן רדיוס ההתכנסות הוא (ממבחן המנה) <math>\infty</math>. באופן דומה מקבלים שרדיוס ההתכנסות של הטור המוכפל ב-<math>a_1</math> הוא <math>\infty</math> ולכן <math>f(x)</math> הנ"ל מוגדרת לכל x כך ש-<math>|x-0|<\infty</math>, כלומר <math>x\in\mathbb R</math>. לפי משפט 4 טורים אלו גזירים אינסוף פעמים ובפרט פעמיים ב-<math>\mathbb R</math>. כמו כן נעיר שניתן להוכיח שקיבלנו את הפתרון הכללי למד"ר, ולכן נותר רק לבדוק מתי <math>f(0)=3\ \and\ f'(0)=-2</math>: נזכר ש-<math>\forall n:\ a_n=\frac{f^{(n)}(x_0)}{n!}</math> ולכן <math>3=f^{(0)}(0)=0!a_0 | + | # {{הערה|(דוגמה יותר קשה)}} נמצא פתרון כללי ל-<math>f''(x)-xf(x)=0</math> וגם פתרון כך ש-<math>f(0)=3\ \and\ f'(0)=-2</math>: נעיר שניתן להוכיח שהפתרון אינו פונקציה אלמנטרית ולכן אין טעם לנחש. במקום, נניח שיש פתרון מהסוג <math>f(x)=\sum_{n=0}^\infty a_nx^n</math> עם רדיוס התכנסות <math>R>0</math>. לפיכך <math>f''(x)=\sum_{n=2}^\infty n(n-1)(x-x_0)^{n-2}</math>. צריך להתקיים <math>f''(x)=xf(x)</math> ולכן <math>\sum_{n=2}^\infty n(n-1)a_nx^{n-2}=\sum_{n=0}^\infty a_nx^{n+1}</math> ולאחר הזזת אינדקסים נקבל: <math>\sum_{n=0}^\infty (n+2)(n+1)a_{n+2}x^n=\sum_{n=1}^\infty a_{n-1}x^n</math>. <span id="continue"><!--נא לא למחוק span זה--></span>{{הערה|את ההמשך עשינו ב[[משתמש:אור שחף/133 - הרצאה/31.5.11|הרצאה שאחריה]]:}} ממשפט היחידות לטורי חזקות מתקיים <math>2a_2=0\ \and\ \forall n\ge1:\ (n+2)(n+1)a_{n+2}=a_{n-1}</math>. מכאן ש-<math>a_0,a_1</math> קבועים כלשהם, <math>a_2=0</math>, ו-<math>a_{n+2}=\frac{a_{n-1}}{(n+2)(n+1)}</math>, לכן <math>a_3=\frac{a_1}{3\cdot2},\ a_4=\frac{a_1}{4\cdot3},\ a_5=0,\ a_6=\frac{a_3}{6\cdot5}=\frac{a_0}{6\cdot5\cdot3\cdot2},\ a_7=\frac{a_1}{7\cdot6\cdot4\cdot3},\ a_8=0,\ \dots</math>. מכאן נובע ש-{{left|<math>\begin{align}f(x)&=\sum_{n=0}^\infty a_nx^n\\&=a_0+a_1x+\frac{a_1}{3\cdot2}x^3+\frac{a_1}{4\cdot3}x^4+\frac{a_0}{6\cdot5\cdot3\cdot2}x^6+\frac{a_1}{7\cdot6\cdot4\cdot3}x^7+\dots\\&=a_0\left(1+\frac{x^3}{3\cdot2}+\frac{x^5}{6\cdot5\cdot3\dot2}+\dots\right)+a_1\left(x+\frac{x^4}{4\cdot3}+\frac{x^7}{7\cdot6\cdot4\cdot3}+\dots\right)\end{align}</math>}}נבדוק שהטורים האלה מתכנסים: בטור שמוכפל ב-<math>a_0</math>, היחס בין שני איברים עוקבים הוא <math>\frac{\frac{x^{3n}}{3n(3n-1)(3n-3)(3n-4)\cdots}}{\frac{x^{3n-3}}{(3n-3)(3n-4)\cdots}}=\frac{x^3}{3n(3n-1)}</math>, ששואף ל-0, ולכן רדיוס ההתכנסות הוא (ממבחן המנה) <math>\infty</math>. באופן דומה מקבלים שרדיוס ההתכנסות של הטור המוכפל ב-<math>a_1</math> הוא <math>\infty</math> ולכן <math>f(x)</math> הנ"ל מוגדרת לכל x כך ש-<math>|x-0|<\infty</math>, כלומר <math>x\in\mathbb R</math>. לפי משפט 4 טורים אלו גזירים אינסוף פעמים ובפרט פעמיים ב-<math>\mathbb R</math>. כמו כן נעיר שניתן להוכיח שקיבלנו את הפתרון הכללי למד"ר, ולכן נותר רק לבדוק מתי <math>f(0)=3\ \and\ f'(0)=-2</math>: נזכר ש-<math>\forall n:\ a_n=\frac{f^{(n)}(x_0)}{n!}</math> ולכן <math>3=f^{(0)}(0)=0!a_0</math>, כלומר <math>a_0=3</math> וגם <math>-2=f^{(1)}(0)=1!a_1</math>, כלומר <math>a_1=-2</math>. מציבים ערכים אלו של <math>a_1,a_0</math> בפתרון הכללי שמצאנו ל-<math>f(x)</math> וסיימנו את התרגיל. {{משל}} |
גרסה מ־20:32, 25 ביוני 2011
את משפט 3 לא סיימנו בהרצאה הקודמת ולכן השלמנו אותו ב-24.5.11. חלק זה מופיע בסיכום ההרצאה הקודמת ולא בדף הנוכחי.
תוכן עניינים
טורי חזקות (המשך)
משפט 4
נניח שלטור 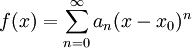 יש רדיוס התכנסות
יש רדיוס התכנסות 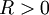 , אזי:
, אזי:
- f גזירה אינסוף פעמים בקטע
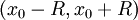 ולכל
ולכל 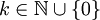 מתקיים
מתקיים 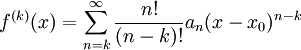 . רדיוס ההתכנסות של הטורים הגזור הוא R.
. רדיוס ההתכנסות של הטורים הגזור הוא R. - לכל
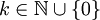 ,
, 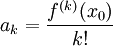 , ז"א הטור הוא טור טיילור של f סביב
, ז"א הטור הוא טור טיילור של f סביב  .
.
הוכחה
- באינדוקציה, בעזרת משפט 3.
- הוכחנו בסעיף 1 ש-
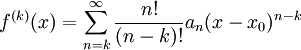 . נציב
. נציב 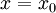 ונקבל
ונקבל 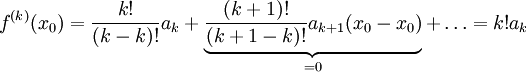 , כלומר
, כלומר 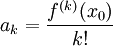 .
. 
מסקנה (משפט היחידות לטורי חזקות)
נניח ששני טורי חזקות בקטע שלם, כלומר 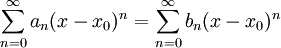 לכל
לכל 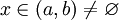 , אזי
, אזי 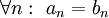 .
.
הוכחה
נגדיר פונקציה גבולית 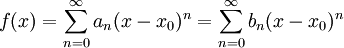 .
עפ"י סעיף 2 של משפט 4 מתקיים
.
עפ"י סעיף 2 של משפט 4 מתקיים 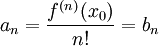 .
. 
הערה
חשוב לא להתבלבל: יתכן בהחלט מצב בו 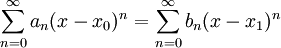 אבל
אבל 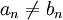 עבור n כלשהו.
עבור n כלשהו.
דוגמאות
- נמצא טור מקלורין של
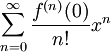 עבור הפונקציה
עבור הפונקציה 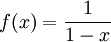 : ידוע לנו ש-
: ידוע לנו ש-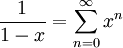 עבור
עבור 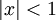 . לפי משפט 4 טור זה הוא בהכרח טור טיילור של f סביב 0, כלומר זה טור מקלורן של f.
. לפי משפט 4 טור זה הוא בהכרח טור טיילור של f סביב 0, כלומר זה טור מקלורן של f. 
- נמצא טור טיילור של
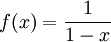 סביב
סביב 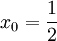 , ז"א
, ז"א 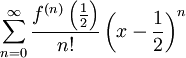 .
.
דרך 1:נציב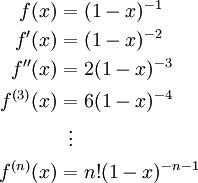
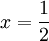 לקבל
לקבל 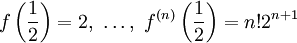 ולכן הטור הוא
ולכן הטור הוא 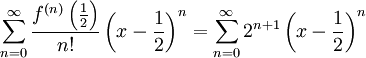 . לצערנו עדיין לא ניתן לדעת בוודאות שהטור אכן מתכנס ל-f כי לא וידאנו שהשארית שואפת ל-0.
. לצערנו עדיין לא ניתן לדעת בוודאות שהטור אכן מתכנס ל-f כי לא וידאנו שהשארית שואפת ל-0.
דרך 2: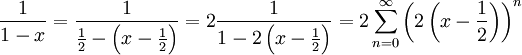 . בניסיון השני קיבלנו את אותה התוצאה מהר יותר, והפעם אנו גם יודעים שהטור מתכנס ל-f כאשר
. בניסיון השני קיבלנו את אותה התוצאה מהר יותר, והפעם אנו גם יודעים שהטור מתכנס ל-f כאשר 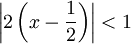 , כלומר כש-
, כלומר כש-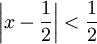 .
. 
נסכם: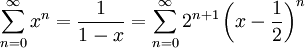 בקטע
בקטע 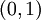 ויש כאן שני טורי חזקות שונים לגמרי שמתכנסים לאותה פונקציה. זה לא סותר את משפט היחידות כי לטורים אלה יש מרכז שונה.
ויש כאן שני טורי חזקות שונים לגמרי שמתכנסים לאותה פונקציה. זה לא סותר את משפט היחידות כי לטורים אלה יש מרכז שונה. - נמצא את טור מקלורין של
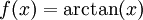 , ונקבע את תחום ההתכנסות של הטור ל-f.
, ונקבע את תחום ההתכנסות של הטור ל-f.
דרך 1: טור מקלורין הוא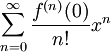 , כאשר מכאן ואילך לא נעים לגזור, ולכן נוותר על הדרך הזו.
, כאשר מכאן ואילך לא נעים לגזור, ולכן נוותר על הדרך הזו.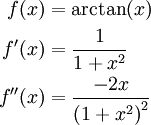
דרך 2: תחילה נחשב טור מקלורין לפונקציה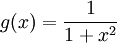 ואז נוכל לקבל את הטור עבור
ואז נוכל לקבל את הטור עבור 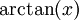 ע"י אינגרציה איבר-איבר. כעת:
ע"י אינגרציה איבר-איבר. כעת: 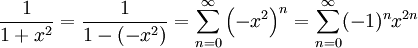 עבור
עבור 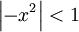 , ז"א
, ז"א 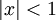 . עתה נעשה אינטגרציה:
. עתה נעשה אינטגרציה: 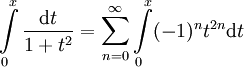 לכל
לכל 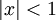 , ולכן
, ולכן 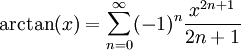 . עפ"י משפט היחידות לטורי חזקות נסיק שזה טור מקלורין של
. עפ"י משפט היחידות לטורי חזקות נסיק שזה טור מקלורין של 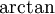 בתחום
בתחום 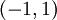 .
.  אם מותר להציב
אם מותר להציב 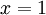 אז נקבל את המשוואה היפה
אז נקבל את המשוואה היפה 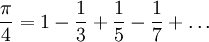 , אבל מכיוון שלא מתקיים
, אבל מכיוון שלא מתקיים 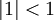 צריך להוכיח זאת (את ההוכחה ניתן בהרצאה הבאה). עם זאת, ניתן כבר עכשיו לדעת בוודאות ש-
צריך להוכיח זאת (את ההוכחה ניתן בהרצאה הבאה). עם זאת, ניתן כבר עכשיו לדעת בוודאות ש-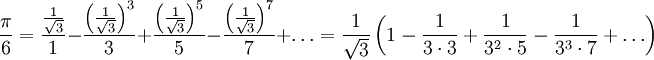 .
. - מצאו את טור טיילור ל-
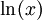 סביב
סביב 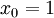 וקבעו באיזה תחום הטור מתכנס ל-
וקבעו באיזה תחום הטור מתכנס ל-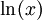 .
.
דרך 1: לפי הנוסחה לטור טיילור נקבל ואז נבדוק מתי השארית
ואז נבדוק מתי השארית 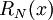 שואפת ל-0.
שואפת ל-0.
דרך 2: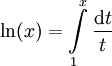 ולכן תחילה נפתח
ולכן תחילה נפתח  :
: 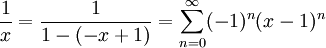 כאשר
כאשר 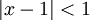 . כעת
. כעת 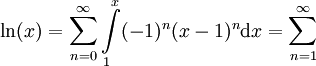 בתחום
בתחום 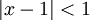 .
.  עבור
עבור 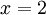 לא מתקיים
לא מתקיים 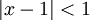 , אבל אם בכל זאת ההצבה הזו נכונה אז נקבל
, אבל אם בכל זאת ההצבה הזו נכונה אז נקבל 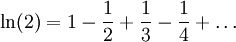 (בהרצאה הבאה נוכיח שזה נכון).
(בהרצאה הבאה נוכיח שזה נכון). - (תרגיל ממבחן) נגדיר
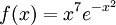 . מצאו
. מצאו 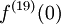 : לכל
: לכל 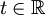 מתקיים
מתקיים 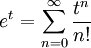 ונציב
ונציב 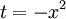 לקבל
לקבל 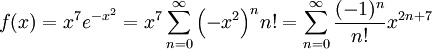 . לפי משפט 4 מתקיים המקדם
. לפי משפט 4 מתקיים המקדם 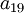 של
של 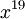 מקיים
מקיים 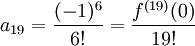 ולכן
ולכן 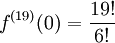 .
. 
מבוא למשוואות דיפרנציאליות רגילות (מד"ר)
הגדרה: מד"ר היא משוואה המקשרת, פונקציה נעלמת, נגזרותיה העוקבות ופונקציות אחרות ידועות.
דוגמאות
-
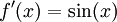 היא מד"ר, שפתרונה הוא
היא מד"ר, שפתרונה הוא 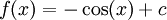 עבור קבוע c כלשהו.
עבור קבוע c כלשהו. - גם
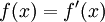 היא מד"ר, ופתרונה
היא מד"ר, ופתרונה 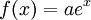 עבור קבוע a.
עבור קבוע a. -
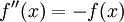 . ניתן להוכיח שכל הפתרונות האפשריים הם מהצורה
. ניתן להוכיח שכל הפתרונות האפשריים הם מהצורה 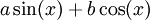 עבור a,b קבועים.
עבור a,b קבועים. - (דוגמה יותר קשה) נמצא פתרון כללי ל-
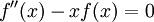 וגם פתרון כך ש-
וגם פתרון כך ש-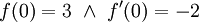 : נעיר שניתן להוכיח שהפתרון אינו פונקציה אלמנטרית ולכן אין טעם לנחש. במקום, נניח שיש פתרון מהסוג
: נעיר שניתן להוכיח שהפתרון אינו פונקציה אלמנטרית ולכן אין טעם לנחש. במקום, נניח שיש פתרון מהסוג 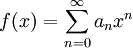 עם רדיוס התכנסות
עם רדיוס התכנסות 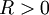 . לפיכך
. לפיכך 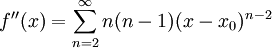 . צריך להתקיים
. צריך להתקיים 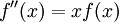 ולכן
ולכן 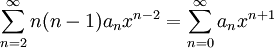 ולאחר הזזת אינדקסים נקבל:
ולאחר הזזת אינדקסים נקבל: 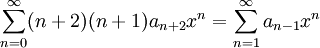 . את ההמשך עשינו בהרצאה שאחריה: ממשפט היחידות לטורי חזקות מתקיים
. את ההמשך עשינו בהרצאה שאחריה: ממשפט היחידות לטורי חזקות מתקיים  . מכאן ש-
. מכאן ש-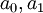 קבועים כלשהם,
קבועים כלשהם, 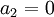 , ו-
, ו-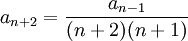 , לכן
, לכן 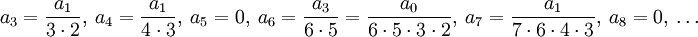 . מכאן נובע ש-נבדוק שהטורים האלה מתכנסים: בטור שמוכפל ב-
. מכאן נובע ש-נבדוק שהטורים האלה מתכנסים: בטור שמוכפל ב-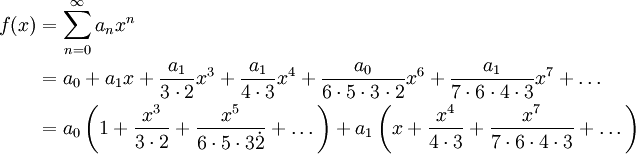
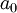 , היחס בין שני איברים עוקבים הוא
, היחס בין שני איברים עוקבים הוא 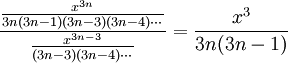 , ששואף ל-0, ולכן רדיוס ההתכנסות הוא (ממבחן המנה)
, ששואף ל-0, ולכן רדיוס ההתכנסות הוא (ממבחן המנה) 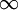 . באופן דומה מקבלים שרדיוס ההתכנסות של הטור המוכפל ב-
. באופן דומה מקבלים שרדיוס ההתכנסות של הטור המוכפל ב-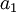 הוא
הוא 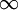 ולכן
ולכן  הנ"ל מוגדרת לכל x כך ש-
הנ"ל מוגדרת לכל x כך ש-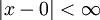 , כלומר
, כלומר 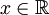 . לפי משפט 4 טורים אלו גזירים אינסוף פעמים ובפרט פעמיים ב-
. לפי משפט 4 טורים אלו גזירים אינסוף פעמים ובפרט פעמיים ב-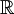 . כמו כן נעיר שניתן להוכיח שקיבלנו את הפתרון הכללי למד"ר, ולכן נותר רק לבדוק מתי
. כמו כן נעיר שניתן להוכיח שקיבלנו את הפתרון הכללי למד"ר, ולכן נותר רק לבדוק מתי 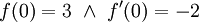 : נזכר ש-
: נזכר ש-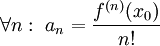 ולכן
ולכן 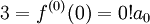 , כלומר
, כלומר 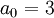 וגם
וגם 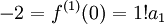 , כלומר
, כלומר 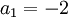 . מציבים ערכים אלו של
. מציבים ערכים אלו של 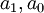 בפתרון הכללי שמצאנו ל-
בפתרון הכללי שמצאנו ל- וסיימנו את התרגיל.
וסיימנו את התרגיל. 