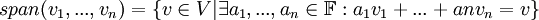הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/5"
מתוך Math-Wiki
(יצירת דף עם התוכן "=צירופים לינאריים, תלות לינארית ומרחבים נפרשים (span)= ==הגדרת צירוף לינארי== יהי V מ"ו מעל שדה <...") |
(←הגדרת צירוף לינארי) |
||
| שורה 3: | שורה 3: | ||
==הגדרת צירוף לינארי== | ==הגדרת צירוף לינארי== | ||
יהי V מ"ו מעל שדה <math>\mathbb{F}</math> ויהיו <math>v_1,...,v_n\in V</math> וקטורים במרחב. '''צירוף לינארי''' של <math>v_1,...,v_n</math> הינו '''וקטור במרחב''' <math>v\in V</math> כך שקיימים סקלרים בשדה <math>a_1,...,a_n\in\mathbb{F}</math> המקיימים <math>v=a_1v_1+...+a_nv_n</math>. | יהי V מ"ו מעל שדה <math>\mathbb{F}</math> ויהיו <math>v_1,...,v_n\in V</math> וקטורים במרחב. '''צירוף לינארי''' של <math>v_1,...,v_n</math> הינו '''וקטור במרחב''' <math>v\in V</math> כך שקיימים סקלרים בשדה <math>a_1,...,a_n\in\mathbb{F}</math> המקיימים <math>v=a_1v_1+...+a_nv_n</math>. | ||
| + | ==הגדרת המרחב הנפרש (span)== | ||
| + | בתנאי ההגדרה לעיל; '''המרחב הנפרש''' על ידי הוקטורים <math>v_1,...,v_n</math> מוגדר להיות '''קבוצת (אוסף) כל הצירופים הלינאריים''' של הוקטורים הללו. כלומר, <math>span(v_1,...,v_n)=\{v\in V|\exists a_1,...,a_n\in\mathbb{F}:a_1v_1+...+anv_n=v\}</math> | ||
גרסה מ־11:14, 29 ביולי 2011
צירופים לינאריים, תלות לינארית ומרחבים נפרשים (span)
הגדרת צירוף לינארי
יהי V מ"ו מעל שדה  ויהיו
ויהיו 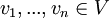 וקטורים במרחב. צירוף לינארי של
וקטורים במרחב. צירוף לינארי של 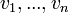 הינו וקטור במרחב
הינו וקטור במרחב 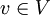 כך שקיימים סקלרים בשדה
כך שקיימים סקלרים בשדה 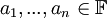 המקיימים
המקיימים 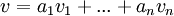 .
.
הגדרת המרחב הנפרש (span)
בתנאי ההגדרה לעיל; המרחב הנפרש על ידי הוקטורים 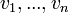 מוגדר להיות קבוצת (אוסף) כל הצירופים הלינאריים של הוקטורים הללו. כלומר,
מוגדר להיות קבוצת (אוסף) כל הצירופים הלינאריים של הוקטורים הללו. כלומר,