הבדלים בין גרסאות בדף "88-133 אינפי 2 תשעב סמסטר ב/תרגילים/תרגיל 3"
מתוך Math-Wiki
(←5) |
(←2) |
||
| (2 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
==1== | ==1== | ||
===א=== | ===א=== | ||
| − | חשב את אורך העקום של הפונקציה <math>f(x)=\frac{e^x+e^{-x}}{2}</math> בקטע <math>[a,b]</math> | + | חשב את [[אורך עקומה|אורך העקום]] של הפונקציה <math>f(x)=\frac{e^x+e^{-x}}{2}</math> בקטע <math>[a,b]</math> |
===ב=== | ===ב=== | ||
| − | תהי f גזירה על כל הממשיים. הוכח שלכל M>0 קיים קטע <math>[a,b]</math> כך | + | תהי f גזירה ברציפות על כל הממשיים. הוכח שלכל M>0 קיים קטע <math>[a,b]</math> כך ש[[אורך עקומה|אורך העקומה]] של הפונקציה בקטע זה גדול מ-M. |
==2== | ==2== | ||
| שורה 10: | שורה 10: | ||
תהי f רציפה ב<math>[a,b]</math> הוכח כי | תהי f רציפה ב<math>[a,b]</math> הוכח כי | ||
| − | ::<math>\lim_{n\rightarrow\infty}\int_a^b|f(x)|^{\frac{1}{n}}=\max_{x\in [a,b]}|f(x)|</math> | + | ::<math>\lim_{n\rightarrow\infty}\Big[\int_a^b|f(x)|^ndx\Big]^{\frac{1}{n}}=\max_{x\in [a,b]}|f(x)|</math> |
==3== | ==3== | ||
גרסה אחרונה מ־20:29, 28 באפריל 2012
1
א
חשב את אורך העקום של הפונקציה  בקטע
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
ב
תהי f גזירה ברציפות על כל הממשיים. הוכח שלכל M>0 קיים קטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך שאורך העקומה של הפונקציה בקטע זה גדול מ-M.
כך שאורך העקומה של הפונקציה בקטע זה גדול מ-M.
2
תהי f רציפה ב![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוכח כי
הוכח כי
3
תהי f רציפה. לכל אפסילון גדול מאפס נגדיר את הפונקציה
א
הוכח כי 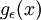 גזירה
גזירה
ב
הוכח כי לכל x מתקיים 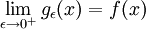
4
הוכח כי למשוואה  יש פתרון אחד ויחיד. מהו?
יש פתרון אחד ויחיד. מהו?
5
נניח f פונקציה רציפה, אי שלילית כך שלכל שתי נקודות בקטע ![x,y\in [0,2]](/images/math/3/5/2/352b095ced782b62fe85c587bab73c5b.png) ולכל
ולכל ![t\in [0,1]](/images/math/d/9/a/d9a06fde4663cdd5b1ba693e9127232f.png) מתקיים
מתקיים
נניח בנוסף כי 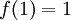 הוכח כי
הוכח כי
![\lim_{n\rightarrow\infty}\Big[\int_a^b|f(x)|^ndx\Big]^{\frac{1}{n}}=\max_{x\in [a,b]}|f(x)|](/images/math/f/a/9/fa9cc947e16c445c559b823e2f2aa5ae.png)