הבדלים בין גרסאות בדף "88-133 אינפי 2 תשעב סמסטר ב/תרגילים/תרגיל 4/פתרון"

גרסה מ־06:36, 17 במאי 2012

הפעם יש קצת יותר עבודה, אז נתחיל יותר מוקדם (:

תוכן עניינים

1 1
2 2
- 2.1 א
- 2.2 ב
- 2.3 ג
- 2.4 ד
- 2.5 ה
- 2.6 ו
3 3
4 4
5 5

1

2

א

נפצל את האינטגרל לשניים (את האמת זה סתם לצורך הפורמליות):

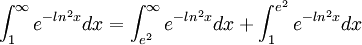
$\int_{1}^{\infty}e^{-ln^{2}x}dx=\int_{e^{2}}^{\infty}e^{-ln^{2}x}dx+\int_{1}^{e^{2}}e^{-ln^{2}x}dx$

האינטגרל השני מתכנס כי הפונקציה רציפה בקטע הסגור ולכן אינטגרבילית בו.

נבדוק את ההתכנסות של האינטגרל הראשון:

ידוע כי עבור כל 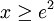$x\geq e^{2}$ מתקיים: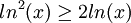 $ln^{2}(x)\geq 2ln(x)$

ומכאן שמתקיים, 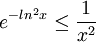$e^{-ln^{2}x}\leq \frac{1}{x^{2}}$ .

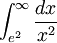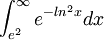ולפי מבחן ההשוואה הראשון, האינטגרל $\int_{e^{2}}^{\infty}\frac{dx}{x^{2}}$ מתכנס ולכן גם $\int_{e^{2}}^{\infty}e^{-ln^{2}x}dx$ .

הראנו ששני החלקים מתכנסים ולכן האינטגרל מתכנס.

ב

השאלה הופיעה בתרגילי בית משנים קודמות: ראו שאלה 7

ג

האינטגרל מתכנס לפי מבחן דיריכלה

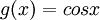$g(x)=cosx$ , הינה פונקציה רציפה והאינטגרל שלה חסום בכל קטע סופי.

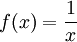$f(x)=\frac{1}{x}$ הינה פונקציה רציפה מונוטונית יורדת ששואפת ל0.

ולכן מתקיימים כל התנאים הנדרשים להפעלת המבחן.

ד

מתקיים: 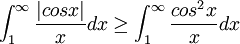$\int_{1}^{\infty}\frac{|cosx|}{x}dx\geq\int_{1}^{\infty}\frac{cos^{2}x}{x}dx$ ,

ולכן האינטגרל מתבדר לפי מבחן ההשוואה הראשון (לפי סעיף ה').

ה

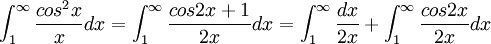
$\int_{1}^{\infty}\frac{cos^{2}x}{x}dx=\int_{1}^{\infty}\frac{cos2x+1}{2x}dx=\int_{1}^{\infty}\frac{dx}{2x}+\int_{1}^{\infty}\frac{cos2x}{2x}dx$

האינטגרל הוא סכום של אינטגרל מתבדר ואינטגרל מתכנס (לפי דיריכלה), ולכן האינטגרל מתבדר.

ו

3

4

שאלה זו (במלואה) הופיעה בתרגיל בית קודמים: ראו פתרון לתרגיל 2

5

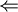נתון כי $f(x)$ פונקציה רציפה $\Leftarrow$ יש לה פונקציה קדומה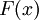 $F(x)$

לפי נוסחאת ניוטון-לייבניץ' מתקיים: 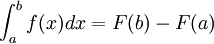$\int_{a}^{b}f(x)dx=F(b)-F(a)$

ידוע כי 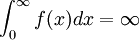$\int_{0}^{\infty}f(x)dx=\infty$ , ולכן: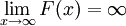 $\lim_{x \to \infty}F(x)=\infty$

לכן נוכל לכתוב את האינטגרל הלא אמיתי שאנו צריכים לחשב בצורה הבאה:

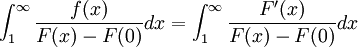
$\int_{1}^{\infty}\frac{f(x)}{F(x)-F(0)}dx=\int_{1}^{\infty}\frac{F'(x)}{F(x)-F(0)}dx$

אך לפני שנחשב את האינטגרל עלינו להסביר מדוע בכלל ניתן לדבר עליו:

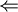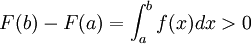$f(x)$ רציפה וחיובית $\Leftarrow$ לכל $a,b\in[0,\infty)$ מתקיים: $F(b)-F(a)=\int_{a}^{b}f(x)dx>0$ ,

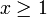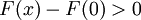ובפרט לכל $x\geq 1$ מתקיים: $F(x)-F(0)>0$ .

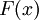$F(x)$ גזירה ולכן רציפה 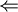$\Leftarrow$ הפונקציה 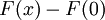$F(x)-F(0)$ רציפה וחיובית.

מכיוון ששתי הפונקציות רציפות ו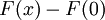 $F(x)-F(0)$ חיובית 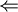$\Leftarrow$ הפונקציה 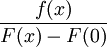$\frac{f(x)}{F(x)-F(0)}$ רציפה, ולכן אינטגרבילית על כל קטע סופי על הישר.

וכאן סיימנו להראות שניתן לדבר על האינטגרל הלא אמיתי.

כעת נוכל לחשב את האינטגרל עצמו:

לטעמי נוחות בלבד נסמן: $a:=F(1)-F(0)$

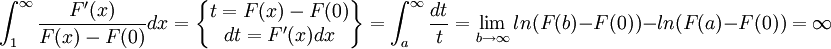
$\int_{1}^{\infty}\frac{F'(x)}{F(x)-F(0)}dx=\begin{Bmatrix} t=F(x)-F(0)\\ dt=F'(x)dx \end{Bmatrix}=\int_{a}^{\infty}\frac{dt}{t}=\lim_{b \to \infty}ln(F(b)-F(0))-ln(F(a)-F(0))=\infty$

וסיימנו (:

@@ שורה 47: / שורה 47: @@
 === ה ===
+<math>\int_{1}^{\infty}\frac{cos^{2}x}{x}dx=\int_{1}^{\infty}\frac{cos2x+1}{2x}dx=\int_{1}^{\infty}\frac{dx}{2x}+\int_{1}^{\infty}\frac{cos2x}{2x}dx</math>
+האינטגרל הוא סכום של אינטגרל מתבדר ואינטגרל מתכנס (לפי דיריכלה), ולכן האינטגרל מתבדר.
 === ו ===

הבדלים בין גרסאות בדף "88-133 אינפי 2 תשעב סמסטר ב/תרגילים/תרגיל 4/פתרון"

גרסה מ־06:36, 17 במאי 2012

תוכן עניינים

1

2

א

ב

ג

ד

ה

ו

3

4

5

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים