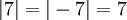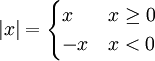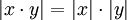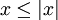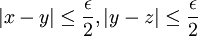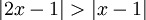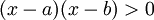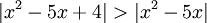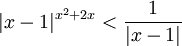הבדלים בין גרסאות בדף "מכינה למחלקת מתמטיקה/מערכי שיעור/2"
מתוך Math-Wiki
(←תרגילים) |
|||
| שורה 1: | שורה 1: | ||
| − | =ערך מוחלט= | + | =ערך מוחלט ואי שיוויונים= |
הערך המוחלט של מספר ממשי הוא האורך שלו, כלומר המרחק שלו מראשית הציר. לדוגמא: | הערך המוחלט של מספר ממשי הוא האורך שלו, כלומר המרחק שלו מראשית הציר. לדוגמא: | ||
| שורה 43: | שורה 43: | ||
**<math>|x|\leq L</math> אם ורק אם <math>-L\leq x\leq L</math> | **<math>|x|\leq L</math> אם ורק אם <math>-L\leq x\leq L</math> | ||
**<math>|x|\geq L</math> אם ורק אם <math>x\geq L</math> '''או''' <math>x\leq -L</math> | **<math>|x|\geq L</math> אם ורק אם <math>x\geq L</math> '''או''' <math>x\leq -L</math> | ||
| + | |||
| + | |||
| + | ==תכונות של אי שיוויונים== | ||
| + | |||
| + | *<math>x\leq y</math> אם ורק אם <math>-x\geq -y</math> | ||
| + | |||
| + | |||
| + | *נניח <math>0\leq x,y</math> אזי <math>x\leq y</math> אם ורק אם <math>x^2\leq y^2</math> | ||
| + | |||
| + | |||
| + | *נניח <math>0< x,y</math> אזי <math>x\leq y</math> אם ורק אם <math>\frac{1}{x} \geq \frac{1}{y}</math> | ||
| שורה 79: | שורה 90: | ||
'''תרגיל''': מצא עבור אילו ערכי x מתקיים אי השיוויון הבא: | '''תרגיל''': מצא עבור אילו ערכי x מתקיים אי השיוויון הבא: | ||
::<math>|x^2-5x+4|>|x^2-5x|</math> | ::<math>|x^2-5x+4|>|x^2-5x|</math> | ||
| + | |||
| + | |||
| + | =אי שיוויונים מעריכיים= | ||
| + | |||
| + | נניח <math>a>1</math>, אזי | ||
| + | ::<math>a^x\leq a^y</math> אם ורק אם <math>x\leq y</math> | ||
| + | |||
| + | |||
| + | '''תרגיל''': נניח כי <math>a<1</math> הוכח כי: | ||
| + | |||
| + | ::<math>a^x\leq a^y</math> אם ורק אם <math>x\geq y</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''תרגיל''': מצא לאילו ערכי x מתקיים אי השיוויון הבא: | ||
| + | |||
| + | ::<math>|x-1|^{x^2+2x} < \frac{1}{|x-1|}</math> | ||
גרסה מ־06:38, 2 באוגוסט 2012
תוכן עניינים
ערך מוחלט ואי שיוויונים
הערך המוחלט של מספר ממשי הוא האורך שלו, כלומר המרחק שלו מראשית הציר. לדוגמא:
ההגדרה המדוייקת של הערך המוחלט היא:
תכונות של הערך המוחלט
- לכל x מתקיים
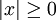
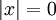 אם ורק אם
אם ורק אם 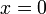
- אי שיוויון המשולש:
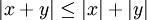
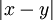 הוא המרחק בין x לבין y
הוא המרחק בין x לבין y
- נניח
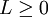 אזי
אזי
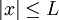 אם ורק אם
אם ורק אם 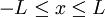
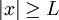 אם ורק אם
אם ורק אם 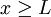 או
או 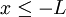
תכונות של אי שיוויונים
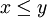 אם ורק אם
אם ורק אם 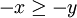
- נניח
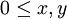 אזי
אזי 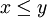 אם ורק אם
אם ורק אם 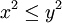
- נניח
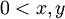 אזי
אזי 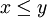 אם ורק אם
אם ורק אם 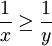
תרגילים
תרגיל: הוכח את אי שיוויון המשולש
תרגיל: הוכח כי 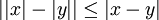
תרגיל: יהיו 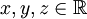 מספרים ממשיים. יהי
מספרים ממשיים. יהי 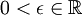 מספר ממשי חיובי. עוד נניח כי מתקיים:
מספר ממשי חיובי. עוד נניח כי מתקיים:
הוכח כי 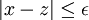
תרגיל: מצא עבור אילו ערכי x מתקיים אי השיוויון הבא:
תרגיל: מצא עבור אילו ערכי x מתקיים אי השיוויון הבא:
(חלק למקרים כאשר a=b וכאשר a שונה מ-b)
תרגיל: מצא עבור אילו ערכי x מתקיים אי השיוויון הבא:
אי שיוויונים מעריכיים
נניח 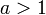 , אזי
, אזי
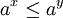 אם ורק אם
אם ורק אם 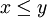
תרגיל: נניח כי 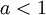 הוכח כי:
הוכח כי:
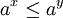 אם ורק אם
אם ורק אם 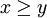
תרגיל: מצא לאילו ערכי x מתקיים אי השיוויון הבא: