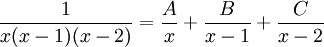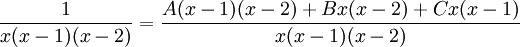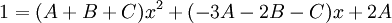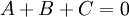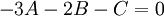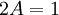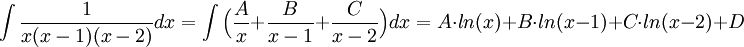הבדלים בין גרסאות בדף "מכינה למחלקת מתמטיקה/מערכי שיעור/11"
מתוך Math-Wiki
(←חילוק פולינומים) |
(←פירוק לשברים חלקיים) |
||
| שורה 71: | שורה 71: | ||
::<math>\frac{1}{x(x-1)(x-2)}=\frac{A(x-1)(x-2) +Bx(x-2) + Cx(x-1)}{x(x-1)(x-2)}</math> | ::<math>\frac{1}{x(x-1)(x-2)}=\frac{A(x-1)(x-2) +Bx(x-2) + Cx(x-1)}{x(x-1)(x-2)}</math> | ||
| + | |||
| + | |||
| + | נשווה את המונים בין שני השברים כיוון שהמכנים שווים: | ||
| + | |||
| + | |||
| + | ::<math>1 = (A+B+C)x^2 + (-3A-2B-C)x + 2A</math> | ||
| + | |||
| + | |||
| + | ולכן מהשוואת המקדמים של החזקות השונות של x מקבלים את המשוואות הבאות: | ||
| + | |||
| + | |||
| + | ::<math>A+B+C=0</math> | ||
| + | ::<math>-3A-2B-C=0</math> | ||
| + | ::<math>2A=1</math> | ||
| + | |||
| + | |||
| + | לאחר חישוב הקבועים אנו יכולים לחשב את האינטגרל. | ||
| + | |||
| + | |||
| + | ::<math>\int\frac{1}{x(x-1)(x-2)}dx=\int\Big(\frac{A}{x} + \frac{B}{x-1} + \frac{C}{x-2}\Big)dx= A\cdot ln(x) +B\cdot ln(x-1) + C\cdot ln(x-2) + D </math> | ||
גרסה מ־12:07, 23 באוגוסט 2012
פירוק פולינומים
לכל פולינום 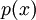 , אם
, אם 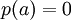 אזי הפולינום מתחלק ב
אזי הפולינום מתחלק ב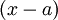
פירוק פולינום ריבועי:
לפולינומים אחרים נשתמש בנוסחאות כפל מקוצר או ננחש שורש, ואם נצליח נחלק בו.
דוגמא:
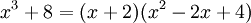
חילוק פולינומים
נביט בפולינום 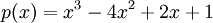 ונשים לב כי
ונשים לב כי 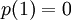 ולכן נחלק ב
ולכן נחלק ב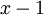
אלגוריתם לחילוק פולינומים
א. חלק את המונום הגבוה של הפולינום המחולק במונום הגבוה של הפולינום המחלק
ב. כפול את התוצאה בפולינום המחלק, וחסר מהפולינום המחולק
ג. חזור לשלב א' כאשר הפולינום המחולק הוא התוצאה מסעיף ב'. סכום חלוקות המונומים מסעיף א' הוא המנה
ביחד מתקיים: 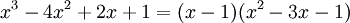
פירוק לשברים חלקיים
חשב את האינטגרל 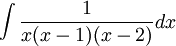
על מנת לחשב את האינטגרל נפרק לשברים חלקיים:
נבצע מכנה משותף
נשווה את המונים בין שני השברים כיוון שהמכנים שווים:
ולכן מהשוואת המקדמים של החזקות השונות של x מקבלים את המשוואות הבאות:
לאחר חישוב הקבועים אנו יכולים לחשב את האינטגרל.
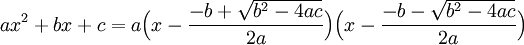
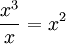
![x^3-4x^2+2x+1 - x^2[x-1]= -3x^2+2x+1](/images/math/3/e/a/3eae94cab6ea13ac94b55dbc1d9d4481.png)
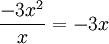
![-3x^2+2x+1 - (-3x)[x-1]= -x+1](/images/math/e/1/9/e19e67137341313f5289e890b666bfec.png)
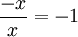
![-x+1 - (-1)[x-1] = 0](/images/math/3/4/5/345e59361394631fbaddfd95b6573271.png)