הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/29.5.11"
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
מ (←דוגמאות) |
|||
| (6 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | {{ | + | {{המשך הגיע|תיאור=משפט 3|תאריך=24.5.11}} |
=טורי חזקות {{הערה|(המשך)}}= | =טורי חזקות {{הערה|(המשך)}}= | ||
==משפט 4== | ==משפט 4== | ||
נניח שלטור <math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n</math> יש רדיוס התכנסות <math>R>0</math>, אזי: | נניח שלטור <math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n</math> יש רדיוס התכנסות <math>R>0</math>, אזי: | ||
| − | # f גזירה אינסוף פעמים בקטע <math>(x_0-R,x_0+R)</math> ולכל <math>k\in\mathbb N\cup\{0\}</math> מתקיים <math>f^{(k)}(x)=\sum_{n=k}^\infty \frac{n!}{(n-k)!}a_n(x-x_0)^{n-k}</math>. רדיוס ההתכנסות של | + | # f גזירה אינסוף פעמים בקטע <math>(x_0-R,x_0+R)</math> ולכל <math>k\in\mathbb N\cup\{0\}</math> מתקיים <math>f^{(k)}(x)=\sum_{n=k}^\infty \frac{n!}{(n-k)!}a_n(x-x_0)^{n-k}</math>. רדיוס ההתכנסות של כל אחד מהטורים הגזורים הוא R. |
# לכל <math>k\in\mathbb N\cup\{0\}</math>, <math>a_k=\frac{f^{(k)}(x_0)}{k!}</math>, ז"א הטור הוא טור טיילור של f סביב <math>x_0</math>. | # לכל <math>k\in\mathbb N\cup\{0\}</math>, <math>a_k=\frac{f^{(k)}(x_0)}{k!}</math>, ז"א הטור הוא טור טיילור של f סביב <math>x_0</math>. | ||
===הוכחה=== | ===הוכחה=== | ||
| שורה 10: | שורה 10: | ||
# הוכחנו בסעיף 1 ש-<math>f^{(k)}(x)=\sum_{n=k}^\infty \frac{n!}{(n-k)!}a_n(x-x_0)^{n-k}</math>. נציב <math>x=x_0</math> ונקבל <math>f^{(k)}(x_0)=\frac{k!}{(k-k)!}a_k+\underbrace{\frac{(k+1)!}{(k+1-k)!}a_{k+1}(x_0-x_0)}_{=0}+\dots=k!a_k</math>, כלומר <math>a_k=\frac{f^{(k)}(x_0)}{k!}</math>. {{משל}} | # הוכחנו בסעיף 1 ש-<math>f^{(k)}(x)=\sum_{n=k}^\infty \frac{n!}{(n-k)!}a_n(x-x_0)^{n-k}</math>. נציב <math>x=x_0</math> ונקבל <math>f^{(k)}(x_0)=\frac{k!}{(k-k)!}a_k+\underbrace{\frac{(k+1)!}{(k+1-k)!}a_{k+1}(x_0-x_0)}_{=0}+\dots=k!a_k</math>, כלומר <math>a_k=\frac{f^{(k)}(x_0)}{k!}</math>. {{משל}} | ||
===מסקנה {{הערה|(משפט היחידות לטורי חזקות)}}=== | ===מסקנה {{הערה|(משפט היחידות לטורי חזקות)}}=== | ||
| − | נניח ששני טורי חזקות בקטע שלם, כלומר <math>\sum_{n=0}^\infty a_n(x-x_0)^n=\sum_{n=0}^\infty b_n(x-x_0)^n</math> לכל <math>x\in(a,b)\ne\varnothing</math>, אזי <math>\forall n:\ a_n=b_n</math>. | + | נניח ששני טורי חזקות שווים זה לזה בקטע שלם, כלומר <math>\sum_{n=0}^\infty a_n(x-x_0)^n=\sum_{n=0}^\infty b_n(x-x_0)^n</math> לכל <math>x\in(a,b)\ne\varnothing</math>, אזי <math>\forall n:\ a_n=b_n</math>. |
====הוכחה==== | ====הוכחה==== | ||
נגדיר פונקציה גבולית <math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n=\sum_{n=0}^\infty b_n(x-x_0)^n</math>. | נגדיר פונקציה גבולית <math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n=\sum_{n=0}^\infty b_n(x-x_0)^n</math>. | ||
| שורה 17: | שורה 17: | ||
חשוב לא להתבלבל: יתכן בהחלט מצב בו <math>\sum_{n=0}^\infty a_n(x-x_0)^n=\sum_{n=0}^\infty b_n(x-x_1)^n</math> אבל <math>a_n\ne b_n</math> עבור n כלשהו. | חשוב לא להתבלבל: יתכן בהחלט מצב בו <math>\sum_{n=0}^\infty a_n(x-x_0)^n=\sum_{n=0}^\infty b_n(x-x_1)^n</math> אבל <math>a_n\ne b_n</math> עבור n כלשהו. | ||
==דוגמאות== | ==דוגמאות== | ||
| − | # נמצא טור מקלורין | + | # נמצא את טור מקלורין <math>\sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}x^n</math> של הפונקציה <math>f(x)=\frac1{1-x}</math>: ידוע לנו ש-<math>\frac1{1-x}=\sum_{n=0}^\infty x^n</math> עבור <math>|x|<1</math>. לפי משפט 4 טור זה הוא בהכרח טור טיילור של f סביב 0, כלומר זה טור מקלורן של f. {{משל}} |
| − | # נמצא טור טיילור של <math>f(x)=\frac1{1-x}</math> סביב <math>x_0=\frac12</math>, ז"א <math>\sum_{n=0}^\infty\frac{f^{(n)}\left(\frac12\right)}{n!}\left(x-\frac12\right)^n</math>.<br/>''דרך 1:'' {{left|<math>\begin{align}f(x)&=(1-x)^{-1}\\f'(x)&=(1-x)^{-2}\\f''(x)&=2(1-x)^{-3}\\f^{(3)}(x)&=6(1-x)^{-4}\\f^{(n)}(x)&=n!(1-x)^{-n-1}\end{align}</math>}}נציב <math>x=\frac12</math> לקבל <math>f\left(\frac12\right)=2,\ \dots,\ f^{(n)}\left(\frac12\right)=n!2^{n+1}</math> ולכן הטור הוא <math>\sum_{n=0}^\infty\frac{f^{(n)}\left(\frac12\right)}{n!}\left(x-\frac12\right)^n=\sum_{n=0}^\infty2^{n+1}\left(x-\frac12\right)^n</math>. לצערנו עדיין לא ניתן לדעת בוודאות שהטור אכן מתכנס ל-f כי לא וידאנו שהשארית שואפת ל-0.<br/>''דרך 2:'' <math>\frac1{1-x}=\frac1{\frac12-\left(x-\frac12\right)}=2\frac1{1-2\left(x-\frac12\right)}=2\sum_{n=0}^\infty\left(2\left(x-\frac12\right)\right)^n</math>. בניסיון השני קיבלנו את אותה התוצאה מהר יותר, והפעם אנו גם יודעים שהטור מתכנס ל-f כאשר <math>\left|2\left(x-\frac12\right)\right|<1</math>, כלומר כש-<math>\left|x-\frac12\right|<\frac12</math>. {{משל}}<br/>''נסכם:'' <math>\sum_{n=0}^\infty x^n=\frac1{1-x}=\sum_{n=0}^\infty 2^{n+1}\left(x-\frac12\right)^n</math> בקטע <math>(0,1)</math> ויש כאן שני טורי חזקות שונים לגמרי שמתכנסים לאותה פונקציה. זה לא סותר את משפט היחידות כי לטורים אלה יש מרכז שונה. | + | # נמצא טור טיילור של <math>f(x)=\frac1{1-x}</math> סביב <math>x_0=\frac12</math>, ז"א <math>\sum_{n=0}^\infty\frac{f^{(n)}\left(\frac12\right)}{n!}\left(x-\frac12\right)^n</math>.<br/>''דרך 1:'' {{left|<math>\begin{align}f(x)&=(1-x)^{-1}\\f'(x)&=(1-x)^{-2}\\f''(x)&=2(1-x)^{-3}\\f^{(3)}(x)&=6(1-x)^{-4}\\&\;\;\vdots\\f^{(n)}(x)&=n!(1-x)^{-n-1}\end{align}</math>}}נציב <math>x=\frac12</math> לקבל <math>f\left(\frac12\right)=2,\ \dots,\ f^{(n)}\left(\frac12\right)=n!2^{n+1}</math> ולכן הטור הוא <math>\sum_{n=0}^\infty\frac{f^{(n)}\left(\frac12\right)}{n!}\left(x-\frac12\right)^n=\sum_{n=0}^\infty2^{n+1}\left(x-\frac12\right)^n</math>. לצערנו עדיין לא ניתן לדעת בוודאות שהטור אכן מתכנס ל-f כי לא וידאנו שהשארית שואפת ל-0.<br/>''דרך 2:'' <math>\frac1{1-x}=\frac1{\frac12-\left(x-\frac12\right)}=2\frac1{1-2\left(x-\frac12\right)}=2\sum_{n=0}^\infty\left(2\left(x-\frac12\right)\right)^n</math>. בניסיון השני קיבלנו את אותה התוצאה מהר יותר, והפעם אנו גם יודעים שהטור מתכנס ל-f כאשר <math>\left|2\left(x-\frac12\right)\right|<1</math>, כלומר כש-<math>\left|x-\frac12\right|<\frac12</math>. {{משל}}<br/>''נסכם:'' <math>\sum_{n=0}^\infty x^n=\frac1{1-x}=\sum_{n=0}^\infty 2^{n+1}\left(x-\frac12\right)^n</math> בקטע <math>(0,1)</math> ויש כאן שני טורי חזקות שונים לגמרי שמתכנסים לאותה פונקציה. זה לא סותר את משפט היחידות כי לטורים אלה יש מרכז שונה. |
| − | # נמצא את טור מקלורין של <math>f(x)=\arctan(x)</math>, ונקבע את תחום ההתכנסות של הטור ל-f.<br/>''דרך 1:'' טור מקלורין הוא <math>\sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}x^n</math>, כאשר {{left|<math>\begin{align}f(x)&=\arctan(x)\\f'(x)&=\frac1{1+x^2}\\f''(x)&=\frac{-2x}{\left(1+x^2\right)^2}\end{align}</math>}}מכאן ואילך לא נעים לגזור, ולכן נוותר על הדרך הזו.<br/>''דרך 2:'' תחילה נחשב טור מקלורין לפונקציה <math>g(x)=\frac1{1+x^2}</math> ואז נוכל לקבל את הטור עבור <math>\arctan(x)</math> ע"י | + | # נמצא את טור מקלורין של <math>f(x)=\arctan(x)</math>, ונקבע את תחום ההתכנסות של הטור ל-f.<br/>''דרך 1:'' טור מקלורין הוא <math>\sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}x^n</math>, כאשר {{left|<math>\begin{align}f(x)&=\arctan(x)\\f'(x)&=\frac1{1+x^2}\\f''(x)&=\frac{-2x}{\left(1+x^2\right)^2}\end{align}</math>}}מכאן ואילך לא נעים לגזור, ולכן נוותר על הדרך הזו.<br/>''דרך 2:'' תחילה נחשב טור מקלורין לפונקציה <math>g(x)=\frac1{1+x^2}</math> ואז נוכל לקבל את הטור עבור <math>\arctan(x)</math> ע"י אינטגרציה איבר-איבר. כעת: <math>\frac1{1+x^2}=\frac1{1-\left(-x^2\right)}=\sum_{n=0}^\infty \left(-x^2\right)^n=\sum_{n=0}^\infty (-1)^nx^{2n}</math> עבור <math>\left|-x^2\right|<1</math>, ז"א <math>|x|<1</math>. עתה נעשה אינטגרציה: <math>\int\limits_0^x\frac{\mathrm dt}{1+t^2}=\sum_{n=0}^\infty\int\limits_0^x(-1)^nt^{2n}\mathrm dt</math> לכל <math>|x|<1</math>, ולכן <math>\arctan(x)=\sum_{n=0}^\infty(-1)^n\frac{x^{2n+1}}{2n+1}</math>. עפ"י משפט היחידות לטורי חזקות נסיק שזה טור מקלורין של <math>\arctan</math> בתחום <math>(-1,1)</math>. {{משל}} אם מותר להציב <math>x=1</math> אז נקבל את המשוואה היפה <math>\frac\pi4=1-\frac13+\frac15-\frac17+\dots</math>, אבל מכיוון שלא מתקיים <math>|1|<1</math> צריך להוכיח זאת (את ההוכחה ניתן בהרצאה הבאה). עם זאת, ניתן כבר עכשיו לדעת בוודאות ש-<math>\frac\pi6=\frac{\frac1\sqrt3}1-\frac{\left(\frac1\sqrt3\right)^3}3+\frac{\left(\frac1\sqrt3\right)^5}5-\frac{\left(\frac1\sqrt3\right)^7}7+\dots=\frac1\sqrt3\left(1-\frac1{3\cdot3}+\frac1{3^2\cdot5}-\frac1{3^3\cdot7}+\dots\right)</math>. |
| − | # מצאו את טור טיילור ל-<math>\ln(x)</math> סביב <math>x_0=1</math> וקבעו באיזה תחום הטור מתכנס ל-<math>\ln(x)</math>.<br/>''דרך 1:'' לפי הנוסחה לטור טיילור נקבל <math>\sum_{n=0}^\infty\frac{\ln^{(n)}(1)}(x-1)^n</math> ואז נבדוק מתי השארית <math>R_N(x)</math> שואפת ל-0.<br/>''דרך 2:'' <math>\ln(x)=\int\limits_1^x\frac{\mathrm dt}t</math> ולכן תחילה נפתח <math>\frac1x</math>: <math>\frac1x=\frac1{1-(-x+1)}=\sum_{n=0}^\infty(-1)^n(x-1)^n</math> כאשר <math>|x-1|<1</math>. כעת <math>\ln(x)=\sum_{n=0}^\infty\int\limits_1^x(-1)^n(x-1)^n\mathrm dx=\sum_{n=1}^\infty</math> בתחום <math>|x-1|<1</math>. {{משל}} עבור <math>x=2</math> לא מתקיים <math>|x-1|<1</math>, אבל אם בכל זאת ההצבה הזו נכונה אז נקבל <math>\ln(2)=1-\frac12+\frac13-\frac14+\dots</math> (בהרצאה הבאה נוכיח שזה נכון). | + | # מצאו את טור טיילור ל-<math>\ln(x)</math> סביב <math>x_0=1</math> וקבעו באיזה תחום הטור מתכנס ל-<math>\ln(x)</math>.<br/>''דרך 1:'' לפי הנוסחה לטור טיילור נקבל <math>\sum_{n=0}^\infty\frac{\ln^{(n)}(1)}{n!}(x-1)^n</math> ואז נבדוק מתי השארית <math>R_N(x)</math> שואפת ל-0 (כבר פתרנו דוגמאות אחרות בדרך זו ולכן אין טעם לעשות זאת שוב).<br/>''דרך 2:'' <math>\ln(x)=\int\limits_1^x\frac{\mathrm dt}t</math> ולכן תחילה נפתח <math>\frac1x</math>: <math>\frac1x=\frac1{1-(-x+1)}=\sum_{n=0}^\infty(-1)^n(x-1)^n</math> כאשר <math>|x-1|<1</math>. כעת <math>\ln(x)=\sum_{n=0}^\infty\int\limits_1^x(-1)^n(x-1)^n\mathrm dx=\sum_{n=1}^\infty (-1)^n\frac{(x-1)^{n+1}}{n+1}</math> בתחום <math>|x-1|<1</math>. {{משל}} עבור <math>x=2</math> לא מתקיים <math>|x-1|<1</math>, אבל אם בכל זאת ההצבה הזו נכונה אז נקבל <math>\ln(2)=1-\frac12+\frac13-\frac14+\dots</math> (בהרצאה הבאה נוכיח שזה נכון). |
| − | # {{הערה|(תרגיל ממבחן)}} נגדיר <math>f(x)=x^7e^{-x^2}</math>. מצאו <math>f^{(19)}(0)</math>: לכל <math>t\in\mathbb R</math> מתקיים <math>e^t=\sum_{n=0}^\infty \frac{t^n}{n!}</math> ונציב <math>t=-x^2</math> לקבל <math>f(x)=x^7e^{-x^2}=x^7\sum_{n=0}^\infty{\left(-x^2\right)^n}{n!}=\sum_{n=0}^\infty\frac{(-1)^n}{n!}x^{2n+7}</math>. לפי משפט 4 | + | # {{הערה|(תרגיל ממבחן)}} נגדיר <math>f(x)=x^7e^{-x^2}</math>. מצאו <math>f^{(19)}(0)</math>: לכל <math>t\in\mathbb R</math> מתקיים <math>e^t=\sum_{n=0}^\infty \frac{t^n}{n!}</math> ונציב <math>t=-x^2</math> לקבל <math>f(x)=x^7e^{-x^2}=x^7\sum_{n=0}^\infty\frac{\left(-x^2\right)^n}{n!}=\sum_{n=0}^\infty\frac{(-1)^n}{n!}x^{2n+7}</math>. לפי משפט 4 המקדם <math>a_{19}</math> של <math>x^{19}</math> מקיים <math>a_{19}=\frac{(-1)^6}{6!}=\frac{f^{(19)}(0)}{19!}</math> ולכן <math>f^{(19)}(0)=\frac{19!}{6!}</math>. {{משל}} |
==מבוא למשוואות דיפרנציאליות רגילות (מד"ר)== | ==מבוא למשוואות דיפרנציאליות רגילות (מד"ר)== | ||
| − | '''הגדרה:''' מד"ר היא משוואה המקשרת | + | '''הגדרה:''' מד"ר היא משוואה המקשרת פונקציה נעלמת, נגזרותיה העוקבות ופונקציות אחרות ידועות. |
===דוגמאות=== | ===דוגמאות=== | ||
# <math>f'(x)=\sin(x)</math> היא מד"ר, שפתרונה הוא <math>f(x)=-\cos(x)+c</math> עבור קבוע c כלשהו. | # <math>f'(x)=\sin(x)</math> היא מד"ר, שפתרונה הוא <math>f(x)=-\cos(x)+c</math> עבור קבוע c כלשהו. | ||
# גם <math>f(x)=f'(x)</math> היא מד"ר, ופתרונה <math>f(x)=ae^x</math> עבור קבוע a. | # גם <math>f(x)=f'(x)</math> היא מד"ר, ופתרונה <math>f(x)=ae^x</math> עבור קבוע a. | ||
# <math>f''(x)=-f(x)</math>. ניתן להוכיח שכל הפתרונות האפשריים הם מהצורה <math>a\sin(x)+b\cos(x)</math> עבור a,b קבועים. | # <math>f''(x)=-f(x)</math>. ניתן להוכיח שכל הפתרונות האפשריים הם מהצורה <math>a\sin(x)+b\cos(x)</math> עבור a,b קבועים. | ||
| − | # {{הערה|(דוגמה יותר קשה)}} נמצא פתרון כללי ל-<math>f''(x)-xf(x)=0</math> וגם פתרון כך ש-<math>f(0)=3\ \and\ f'(0)=-2</math>: נעיר שניתן להוכיח שהפתרון אינו פונקציה אלמנטרית ולכן אין טעם לנחש. במקום, נניח שיש פתרון מהסוג <math>f(x)=\sum_{n=0}^\infty a_nx^n</math> עם רדיוס התכנסות <math>R>0</math>. לפיכך <math>f''(x)=\sum_{n=2}^\infty n(n-1)(x-x_0)^{n-2}</math>. צריך להתקיים <math>f''(x)=xf(x)</math> ולכן <math>\sum_{n=2}^\infty n(n-1)a_nx^{n-2}=\sum_{n=0}^\infty a_nx^{n+1}</math> ולאחר הזזת אינדקסים נקבל: <math>\sum_{n=0}^\infty (n+2)(n+1)a_{n+2}x^n=\sum_{n=1}^\infty a_{n-1}x^n</math>. | + | # {{הערה|(דוגמה יותר קשה)}} נמצא פתרון כללי ל-<math>f''(x)-xf(x)=0</math> וגם פתרון כך ש-<math>f(0)=3\ \and\ f'(0)=-2</math>: נעיר שניתן להוכיח שהפתרון אינו פונקציה אלמנטרית ולכן אין טעם לנחש. במקום, נניח שיש פתרון מהסוג <math>f(x)=\sum_{n=0}^\infty a_nx^n</math> עם רדיוס התכנסות <math>R>0</math>. לפיכך <math>f''(x)=\sum_{n=2}^\infty n(n-1)a_n(x-x_0)^{n-2}</math>. צריך להתקיים <math>f''(x)=xf(x)</math> ולכן <math>\sum_{n=2}^\infty n(n-1)a_nx^{n-2}=\sum_{n=0}^\infty a_nx^{n+1}</math> ולאחר הזזת אינדקסים נקבל: <math>\sum_{n=0}^\infty (n+2)(n+1)a_{n+2}x^n=\sum_{n=1}^\infty a_{n-1}x^n</math>. {{המשך סיכום|תאריך=31.5.11}} ממשפט היחידות לטורי חזקות מתקיים <math>2a_2=0\ \and\ \forall n\ge1:\ (n+2)(n+1)a_{n+2}=a_{n-1}</math>. מכאן ש-<math>a_0,a_1</math> קבועים כלשהם, <math>a_2=0</math>, ו-<math>a_{n+2}=\frac{a_{n-1}}{(n+2)(n+1)}</math>, לכן <math>a_3=\frac{a_1}{3\cdot2},\ a_4=\frac{a_1}{4\cdot3},\ a_5=0,\ a_6=\frac{a_3}{6\cdot5}=\frac{a_0}{6\cdot5\cdot3\cdot2},\ a_7=\frac{a_1}{7\cdot6\cdot4\cdot3},\ a_8=0,\ \dots</math>. מכאן נובע ש-{{left|<math>\begin{align}f(x)&=\sum_{n=0}^\infty a_nx^n\\&=a_0+a_1x+\frac{a_1}{3\cdot2}x^3+\frac{a_1}{4\cdot3}x^4+\frac{a_0}{6\cdot5\cdot3\cdot2}x^6+\frac{a_1}{7\cdot6\cdot4\cdot3}x^7+\dots\\&=a_0\left(1+\frac{x^3}{3\cdot2}+\frac{x^5}{6\cdot5\cdot3\cdot2}+\dots\right)+a_1\left(x+\frac{x^4}{4\cdot3}+\frac{x^7}{7\cdot6\cdot4\cdot3}+\dots\right)\end{align}</math>}}נבדוק שהטורים האלה מתכנסים: בטור שמוכפל ב-<math>a_0</math>, היחס בין שני איברים עוקבים הוא <math>\left.\frac{x^{3n}}{3n(3n-1)(3n-3)(3n-4)\cdots}\right/\frac{x^{3n-3}}{(3n-3)(3n-4)\cdots}=\frac{x^3}{3n(3n-1)}</math>, ששואף ל-0, ולכן רדיוס ההתכנסות הוא (ממבחן המנה) <math>\infty</math>. באופן דומה מקבלים שרדיוס ההתכנסות של הטור המוכפל ב-<math>a_1</math> הוא <math>\infty</math> ולכן <math>f(x)</math> הנ"ל מוגדרת לכל x כך ש-<math>|x-0|<\infty</math>, כלומר <math>x\in\mathbb R</math>. לפי משפט 4 טורים אלו גזירים אינסוף פעמים ובפרט פעמיים ב-<math>\mathbb R</math>. כמו כן נעיר שניתן להוכיח שקיבלנו את הפתרון הכללי למד"ר, ולכן נותר רק לבדוק מתי <math>f(0)=3\ \and\ f'(0)=-2</math>: נזכר ש-<math>\forall n:\ a_n=\frac{f^{(n)}(x_0)}{n!}</math> ולכן <math>3=f^{(0)}(0)=0!a_0</math>, כלומר <math>a_0=3</math> וגם <math>-2=f^{(1)}(0)=1!a_1</math>, כלומר <math>a_1=-2</math>. מציבים ערכים אלו של <math>a_1,a_0</math> בפתרון הכללי שמצאנו ל-<math>f(x)</math> וסיימנו את התרגיל. {{משל}} |
גרסה אחרונה מ־14:32, 12 באוגוסט 2013
את משפט 3 לא סיימנו בשיעור הקודם ולכן השלמנו זאת ב־29.5.11. חלק זה מופיע בסיכום השיעור הקודם ולא בדף הנוכחי.
תוכן עניינים
טורי חזקות (המשך)
משפט 4
נניח שלטור 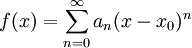 יש רדיוס התכנסות
יש רדיוס התכנסות 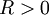 , אזי:
, אזי:
- f גזירה אינסוף פעמים בקטע
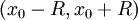 ולכל
ולכל 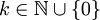 מתקיים
מתקיים 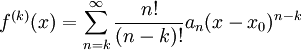 . רדיוס ההתכנסות של כל אחד מהטורים הגזורים הוא R.
. רדיוס ההתכנסות של כל אחד מהטורים הגזורים הוא R. - לכל
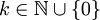 ,
, 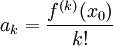 , ז"א הטור הוא טור טיילור של f סביב
, ז"א הטור הוא טור טיילור של f סביב 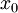 .
.
הוכחה
- באינדוקציה, בעזרת משפט 3.
- הוכחנו בסעיף 1 ש-
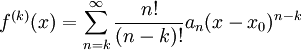 . נציב
. נציב 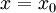 ונקבל
ונקבל 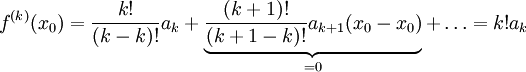 , כלומר
, כלומר 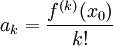 .
. 
מסקנה (משפט היחידות לטורי חזקות)
נניח ששני טורי חזקות שווים זה לזה בקטע שלם, כלומר 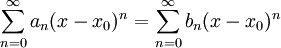 לכל
לכל 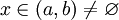 , אזי
, אזי 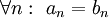 .
.
הוכחה
נגדיר פונקציה גבולית 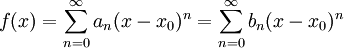 .
עפ"י סעיף 2 של משפט 4 מתקיים
.
עפ"י סעיף 2 של משפט 4 מתקיים 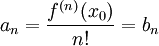 .
. 
הערה
חשוב לא להתבלבל: יתכן בהחלט מצב בו 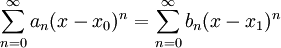 אבל
אבל 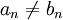 עבור n כלשהו.
עבור n כלשהו.
דוגמאות
- נמצא את טור מקלורין
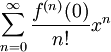 של הפונקציה
של הפונקציה 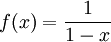 : ידוע לנו ש-
: ידוע לנו ש-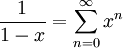 עבור
עבור 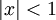 . לפי משפט 4 טור זה הוא בהכרח טור טיילור של f סביב 0, כלומר זה טור מקלורן של f.
. לפי משפט 4 טור זה הוא בהכרח טור טיילור של f סביב 0, כלומר זה טור מקלורן של f. 
- נמצא טור טיילור של
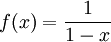 סביב
סביב 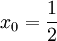 , ז"א
, ז"א 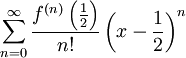 .
.
דרך 1:נציב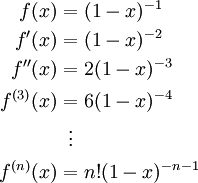
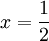 לקבל
לקבל 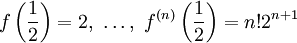 ולכן הטור הוא
ולכן הטור הוא 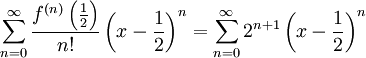 . לצערנו עדיין לא ניתן לדעת בוודאות שהטור אכן מתכנס ל-f כי לא וידאנו שהשארית שואפת ל-0.
. לצערנו עדיין לא ניתן לדעת בוודאות שהטור אכן מתכנס ל-f כי לא וידאנו שהשארית שואפת ל-0.
דרך 2: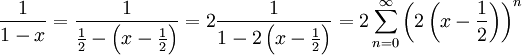 . בניסיון השני קיבלנו את אותה התוצאה מהר יותר, והפעם אנו גם יודעים שהטור מתכנס ל-f כאשר
. בניסיון השני קיבלנו את אותה התוצאה מהר יותר, והפעם אנו גם יודעים שהטור מתכנס ל-f כאשר 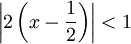 , כלומר כש-
, כלומר כש-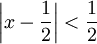 .
. 
נסכם: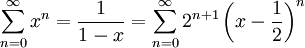 בקטע
בקטע 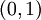 ויש כאן שני טורי חזקות שונים לגמרי שמתכנסים לאותה פונקציה. זה לא סותר את משפט היחידות כי לטורים אלה יש מרכז שונה.
ויש כאן שני טורי חזקות שונים לגמרי שמתכנסים לאותה פונקציה. זה לא סותר את משפט היחידות כי לטורים אלה יש מרכז שונה. - נמצא את טור מקלורין של
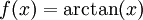 , ונקבע את תחום ההתכנסות של הטור ל-f.
, ונקבע את תחום ההתכנסות של הטור ל-f.
דרך 1: טור מקלורין הוא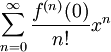 , כאשר מכאן ואילך לא נעים לגזור, ולכן נוותר על הדרך הזו.
, כאשר מכאן ואילך לא נעים לגזור, ולכן נוותר על הדרך הזו.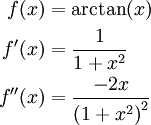
דרך 2: תחילה נחשב טור מקלורין לפונקציה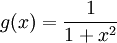 ואז נוכל לקבל את הטור עבור
ואז נוכל לקבל את הטור עבור 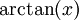 ע"י אינטגרציה איבר-איבר. כעת:
ע"י אינטגרציה איבר-איבר. כעת: 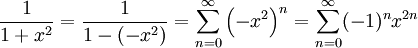 עבור
עבור 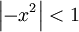 , ז"א
, ז"א 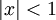 . עתה נעשה אינטגרציה:
. עתה נעשה אינטגרציה: 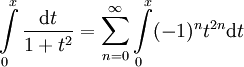 לכל
לכל 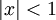 , ולכן
, ולכן 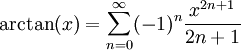 . עפ"י משפט היחידות לטורי חזקות נסיק שזה טור מקלורין של
. עפ"י משפט היחידות לטורי חזקות נסיק שזה טור מקלורין של 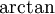 בתחום
בתחום 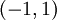 .
.  אם מותר להציב
אם מותר להציב 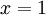 אז נקבל את המשוואה היפה
אז נקבל את המשוואה היפה 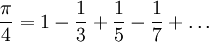 , אבל מכיוון שלא מתקיים
, אבל מכיוון שלא מתקיים 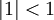 צריך להוכיח זאת (את ההוכחה ניתן בהרצאה הבאה). עם זאת, ניתן כבר עכשיו לדעת בוודאות ש-
צריך להוכיח זאת (את ההוכחה ניתן בהרצאה הבאה). עם זאת, ניתן כבר עכשיו לדעת בוודאות ש-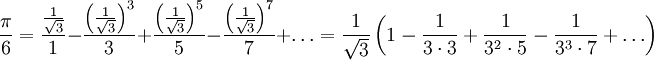 .
. - מצאו את טור טיילור ל-
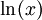 סביב
סביב 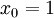 וקבעו באיזה תחום הטור מתכנס ל-
וקבעו באיזה תחום הטור מתכנס ל-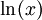 .
.
דרך 1: לפי הנוסחה לטור טיילור נקבל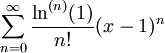 ואז נבדוק מתי השארית
ואז נבדוק מתי השארית 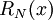 שואפת ל-0 (כבר פתרנו דוגמאות אחרות בדרך זו ולכן אין טעם לעשות זאת שוב).
שואפת ל-0 (כבר פתרנו דוגמאות אחרות בדרך זו ולכן אין טעם לעשות זאת שוב).
דרך 2: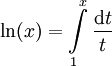 ולכן תחילה נפתח
ולכן תחילה נפתח  :
: 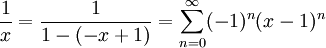 כאשר
כאשר 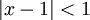 . כעת
. כעת 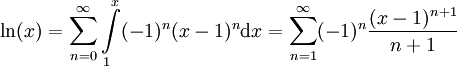 בתחום
בתחום 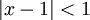 .
.  עבור
עבור 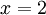 לא מתקיים
לא מתקיים 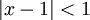 , אבל אם בכל זאת ההצבה הזו נכונה אז נקבל
, אבל אם בכל זאת ההצבה הזו נכונה אז נקבל 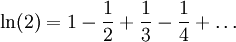 (בהרצאה הבאה נוכיח שזה נכון).
(בהרצאה הבאה נוכיח שזה נכון). - (תרגיל ממבחן) נגדיר
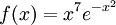 . מצאו
. מצאו 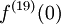 : לכל
: לכל 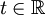 מתקיים
מתקיים 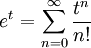 ונציב
ונציב 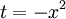 לקבל
לקבל 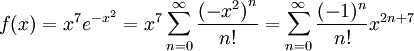 . לפי משפט 4 המקדם
. לפי משפט 4 המקדם 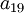 של
של 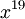 מקיים
מקיים 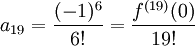 ולכן
ולכן 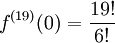 .
. 
מבוא למשוואות דיפרנציאליות רגילות (מד"ר)
הגדרה: מד"ר היא משוואה המקשרת פונקציה נעלמת, נגזרותיה העוקבות ופונקציות אחרות ידועות.
דוגמאות
-
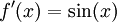 היא מד"ר, שפתרונה הוא
היא מד"ר, שפתרונה הוא 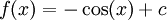 עבור קבוע c כלשהו.
עבור קבוע c כלשהו. - גם
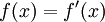 היא מד"ר, ופתרונה
היא מד"ר, ופתרונה 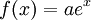 עבור קבוע a.
עבור קבוע a. -
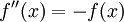 . ניתן להוכיח שכל הפתרונות האפשריים הם מהצורה
. ניתן להוכיח שכל הפתרונות האפשריים הם מהצורה 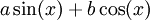 עבור a,b קבועים.
עבור a,b קבועים. - (דוגמה יותר קשה) נמצא פתרון כללי ל-
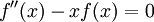 וגם פתרון כך ש-
וגם פתרון כך ש-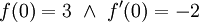 : נעיר שניתן להוכיח שהפתרון אינו פונקציה אלמנטרית ולכן אין טעם לנחש. במקום, נניח שיש פתרון מהסוג
: נעיר שניתן להוכיח שהפתרון אינו פונקציה אלמנטרית ולכן אין טעם לנחש. במקום, נניח שיש פתרון מהסוג 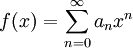 עם רדיוס התכנסות
עם רדיוס התכנסות 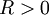 . לפיכך
. לפיכך 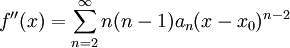 . צריך להתקיים
. צריך להתקיים 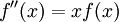 ולכן
ולכן 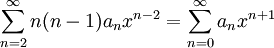 ולאחר הזזת אינדקסים נקבל:
ולאחר הזזת אינדקסים נקבל: 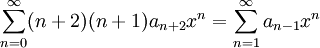 . את ההמשך עשינו בשיעור שאחריו: ממשפט היחידות לטורי חזקות מתקיים
. את ההמשך עשינו בשיעור שאחריו: ממשפט היחידות לטורי חזקות מתקיים 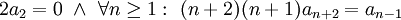 . מכאן ש-
. מכאן ש-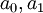 קבועים כלשהם,
קבועים כלשהם, 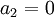 , ו-
, ו-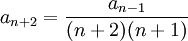 , לכן
, לכן 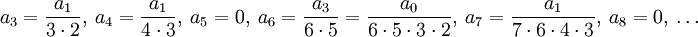 . מכאן נובע ש-נבדוק שהטורים האלה מתכנסים: בטור שמוכפל ב-
. מכאן נובע ש-נבדוק שהטורים האלה מתכנסים: בטור שמוכפל ב-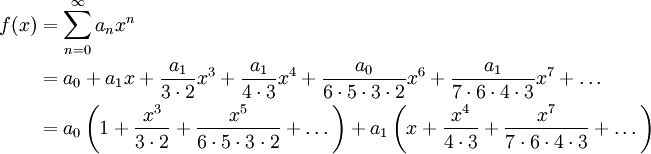
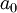 , היחס בין שני איברים עוקבים הוא
, היחס בין שני איברים עוקבים הוא 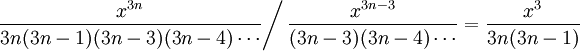 , ששואף ל-0, ולכן רדיוס ההתכנסות הוא (ממבחן המנה)
, ששואף ל-0, ולכן רדיוס ההתכנסות הוא (ממבחן המנה) 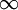 . באופן דומה מקבלים שרדיוס ההתכנסות של הטור המוכפל ב-
. באופן דומה מקבלים שרדיוס ההתכנסות של הטור המוכפל ב-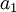 הוא
הוא 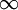 ולכן
ולכן 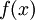 הנ"ל מוגדרת לכל x כך ש-
הנ"ל מוגדרת לכל x כך ש-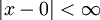 , כלומר
, כלומר 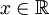 . לפי משפט 4 טורים אלו גזירים אינסוף פעמים ובפרט פעמיים ב-
. לפי משפט 4 טורים אלו גזירים אינסוף פעמים ובפרט פעמיים ב-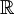 . כמו כן נעיר שניתן להוכיח שקיבלנו את הפתרון הכללי למד"ר, ולכן נותר רק לבדוק מתי
. כמו כן נעיר שניתן להוכיח שקיבלנו את הפתרון הכללי למד"ר, ולכן נותר רק לבדוק מתי 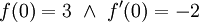 : נזכר ש-
: נזכר ש-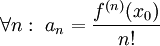 ולכן
ולכן 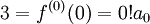 , כלומר
, כלומר 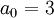 וגם
וגם 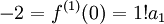 , כלומר
, כלומר 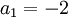 . מציבים ערכים אלו של
. מציבים ערכים אלו של 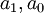 בפתרון הכללי שמצאנו ל-
בפתרון הכללי שמצאנו ל-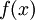 וסיימנו את התרגיל.
וסיימנו את התרגיל. 