הבדלים בין גרסאות בדף "שיחת משתמש:Nimrod"
מתוך Math-Wiki
(דף חדש: == תרגיל 1, 4.ג' == צ"ל <math>A\cap \bigcup_{i=1}^n B_i = \bigcup_{i=1}^n (A\cap B_i)</math> ואח"כ אתה משתמש בזה פעמיים (כדי להראות ש: <math>\bigc…) |
(←תרגיל 1, 2.8א: פסקה חדשה) |
||
| שורה 1: | שורה 1: | ||
== תרגיל 1, 4.ג' == | == תרגיל 1, 4.ג' == | ||
צ"ל <math>A\cap \bigcup_{i=1}^n B_i = \bigcup_{i=1}^n (A\cap B_i)</math> ואח"כ אתה משתמש בזה פעמיים (כדי להראות ש: <math>\bigcup_{i=1}^n A_i \cap \bigcup_{j=1}^m B_j' = \bigcup_{i=1}^n(A_i \cap \bigcup_{j=1}^m B_j') = \bigcup_{i=1}^n \bigcup_{j=1}^m (A_i \cap B_j')</math>). -[[משתמש:אור שחף|אור שחף]], [[שיחת משתמש:אור שחף|שיחה]], 19:01, 26 ביולי 2010 (IDT) | צ"ל <math>A\cap \bigcup_{i=1}^n B_i = \bigcup_{i=1}^n (A\cap B_i)</math> ואח"כ אתה משתמש בזה פעמיים (כדי להראות ש: <math>\bigcup_{i=1}^n A_i \cap \bigcup_{j=1}^m B_j' = \bigcup_{i=1}^n(A_i \cap \bigcup_{j=1}^m B_j') = \bigcup_{i=1}^n \bigcup_{j=1}^m (A_i \cap B_j')</math>). -[[משתמש:אור שחף|אור שחף]], [[שיחת משתמש:אור שחף|שיחה]], 19:01, 26 ביולי 2010 (IDT) | ||
| + | |||
| + | == תרגיל 1, 2.8א == | ||
| + | |||
| + | צריך להראות <math>\frac{1}{a+b\sqrt{p}} \in \mathbb{F}[\sqrt{p}]</math>. מתקיים: <math>\frac{1}{a+b\sqrt{p}} = \frac{a-b\sqrt{p}}{a^2-b^2 p}</math>. מכיוון ש-<math>a^2-b^2 p \in \mathbb{F}</math> הטענה נכונה. -[[משתמש:אור שחף|אור שחף]], [[שיחת משתמש:אור שחף|שיחה]], 18:46, 27 ביולי 2010 (IDT) | ||
גרסה מ־15:46, 27 ביולי 2010
תרגיל 1, 4.ג'
צ"ל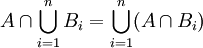 
ואח"כ אתה משתמש בזה פעמיים (כדי להראות ש: 
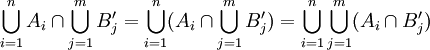). -אור שחף, שיחה, 19:01, 26 ביולי 2010 (IDT)
תרגיל 1, 2.8א
צריך להראות ![\frac{1}{a+b\sqrt{p}} \in \mathbb{F}[\sqrt{p}]](/images/math/d/d/7/dd7df529bb078476cb4e7a64580f1e5c.png)
. מתקיים: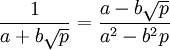 
. מכיוון ש-
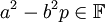הטענה נכונה. -אור שחף, שיחה, 18:46, 27 ביולי 2010 (IDT)
