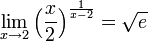הבדלים בין גרסאות בדף "Mathwiki:ארגז חול"
מתוך Math-Wiki
(←שאלה 4) |
(←שאלה 2) |
||
| שורה 7: | שורה 7: | ||
==שאלה 2== | ==שאלה 2== | ||
| + | <math>f(x)=\frac{3}{1-\sqrt{x}}-\frac{2}{1-\sqrt[3]{x}}</math> | ||
| + | <math>g(x)=ln^2(x)sin(ln(|x-1|)</math> | ||
| + | חשבו את <math>lim_{x\rightarrow 1}f(x)</math> | ||
| + | |||
| + | חשבו את <math>lim_{x\rightarrow 1}g(x)</math> | ||
| + | |||
| + | חשבו את <math>lim_{x\rightarrow 1}f(x)g(x)</math> | ||
| + | |||
| + | חשבו את <math>lim_{x\rightarrow 1}sin(f(x))</math> | ||
==שאלה 4== | ==שאלה 4== | ||
גרסה מ־18:31, 2 בינואר 2014
שאלה 1
הוכיחו לפי ההגדרה 
הוכיחו לפי ההגדרה 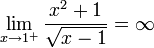
הוכיחו לפי ההגדרה 
שאלה 2
![f(x)=\frac{3}{1-\sqrt{x}}-\frac{2}{1-\sqrt[3]{x}}](/images/math/d/1/b/d1b795c7bef9fb9ca92c20556e305ac6.png)

חשבו את 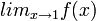
חשבו את 
חשבו את 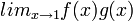
חשבו את 
שאלה 4
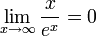
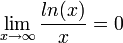
![\lim_{x\rightarrow\infty}\sqrt[x]{x}=1](/images/math/6/e/6/6e68396a1fca97ac1f3d224e67c25a80.png)