הבדלים בין גרסאות בדף "שיחה:88-113 לינארית 2 סמסטר א תשעד"
Shakedamitay (שיחה | תרומות) (←תרגיל 8 שאלה 8: פסקה חדשה) |
(←המבחן: פסקה חדשה) |
||
| (30 גרסאות ביניים של 7 משתמשים אינן מוצגות) | |||
| שורה 154: | שורה 154: | ||
תודה רבה,בתרגיל 8 שאלה ראשונה | תודה רבה,בתרגיל 8 שאלה ראשונה | ||
בהנחה ולקחתי בסיס B={(1,2,3),(0,1,0),(0,0,1)} לR3 לאחר שהרחבתי את הבסיס לU,האם מספיק לעשות גרהם-שמידט רק ל(0,1,0) ו(0,0,1) או שיש צורך לעשות גרהם שמידט לכל השלושה ולהתחיל מ(1,2,3)? | בהנחה ולקחתי בסיס B={(1,2,3),(0,1,0),(0,0,1)} לR3 לאחר שהרחבתי את הבסיס לU,האם מספיק לעשות גרהם-שמידט רק ל(0,1,0) ו(0,0,1) או שיש צורך לעשות גרהם שמידט לכל השלושה ולהתחיל מ(1,2,3)? | ||
| + | |||
| + | |||
| + | * האמת שלא חשבתי על זה. גרהם שמידט זאת גם דרך מצוינת לפתור את זה. | ||
| + | |||
| + | צריך לעשות גרהם שמידט לכל השלושה ולהתחיל מ <math>(1,2,3)</math> ואז שני הוקטורים האחרים יהיו בסיס ל <math>U^{\perp}</math>.--[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 07:48, 16 בינואר 2014 (EST) | ||
== תשובות לתרגילים 6-7 == | == תשובות לתרגילים 6-7 == | ||
| שורה 166: | שורה 171: | ||
האם יש חשיבות למכפלה הפנימית? הרי אפשר להציג את T לפי הבסיס הסטנדרטי(שהוא גם אורתונורמלי) בלי תלות במכפלה הפנימית ולקבל מטריצה צמודה לעצמה | האם יש חשיבות למכפלה הפנימית? הרי אפשר להציג את T לפי הבסיס הסטנדרטי(שהוא גם אורתונורמלי) בלי תלות במכפלה הפנימית ולקבל מטריצה צמודה לעצמה | ||
| + | |||
| + | * מצטער על העיכוב בתשובה. הבסיס הסטנדרטי הוא אורתונורמלי רק לפי המכפלה הפנימית הסטנדרטית. אם יש מכפלה פנימית אחרת, אז הצגה לפי הבסיס הסטנדרטי לא תלמד אותך כלום. | ||
| + | |||
| + | כך שוודאי שיש חשיבות למכפלה הפנימית. באופן כללי כדאי לזכור שההגדרה של <math>T^{\ast}</math> היא תלויה במכפלה פנימית. ולכל מכפלה פנימית שונה <math>T^{\ast}</math> תצא פונקציה אחרת.--[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 07:45, 16 בינואר 2014 (EST) | ||
| + | |||
| + | == שתי שאלות == | ||
| + | שתי מטריצות שיש להן פ"א אופייני שווה ופ"מ ממעלה אחת שווה (הריבוי הגיאומטרי של כל ע"ע הוא 1) דומות? | ||
| + | ועוד משהו - אם A דומה לB אפשר להגיד משהו על הדמיון בין A^2 ו- B^2? | ||
| + | |||
| + | * דבר ראשון: פולינום מינימלי ממעלה אחת זה לא אותו דבר כמו ריבוי גיאומטרי של כל ע"ע הוא 1. | ||
| + | |||
| + | למשל הפולינום המינימלי של <math>I</math> הוא <math>x-1</math> אבל הריבוי הגיאומטרי של <math>1</math> הוא <math>n</math>. | ||
| + | |||
| + | לגוף השאלה: אם הפולינום המינימלי הוא ממעלה אחת אז הוא מהצורה <math>x-c</math> כלומר המטריצה חייבת להיות סקלרית כלומר <math>cI</math> כאשר <math>c</math> הוא הע"ע היחיד. אז אם יש שתי מטריצות עם פולינום מינימלי ממעלה אחת ופ"א שווה הן ממש שוות ולא רק דומות. | ||
| + | |||
| + | משהו יותר חזק נכון: אם יש שתי מטריצות עם פולינום מינימלי שמתפרק לגורמים לינאריים (כלומר המטריצות לכסינות) ואותו פולינום אופייני אז המטריצות דומות (כי הן דומות לאותה מטריצה אלכסונית). | ||
| + | |||
| + | עוד משהו: כן. אפשר אם <math>A</math> דומה ל <math>B</math> אז <math>A^2</math> דומה ל <math>B^2</math> עם אותה מטריצת מעבר בין בסיסים. | ||
| + | |||
| + | כי אם <math>A=PBP^{-1}</math> אז <math>A^2=PBP^{-1}PBP^{-1}=PB^{2}P^{-1}</math>. | ||
| + | |||
| + | משהו יותר חזק נכון. קל לבדוק באותו אופן שאם <math>A</math> דומה ל <math>B</math> ו <math>p(x)</math> פולינום כלשהוא אז <math>p(A)</math> דומה ל <math>p(B)</math>. | ||
| + | |||
| + | השאלה שאתה שאלת זה המקרה <math>p(x)=x^2</math>. | ||
| + | |||
| + | --[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 02:25, 19 בינואר 2014 (EST) | ||
| + | |||
| + | אתה צודק... אני אהיה קצת יותר מפורט. בשאלה נתון שהפ"א של שתי המט' שווה והפ"מ שווה ל (x-4)(x-5)(x-7). החזקה של כל אחד מהגורמים הלינאריים היא 1. | ||
| + | האם אפשר להגיד שהחזקה של הפולינום המינימלי זה הבלוק המקסימלי '''לכל גורם לינארי?''', | ||
| + | כלומר ל(x-4) למשל גודל הבלוק המקסימלי הוא 1 --> הגודל הוא בדיוק 1 וכן לגבי הבלוקים האחרים ואז לשתי המט' צורת ז'ורדן | ||
| + | J1(4)+J1(5)+J1(7) | ||
| + | האם זה נכון? כי אם כן, אפשר להכליל את זה לכל מספר של גורמים לינאריים, כלומר, לכל שתי מט' שהפ"א שלהם שווה והפ"מ שווה והחזקה של כל אחד מהגורמים הלינאריים בפ"מ היא 1 אז הם דומות? | ||
| + | |||
| + | * כן. בדיוק כזה דבר היה לכם בבוחן. אם החזקה של <math>x-4</math> בפולינום המינימלי היא <math>1</math> אז זה אומר שהבלוקי ז'ורדן של <math>4</math> הם לכל היותר בגודל <math>1</math> כלומר כולם בגודל <math>1</math>. | ||
| + | |||
| + | במקרה שאתה כתבת אם הריבויים האלגבריים הם <math>a_4\quad a_5\quad a_7</math> אז הצורת ז'ורדן תהיה <math>a_4</math> פעמים את הבלוק <math>J_1(4)</math> וכו'. במילים אחרות מטריצה שהפולינום המינימלי שלה מתפרק לגורמים לינאריים היא לכסינה. | ||
| + | |||
| + | ולכן באמת שתי מטריצות עם פולינום אופייני שווה ועם פולינום מינימלי שווה '''שמתפרק לגורמים לינאריים''' הן דומות.--[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 04:29, 23 בינואר 2014 (EST) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | תודה רבה! | ||
| + | |||
| + | == מבנה המבחן == | ||
| + | |||
| + | מה יהיה מבנה המבחן ? וכמה שאלות יהיו? | ||
| + | |||
| + | * הבחינה תהיה במתכונת הבאה: חלק א' - שאלות גדולות: בחירה של 2 שאלות מתוך 3, 35 נק' כל אחת. חלק ב' - שאלות הוכח או הפרך: בחירה של 2 שאלות מתוך 3, 15 נק' כל אחת. חלק ג' - שאלת בונוס במשקל 5 נקודות. הבחינה תהיה דומה לבחינות של השנים הקודמות בקורס, עם קצת יותר דגש על הבנה על חשבון שאלות חישוביות. | ||
| + | |||
| + | == פתרונות מלאים == | ||
| + | |||
| + | תוכלו להעלות פתרונות מלאים לכל תרגילי הבית? יש עוד כמה תרגילים ללא פתרונות מלאים. | ||
| + | בנוסף, מאיזה מקורות אני יכול לתרגל? מלבד מבחנים משנים קודמות... | ||
| + | |||
| + | תודה :) | ||
| + | |||
| + | תשובה: לרוב השאלות יש פתרון. חסר רק חלק מתרגיל 7 וזה יעלה בימים הקרובים. | ||
| + | |||
| + | יש כמובן את הספר של צבאן. יש חומרים שנמצאים כאן ב math-wiki משנים קודמות. | ||
| + | |||
| + | יש ספרים טובים גם באנגלית למשל: | ||
| + | |||
| + | http://joshua.smcvt.edu/linearalgebra/ שבפרק האחרון שלו יש תרגילים טובים על דמיון מטריצות. | ||
| + | |||
| + | --[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 02:29, 3 בפברואר 2014 (EST) | ||
| + | |||
| + | == תרגיל 6 שאלות 1-3 == | ||
| + | |||
| + | בשאלות אלו נתבקשנו לבדוק האם מטריצת הגרהאם הנתונה באמת מגדירה מכפלה פנימית. לפי הפיתרונות שהועלו נבדק רק התנאי הראשון למכפלה פנימית ז"א שהמכפלה הפנימית תהיה גדולה מאפס ושווה לאפס אם ורק אם מכפלה פנימית של וקטור האפס. מה עם שאר התנאים למכפלה פנימית ? ז"א אחד וחצי לינאריות והרמיטיות ? אותם לא צריך לבדוק ולוודא שמתקיימים ? | ||
| + | |||
| + | * ברגע שמכפלה פנימית מוגדרת בצורה | ||
| + | <math><u,v>=uA\overline{v}</math> | ||
| + | אז אתה מקבל בחינם שהיא לינארית (צריך אולי לציין את זה) זה נובע בקלות מתכונות של כפל מטריצות. | ||
| + | |||
| + | הרמיטיות תתקבל אם ורק אם המטריצה הרמיטית (במקרה של <math>\mathbb{R}</math> סימטרית) שזו גם כן בדיקה מיידית - צריך רק להסתכל על המטריצה. | ||
| + | |||
| + | אולי הייתי צריך להדגיש את זה יותר בפתרון.--[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 10:30, 4 בפברואר 2014 (EST) | ||
| + | |||
| + | == אפשר לעבור על השאלות האלו בתרגול חזרה? או במקום לקבל כיוון\פתרון פה יהיה נחמד. == | ||
| + | |||
| + | http://up403.siz.co.il/up1/zw10mwgimmny.jpg | ||
| + | |||
| + | * אני אשתדל להעלות הנה תשובות לשאלות האלה במהלך היום. | ||
| + | |||
| + | אבל יש לי הצעה יותר טובה. אולי שכמה סטודנטים ייקחו על עצמם להעלות פתרונות לשאלות הלאה (כל אחד שאלה או שתיים) | ||
| + | |||
| + | חלק מהן גם פתרנו בתרגול חזרה. | ||
| + | |||
| + | מה שלא תעשו אני אשתדל להשלים. --[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 01:37, 6 בפברואר 2014 (EST) | ||
| + | |||
| + | בסוף הספקתי לכתוב תשובות. | ||
| + | |||
| + | להלן.--[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 07:18, 6 בפברואר 2014 (EST) | ||
| + | |||
| + | == <math>Ker(T^n)\cap Im(T^n)=0</math> == | ||
| + | |||
| + | שלב א': | ||
| + | |||
| + | נבחר <math>n = dim V</math> | ||
| + | |||
| + | טענת עזר: אם <math>T^{2n}(y)=0</math> אז <math>T^n(y)=0</math> | ||
| + | |||
| + | במילים אחרות: <math>Ker(T^n)=Ker(T^{2n})</math> | ||
| + | |||
| + | הוכחה: | ||
| + | |||
| + | נשים לב שיש שרשרת עולה של תתי מרחבים | ||
| + | |||
| + | <math>Ker(T)\subseteq Ker(T^2) \subseteq \cdots </math> | ||
| + | |||
| + | אבל המימד שלהם לא יכול לגדול לנצח (כי לכל היותר הוא יהיה <math>n</math>.) | ||
| + | |||
| + | ולכן קיים <math>k</math> עבורו <math>Ker(T^k)=Ker(T^{k+1})</math> | ||
| + | |||
| + | אבל אז אם <math>x\in Ker(T^{k+2})</math> אז <math>T(x)\in Ker(T^{k+1})</math> | ||
| + | |||
| + | ולכן <math>T(x) \in Ker(T^k)</math> ולכן <math>x \in Ker(T^{k+1})</math> | ||
| + | |||
| + | כלומר השויון ממשיך | ||
| + | |||
| + | ויש לנו <math>Ker(T^k)=Ker(T^{k+1})=Ker(T^{k+2})=\cdots</math> וכו'. | ||
| + | |||
| + | נסמן ב <math>k</math> את הפעם הראשונה בשרשרת שבה <math>Ker(T^k)=Ker(T^{k+1})</math> | ||
| + | |||
| + | בהכרח יתקיים <math>k\leq n </math> כי לא יכול להיות שהשרשרת גדלה יותר מ <math>n</math> פעמים. (בכל פעם שהיא גדלה, התווסף לפחות עוד 1 למימד - ובסך הכל המימד הוא <math>n</math>). | ||
| + | |||
| + | ולכן בהכרח <math>Ker(T^n)=Ker(T^{2n})</math> | ||
| + | |||
| + | שלב ב': נניח ש | ||
| + | <math>x\in Im(T^n) \cap \Ker(T^n)</math> | ||
| + | |||
| + | אז <math>T^n(x)=0</math> ו <math>T^n(y)=x</math> | ||
| + | |||
| + | כלומר <math>T^{2n}(y)=0</math> לפי שלב א' <math>x=T^n(y)=0</math> כנדרש. | ||
| + | |||
| + | --[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 07:02, 6 בפברואר 2014 (EST) | ||
| + | |||
| + | |||
| + | ==אם <math>\lambda</math> ערך עצמי יחיד ו <math>A^r=I</math> אז <math>A=\lambda I</math>== | ||
| + | |||
| + | אם <math>A^r=I</math> זה אומר ש <math>x^r-1</math> מאפס את <math>A</math>. | ||
| + | |||
| + | כלומר הפולינום המינימלי מחלק את <math>x^r-1</math>. אבל <math>x^r-1</math> מתפצל לגורמים לינאריים שונים | ||
| + | |||
| + | והפולינום המינימלי הוא מהצורה <math>(x-\lambda)^k</math> | ||
| + | ולכן <math>k=1</math> והפולינום המינימלי הוא <math>x-\lambda</math>. | ||
| + | |||
| + | נציב את <math>A</math> ונקבל ש <math>A=\lambda I</math> כנדרש | ||
| + | --[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 07:06, 6 בפברואר 2014 (EST) | ||
| + | |||
| + | ==לא קיימת T כך ש <math>T=TT^{\ast}+I</math>== | ||
| + | |||
| + | |||
| + | נניח שקיימת. אז <math>T</math> צמודה לעצמה (כי <math>TT^{\ast}+I</math> צמוד לעצמו). | ||
| + | |||
| + | ולכן כל הערכים העצמיים ממשיים (ויש ל <math>T</math> ערכים עצמיים כי היא ניתנת ללכסון). | ||
| + | |||
| + | אבל <math>T</math> מקיימת גם | ||
| + | |||
| + | <math>T=TT^\ast+I=T^2+I</math> | ||
| + | |||
| + | כלומר <math>T^2-T+I</math> | ||
| + | |||
| + | כלומר הפולינום <math>x^2-x+1</math> מאפס את <math>T</math> | ||
| + | |||
| + | אז הפולינום המינימלי צריך לחלק אותו. | ||
| + | |||
| + | אבל ל <math>TT^{\ast}+I</math> אין שורשים ממשיים. ממילא גם לפולינום המינימלי אין שורשים ממשיים. | ||
| + | |||
| + | אז ערכים עצמיים ממשיים. | ||
| + | |||
| + | בסתירה | ||
| + | |||
| + | --[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 07:12, 6 בפברואר 2014 (EST) | ||
| + | |||
| + | ==אם <math>i</math> ע"ע של <math>T</math> אז קיים <math>v</math> כך שלכל <math>u</math> מתקיים <math>v\neq T^2u+u</math>== | ||
| + | |||
| + | או בשפה של בני אדם. | ||
| + | |||
| + | <math>T^2+I</math> היא לא על. | ||
| + | |||
| + | מדובר כאן על מצב ש <math>T:V\rightarrow V</math> | ||
| + | |||
| + | ולכן <math>T</math> על אם ורק אם היא <math>הפיכה</math> | ||
| + | |||
| + | אבל <math>T^2+I=(T-iI)(T+iI)</math> | ||
| + | |||
| + | וההעתקה <math>T-iI</math> לא הפיכה כי <math>i</math> ע"ע. | ||
| + | |||
| + | ולכן גם <math>T^2+I</math> לא הפיכה. כנדרש | ||
| + | |||
| + | ==<math>Im(T^\ast)=(Ker(T))^\perp</math>== | ||
| + | |||
| + | |||
| + | ברור שזה שקול לטענה | ||
| + | |||
| + | <math>(Im(T^\ast))^\perp=(Ker(T))</math> | ||
| + | |||
| + | ואת זה נוכיח בקלות | ||
| + | |||
| + | <math>x \in Ker(T)</math> אם ורק אם <math>T(x)=0</math> | ||
| + | |||
| + | אם ורק אם <math>\forall u \quad <T(x),u>=0</math> | ||
| + | |||
| + | אם ורק אם <math>\forall u \quad <x,T^\ast(u)>=0</math> | ||
| + | |||
| + | אם ורק אם <math>x\in (Im(T^\ast))^\perp</math> | ||
| + | |||
| + | כנדרש | ||
| + | |||
| + | --[[משתמש:איתמר שטיין|איתמר שטיין]] ([[שיחת משתמש:איתמר שטיין|שיחה]]) 07:17, 6 בפברואר 2014 (EST) | ||
| + | |||
| + | == המבחן == | ||
| + | |||
| + | תוכלו בבקשה להעלות פתרונות מלאים של המבחן מועד א'? | ||
גרסה אחרונה מ־20:53, 9 במרץ 2014
תוכן עניינים
- 1 הוספת שאלה חדשה
- 2 שאלות
- 2.1 תרגיל 3
- 2.2 Kλ=K'λ
- 2.3 תרגיל 4 שאלה 2
- 2.4 שאלה אחרונה בתרגיל 5
- 2.5 מועד הגשת תרגיל 5
- 2.6 השאלה השנייה בתרגיל 5
- 2.7 העתקה נילפוטנטית
- 2.8 מבנה הבוחן
- 2.9 תרגילי בית
- 2.10 שאלה בהקשר לבוחן
- 2.11 בוחן
- 2.12 תרגיל 5
- 2.13 תרגיל 7-השאלה בין 6 ל7
- 2.14 תשובות לתרגילים 6-7
- 2.15 תרגיל 8 שאלה 8
- 2.16 שתי שאלות
- 2.17 מבנה המבחן
- 2.18 פתרונות מלאים
- 2.19 תרגיל 6 שאלות 1-3
- 2.20 אפשר לעבור על השאלות האלו בתרגול חזרה? או במקום לקבל כיוון\פתרון פה יהיה נחמד.
- 2.21
- 2.22 אם ערך עצמי יחיד ו אז
- 2.23 לא קיימת T כך ש
- 2.24 אם ע"ע של אז קיים כך שלכל מתקיים
- 2.25
- 2.26 המבחן
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
שאלות
תרגיל 3
האם קיימת מטריצה נילפותנטית לא לכסינה?והאם מטריצת האפס לכסינה באופן ריק?
- כן, בלוק ז'ורדן לעולם אינו לכסין, אך בלוק ז'ורדן עם אפסים באלכסון הוא ניליפוטנטי. כמו כן מטריצה האפס לכסינה ולא באופן ריק, אלא מתוך השיוויון
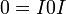 --ארז שיינר
--ארז שיינר
יותר מזה. המטריצה הנילפוטנטית היחידה שהיא לכסינה היא 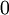 .--איתמר שטיין (שיחה) 04:32, 13 בנובמבר 2013 (EST)
.--איתמר שטיין (שיחה) 04:32, 13 בנובמבר 2013 (EST)
Kλ=K'λ
הוכחנו בכיתה ש 'K של למדא שווה לK של למדא,לפי איך שהגדרנו את 'K,לא נובע מזה שהמרחב המוכלל עבור למדא כלשהו הוא יחיד?
- תשובה: צר לי, אבל אני לא מכיר את הסימון הזה.
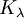 הכוונה למרחב העצמי המוכלל. איך הגדרתם את
הכוונה למרחב העצמי המוכלל. איך הגדרתם את 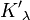 ?
?
בכל מקרה אני גם לא בטוח שהבנתי את השאלה. זה באמת נכון שעבור כל ערך עצמי יש מרחב מוכלל יחיד (הוא מוגדר בצורה מפורשת, אז ברור שהוא יחיד). --איתמר שטיין (שיחה) 03:38, 15 בנובמבר 2013 (EST)
תרגיל 4 שאלה 2
הניסוח של השאלה מאד מעורפל ודי מבלבל,למה מתכוונים בעצם בשאלה?
- הייתה באמת טעות. יובל סידר את זה.--איתמר שטיין (שיחה) 02:42, 27 בנובמבר 2013 (EST)
שאלה אחרונה בתרגיל 5
שלום,
האם התכוונתם שהמטריצה N בשאלה 8 של תרגיל 5, יכולה להיות גם מטריצת האפס?
תודה
כן. גם מטריצת האפס היא נילפוטנטית.--איתמר שטיין (שיחה) 09:30, 4 בדצמבר 2013 (EST)
מועד הגשת תרגיל 5
למתי יש להגיש את תרגיל חמש?
בינתיים עוד לא תחמנו תאריך הגשה לאף תרגיל. אני לא רואה את המדיניות הזאת משתנה בקרוב.--איתמר שטיין (שיחה) 09:31, 4 בדצמבר 2013 (EST)
השאלה השנייה בתרגיל 5
בשאלה השניה מתבקשים למצוא צורת ז'ורדן של מטריצה 5X5,כאשר פעלתי לפי האלגוריתם,בשלב השני שמוצאים בסיס למרחב העמודות של A ופותרים את המשוואה 0=(A(xC2+xC4 מקבלים את C2 לפי האלגוריתם אבל הוא תלוי לינארית במה שכבר מצאנו. כלומר מצאנו מסלול מגודל 3 והריבוי האלגברי הוא 5 איך ממשיכים מכאן?
- ראשית, לא ביקשנו למצוא בסיס מז'רדן, אלא רק את צורת ז'ורדן. ולכן במקרה הזה שזאת מטריצה קטנה יחסית לא חייבים להשתמש באלגוריתם ז'ירדון.
(אני ויובל גם עדיין לא הספקנו להראות את האלגוריתם לכיתות שלנו).
שנית, אם אתה כן רוצה להשתמש באלגוריתם, אני לא בטוח שאני מבין את הסימונים שלך אבל אני חושב שאני יכול לענות לך.גילית ש 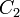 תלוי במה שכבר מצאת. כלומר שאין וקטורים חדשים שאתה יכול להוסיף כדי ליצור בסיס ל עיבוד הנוסחה נכשל (פונקציה \im לא מוכרת): \im(T)\cap \ker(T)
תלוי במה שכבר מצאת. כלומר שאין וקטורים חדשים שאתה יכול להוסיף כדי ליצור בסיס ל עיבוד הנוסחה נכשל (פונקציה \im לא מוכרת): \im(T)\cap \ker(T)
(או בסימוני מטריצות) זה אומר לך שאין מסלולים באורך 2. ואם אתה רוצה להמשיך למצוא בסיס מז'רדן אתה צריך להשלים את הבסיס של עיבוד הנוסחה נכשל (פונקציה \im לא מוכרת): \ker(T)\cap \im(T^2) שכבר יש לך לבסיס של
. וזה יוסיף לך עוד שני וקטורים שיתנו לך בסיס מז'רדן.--איתמר שטיין (שיחה) 12:39, 7 בדצמבר 2013 (EST)
העתקה נילפוטנטית
בהנחה והעתקה לינארית היא נילפוטנטית מדרגה 4,האם ייתכן איבר v כך ש(T^4(v שונה מאפס? והאם ייתכן איבר v כך שחזקה קטנה מארבע של העתקה מאפסת אותו?
- תשובה: ראשית, אני מניח שכשאתה אומר נילפוטנטית מדרגה 4 אתה מתכוון שסדר הנילפוטנטיות שלה הוא 4. ולא הדרגה במובן
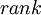 .
.
אז אם 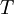 נילפוטנטית עם סדר נילפוטנטיות
נילפוטנטית עם סדר נילפוטנטיות 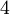 אז לכל
אז לכל 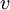 מתקיים
מתקיים 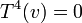 (כי
(כי 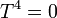 ). כמו כן, בטוח שיש איברים כך שחזקה יותר קטנה מ
). כמו כן, בטוח שיש איברים כך שחזקה יותר קטנה מ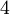 מאפסת אותם. למשל אם
מאפסת אותם. למשל אם 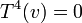 אז
אז 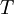 מאפס את
מאפס את 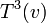 .--איתמר שטיין (שיחה) 11:46, 7 בדצמבר 2013 (EST)
.--איתמר שטיין (שיחה) 11:46, 7 בדצמבר 2013 (EST)
מבנה הבוחן
אמרתם אתמול בתירגול שיהיה היום את המבנה של הבוחן ופירוט עליו. תוכלו להעלות את זה?
- יהיו בבוחן 3 שאלות (אולי עם סעיפים). אחת מהן תהיה מתרגילי הבית.
--איתמר שטיין (שיחה) 09:42, 12 בדצמבר 2013 (EST)
תרגילי בית
האם אפשר להעלות בבקשה פתרונות מלאים לתרגילי הבית?
- חסר כרגע פתרון לתרגיל 3 ולחלק מ4. לכל השאר יש. אנחנו דואגים להשלים את זה בהקדם--איתמר שטיין (שיחה) 09:42, 12 בדצמבר 2013 (EST)
שאלה בהקשר לבוחן
למתרגלים שלום, במידע ולא הצליח בבוחן הזה האם ניתן להפוכו למגן? הבעיה שלא העלו את הפתרונות בתרגיל 3 וגם הפתרונות של תרגילים 4,5 לא ברוריים. אני וקבוצת תלמידים רחבה לא מסוגלים לתרגל אפילו את ש"ב שלנו ואנחנו חוששים להיכשל בבוחן הזה ולכן אנחנו מבקשים לתת לנו אותו כמגן למקרה הצורך כמו בלינארית 1 ששם המון אנשים השתמשו בו. אשמח לתשובה
- אני לא יכול להבטיח כרגע שהבוחן יהיה מגן.--איתמר שטיין (שיחה) 11:44, 15 בדצמבר 2013 (EST)
בוחן
איפה אפשר למצוא תרגילים להכנה לבוחן? חיפשתי כאן בחנים משנים קודמות, ומצאתי רק את הבוחן משנה שעברה. האם תוכלו לתת תרגילים נוספים?
הספר של בועז צבאן (אם כי על משפט זורדן אין שם הרבה).
פרק 5 של הספר הזה. http://joshua.smcvt.edu/linearalgebra/
--איתמר שטיין (שיחה) 11:52, 15 בדצמבר 2013 (EST)
תרגיל 5
האם תרגיל 5 נמצא בחומר לבוחן ? כי הכול שם שייך לאלגוריתם לז'ירדון שלא שייך לחומר
- תרגיל 5 בחומר לבוחן. יש שם אולי חצי שאלה שקשורה לאלגוריתם לז'ירדון.--איתמר שטיין (שיחה) 03:45, 17 בדצמבר 2013 (EST)
תרגיל 7-השאלה בין 6 ל7
יש דרך מסודרת למצוא מרחב ניצב? אם כן מהי? אם לא,מה הדרך למצוא את המרחב הניצב בשאלה זו?
- במקרה הזה קל להבין מה המרחב הניצב בלי אלגוריתם מיוחד.
אבל יש אלגוריתם למציאת המרחב הניצב ואני אכתוב אותו כאן עוד מעט.--איתמר שטיין (שיחה) 12:50, 6 בינואר 2014 (EST)
- אלגוריתם למצוא את המרחב הניצב:
נניח ש 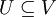 תת מרחב.
תת מרחב.
נניח ש 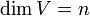 ו
ו  .
.
איך מוצאים בסיס ל  ?
?
דרך א' (תודה ליובל):
- מוצאים בסיס ל
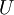 (בגודל
(בגודל 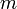 ).
). - מרחיבים אותו לבסיס עבור
 .
. - משתמשים בגרהם שמידט כדי להפוך אותו לבסיס אורתונורמלי.
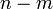 הוקטורים האחרונים יהיו בסיס ל
הוקטורים האחרונים יהיו בסיס ל  .
.
דרך ב' (תודה לי):
- בוחרים בסיס כלשהוא
 (רצוי אורתונורמלי) ומעבירים את כל הבעיה ל
(רצוי אורתונורמלי) ומעבירים את כל הבעיה ל 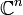 או
או 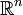 .
.
- בוחרים בסיס ל
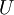 . שמים את וקטורי הבסיס בשורות מטריצה: נניח A.
. שמים את וקטורי הבסיס בשורות מטריצה: נניח A.
 הוא מרחב האפס של המטריצה
הוא מרחב האפס של המטריצה 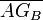 .
.
(כאשר  היא מטריצה גרהם המתאימה לבסיס שבחרנו)
היא מטריצה גרהם המתאימה לבסיס שבחרנו)
לכן כדי למצוא בסיס צריך למצוא בסיס למרחב האפס.
כמובן שאם מלכתחילה בחרנו בסיס אורתונורמלי אז 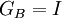 ואם זה מעל
ואם זה מעל 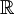 אז
אז  .
.
--איתמר שטיין (שיחה) 09:07, 7 בינואר 2014 (EST)
תודה רבה,בתרגיל 8 שאלה ראשונה בהנחה ולקחתי בסיס B={(1,2,3),(0,1,0),(0,0,1)} לR3 לאחר שהרחבתי את הבסיס לU,האם מספיק לעשות גרהם-שמידט רק ל(0,1,0) ו(0,0,1) או שיש צורך לעשות גרהם שמידט לכל השלושה ולהתחיל מ(1,2,3)?
- האמת שלא חשבתי על זה. גרהם שמידט זאת גם דרך מצוינת לפתור את זה.
צריך לעשות גרהם שמידט לכל השלושה ולהתחיל מ 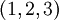 ואז שני הוקטורים האחרים יהיו בסיס ל
ואז שני הוקטורים האחרים יהיו בסיס ל  .--איתמר שטיין (שיחה) 07:48, 16 בינואר 2014 (EST)
.--איתמר שטיין (שיחה) 07:48, 16 בינואר 2014 (EST)
תשובות לתרגילים 6-7
שלום רב, לשאלות רבות של נכון\לא נכון יש אך ורק תשובות סופיות אך אין דרך פיתרון, ולכן לא ניתן ללמוד מתרגילי הבית. האם אפשר לקבל גם פיתרון מלבד תשובות סופיות ?
- נעלה בעז"ה גם תשובות מלאות.--איתמר שטיין (שיחה) 12:47, 6 בינואר 2014 (EST)
תרגיל 8 שאלה 8
האם יש חשיבות למכפלה הפנימית? הרי אפשר להציג את T לפי הבסיס הסטנדרטי(שהוא גם אורתונורמלי) בלי תלות במכפלה הפנימית ולקבל מטריצה צמודה לעצמה
- מצטער על העיכוב בתשובה. הבסיס הסטנדרטי הוא אורתונורמלי רק לפי המכפלה הפנימית הסטנדרטית. אם יש מכפלה פנימית אחרת, אז הצגה לפי הבסיס הסטנדרטי לא תלמד אותך כלום.
כך שוודאי שיש חשיבות למכפלה הפנימית. באופן כללי כדאי לזכור שההגדרה של 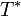 היא תלויה במכפלה פנימית. ולכל מכפלה פנימית שונה
היא תלויה במכפלה פנימית. ולכל מכפלה פנימית שונה 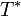 תצא פונקציה אחרת.--איתמר שטיין (שיחה) 07:45, 16 בינואר 2014 (EST)
תצא פונקציה אחרת.--איתמר שטיין (שיחה) 07:45, 16 בינואר 2014 (EST)
שתי שאלות
שתי מטריצות שיש להן פ"א אופייני שווה ופ"מ ממעלה אחת שווה (הריבוי הגיאומטרי של כל ע"ע הוא 1) דומות? ועוד משהו - אם A דומה לB אפשר להגיד משהו על הדמיון בין A^2 ו- B^2?
- דבר ראשון: פולינום מינימלי ממעלה אחת זה לא אותו דבר כמו ריבוי גיאומטרי של כל ע"ע הוא 1.
למשל הפולינום המינימלי של 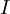 הוא
הוא 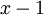 אבל הריבוי הגיאומטרי של
אבל הריבוי הגיאומטרי של 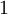 הוא
הוא  .
.
לגוף השאלה: אם הפולינום המינימלי הוא ממעלה אחת אז הוא מהצורה 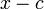 כלומר המטריצה חייבת להיות סקלרית כלומר
כלומר המטריצה חייבת להיות סקלרית כלומר 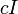 כאשר
כאשר 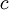 הוא הע"ע היחיד. אז אם יש שתי מטריצות עם פולינום מינימלי ממעלה אחת ופ"א שווה הן ממש שוות ולא רק דומות.
הוא הע"ע היחיד. אז אם יש שתי מטריצות עם פולינום מינימלי ממעלה אחת ופ"א שווה הן ממש שוות ולא רק דומות.
משהו יותר חזק נכון: אם יש שתי מטריצות עם פולינום מינימלי שמתפרק לגורמים לינאריים (כלומר המטריצות לכסינות) ואותו פולינום אופייני אז המטריצות דומות (כי הן דומות לאותה מטריצה אלכסונית).
עוד משהו: כן. אפשר אם  דומה ל
דומה ל  אז
אז 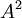 דומה ל
דומה ל 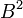 עם אותה מטריצת מעבר בין בסיסים.
עם אותה מטריצת מעבר בין בסיסים.
כי אם 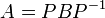 אז
אז 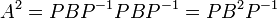 .
.
משהו יותר חזק נכון. קל לבדוק באותו אופן שאם  דומה ל
דומה ל  ו
ו 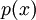 פולינום כלשהוא אז
פולינום כלשהוא אז 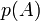 דומה ל
דומה ל 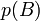 .
.
השאלה שאתה שאלת זה המקרה 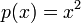 .
.
--איתמר שטיין (שיחה) 02:25, 19 בינואר 2014 (EST)
אתה צודק... אני אהיה קצת יותר מפורט. בשאלה נתון שהפ"א של שתי המט' שווה והפ"מ שווה ל (x-4)(x-5)(x-7). החזקה של כל אחד מהגורמים הלינאריים היא 1. האם אפשר להגיד שהחזקה של הפולינום המינימלי זה הבלוק המקסימלי לכל גורם לינארי?, כלומר ל(x-4) למשל גודל הבלוק המקסימלי הוא 1 --> הגודל הוא בדיוק 1 וכן לגבי הבלוקים האחרים ואז לשתי המט' צורת ז'ורדן J1(4)+J1(5)+J1(7) האם זה נכון? כי אם כן, אפשר להכליל את זה לכל מספר של גורמים לינאריים, כלומר, לכל שתי מט' שהפ"א שלהם שווה והפ"מ שווה והחזקה של כל אחד מהגורמים הלינאריים בפ"מ היא 1 אז הם דומות?
- כן. בדיוק כזה דבר היה לכם בבוחן. אם החזקה של
 בפולינום המינימלי היא
בפולינום המינימלי היא 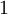 אז זה אומר שהבלוקי ז'ורדן של
אז זה אומר שהבלוקי ז'ורדן של 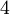 הם לכל היותר בגודל
הם לכל היותר בגודל 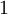 כלומר כולם בגודל
כלומר כולם בגודל 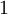 .
.
במקרה שאתה כתבת אם הריבויים האלגבריים הם 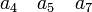 אז הצורת ז'ורדן תהיה
אז הצורת ז'ורדן תהיה 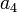 פעמים את הבלוק
פעמים את הבלוק 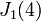 וכו'. במילים אחרות מטריצה שהפולינום המינימלי שלה מתפרק לגורמים לינאריים היא לכסינה.
וכו'. במילים אחרות מטריצה שהפולינום המינימלי שלה מתפרק לגורמים לינאריים היא לכסינה.
ולכן באמת שתי מטריצות עם פולינום אופייני שווה ועם פולינום מינימלי שווה שמתפרק לגורמים לינאריים הן דומות.--איתמר שטיין (שיחה) 04:29, 23 בינואר 2014 (EST)
תודה רבה!
מבנה המבחן
מה יהיה מבנה המבחן ? וכמה שאלות יהיו?
- הבחינה תהיה במתכונת הבאה: חלק א' - שאלות גדולות: בחירה של 2 שאלות מתוך 3, 35 נק' כל אחת. חלק ב' - שאלות הוכח או הפרך: בחירה של 2 שאלות מתוך 3, 15 נק' כל אחת. חלק ג' - שאלת בונוס במשקל 5 נקודות. הבחינה תהיה דומה לבחינות של השנים הקודמות בקורס, עם קצת יותר דגש על הבנה על חשבון שאלות חישוביות.
פתרונות מלאים
תוכלו להעלות פתרונות מלאים לכל תרגילי הבית? יש עוד כמה תרגילים ללא פתרונות מלאים. בנוסף, מאיזה מקורות אני יכול לתרגל? מלבד מבחנים משנים קודמות...
תודה :)
תשובה: לרוב השאלות יש פתרון. חסר רק חלק מתרגיל 7 וזה יעלה בימים הקרובים.
יש כמובן את הספר של צבאן. יש חומרים שנמצאים כאן ב math-wiki משנים קודמות.
יש ספרים טובים גם באנגלית למשל:
http://joshua.smcvt.edu/linearalgebra/ שבפרק האחרון שלו יש תרגילים טובים על דמיון מטריצות.
--איתמר שטיין (שיחה) 02:29, 3 בפברואר 2014 (EST)
תרגיל 6 שאלות 1-3
בשאלות אלו נתבקשנו לבדוק האם מטריצת הגרהאם הנתונה באמת מגדירה מכפלה פנימית. לפי הפיתרונות שהועלו נבדק רק התנאי הראשון למכפלה פנימית ז"א שהמכפלה הפנימית תהיה גדולה מאפס ושווה לאפס אם ורק אם מכפלה פנימית של וקטור האפס. מה עם שאר התנאים למכפלה פנימית ? ז"א אחד וחצי לינאריות והרמיטיות ? אותם לא צריך לבדוק ולוודא שמתקיימים ?
- ברגע שמכפלה פנימית מוגדרת בצורה
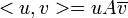 אז אתה מקבל בחינם שהיא לינארית (צריך אולי לציין את זה) זה נובע בקלות מתכונות של כפל מטריצות.
אז אתה מקבל בחינם שהיא לינארית (צריך אולי לציין את זה) זה נובע בקלות מתכונות של כפל מטריצות.
הרמיטיות תתקבל אם ורק אם המטריצה הרמיטית (במקרה של 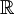 סימטרית) שזו גם כן בדיקה מיידית - צריך רק להסתכל על המטריצה.
סימטרית) שזו גם כן בדיקה מיידית - צריך רק להסתכל על המטריצה.
אולי הייתי צריך להדגיש את זה יותר בפתרון.--איתמר שטיין (שיחה) 10:30, 4 בפברואר 2014 (EST)
אפשר לעבור על השאלות האלו בתרגול חזרה? או במקום לקבל כיוון\פתרון פה יהיה נחמד.
http://up403.siz.co.il/up1/zw10mwgimmny.jpg
- אני אשתדל להעלות הנה תשובות לשאלות האלה במהלך היום.
אבל יש לי הצעה יותר טובה. אולי שכמה סטודנטים ייקחו על עצמם להעלות פתרונות לשאלות הלאה (כל אחד שאלה או שתיים)
חלק מהן גם פתרנו בתרגול חזרה.
מה שלא תעשו אני אשתדל להשלים. --איתמר שטיין (שיחה) 01:37, 6 בפברואר 2014 (EST)
בסוף הספקתי לכתוב תשובות.
להלן.--איתמר שטיין (שיחה) 07:18, 6 בפברואר 2014 (EST)
שלב א':
נבחר 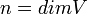
טענת עזר: אם 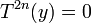 אז
אז 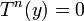
במילים אחרות: 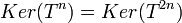
הוכחה:
נשים לב שיש שרשרת עולה של תתי מרחבים
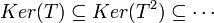
אבל המימד שלהם לא יכול לגדול לנצח (כי לכל היותר הוא יהיה  .)
.)
ולכן קיים 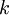 עבורו
עבורו 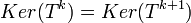
אבל אז אם  אז
אז 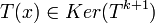
ולכן 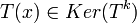 ולכן
ולכן 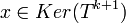
כלומר השויון ממשיך
ויש לנו 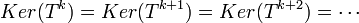 וכו'.
וכו'.
נסמן ב 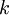 את הפעם הראשונה בשרשרת שבה
את הפעם הראשונה בשרשרת שבה 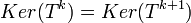
בהכרח יתקיים 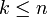 כי לא יכול להיות שהשרשרת גדלה יותר מ
כי לא יכול להיות שהשרשרת גדלה יותר מ  פעמים. (בכל פעם שהיא גדלה, התווסף לפחות עוד 1 למימד - ובסך הכל המימד הוא
פעמים. (בכל פעם שהיא גדלה, התווסף לפחות עוד 1 למימד - ובסך הכל המימד הוא  ).
).
ולכן בהכרח 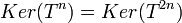
שלב ב': נניח ש עיבוד הנוסחה נכשל (פונקציה \Ker לא מוכרת): x\in Im(T^n) \cap \Ker(T^n)
אז 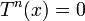 ו
ו 
כלומר 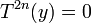 לפי שלב א'
לפי שלב א'  כנדרש.
כנדרש.
--איתמר שטיין (שיחה) 07:02, 6 בפברואר 2014 (EST)
אם  ערך עצמי יחיד ו
ערך עצמי יחיד ו 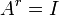 אז
אז 
אם 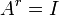 זה אומר ש
זה אומר ש 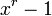 מאפס את
מאפס את  .
.
כלומר הפולינום המינימלי מחלק את 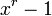 . אבל
. אבל 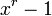 מתפצל לגורמים לינאריים שונים
מתפצל לגורמים לינאריים שונים
והפולינום המינימלי הוא מהצורה 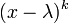 ולכן
ולכן  והפולינום המינימלי הוא
והפולינום המינימלי הוא 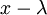 .
.
נציב את  ונקבל ש
ונקבל ש  כנדרש
--איתמר שטיין (שיחה) 07:06, 6 בפברואר 2014 (EST)
כנדרש
--איתמר שטיין (שיחה) 07:06, 6 בפברואר 2014 (EST)
לא קיימת T כך ש 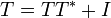
נניח שקיימת. אז 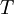 צמודה לעצמה (כי
צמודה לעצמה (כי 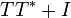 צמוד לעצמו).
צמוד לעצמו).
ולכן כל הערכים העצמיים ממשיים (ויש ל 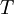 ערכים עצמיים כי היא ניתנת ללכסון).
ערכים עצמיים כי היא ניתנת ללכסון).
אבל 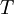 מקיימת גם
מקיימת גם

כלומר 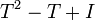
כלומר הפולינום  מאפס את
מאפס את 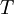
אז הפולינום המינימלי צריך לחלק אותו.
אבל ל 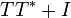 אין שורשים ממשיים. ממילא גם לפולינום המינימלי אין שורשים ממשיים.
אין שורשים ממשיים. ממילא גם לפולינום המינימלי אין שורשים ממשיים.
אז ערכים עצמיים ממשיים.
בסתירה
--איתמר שטיין (שיחה) 07:12, 6 בפברואר 2014 (EST)
אם 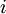 ע"ע של
ע"ע של 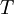 אז קיים
אז קיים 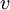 כך שלכל
כך שלכל 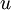 מתקיים
מתקיים 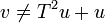
או בשפה של בני אדם.
 היא לא על.
היא לא על.
מדובר כאן על מצב ש 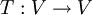
ולכן 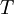 על אם ורק אם היא עיבוד הנוסחה נכשל (שגיאת לקסינג): הפיכה
על אם ורק אם היא עיבוד הנוסחה נכשל (שגיאת לקסינג): הפיכה
אבל 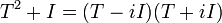
וההעתקה 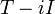 לא הפיכה כי
לא הפיכה כי 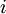 ע"ע.
ע"ע.
ולכן גם  לא הפיכה. כנדרש
לא הפיכה. כנדרש
ברור שזה שקול לטענה
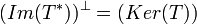
ואת זה נוכיח בקלות
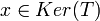 אם ורק אם
אם ורק אם 
אם ורק אם 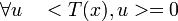
אם ורק אם 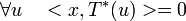
אם ורק אם 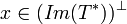
כנדרש
--איתמר שטיין (שיחה) 07:17, 6 בפברואר 2014 (EST)
המבחן
תוכלו בבקשה להעלות פתרונות מלאים של המבחן מועד א'?