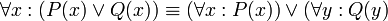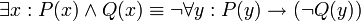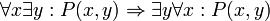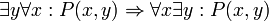הבדלים בין גרסאות בדף "Mathwiki:ארגז חול"

מתוך Math-Wiki

קפיצה אל: ניווט, חיפוש

גרסה מ־06:29, 9 באפריל 2014

חלק א'

שאלה 1

סעיף א'

הוכיחו כי $\overline{\cup A_i}=\cap \overline{A_i}$

סעיף ב'

הוכיחו/הפריכו: $(A/B)\subseteq C \iff A\subseteq C \vee B=A\cap C$

שאלה 2

סעיף א'

הוכיחו כי $A\subseteq B \iff P(A)\subseteq P(B)$

סעיף ב'

הוכיחו את תקפות הטיעון הבא:

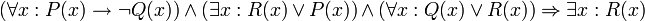
$(\forall x:P(x)\rightarrow \neg Q(x))\wedge (\exist x:R(x)\vee P(x))\wedge (\forall x:Q(x)\vee R(x)) \Rightarrow \exist x:R(x)$

שאלה 3

יהי R יחס על 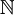$\mathbb{N}$ המוגדר ע"י

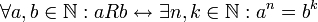
$\forall a,b\in\mathbb{N}:aRb\leftrightarrow \exist n,k\in\mathbb{N}:a^n=b^k$

סעיף א'

הוכיחו כי R יחס שקילות

סעיף ב'

מצאו את $[1]_R,[2]_R,[6]_R$

חלק ב'

שאלה 4

השלימו מספיק/הכרחי/הכרחי ומספיק/לא מספיק ולא הכרחי

על מנת שיתקיים 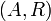$(A,R)$ קס"ה _________ שיתקיים 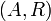$(A,R)$ קס"מ או קמ"מ
תהי 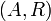$(A,R)$ קס"ח. על מנת שיתקיים $a\in A$ קטן ביותר __________ שיתקיים ש $a$ מינימלי יחיד בA
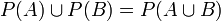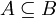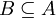
על מנת שיתקיים $P(A)\cup P(B) = P(A\cup B)$ _____________ שיתקיים $A\subseteq B$ או $B\subseteq A$
על מנת שיתקיים 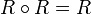$R\circ R = R$ ______________ שיתקיים שR טרנזיטיבי

שאלה 5

סעיף א'

תהי $A_n=\Big(1+\frac{(-1)^n}{2n},2+n\Big]$

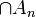
מצאו את $\cap A_n$
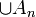
מצאו את $\cup A_n$

סעיף ב'

מצאו נוסח שקול (לוגית) לפסוק הבא, ללא שימוש בקשר השלילה:

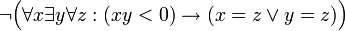
$\neg\Big(\forall x\exist y\forall z:(xy<0)\rightarrow(x=z \vee y=z)\Big)$

שאלה 6

סעיף א'

מצאו את צורת הDNF השלימה של הפסוק $(r\uparrow p)\rightarrow (q\downarrow p)$

סעיף ב'

ציירו את דיאגרמת הסה עבור יחס ההכלה על 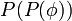$P(P(\phi))$

שאלה 7

נביט ביחס 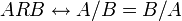$ARB \leftrightarrow A/B=B/A$

סמנו נכון/לא נכון:

R רפלקסיבי
R סימטרי
R אנטי סימטרי
R טרנזיטיבי

שאלה 8

סמנו נכון/לא נכון

$\forall x:(P(x)\vee Q(x)) \equiv (\forall x:P(x))\vee (\forall y:Q(y)$

$\exist x: P(x)\wedge Q(x) \equiv \neg \forall y: P(y)\rightarrow (\neg Q(y))$

$\forall x \exist y:P(x,y) \Rightarrow \exist y \forall x:P(x,y)$

$\exist y \forall x:P(x,y) \Rightarrow \forall x \exist y:P(x,y)$

סתם

שם מוצג למשתמש

שם מוצג למשתמש

מקור: https://math-wiki.com/index.php?title=Mathwiki:ארגז_חול&oldid=41121