הבדלים בין גרסאות בדף "88-236 אינפי 4 תשעד סמסטר ב"
עופר בוסאני (שיחה | תרומות) (←הודעות) |
|||
| (18 גרסאות ביניים של 3 משתמשים אינן מוצגות) | |||
| שורה 3: | שורה 3: | ||
==קישורים== | ==קישורים== | ||
| − | *[[שיחה:88-236 אינפי 4 | + | *[[שיחה:88-236 אינפי 4 תשעה סמסטר ב|שאלות ותשובות]] |
| − | *[ | + | *[https://www.dropbox.com/sh/l2ft3vjqeghivn5/AAD-L4yQQdwMnoarUST-KzGca סיכומים של דביר] |
*[[88-236 אינפי 4 תשעד סמסטר ב/תרגילים|תרגילים]] | *[[88-236 אינפי 4 תשעד סמסטר ב/תרגילים|תרגילים]] | ||
| שורה 14: | שורה 14: | ||
==הודעות== | ==הודעות== | ||
| + | |||
| + | ציוני בוחן [[מדיה:bohan882362014.xlsx|ציוני בוחן]] | ||
| + | |||
העלתי לכם את התרגולים 2-5. פסח שמח! --[[משתמש:עופר בוסאני|עופר בוסאני]] ([[שיחת משתמש:עופר בוסאני|שיחה]]) 08:16, 6 באפריל 2014 (EDT) | העלתי לכם את התרגולים 2-5. פסח שמח! --[[משתמש:עופר בוסאני|עופר בוסאני]] ([[שיחת משתמש:עופר בוסאני|שיחה]]) 08:16, 6 באפריל 2014 (EDT) | ||
| שורה 22: | שורה 25: | ||
הועלו פתרונות 2-5 ומבחנים של שנה שעברה. --[[משתמש:עופר בוסאני|עופר בוסאני]] ([[שיחת משתמש:עופר בוסאני|שיחה]]) 05:54, 28 במאי 2014 (EDT) | הועלו פתרונות 2-5 ומבחנים של שנה שעברה. --[[משתמש:עופר בוסאני|עופר בוסאני]] ([[שיחת משתמש:עופר בוסאני|שיחה]]) 05:54, 28 במאי 2014 (EDT) | ||
| − | לגבי השאלה היום בתרגול על ה pull back. אם יש לכם פרמטריזציה <math>(u_1,u_2,...,u_k)\rightarrow(\phi^1,...,\phi^n)</math> ונתונה לכם התבנית <math>\omega=\alpha(x_1,...,x_n)dx_{i_1}\wedge dx_{i_2},...,\wedge dx_{i_k}</math> כאשר <math>1 \leq i_r \leq k</math> אז ה pull back יהיה <math>\phi*\omega=\alpha(\phi^1(u_1,..,u_k),...,\phi^k(u_1,..,u_k))det(A)du_1,...,du_k</math> | + | לגבי השאלה היום בתרגול על ה pull back. אם יש לכם פרמטריזציה <math>(u_1,u_2,...,u_k)\rightarrow(\phi^1,...,\phi^n)</math> ונתונה לכם התבנית <math>\omega=\alpha(x_1,...,x_n)dx_{i_1}\wedge dx_{i_2},...,\wedge dx_{i_k}</math> כאשר <math>1 \leq i_r \leq k</math> אז ה pull back יהיה <math>\phi*\omega=\alpha(\phi^1(u_1,..,u_k),...,\phi^k(u_1,..,u_k))det(A)du_1\wedge,...,\wedge du_k</math> |
| + | |||
| + | לגבי תרגיל בית 3 שאלה 1 סעיף ג'. הוקטור המשיק ליריעה ברביע החיובי הינו <math>\gamma'(t)=(1,-\frac{3}{t^2})</math> ולכן אנו רוצים ש <math>arctan(-\frac{3}{t^2})=-\frac{\pi}{4}</math> הפתרון המתאים הוא <math>t=\sqrt{3}</math> --[[משתמש:עופר בוסאני|עופר בוסאני]] ([[שיחת משתמש:עופר בוסאני|שיחה]]) 08:43, 1 ביוני 2014 (EDT) | ||
| + | |||
| + | לגבי תרגיל 2 שאלה 4 סעיפים ב וג : יש לנו חיתוך של מישור עם ספירה שקובע לנו את היריעה שלנו. ישנן 3 אפשרויות: | ||
| + | |||
| + | 1) החיתוך בין המישור לספירה הינו ריק : זה קורה כאשר המישור נמצא מתחת או מעל לספירה. | ||
| + | 2) החיתוך בין המישור לספירה הינו נקודה בודדת: מצב זה יתכן רק אם הוקטורים <math>(1,1,1)</math> ו <math>(2x,2y,2z)</math> הינם תלויים לינארית שכן הוקטור <math>(1,1,1)</math> הינו מאונך למישור והוקטור <math>(2x,2y,2z)</math> הינו בכיוון הרדיאלי לספירה. מכאן שכאשר שני הוקטורים הינם תלויים המישור משיק למעגל והיריעה הינה נקודה. זה קורה כאשר (בדומה לתרגיל כיתה) <math>x=y=z</math> ואז <math>3x^2=9</math> כלומר <math>x=y=z=+-\sqrt{3}</math>. נציב במשוואה השניה ונקבל <math>+-3\sqrt{3}=a</math>. | ||
| + | 3) המישור חותך את הספירה ויוצר מעגל: כאשר a שואף לאינסוף המישור יתרחק מהספירה ונקבל חיתוך ריק, לעומת זאת בין <math>-3\sqrt{3}</math> ל <math>3\sqrt{3}</math> נקבל חיתוך שאינו ריק והוקטורים המאונכים למישור ולמעגל יהיו בת"ל - כלומר נקבל יריעה מממד 2. | ||
| + | |||
| + | לגבי תרגיל 1 שאלה א צריך למצוא הצגה עבור פונקציות מולטילינאריות מתחלפות כמובן. --[[משתמש:עופר בוסאני|עופר בוסאני]] ([[שיחת משתמש:עופר בוסאני|שיחה]]) 08:51, 5 ביוני 2014 (EDT) | ||
| + | |||
| + | לגבי הבוחן, | ||
| + | |||
| + | 1) הבוחן מורכב מ 3 שאלות. אורך הבוחן שעה. אין בחירה בשאלות. | ||
| + | |||
| + | 2) הבוחן איננו מגן ומשקלו 10%. | ||
| + | |||
| + | 3)החומר לבוחן הינו החומר של תרגילי בית 1-5. --[[משתמש:עופר בוסאני|עופר בוסאני]] ([[שיחת משתמש:עופר בוסאני|שיחה]]) 08:52, 5 ביוני 2014 (EDT) | ||
| + | |||
| + | לגבי תרגיל 5 שאלה אחרונה. בקוטב הצפוני של הכדור הפרמטריזציה <math>(\phi,\theta)\rightarrow (sin\phi cos\theta,sin\phi sin \theta, cos\phi)</math> לא מגדירה אוריינטציה שכן ההעתקה שם איננה חד חד ערכית והנגדרת לפי <math>\theta</math> מתאפסת ואין לנו בסיס למישור המשיק. למרות זאת הספירה עדיין אוריינטבילית. כלומר ניתן להגדיר בסיס עבור הקוטב הצפוני באופן רציף על הכדור. | ||
| + | |||
| + | לגבי החבר'ה שלא נבחנו באישור. לא תהיה עבודה ותוגשו על 100. | ||
| + | |||
| + | תוכלו למצוא את ציוני הבחנים [[מדיה:Quiz grades.pdf|כאן]] --[[משתמש:עופר בוסאני|עופר בוסאני]] ([[שיחת משתמש:עופר בוסאני|שיחה]]) 09:42, 8 ביולי 2014 (EDT) | ||
| − | + | הבחנים הבדוקים יהיו בחדר צילום. --[[משתמש:עופר בוסאני|עופר בוסאני]] ([[שיחת משתמש:עופר בוסאני|שיחה]]) 09:45, 8 ביולי 2014 (EDT) | |
גרסה אחרונה מ־15:06, 10 במרץ 2015
קישורים
הודעות
ציוני בוחן ציוני בוחן
העלתי לכם את התרגולים 2-5. פסח שמח! --עופר בוסאני (שיחה) 08:16, 6 באפריל 2014 (EDT)
הועלו תרגילים 4-5 --עופר בוסאני (שיחה) 09:14, 20 במאי 2014 (EDT)
הועלו מבחנים של תשע"ב. --עופר בוסאני (שיחה) 09:23, 20 במאי 2014 (EDT)
הועלו פתרונות 2-5 ומבחנים של שנה שעברה. --עופר בוסאני (שיחה) 05:54, 28 במאי 2014 (EDT)
לגבי השאלה היום בתרגול על ה pull back. אם יש לכם פרמטריזציה 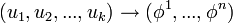 ונתונה לכם התבנית
ונתונה לכם התבנית 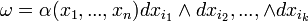 כאשר
כאשר 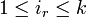 אז ה pull back יהיה
אז ה pull back יהיה 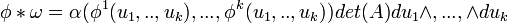
לגבי תרגיל בית 3 שאלה 1 סעיף ג'. הוקטור המשיק ליריעה ברביע החיובי הינו 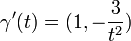 ולכן אנו רוצים ש
ולכן אנו רוצים ש 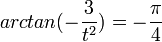 הפתרון המתאים הוא
הפתרון המתאים הוא 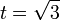 --עופר בוסאני (שיחה) 08:43, 1 ביוני 2014 (EDT)
--עופר בוסאני (שיחה) 08:43, 1 ביוני 2014 (EDT)
לגבי תרגיל 2 שאלה 4 סעיפים ב וג : יש לנו חיתוך של מישור עם ספירה שקובע לנו את היריעה שלנו. ישנן 3 אפשרויות:
1) החיתוך בין המישור לספירה הינו ריק : זה קורה כאשר המישור נמצא מתחת או מעל לספירה.
2) החיתוך בין המישור לספירה הינו נקודה בודדת: מצב זה יתכן רק אם הוקטורים 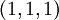 ו
ו 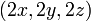 הינם תלויים לינארית שכן הוקטור
הינם תלויים לינארית שכן הוקטור 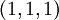 הינו מאונך למישור והוקטור
הינו מאונך למישור והוקטור 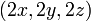 הינו בכיוון הרדיאלי לספירה. מכאן שכאשר שני הוקטורים הינם תלויים המישור משיק למעגל והיריעה הינה נקודה. זה קורה כאשר (בדומה לתרגיל כיתה)
הינו בכיוון הרדיאלי לספירה. מכאן שכאשר שני הוקטורים הינם תלויים המישור משיק למעגל והיריעה הינה נקודה. זה קורה כאשר (בדומה לתרגיל כיתה) 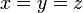 ואז
ואז 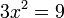 כלומר
כלומר 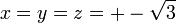 . נציב במשוואה השניה ונקבל
. נציב במשוואה השניה ונקבל 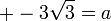 .
3) המישור חותך את הספירה ויוצר מעגל: כאשר a שואף לאינסוף המישור יתרחק מהספירה ונקבל חיתוך ריק, לעומת זאת בין
.
3) המישור חותך את הספירה ויוצר מעגל: כאשר a שואף לאינסוף המישור יתרחק מהספירה ונקבל חיתוך ריק, לעומת זאת בין 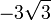 ל
ל 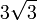 נקבל חיתוך שאינו ריק והוקטורים המאונכים למישור ולמעגל יהיו בת"ל - כלומר נקבל יריעה מממד 2.
נקבל חיתוך שאינו ריק והוקטורים המאונכים למישור ולמעגל יהיו בת"ל - כלומר נקבל יריעה מממד 2.
לגבי תרגיל 1 שאלה א צריך למצוא הצגה עבור פונקציות מולטילינאריות מתחלפות כמובן. --עופר בוסאני (שיחה) 08:51, 5 ביוני 2014 (EDT)
לגבי הבוחן,
1) הבוחן מורכב מ 3 שאלות. אורך הבוחן שעה. אין בחירה בשאלות.
2) הבוחן איננו מגן ומשקלו 10%.
3)החומר לבוחן הינו החומר של תרגילי בית 1-5. --עופר בוסאני (שיחה) 08:52, 5 ביוני 2014 (EDT)
לגבי תרגיל 5 שאלה אחרונה. בקוטב הצפוני של הכדור הפרמטריזציה 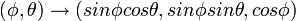 לא מגדירה אוריינטציה שכן ההעתקה שם איננה חד חד ערכית והנגדרת לפי
לא מגדירה אוריינטציה שכן ההעתקה שם איננה חד חד ערכית והנגדרת לפי 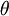 מתאפסת ואין לנו בסיס למישור המשיק. למרות זאת הספירה עדיין אוריינטבילית. כלומר ניתן להגדיר בסיס עבור הקוטב הצפוני באופן רציף על הכדור.
מתאפסת ואין לנו בסיס למישור המשיק. למרות זאת הספירה עדיין אוריינטבילית. כלומר ניתן להגדיר בסיס עבור הקוטב הצפוני באופן רציף על הכדור.
לגבי החבר'ה שלא נבחנו באישור. לא תהיה עבודה ותוגשו על 100.
תוכלו למצוא את ציוני הבחנים כאן --עופר בוסאני (שיחה) 09:42, 8 ביולי 2014 (EDT)
הבחנים הבדוקים יהיו בחדר צילום. --עופר בוסאני (שיחה) 09:45, 8 ביולי 2014 (EDT)