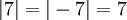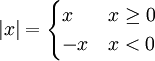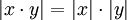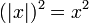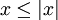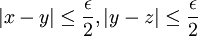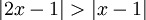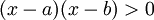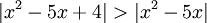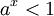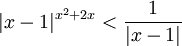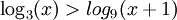הבדלים בין גרסאות בדף "מכינה למחלקת מתמטיקה/מערכי שיעור/2"
(←תכונות של הערך המוחלט) |
|||
| (5 גרסאות ביניים של משתמש אחר אחד אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | [[מכינה למחלקת מתמטיקה/מערכי שיעור|חזרה למערכי השיעור]] | ||
| + | |||
=ערך מוחלט ואי שיוויונים= | =ערך מוחלט ואי שיוויונים= | ||
| שורה 22: | שורה 24: | ||
*<math>|x\cdot y| = |x|\cdot |y|</math> | *<math>|x\cdot y| = |x|\cdot |y|</math> | ||
| + | |||
| + | *<math>(|x|)^2=x^2</math> | ||
| שורה 43: | שורה 47: | ||
**<math>|x|\leq L</math> אם ורק אם <math>-L\leq x\leq L</math> | **<math>|x|\leq L</math> אם ורק אם <math>-L\leq x\leq L</math> | ||
**<math>|x|\geq L</math> אם ורק אם <math>x\geq L</math> '''או''' <math>x\leq -L</math> | **<math>|x|\geq L</math> אם ורק אם <math>x\geq L</math> '''או''' <math>x\leq -L</math> | ||
| − | |||
==תכונות של אי שיוויונים== | ==תכונות של אי שיוויונים== | ||
| שורה 85: | שורה 88: | ||
(חלק למקרים כאשר a=b וכאשר a שונה מ-b) | (חלק למקרים כאשר a=b וכאשר a שונה מ-b) | ||
| + | |||
| + | |||
| + | '''תרגיל''': נגדיר פונקציה f כך שאם n זוגי אזי <math>f(n)=2n</math> ואם n אינו זוגי אזי <math>f(n)=\frac{n}{2}</math> | ||
| + | |||
| + | האם יש פתרון למשוואה <math>f(n)=7</math>? | ||
| שורה 90: | שורה 98: | ||
'''תרגיל''': מצא עבור אילו ערכי x מתקיים אי השיוויון הבא: | '''תרגיל''': מצא עבור אילו ערכי x מתקיים אי השיוויון הבא: | ||
::<math>|x^2-5x+4|>|x^2-5x|</math> | ::<math>|x^2-5x+4|>|x^2-5x|</math> | ||
| − | |||
=אי שיוויונים מעריכיים= | =אי שיוויונים מעריכיים= | ||
| שורה 102: | שורה 109: | ||
::<math>a^x\leq a^y</math> אם ורק אם <math>x\geq y</math> | ::<math>a^x\leq a^y</math> אם ורק אם <math>x\geq y</math> | ||
| + | |||
| + | |||
| + | '''תרגיל''': מצא לאילו ערכים של <math>a,x</math> מתקיים אי השיוויון הבא: | ||
| + | ::<math>a^x<1</math> | ||
| שורה 107: | שורה 118: | ||
::<math>|x-1|^{x^2+2x} < \frac{1}{|x-1|}</math> | ::<math>|x-1|^{x^2+2x} < \frac{1}{|x-1|}</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''תרגיל''': הראה כי | ||
| + | |||
| + | אם <math>a>1</math> אזי | ||
| + | ::<math>\log_a(x)\leq\log_a(y)</math> אם ורק אם <math>0<x\leq y</math> | ||
| + | |||
| + | |||
| + | ואם <math>a<1</math> אזי | ||
| + | ::<math>\log_a(x)\leq\log_a(y)</math> אם ורק אם <math>0<y\leq x</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''תרגיל''': מצא עבור אילו ערכי x מתקיים אי השיוויון הבא: | ||
| + | |||
| + | ::<math>\log_3(x)>log_9(x+1)</math> | ||
גרסה אחרונה מ־10:49, 29 ביוני 2015
תוכן עניינים
ערך מוחלט ואי שיוויונים
הערך המוחלט של מספר ממשי הוא האורך שלו, כלומר המרחק שלו מראשית הציר. לדוגמא:
ההגדרה המדוייקת של הערך המוחלט היא:
תכונות של הערך המוחלט
- לכל x מתקיים
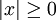
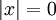 אם ורק אם
אם ורק אם 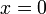
- אי שיוויון המשולש:
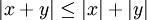
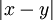 הוא המרחק בין x לבין y
הוא המרחק בין x לבין y
- נניח
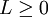 אזי
אזי
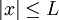 אם ורק אם
אם ורק אם 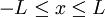
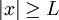 אם ורק אם
אם ורק אם 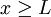 או
או 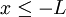
תכונות של אי שיוויונים
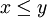 אם ורק אם
אם ורק אם 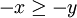
- נניח
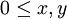 אזי
אזי 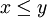 אם ורק אם
אם ורק אם 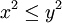
- נניח
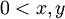 אזי
אזי 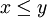 אם ורק אם
אם ורק אם 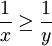
תרגילים
תרגיל: הוכח את אי שיוויון המשולש
תרגיל: הוכח כי 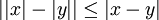
תרגיל: יהיו 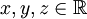 מספרים ממשיים. יהי
מספרים ממשיים. יהי 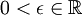 מספר ממשי חיובי. עוד נניח כי מתקיים:
מספר ממשי חיובי. עוד נניח כי מתקיים:
הוכח כי 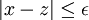
תרגיל: מצא עבור אילו ערכי x מתקיים אי השיוויון הבא:
תרגיל: מצא עבור אילו ערכי x מתקיים אי השיוויון הבא:
(חלק למקרים כאשר a=b וכאשר a שונה מ-b)
תרגיל: נגדיר פונקציה f כך שאם n זוגי אזי 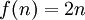 ואם n אינו זוגי אזי
ואם n אינו זוגי אזי 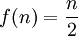
האם יש פתרון למשוואה 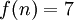 ?
?
תרגיל: מצא עבור אילו ערכי x מתקיים אי השיוויון הבא:
אי שיוויונים מעריכיים
נניח 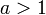 , אזי
, אזי
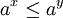 אם ורק אם
אם ורק אם 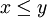
תרגיל: נניח כי 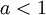 הוכח כי:
הוכח כי:
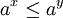 אם ורק אם
אם ורק אם 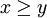
תרגיל: מצא לאילו ערכים של 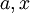 מתקיים אי השיוויון הבא:
מתקיים אי השיוויון הבא:
תרגיל: מצא לאילו ערכי x מתקיים אי השיוויון הבא:
תרגיל: הראה כי
אם 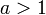 אזי
אזי
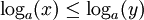 אם ורק אם
אם ורק אם 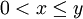
ואם 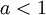 אזי
אזי
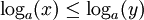 אם ורק אם
אם ורק אם 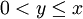
תרגיל: מצא עבור אילו ערכי x מתקיים אי השיוויון הבא: