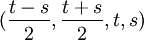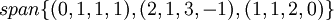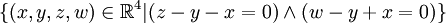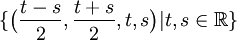הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/5"
(←בסיס ומימד) |
(←משפט המימדים) |
||
| שורה 597: | שורה 597: | ||
יש שני משתנים תלויים- x,y ושני משתנים חופשיים- z,w. נסמן z=t, w=s ונקבל פתרון כללי מהצורה <math>\big(\frac{t-s}{2},\frac{t+s}{2},t,s\big)</math> | יש שני משתנים תלויים- x,y ושני משתנים חופשיים- z,w. נסמן z=t, w=s ונקבל פתרון כללי מהצורה <math>\big(\frac{t-s}{2},\frac{t+s}{2},t,s\big)</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
גרסה מ־18:47, 12 ביולי 2015
צירופים לינאריים והמרחב הנפרש (span)
הגדרה: יהיה  מרחב וקטורי מעל
מרחב וקטורי מעל  . יהיו
. יהיו 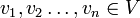 ו
ו 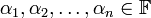 אזי ביטוי מהצורה
אזי ביטוי מהצורה 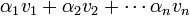 נקרא צירוף לינארי (צ"ל) של
נקרא צירוף לינארי (צ"ל) של 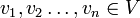 .
.
לדוגמא: 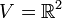 מעל
מעל 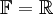 . אזי
. אזי
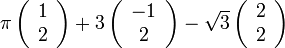
הוא צירוף לינארי.
הגדרה: המרחב הנפרש על ידי הוקטורים 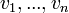 מוגדר להיות קבוצת (אוסף) כל הצירופים הלינאריים של הוקטורים הללו. כלומר,
מוגדר להיות קבוצת (אוסף) כל הצירופים הלינאריים של הוקטורים הללו. כלומר,
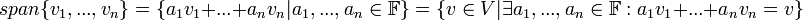 .
.
באופן כללי: תהא 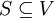 תת קבוצה של מ"ו (ייתכן קבוצה אין סופית) אזי
תת קבוצה של מ"ו (ייתכן קבוצה אין סופית) אזי
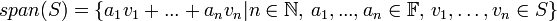
באופן שקול 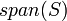 הוא איחוד כל הצירופים הלינאריים של כל תתי הקבוצות הסופיות של
הוא איחוד כל הצירופים הלינאריים של כל תתי הקבוצות הסופיות של  .
.
הערה:
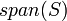 הינו תמיד תת-מרחב כפי שקל להוכיח באמצעות הקריטריון המקוצר - צירוף לינארי של צירופים לינאריים הינו צירוף לינארי בעצמו. בנוסף הוא התת מרחבב הקטן ביותר (מינימום לפי יחס ההכלה) המכיל את הקבוצה אותה הוא פורש
הינו תמיד תת-מרחב כפי שקל להוכיח באמצעות הקריטריון המקוצר - צירוף לינארי של צירופים לינאריים הינו צירוף לינארי בעצמו. בנוסף הוא התת מרחבב הקטן ביותר (מינימום לפי יחס ההכלה) המכיל את הקבוצה אותה הוא פורש
כלומר אם ת"מ 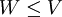 מקיים
מקיים 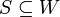 אזי
אזי 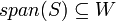
הוכחה
אם 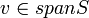 אזי קיימים וקטורים וסקלרים
אזי קיימים וקטורים וסקלרים 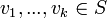 ,
, 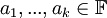 כך שמתקיים
כך שמתקיים 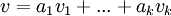 .
מתוך הנתון ש
.
מתוך הנתון ש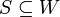 נובע ש
נובע ש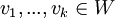 ולכן מתוך סגירות לכפל וסקלר וחיבור
ולכן מתוך סגירות לכפל וסקלר וחיבור 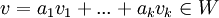 משל.
משל.
הערה: אם 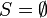 קבוצה ריקה אזי מגדירים פורמאלית כי
קבוצה ריקה אזי מגדירים פורמאלית כי 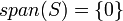
תכונות
יהיה  מ"ו. יהיו
מ"ו. יהיו 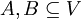 תתי קבוצות ו
תתי קבוצות ו 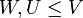 תתי מרחבים. אזי
תתי מרחבים. אזי
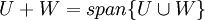 , וכפי שאמרנו הסכום הינו תת המרחב הקטן ביותר המכיל את שני תתי המרחבים.
, וכפי שאמרנו הסכום הינו תת המרחב הקטן ביותר המכיל את שני תתי המרחבים. - בתירגול הקודם ראינו כי
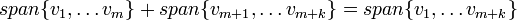
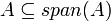
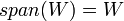 (רק אם
(רק אם 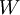 ת"מ!)
ת"מ!)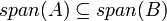
- מסקנה
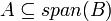 אזי
אזי 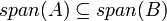 (הוכחה
(הוכחה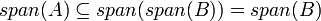 )
)
תרגילים
תרגיל 1
במרחב הוקטורי 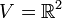 מעל
מעל 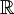 נגדיר
נגדיר
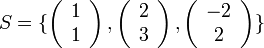
מצא עבור אילו 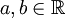 מתקיים כי
מתקיים כי
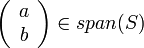
פתרון
שאלה שקולה: עבור אילו 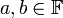 קיימים סקלארים
קיימים סקלארים 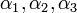 כך ש
כך ש
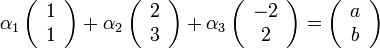
שזה בעצם לשאול האם למערכת
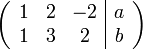 יש פתרון.
יש פתרון.
נדרג ונבדוק
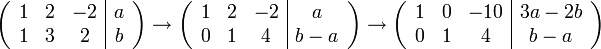
כלומר יש פתרון למערכת (אפילו אינסוף פתרונות) ולכן לכל
 מתקיים כי
מתקיים כי
כלומר 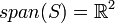
תרגיל 2
במרחב הוקטורי 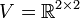 מעל
מעל 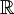 נגדיר
נגדיר
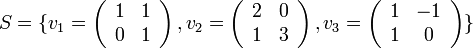
מהו 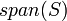 ?
?
פתרון
שאלה שקולה: עבור אילו 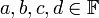 קיימים סקלארים
קיימים סקלארים 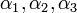 כך ש
כך ש
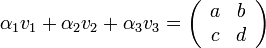
אם נייצג כל מטריצה באמצעות וקטור. למשל
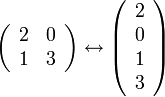
נוכל להחליף את המשוואה לעיל במשואאה
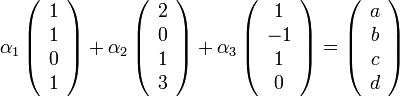
(שימו לב שאלו בדיוק אותם ארבעת המשוואות).
כעת נוכל פשוט לשאול האם למערכת
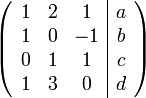 יש פתרון
יש פתרון
נדרג ונבדוק:
עיבוד הנוסחה נכשל (שגיאת תחביר): \left(\begin{array}{ccc|c} 1 & 2 & 1 & a\\ 1 & 0 & -1 & b\\ 0 & 1 & 1 & c\\ 1 & 3 & 0 & d \end{array}\right)\to\left(\begin{array}{ccc|c} 1 & 0 & -1 & b\\ 0 & 1 & 1 & c\\ 1 & 3 & 0 & d\\ 1 & 2 & 1 & a \end{array}\right)\to\\\left(\begin{array}{ccc|c} 1 & 0 & -1 & b\\ 0 & 1 & 1 & c\\ 0 & 3 & 1 & d-b\\ 0 & 2 & 2 & a-b \end{array}\right)\to\left(\begin{array}{ccc|c} 1 & 0 & -1 & b\\ 0 & 1 & 1 & c\\ 0 & 0 & -2 & d-b-3c\\ 0 & 0 & 0 & a-b-2c \end{array}\right)
רואים שיש פתרון אמ"מ 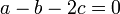
לכן התשובה הסופית היא
עיבוד הנוסחה נכשל (שגיאת תחביר): span(S)=\{\left(\begin{array}{cc} a & b\\ c & d \end{array}\right)\,|\,a-b-2c=0\}= \{\left(\begin{array}{cc} b+2c & b\\ c & d \end{array}\right)\,|\,b,c,d\in \mathbb{R}\} = \\ \{ b\left(\begin{array}{cc} 1 & 1\\ 0 & 0 \end{array}\right)+c\left(\begin{array}{cc} 2 & 0\\ 1 & 0 \end{array}\right)+d\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \,|\,b,c,d\in \mathbb{R}\} = span\{\left(\begin{array}{cc} 1 & 1\\ 0 & 0 \end{array}\right),\left(\begin{array}{cc} 2 & 0\\ 1 & 0 \end{array}\right),\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right)\}
תלות לינארית
דיברנו על כך שצירופים לינאריים הינם כל הסכומים (כולל כפל בסקלרים) של הוקטורים הנתונים. אם נסתכל על פרישה באופן גיאומטרי, אנו רואים שעל ידי וקטורים נפרשים: קו ישר, מישור, מרחב או משהו 4 מימדי ומעלה. כעת, אנו רוצים לראות אילו מהוקטורים "מיותר" כלומר, אם אנחנו יודעים ש10 וקטורים פורשים מישור מסויים, כמה וקטורים מהם אפשר להסיר ועדיין לקבל את אותו המישור? במקרה וניתן להסיר וקטור כלשהו, קבוצה הוקטורים תקרא תלויה לינארית.
באופן פורמאלי:
הגדרות:
יהא  מ"ו מעל
מ"ו מעל  . יהיו וקטורים
. יהיו וקטורים 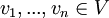 כלשהם אזי
כלשהם אזי
- הצ"ל הטריוואלי הוא צירוף לינארי שכל המקדמים שווים 0 (ואז גם הצירוף שלהם שווה 0). כלומר הצירוף לינארי
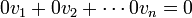 .
. - נאמר ש
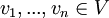 בילתי תלויים לינארית אם אם הצ"ל היחידי שמתאפס הוא הצ"ל הטרוויאלי. באופן שקול אם יש צ"ל שמתאפס אזי הוא הצ"ל הטרוויאלי. ובסימונים:
בילתי תלויים לינארית אם אם הצ"ל היחידי שמתאפס הוא הצ"ל הטרוויאלי. באופן שקול אם יש צ"ל שמתאפס אזי הוא הצ"ל הטרוויאלי. ובסימונים: 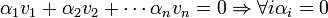
-
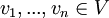 יקראו תלויים לינארית אם הם לא בלתי תלויים לינארית. באופן שקול אם קיימים סקלרים
יקראו תלויים לינארית אם הם לא בלתי תלויים לינארית. באופן שקול אם קיימים סקלרים 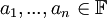 לא כולם אפס כך שמתקיים
לא כולם אפס כך שמתקיים 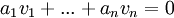
הגדרה (הכלל): קבוצה 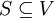 נקראת תלוייה לינארית אם קיימת בתוכה קבוצה סופית כלשהי של וקטורים, כך שוקטוריה תלויים לינארית לפי ההגדרה לעיל. [לא נתעסק בקורס זה בקבוצת אינסופיות בת"ל, אבל אתם יותר ממוזמנים לנסות לחשוב על מרחב וקטורי בעל קבוצה אינסופית בת"ל של וקטורים.]
נקראת תלוייה לינארית אם קיימת בתוכה קבוצה סופית כלשהי של וקטורים, כך שוקטוריה תלויים לינארית לפי ההגדרה לעיל. [לא נתעסק בקורס זה בקבוצת אינסופיות בת"ל, אבל אתם יותר ממוזמנים לנסות לחשוב על מרחב וקטורי בעל קבוצה אינסופית בת"ל של וקטורים.]
הערה: הקבוצה הריקה 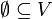 מוגדרת כקבוצה בת"ל.
מוגדרת כקבוצה בת"ל.
דוגמאות
דוגמא 1
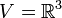 מעל
מעל 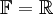
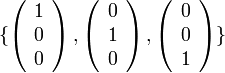 בת"ל כי
בת"ל כי
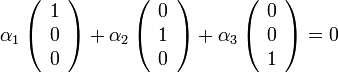
פירושו
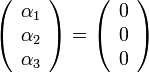
שזה גורר 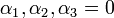 .
.
דוגמא 2
2. (דוגמא מייצגת) 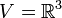 מעל
מעל 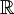 . האם הקבוצה
. האם הקבוצה
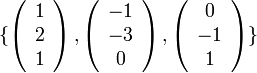 בת"ל?
בת"ל?
נתבונן ב
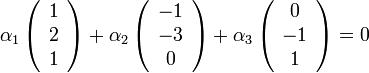 ונמיר אותו להצגה מטריצית
ונמיר אותו להצגה מטריצית
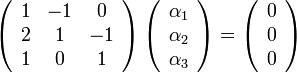
כעת השאלה שקולה האם יש פתרון לא טריאלי למערכת. נדרג ונבדוק
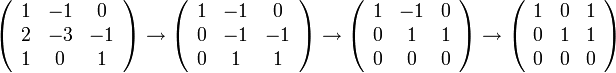
לכל הצבה 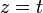 נקבל
נקבל
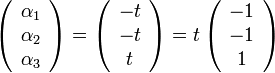 פתרון לא טרוויאלי. כלומר הוקטורים הנ"ל ת"ל.
פתרון לא טרוויאלי. כלומר הוקטורים הנ"ל ת"ל.
אם רוצים לראות את זה מפורש ניקח למשל 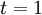 ונקבל צ"ל לא טריוואלי שמתאפס
ונקבל צ"ל לא טריוואלי שמתאפס
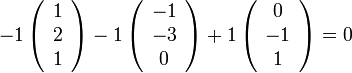
דוגמא 3
יהי 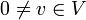 אזי
אזי 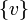 קבוצה בת"ל.
קבוצה בת"ל.
לחילופין יהי 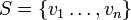 כך ש
כך ש 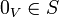 אזי
אזי  ת"ל (ניקח צ"ל שכל המקדמים שווים אפס פרט למקדם של וקטור האפס שניקח להיות שווה 1).
ת"ל (ניקח צ"ל שכל המקדמים שווים אפס פרט למקדם של וקטור האפס שניקח להיות שווה 1).
דוגמא 4
![V=\mathbb{R}_{2}[x]](/images/math/f/7/3/f73cc35842c78e71bd2b26bb136b5c6a.png) מרחב הפלינומים עד דרגה 2 מעל
מרחב הפלינומים עד דרגה 2 מעל 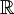 תהא
תהא 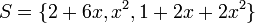 . האם
. האם  בת"ל?
בת"ל?
פתרון: צריך לבדוק האם 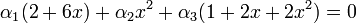 גורר שזה הצ"ל הטריאלי.
גורר שזה הצ"ל הטריאלי.
לפי השוואת מקדמים נקבל כי : 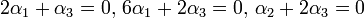
ובצורה מטריצית
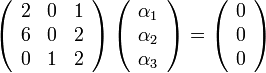
נבדוק אם למערכת יש פתרון לא טריאלי.
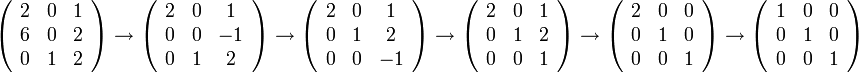
כלומר התשובה היא שלמערכת אין פתרון לא טריאלי. כלומר  בת"ל
בת"ל
דוגמא 5
תרגיל.
האם הפולינומים 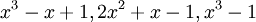 תלויים לינארית?
תלויים לינארית?
פתרון:
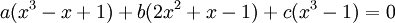 אם"ם
אם"ם
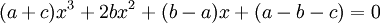 אם"ם
אם"ם
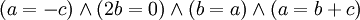 אם"ם
אם"ם
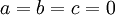
אם כן, הצירוף הלינארי היחיד שמתאפס הינו הטריוויאלי ולכן הפולינומים בת"ל.
משפט
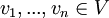 ת"ל אם"ם אחד מהוקטורים הינו צירוף לינארי של האחרים
ת"ל אם"ם אחד מהוקטורים הינו צירוף לינארי של האחרים
הוכחה
הוקטורים ת"ל אם"ם קיימים סקלרים כך ש 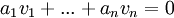 , ולפחות אחד מבין הסקלרים שונה מאפס. נניח ב.ה.כ. (בלי הגבלת הכלליות) ש
, ולפחות אחד מבין הסקלרים שונה מאפס. נניח ב.ה.כ. (בלי הגבלת הכלליות) ש 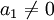 . לכן
. לכן 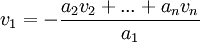 ולכן
ולכן 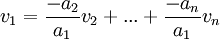 .
.
בכיוון הפוך נניח כי (ב.ה.ב) הוקטור הראשון 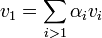 הוא צ"ל של האחרים. אזי
הוא צ"ל של האחרים. אזי 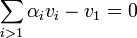 . כלומר קיבלנו צ"ל שמתאפס שיש מקדם אחד לפחות ששונה מאפס (המקדם של
. כלומר קיבלנו צ"ל שמתאפס שיש מקדם אחד לפחות ששונה מאפס (המקדם של 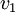 הוא
הוא 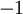 ) על פי הגדרה הוקטורים ת"ל
) על פי הגדרה הוקטורים ת"ל
שימו לב שיצא לנו שהוקטור הראשון תמיד צ"ל של האחרים, כמובן שזה לא נכון. זה נובע רק מטיעון ב.ה.כ שלנו, קל למצוא דוגמאות בהן הוקטור הראשון אינו צ"ל של האחרים.
ממשפט זה קל לנו לראות שהצלחנו בהגדרה שלנו לתלות:
מסקנה: אם 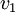 הינו צירוף לינארי של האחרים ניתן להסיר אותו במובן הבא:
הינו צירוף לינארי של האחרים ניתן להסיר אותו במובן הבא: 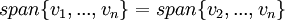 .
.
ושוב, בחזרה למערכות משוואות לינאריות
תרגיל - הקשר בין צירוף לינארי לבין פתרון מערכת משוואות לינאריות=
יהיו 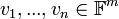 נגדיר
נגדיר 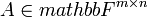 להיות המטריצה שעמודותיה הן
להיות המטריצה שעמודותיה הן 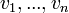 (כלומר
(כלומר 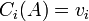 ).
).
יהיה 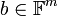 וקטור (פתרון).
וקטור (פתרון).
הוכח כי:
1. 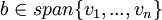 אם"ם קיים פתרון למערכת
אם"ם קיים פתרון למערכת 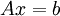
2. במקרה זה הפתרון 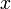 הינו וקטור הסקלרים של הצירוף הלינארי שנותן את b.
כלומר, כאשר
הינו וקטור הסקלרים של הצירוף הלינארי שנותן את b.
כלומר, כאשר 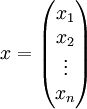 מתקיים
מתקיים 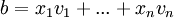
3.נניח והוקטורים שייכים למרחב 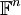 (כלומר
(כלומר 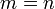 והמטריצה ריבועית). הוכח שקיים צירוף לינארי יחיד הנותן את
והמטריצה ריבועית). הוכח שקיים צירוף לינארי יחיד הנותן את 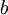 אם"ם המטריצה הינה הפיכה. מה ניתן להסיק על הוקטורים במקרה זה?
אם"ם המטריצה הינה הפיכה. מה ניתן להסיק על הוקטורים במקרה זה?
פתרון
1+2. ישירות מכפל עמודה-עמודה נקבל כי 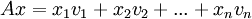 . לפיכך, ברור שקיים פתרון למערכת Ax=b אם"ם קיימים סקלרים כך ש
. לפיכך, ברור שקיים פתרון למערכת Ax=b אם"ם קיימים סקלרים כך ש 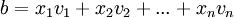 .
.
אמנם התרגיל הזה טריוויאלי למדי אך חשוב מאד לזכור תוצאה זו, היא תשמש אותנו בהמשך רבות. בניסוח קליט: 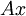 הינה צירוף לינארי של עמודות
הינה צירוף לינארי של עמודות  עם הסקלרים מ-
עם הסקלרים מ-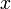 .
.
3. אם המטריצה הפיכה אזי 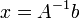 הוא הפתרון היחיד. ולהפיך אם קיים צירוף לינארי יחיד הנותן את
הוא הפתרון היחיד. ולהפיך אם קיים צירוף לינארי יחיד הנותן את 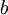 אזי אם נדרג את
אזי אם נדרג את  קנונית נגיע למטריצת היחידה. זה אומר ש
קנונית נגיע למטריצת היחידה. זה אומר ש  הפיכה.
הפיכה.
במקרה זה שהמטריצה הפיכה נסיק כי גם למערכת 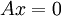 יש פתרון יחיד שהוא
יש פתרון יחיד שהוא 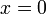 . כלומר צ"ל היחיד של עמודות
. כלומר צ"ל היחיד של עמודות  שמתאפס הוא הצ"ל הטריוויאלי. כלומר עמודות
שמתאפס הוא הצ"ל הטריוויאלי. כלומר עמודות  בת"ל.
בת"ל.
בנוסף, מכיוון שאנו יודעים שמטריצה הפיכה אם"ם המשולחפת שלה הפיכה, ניתן גם להסיק שמטריצה הינה הפיכה אם"ם שורותיה בת"ל.
הצגות שונות של תתי מרחבים
בסעיף זה נראה מספר הצגות לאותו תת מרחב נראה שישנן שלוש דרכים שונות להציג את אותו תת המרחב הוקטורי.
תרגיל.
יהי 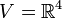 , הוכח ששלוש הקבוצות הבאות שוות:
, הוכח ששלוש הקבוצות הבאות שוות:
פתרון:
נראה שהקבוצה הראשונה שווה לשנייה. וקטור נמצא בspan של קבוצת הוקטורים אם"ם הוא צירוף לינארי שלה. לכן, 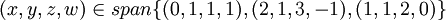 אם"ם קיימים סקלרים a,b,c כך ש
אם"ם קיימים סקלרים a,b,c כך ש 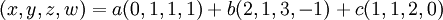 . לכן, הוקטור הוא צ"ל אם"ם קיים פתרון למערכת המשוואות הלינארית על a,b,c כאלה. בעצם, אנו רוצים לאמר על מערכת משוואות פרמטרית מתי יש לה פתרון. נביט במערכת המשוואות:
. לכן, הוקטור הוא צ"ל אם"ם קיים פתרון למערכת המשוואות הלינארית על a,b,c כאלה. בעצם, אנו רוצים לאמר על מערכת משוואות פרמטרית מתי יש לה פתרון. נביט במערכת המשוואות:
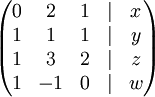
נדרג את המערכת לקבל
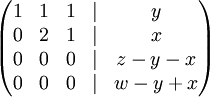
זכרו שלא מעניין אותנו פתרון המערכת, שכן אלו הסקלרים של הצירוף הלינארי. מה שמעניין אותנו הוא האם קיים פתרון למערכת ובמקרה זה קיים פתרון אם"ם 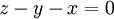 וגם
וגם 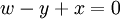 וזו בדיוק הקבוצה השנייה.
וזו בדיוק הקבוצה השנייה.
(שימו לב גם למשפט מתרגול שעבר - b נמצא במרחב העמודות של A אם ורק אם למערכת Ax=b יש פתרון. זה בדיוק מה שקיבלנו בתרגיל זה.)
כעת נראה את השיוויון בין הקבוצה השנייה לשלישית. המרחב הוא בעצם אוסף הפתרונות של מערכת המשוואות הלינארית הנתונה. נדרג אותה והפעם נחפש את הפתרון הכללי.
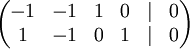
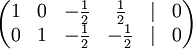
יש שני משתנים תלויים- x,y ושני משתנים חופשיים- z,w. נסמן z=t, w=s ונקבל פתרון כללי מהצורה