הבדלים בין גרסאות בדף "שיחת משתמש:Nimrod"
מתוך Math-Wiki
(←לינארית 2: תרגיל 5, שאלה 3.18) |
(←לינארית 2: תרגיל 5, שאלה 3.18) |
||
| שורה 59: | שורה 59: | ||
</div> | </div> | ||
<span style="float:left;">[[משתמש:אור שחף|אור שחף]][[שיחת משתמש:אור שחף|<sup>שיחה</sup>]]</span> 17:41, 15 בנובמבר 2010 (IST) | <span style="float:left;">[[משתמש:אור שחף|אור שחף]][[שיחת משתמש:אור שחף|<sup>שיחה</sup>]]</span> 17:41, 15 בנובמבר 2010 (IST) | ||
| + | :<math>\lambda</math> ע"ע ולכן מקיים <math>p_A(\lambda)=\sum_{k=0}^na_k\lambda^k=0</math>. לפיכך <math>-\sum_{k=0}^{n-1}a_k\lambda^k=\lambda^n</math> (החסרנו את שני האגפים ב-<math>\sum_{k=0}^{n-1}a_k\lambda^k</math>) ועבור <math>v_0=1</math> זה אכן מתקיים, {{משל}}. | ||
גרסה מ־18:42, 15 בנובמבר 2010
תוכן עניינים
בדידה: תרגיל 1, 4.ג'
צ"ל 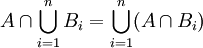 ואח"כ אתה משתמש בזה פעמיים (כדי להראות ש:
ואח"כ אתה משתמש בזה פעמיים (כדי להראות ש: 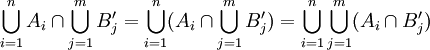 ). -אור שחף, שיחה, 19:01, 26 ביולי 2010 (IDT)
). -אור שחף, שיחה, 19:01, 26 ביולי 2010 (IDT)
לינארית: תרגיל 1, 2.8א
אתה רוצה להראות ש-![\frac{1}{a+b\sqrt{p}} \in \mathbb{F}[\sqrt{p}]](/images/math/d/d/7/dd7df529bb078476cb4e7a64580f1e5c.png) . מתקיים:
. מתקיים: 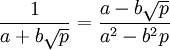 . מכיוון ש-
. מכיוון ש-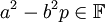 הטענה נכונה. -אור שחף, שיחה, 18:46, 27 ביולי 2010 (IDT)
הטענה נכונה. -אור שחף, שיחה, 18:46, 27 ביולי 2010 (IDT)
![\left(a^2-b^2 p\right)^{-1} \in \mathbb{F} \subset \mathbb{F}[\sqrt{p}]](/images/math/4/0/7/4070ea82ced46be53a16b8802b7c9f08.png) ולכן
ולכן 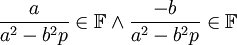 . לפי הגדרת
. לפי הגדרת ![\mathbb{F}[\sqrt{p}]](/images/math/3/5/7/35773cd80c4131ea2053d357c0cc77aa.png) ולפי דיסטריביוטיביות (שאותה צ"ל, זה קל) נובע ש-
ולפי דיסטריביוטיביות (שאותה צ"ל, זה קל) נובע ש-![\frac{a-b\sqrt{p}}{a^2-b^2 p} \in \mathbb{F}[\sqrt{p}]](/images/math/8/0/e/80edb33d38eb027c0169cc471c6432bc.png) ואז, לפי
ואז, לפי  (צ"ל),
(צ"ל), 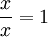 ואסוציאטיביות (צ"ל) מתקיים
ואסוציאטיביות (צ"ל) מתקיים ![\frac{a-b\sqrt{p}}{a^2-b^2 p} = \frac{1}{a+b\sqrt{p}} \in \mathbb{F}[\sqrt{p}]](/images/math/b/d/e/bde6b032f576a7162acca0800a2a1212.png) . -אור שחף, שיחה, 19:44, 27 ביולי 2010 (IDT)
. -אור שחף, שיחה, 19:44, 27 ביולי 2010 (IDT)
לינארית: תרגיל 2, 5.16; 6.19; 6.20;
אני לא בטוח מה זאת אומרת "הרעיונות הכללים", אבל תבדוק אם כבר ענו על מה שאתה צריך כאן, כאן, כאן, כאן, כאן, כאן, כאן, כאן וכאן. אם יש משהו שאתה עדיין לא מבין, תשאל. -אור שחף, שיחה, 16:56, 7 באוגוסט 2010 (IDT)
- בקשר ל-5.16, מגדירים את
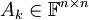 כך ש:
כך ש:  (כאשר
(כאשר 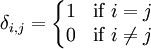 היא הדלתא של קרונקר), ומחשבים לפי
היא הדלתא של קרונקר), ומחשבים לפי 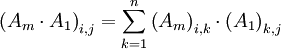 . -אור שחף, שיחה, 19:43, 7 באוגוסט 2010 (IDT)
. -אור שחף, שיחה, 19:43, 7 באוגוסט 2010 (IDT)
לצערי לא הצלחתי להבין את 6.20 אשמח אם תוכל להסביר לי (ואשמח אם תוכל להסביר לי שנית מחר את 5.16 בשביל שאהיה בטוח שהבנתי נכון את הפתרון)
הצמוד של שורש של פולינום
כל המקדמים ממשיים, לכן:

לינארית: תרגיל 3, דף נלווה, שאלה 2d
אכן  (ויקיפדיה הגרמנית, כאשר
(ויקיפדיה הגרמנית, כאשר  )
)
לינארית: תרגיל 5, שאלה 2.11
נגדיר 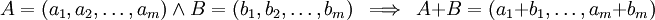 .
.
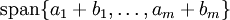
|

|
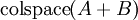
|
||||
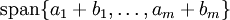 הם צ"ל של הם צ"ל של 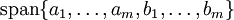 , לכן: , לכן:
|
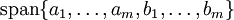
|
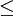
|
||||
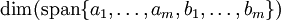
|
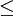
|
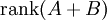
|
| |||
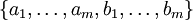 תלויים לינארית ב- תלויים לינארית ב- ו- ו-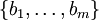
|
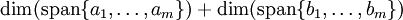
|
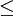
|
||||
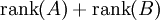
|

|

char
מאפיין של שדה בויקיפדיה. זה הופך את שאלה 11 בחלק ב' למאוד קלה.
- זה עדיין לא ברור
- עבור
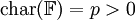 מתקיים
מתקיים 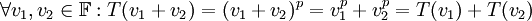 וכן
וכן 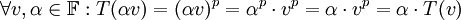 ולכן ה"ל.
ולכן ה"ל.
- עבור
לינארית 2: תרגיל 5, שאלה 3.18
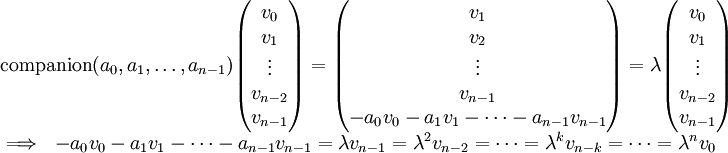
אור שחףשיחה 17:41, 15 בנובמבר 2010 (IST)
 ע"ע ולכן מקיים
ע"ע ולכן מקיים 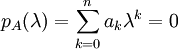 . לפיכך
. לפיכך  (החסרנו את שני האגפים ב-
(החסרנו את שני האגפים ב-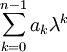 ) ועבור
) ועבור  זה אכן מתקיים,
זה אכן מתקיים,  .
.
![a^2-b^2 p \in \mathbb{F}[\sqrt{p}]](/images/math/e/6/9/e694d6913259da057f288509b94b92b3.png) . ניסיתי להוכיח סגירות:
. ניסיתי להוכיח סגירות:  . בזכות הגדרת
. בזכות הגדרת 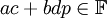 , אבל בגלל קיום איבר נגדי, איבר הופכי וסגירות החיבור והכפל ב-F, צריך להתקיים ש-p שייך ל-F. חכו רגע, או שטעיתי או שיש פה משהו מתוחכם שלא ראיתי. נ.ב. נמרוד, למה מחקת? -
, אבל בגלל קיום איבר נגדי, איבר הופכי וסגירות החיבור והכפל ב-F, צריך להתקיים ש-p שייך ל-F. חכו רגע, או שטעיתי או שיש פה משהו מתוחכם שלא ראיתי. נ.ב. נמרוד, למה מחקת? -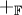 זהה ל-
זהה ל-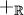 , ולכן קל להוכיח באינדוקציה ש-
, ולכן קל להוכיח באינדוקציה ש-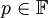 . -
. -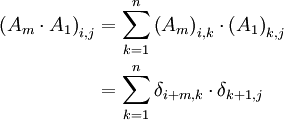 . אנו מחפשים מתי
. אנו מחפשים מתי 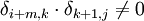 :
: 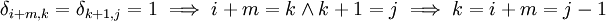 יאדה, יאדה, יאדה, לכן
יאדה, יאדה, יאדה, לכן 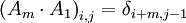 . נותר להוכיח ש-
. נותר להוכיח ש-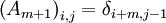 (זה קל), מש"ל. -
(זה קל), מש"ל. -