גרסה מ־16:01, 18 בנובמבר 2010

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

ארכיון

שאלות

שאלה 1 תרגיל 6

האם שאלה 1 תרגיל 6 הכוונה למתבדר/מתכנס במובן הרחב או במובן הצר?

תשובה

במובן הצר. כלומר מתכנס = מתכנס לגבול ממשי ומתבדר = לא מתכנס לגבול ממשי. --ארז שיינר 16:52, 16 בנובמבר 2010 (IST)

טור מתבדר

אם טור מתבדר אז אפשר להגיד ש0.5 טור גם מתבדר??

תשובה

יש משפט שאומר שאם 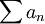$\sum a_n$ מתכנס אז גם $\sum 2\cdot a_n$ מתכנס. תסיק לבד --ארז שיינר 22:57, 16 בנובמבר 2010 (IST)

שאלה כללית

בכדי להראות שאפסילון גדול 1\שורש n אפשר להישתמש בארכימדס ואם כן אז איך בדיוק?

תשובה

לא רוצים להראות שאפסילון גדול מאחד חלק שורש n אלא רוצים להראות שקיים n שמקיים את אי השיוויון הנ"ל. לכן, רוצים n שמקיים את אי השיוויון 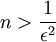$n>\frac{1}{\epsilon^2}$ (העלאנו בריבוע ועשינו 'אחד חלקי').

עכשיו 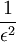$\frac{1}{\epsilon^2}$ מספר ממשי ולכן לפי ארכימדס קיים מספר טבעי גדול ממנו, כפי שרצינו.

עוד שאלה כללית:]

צריך לדעת \ לכתוב בתרגיל [כלשהו] את ההוכחה לכך שהגבול של שורש n של n הוא 1? , או שמספיק לומר "ידוע שהגבול של an="..." הוא 1?

תשובה

אם זה לא התרגיל עצמו לא חייבים לדעת לפתור, אבל ייתכן שיבקשו מכם לפתור את זה. --ארז שיינר 22:31, 17 בנובמבר 2010 (IST)

הבהרת מושגים

לפני כשבוע כתבתי sup{an}, וארז, אמרת שזה סימון לא נכון ושזה לא קיים, אך כך הגדרנו בהרצאה ובתרגול את הסופ' של הקבוצה של איברי an מהאיבר הn.

תשובה

אם יש לכם הגדרה כזו, אז מצויין, תשתמשו בה, כל עוד אתם מבינים שמדובר בעצם על 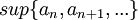$sup\{a_n,a_{n+1},...\}$ . כל מרצה/מתרגל יכול להשתמש בסימונים שלו, אבל המהות נשארת אחת. --ארז שיינר 22:30, 17 בנובמבר 2010 (IST)

תרגיל 6

האם בטורים קיים משפט הסנדוויץ?

תשובה

לא יודע אם למדנו בכיתה, אבל זה נובע ישירות ממשפט הסנדוויץ של סדרות. אם 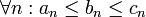$\forall n: a_n\leq b_n \leq c_n$ אזי גם 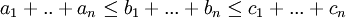$a_1+..+a_n \leq b_1+...+b_n \leq c_1 + ...+ c_n$ ולכן אם 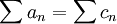$\sum a_n = \sum c_n$ אז סדרות הסכומים החלקיים של הטורים האלה שואפות לאותו מספר. לפי משפט הסנדביץ לסדרות, סדרת הסכומים החלקיים של 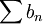$\sum b_n$ מתכנסת לאותו מספר גם כן ולפיכך הטור. --ארז שיינר 00:12, 18 בנובמבר 2010 (IST)

גדולללללל

בואנה אדווה כל הכבודדדד! חבר'ה תסתכלו על פתרון של תרגיל 5 יש הוסיפו שמה דרך פתרון נוספת שאדווה חשבה עליה....

שאלה 1 תרגיל 6

האם מותר להשתמש במשפט הבא:"אם טור מתכנס איברו הכללי שואף ל-0 (מופיע בספר של ד. מייזלר)?

תשובה

כן, גם קל להוכיח את זה. --ארז שיינר 14:20, 18 בנובמבר 2010 (IST)

שאלה

האם אחד מהמשפטים הבאים קיים וניתן להשתמש בו ללא הוכחה?

-אם 1 חלקי an שואפת לאפס אז |an| שואף לאינסוף?

-אם 1 חלקי an שואפת לאפס וan סדרה עולה וחיובית אז an שואף לאינסוף?

תודה!

עוד שאלה

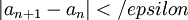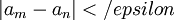אם אני רוצה להוכיח שסדרה מתכנסת על פי הקריטריון של קושי. האם זה טריוויאלי מספיק להגיד שאפשר להוכיח את הטענה ע"י להראות ש $|a_{n+1}-a_n|</epsilon$ במקום $|a_m-a_n|</epsilon$ ? אם לא, האם אפשר להוכיח את הטענה בקצרה במקום בצורה מלאה עם אינדוקציה?

@@ שורה 76: / שורה 76: @@
 :-אם 1 חלקי an שואפת לאפס וan סדרה עולה וחיובית אז an שואף לאינסוף?
 תודה!
+== עוד שאלה ==
+אם אני רוצה להוכיח שסדרה מתכנסת על פי הקריטריון של קושי. האם זה טריוויאלי מספיק להגיד שאפשר להוכיח את הטענה ע"י להראות ש <math>|a_{n+1}-a_n|</epsilon</math> במקום  <math>|a_m-a_n|</epsilon</math> ?
+אם לא, האם אפשר להוכיח את הטענה בקצרה במקום בצורה מלאה עם אינדוקציה?

הבדלים בין גרסאות בדף "שיחה:88-132 סמסטר א' תשעא"

גרסה מ־16:01, 18 בנובמבר 2010

תוכן עניינים

הוספת שאלה חדשה

ארכיון

שאלות

שאלה 1 תרגיל 6

תשובה

טור מתבדר

תשובה

שאלה כללית

תשובה

עוד שאלה כללית:]

תשובה

הבהרת מושגים

תשובה

תרגיל 6

תשובה

גדולללללל

שאלה 1 תרגיל 6

תשובה

שאלה

עוד שאלה

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים