הבדלים בין גרסאות בדף "שיחה:88-113 סמסטר א' תשעא/קבוצת דיון-עדי ניב"
דורון פרלמן (שיחה | תרומות) |
(←האם צריך להוכיח: פסקה חדשה) |
||
| שורה 24: | שורה 24: | ||
במידה ונצליח לפתור את תרגיל האתגר, מה בדיוק צריך לעשות עם הפתרון? האם לשלוח אותו למרצה? ואם כן אז איך בדיוק? [[משתמש:לידור.א.|-לידור.א.-]] 21:43, 4 בדצמבר 2010 (IST) | במידה ונצליח לפתור את תרגיל האתגר, מה בדיוק צריך לעשות עם הפתרון? האם לשלוח אותו למרצה? ואם כן אז איך בדיוק? [[משתמש:לידור.א.|-לידור.א.-]] 21:43, 4 בדצמבר 2010 (IST) | ||
:אתה יכול לשלוח אימייל לד"ר צבאן, הכתובת רשומה באתר שלו http://u.cs.biu.ac.il/~tsaban/ . [[משתמש:דורון פרלמן|דורון פרלמן]] 22:20, 4 בדצמבר 2010 (IST) | :אתה יכול לשלוח אימייל לד"ר צבאן, הכתובת רשומה באתר שלו http://u.cs.biu.ac.il/~tsaban/ . [[משתמש:דורון פרלמן|דורון פרלמן]] 22:20, 4 בדצמבר 2010 (IST) | ||
| + | |||
| + | == האם צריך להוכיח == | ||
| + | |||
| + | לגבי שתי הטענות הבאות: | ||
| + | -לכל מרחב ממימד סופי יש בסיס; | ||
| + | -כל בסיס אפשר להפוך לבסיס א"נ ע"י תהליך גראם שמידט- | ||
| + | האם ניתן להגיד "כפי שעשינו בהרצאה" או "על פי משפט" וכו', או שצריך להוכיח אותן (מחדש)? תודה! | ||
גרסה מ־21:38, 4 בדצמבר 2010
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
ארכיון
שאלות
כמה שאלות עם החומר שנלמד לאחרונה
שלום,
החומר שנלמד לאחרונה, על מכפלה פנימית, בסיסים אורתונורמליים וכדומה לא יושב אצלי טוב. גיליתי שמאוד עוזר אם מבינים מה המקבילים של המושגים שלמדנו במרחב (כמו ניצבות, מכפלה פנימית=מכפלה סקלרית וכו'). אך לכמה לא מצאתי מקבילים ולכן קשה לי להבין בדיוק מה הם אומרים או למה הם משמשים. דבר ראשון, האם יש מקביל לבסיס אורתוגונלי או אורתונורמלי במרחב, ואם כן למה צריך אותו? ודבר שני, למה, או האם יש מקביל במרחב, לכך שההיטל של וקטור (על תת מרחב, ביחס לבסיס אורתונורמלי B={w1,..,wk} ) הוא 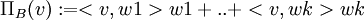 ?
תודה!
?
תודה!
אני לא בטוחה למה אתה מתכוון מקביל במרחב אבל בסיס אורתוגונלי במרחב יושב על הצירים או על כל הזזה שלהם בו ללא הזזה שלהם אחד ביחס לשני. "צריך" אורתוג' כי יותר נוח לעבוד איתו מבחינה של זוית ואורתונ' כי יותר נוח לעבוד איתו מבחינה של אורך (בשניהם "יותר נוח" הכוונה במכפלה הפנימית). לגבי החלק השני : כי אתה יוצר צרוף לנארי שלו מההטלה שלו לכל תת מרחב שכל וקטור בסיס יוצר. ראה אילוסטרציה מאת דר' צבאן בעמוד הראשי.
תרגיל האתגר
במידה ונצליח לפתור את תרגיל האתגר, מה בדיוק צריך לעשות עם הפתרון? האם לשלוח אותו למרצה? ואם כן אז איך בדיוק? -לידור.א.- 21:43, 4 בדצמבר 2010 (IST)
- אתה יכול לשלוח אימייל לד"ר צבאן, הכתובת רשומה באתר שלו http://u.cs.biu.ac.il/~tsaban/ . דורון פרלמן 22:20, 4 בדצמבר 2010 (IST)
האם צריך להוכיח
לגבי שתי הטענות הבאות: -לכל מרחב ממימד סופי יש בסיס; -כל בסיס אפשר להפוך לבסיס א"נ ע"י תהליך גראם שמידט- האם ניתן להגיד "כפי שעשינו בהרצאה" או "על פי משפט" וכו', או שצריך להוכיח אותן (מחדש)? תודה!