הבדלים בין גרסאות בדף "שיחה:88-132 סמסטר א' תשעא"
(←שאלה (קשור לרציפות)) |
(←תשובה) |
||
| שורה 206: | שורה 206: | ||
וכן, אם יש רציפות במ"ש על A אז יש רציפות במ"ש בכל קטע המוכל בA. --[[משתמש:ארז שיינר|ארז שיינר]] 20:19, 5 בינואר 2011 (IST) | וכן, אם יש רציפות במ"ש על A אז יש רציפות במ"ש בכל קטע המוכל בA. --[[משתמש:ארז שיינר|ארז שיינר]] 20:19, 5 בינואר 2011 (IST) | ||
| + | |||
| + | :תודה. אבל לא למדנו שום דבר שימושי לזה... רק שאם פונקציה רציפה בקטע סגור אז היא רציפה במידה שווה, ואת ההגדרה. | ||
== שאלה (קשור לרציפות) == | == שאלה (קשור לרציפות) == | ||
גרסה מ־21:35, 5 בינואר 2011
תוכן עניינים
- 1 הוספת שאלה חדשה
- 2 ארכיון
- 3 שאלות
- 3.1 תרגיל 11 שאלה 2
- 3.2 שאלה אל רציפות במ"ש
- 3.3 שאלה
- 3.4 תרגיל 10 שאלה 4
- 3.5 תרגיל 11-שאלה 4, סעיף A
- 3.6 תרגיל 10- שאלה 6 - סעיף c
- 3.7 תרגיל 11 שאלה 1
- 3.8 תרגיל 10 שאלה 2
- 3.9 תרגיל 10 שאלה 7
- 3.10 תרגיל 10- שאלה 2
- 3.11 רציפות פונקציה
- 3.12 תרגיל 11 שאלה 4
- 3.13 משפט ערך הביניים
- 3.14 תרגיל 10 שאלה 7 b
- 3.15 צריך להסביר?
- 3.16 log(x)=log10(x) או ln(x)?
- 3.17 פונקציה לא רציפה במ"ש
- 3.18 תרגיל 12
- 3.19 בחינות משנים קודמות
- 3.20 שלילת רציפות במ"ש
- 3.21 תרגיל 12 שאלה 4
- 3.22 לגבי הפתרון של תרגיל 10, שאלה 7, ג'
- 3.23 הוכחת רציפות במידה שווה
- 3.24 שאלה (קשור לרציפות)
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
ארכיון
- ארכיון 1
- ארכיון 2
- ארכיון 3
- ארכיון 4
- ארכיון 5
- ארכיון 6
- ארכיון 7
- ארכיון 8
- ארכיון 9
- ארכיון 10
- ארכיון 11
- ארכיון 12
שאלות
תרגיל 11 שאלה 2
בתרגיל 2 הכוונה לרציפות במ"ש בקטע סופי?
- אממ... שיהיה בקטע כלשהו, זה לא ממש משנה. --ארז שיינר 14:21, 29 בדצמבר 2010 (IST)
שאלה אל רציפות במ"ש
פונקציה מחזורית רציפה במידה שווה בגלל שהיא חסומה? האם כל הפונקציות מחזוריות רציפות במ"ש?
- לא. חסימות לא גורר רציפות במ"ש. יש משפט שפונקציה מחזורית שרציפה בכל הממשיים היא רציפה במ"ש. --ארז שיינר 16:22, 29 בדצמבר 2010 (IST)
שאלה
האם ההרכבה של פונקציה מחזורית אל פונקציה שאינה מחזורית היא גם מחזורית?
- לא בהכרח. למשל
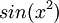 אינה מחזורית. אבל הרכבה של פונקציה כלשהי על פונקציה מחזורית היא תמיד מחזורית, למשל
אינה מחזורית. אבל הרכבה של פונקציה כלשהי על פונקציה מחזורית היא תמיד מחזורית, למשל 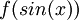 מחזורית לכל f. --ארז שיינר 23:35, 29 בדצמבר 2010 (IST)
מחזורית לכל f. --ארז שיינר 23:35, 29 בדצמבר 2010 (IST)
תרגיל 10 שאלה 4
בקשר לזה שצריך שהפונקציה תהיה חסומה מלעיל ומלרע בקטע [0,1) - אז העובדה שהפו' צריכה להיות רציפה גם ב1 עצמו לא סותר את זה שהיא תהיה חסומה? כי כל הפונקציות שאני מוצא שמתאימות לתרגיל, יש להן אסימפטוטות ב0 (שבו שהפו' שואפת למינוס אינסוף) וב1 (שבו הפו' שואפת לאינסוף), אבל העובדה שצריך שהפו' תהיה רציפה גם ב 1 עצמו הורסת את הדוגמאות הנגדיות מכיוון שהפונקציות ששואפות לאינסוף ב1, לא מוגדרות ב1. אפשר עזרה/הכוונה לגבי העניין הזה? תודה!
- אתה מתכוון וודאי ללא חסומה במקום חסומה. זה נכון, בצד של אחד הפונקציה חייבת להיות חסומה. לכן אי אפשר לקחת פונקציה ששואפת לאינסוף או למינוס אינסוף באפס כי אז אתה מאבד אחד מהם. צריך למצוא פונקציה שגם עולה וגם יורדת באפס. --ארז שיינר 23:36, 29 בדצמבר 2010 (IST)
- פונקציה רציפה שמתכנסת גם לאינסוף וגם למינוס אינסוף?? (זה לא נשמע כזה הגיוני)
- נראה לי שמצאתי פונקציה טובה. תודה
- פונקציה רציפה שמתכנסת גם לאינסוף וגם למינוס אינסוף?? (זה לא נשמע כזה הגיוני)
תרגיל 11-שאלה 4, סעיף A
האם הרכבה של פונק' לא רציפה על פונק' רציפה,בהכרח לא רציפה?
תשובה
ממש לא, גם לגבי במ"ש וגם רציפות רגילה.
רציפות רגילה: ניקח  אזי
אזי 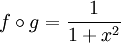
רציפות במ"ש: ניקח 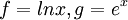 . בקטע
. בקטע 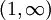 הפונקציה lnx רציפה במ"ש בעוד e^x אינה רציפה במ"ש אבל ההרכבה שלהן x רציפה במ"ש.
הפונקציה lnx רציפה במ"ש בעוד e^x אינה רציפה במ"ש אבל ההרכבה שלהן x רציפה במ"ש.
--ארז שיינר 23:33, 29 בדצמבר 2010 (IST)
תרגיל 10- שאלה 6 - סעיף c
בטוח שצריך להיות קטן שווה ולא קטן ממש? (בכל מקרה, תמיד מותר לי להגיד שאם a קטן ממש מ-b הוא גם קטן שווה ל-b, נכון?)
- כן, זה לא משנה, מה שקטן ממש הוא בפרט קטן שווה. --ארז שיינר 23:37, 29 בדצמבר 2010 (IST)
תרגיל 11 שאלה 1
אפשר כיוון/ דרך לפתרון? חשבתי על זה הרבה ואין לי שמץ של מושג מאיפה להתחיל אפילו..
- מה יכולים להיות ההפרשים בציר y אם הפונקציה שואפת לגבול מסוים? --ארז שיינר 19:40, 30 בדצמבר 2010 (IST)
תרגיל 10 שאלה 2
שאם אפשר להשתמש בכך שאפשר לחלק כל פונקציה רציפה לקטעים בהם היא מונוטונית?\
- הצלחתי גם בלי זה, אבל בכל מקרה, זה בסדר?
- דבר ראשון אני לא בטוח מאיפה המשפט הזה ובאיזה תנאים הוא נכון אם בכלל. שנית, אני לא רואה את הקשר לתרגיל, זה תרגיל למשפט ערך הביניים. --ארז שיינר 19:14, 1 בינואר 2011 (IST)
תרגיל 10 שאלה 7
האם צריך להוכיח דברים שקשה מאוד להוכיח אותם כגון בסעיף ב' שהפונקציה שואפת לאינסוף מהכיוון החיובי כאשר X שואף ל 2^(nPie) מהכיוון החיובי? או שאפשר להגיד את זה?
- זה לא קשה מאד להוכיח. אפשר להשתמש במשפט שאם פונקציה חיובית ושואפת לאפס אז אחד חלקי הפונקציה שואף לאינסוף. --ארז שיינר 21:53, 3 בינואר 2011 (IST)
תרגיל 10- שאלה 2
אפשר בבקשה כיוון/רמז?
- מצטרף לבקשה
- (רמז לא ממתרגל) אתה נדרש להוכיח שקיים
 עבורו
עבורו 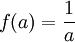 . מהי הפונקציה הכי פשוטה עליה אתה מסוגל לחשוב בה
. מהי הפונקציה הכי פשוטה עליה אתה מסוגל לחשוב בה 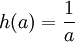 ? בנה בעזרת שתי אלו פונקציה אחרת כך שהפונקציה תתאפס בנקודה שתעזור לך להוכיח את הדרוש (הראה כי הפונקציה אכן מתאפסת!). גל א.
? בנה בעזרת שתי אלו פונקציה אחרת כך שהפונקציה תתאפס בנקודה שתעזור לך להוכיח את הדרוש (הראה כי הפונקציה אכן מתאפסת!). גל א. - רמז אחר (גם לא מתרגל): משפט ערך הביניים אומר שלכל ערך קבוע (שאינו תלוי במקור) בין
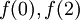 יש מקור בין 0 ל-2. שנה את הפונקציה כך שתצטרך למצוא מקור לערך קבוע במקום ל-
יש מקור בין 0 ל-2. שנה את הפונקציה כך שתצטרך למצוא מקור לערך קבוע במקום ל- . נ"ב: מתי עזרה עוברת את הגבול המותר והופכת למתן תשובה? כלומר, עד כמה מותר לנו לעזור אחד לשני?
. נ"ב: מתי עזרה עוברת את הגבול המותר והופכת למתן תשובה? כלומר, עד כמה מותר לנו לעזור אחד לשני?
- ברגע שהקורא לא תופס רעיון אלא מעתיק את השורות אחת לאחת. --ארז שיינר 21:43, 1 בינואר 2011 (IST)
- (רמז לא ממתרגל) אתה נדרש להוכיח שקיים
רציפות פונקציה
האם פונקציה רציפה היא פונקציה מונוטונית (לא עולה/לא יורדת) ולהפך - מונוטונית היא רציפה? תודה!
- פונקציה מונוטנית היא רציפה אם אין לה שום נקודת אי רציפות, ופונקציה רציפה לא בהכרח מונוטינית (דוגמא: x^2)... אני משארת שהתכוונת לשאול על רציפות במ"ש אבל גם אז.. פונקציה מונוטונית אומנם רציפה במידה שווה אבל פונקציה אשר רציפה במידה שווה לא מונוטונית בהכרח...
- לעניות דעתי פונקציה מונוטונית אינה בהכרח רציפה במ"ש כפי שכתבת, אפילו אם היא רציפה. לדוגמה הפונקציה שנתת x^2 בקטע R+. -לידור.א.- 22:30, 31 בדצמבר 2010 (IST)
- מונוטונית ממש לא חייבת להיות רציפה במ"ש, הרי רציפות במ"ש מתרחשת כאשר יש חסם על מהירות הפונקציה. אם היא שואפת ממש מהר לאינסוף היא לא תהיה רציפה במ"ש. להפך, אם פונקציה רציפה במ"ש היא יכול להיות מחזורית כמו סינוס (למשל) ולכן לא חייבת להיות מונוטונית. --ארז שיינר 19:16, 1 בינואר 2011 (IST)
- לעניות דעתי פונקציה מונוטונית אינה בהכרח רציפה במ"ש כפי שכתבת, אפילו אם היא רציפה. לדוגמה הפונקציה שנתת x^2 בקטע R+. -לידור.א.- 22:30, 31 בדצמבר 2010 (IST)
תרגיל 11 שאלה 4
האם כשאני שולל רציפות במ"ש של פונקציה לפי נגיד זה שהיא לא רציפה בחלק מהתחום, אני צריך לתת דוגמא של של סדרות כדי להפריך רציפות במ"ש.
- לא, יש משפט לפיו רציפה במ"ש היא רציפה בכל נקודה. אם היא לא רציפה בנקודה מסוימת אז היא לא רציפה במ"ש בגלל המשפט. אם היא לא מוגדרת באיזו נקודה, אז ממש ברור שהיא לא רציפה במ"ש (כי ההגדרה של רציפה במ"ש דורשת מוגדרות). --ארז שיינר 19:37, 1 בינואר 2011 (IST)
משפט ערך הביניים
הוכחנו אותו עבור פונקציה רציפה בקטע סגור. האם הוא נכון גם עבור פונקציה רציפה בקטע פתוח?
בהוכחה, נראה שלנתון הזה שהקטע סגור יש משמעות, כי השתמשו בלמה של קאנטור (עבור קטעים מקוננים), ובה חשוב שהקטעים הם סגורים - ושוב, אני לא רואה את החשיבות, גם בלמה.
תשובה
בוא תנסה לנסח את המשפט בקטע פתוח, ואז לחשוב לבד אם הוא נכון, זה תרגיל קל (גם עשינו אותו בכיתה פחות או יותר). --ארז שיינר 19:39, 1 בינואר 2011 (IST)
- הבנתי את הבעיתיות. אם a ו-b הם הקצוות של הקטע הפתוח, אז קודם כל, לא בהכרח קיים
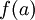 . אם הוא קיים, יכול להיות שהוא מאוד רחוק משאר התמונות של הפונקציה, כי לא נתון שהיא רציפה שם.
. אם הוא קיים, יכול להיות שהוא מאוד רחוק משאר התמונות של הפונקציה, כי לא נתון שהיא רציפה שם.
- יפה. יותר מזה, לא נתון האם בכלל קיים גבול חד צדדי שם. קח למשל את
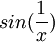 . איך תנסח את המשפט לגביו בקטע (0,1)? אפשר לנסח משפט על הקטע הפתוח כאשר הגבולות החד צדדיים קיימים. מוכיחים את המשפט באמצעות לקחת קטע סגור המוכל בקטע הפתוח, שקצותיו רחוקים מרחק אפסילון מקצות הקטע המקורי. --ארז שיינר 21:39, 1 בינואר 2011 (IST)
. איך תנסח את המשפט לגביו בקטע (0,1)? אפשר לנסח משפט על הקטע הפתוח כאשר הגבולות החד צדדיים קיימים. מוכיחים את המשפט באמצעות לקחת קטע סגור המוכל בקטע הפתוח, שקצותיו רחוקים מרחק אפסילון מקצות הקטע המקורי. --ארז שיינר 21:39, 1 בינואר 2011 (IST)
- משהו כמו: "תהי f פונקציה רציפה בקטע
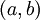 . אזי לכל
. אזי לכל 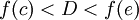 (קטן-שווה) קיים d בקטע
(קטן-שווה) קיים d בקטע 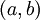 כך ש-
כך ש- 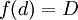 , כאשר לכל
, כאשר לכל 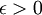 מתקיים
מתקיים 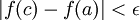 וגם
וגם 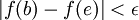 "? יש למשפט הזה שם? אפשר להשתמש בו?
"? יש למשפט הזה שם? אפשר להשתמש בו?
- לא לא. לא הזכרת כלל את הגבולות החד צדדים, ואני בתיאור שלי דברתי על ההוכחה ולא על המשפט. המשפט לדוגמא יהיה: תהי f מוגדרת בקטע (a,b) כך ש
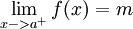 וגם
וגם 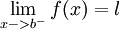 , אני לכל
, אני לכל 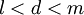 קיימת נקודה c בקטע הפתוח (a,b) כך ש
קיימת נקודה c בקטע הפתוח (a,b) כך ש 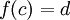 . ההוכחה היא באמצעות הקטנת הקטע באפסילון מסויים מכל צד. --ארז שיינר 02:20, 2 בינואר 2011 (IST)
. ההוכחה היא באמצעות הקטנת הקטע באפסילון מסויים מכל צד. --ארז שיינר 02:20, 2 בינואר 2011 (IST) - אגב, אם לכל אפסילון מתקיים
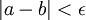 אז בהכרח מתקיים a=b. --ארז שיינר 02:20, 2 בינואר 2011 (IST)
אז בהכרח מתקיים a=b. --ארז שיינר 02:20, 2 בינואר 2011 (IST)
- אמממ.. אוקיי (לגבי המשפט). למה מתקיים a=b? ואם ככה, אז איך מבטאים את "המספר הקרוב ביותר שיש" ל-a? נניח שיש לי קטע (a,b) ואני רוצה לבטא את האיבר ה"ראשון" שבתוך הקטע הזה - למרות שברור שהוא לא קיים באמת.
- נו, אני לא מבין את השאלה. אם ברור שהוא לא קיים, איך אפשר לבטא אותו? אין סימון לדברים שאינם קיימים, ואין מספר קרוב ביותר. מתקיים a=b מהסיבה שהמספר היחיד שקטן מכל גודל חיובי הינו אפס. היה לכם תרגיל כזה בהתחלת השנה --ארז שיינר 01:56, 5 בינואר 2011 (IST)
- אמממ.. אוקיי (לגבי המשפט). למה מתקיים a=b? ואם ככה, אז איך מבטאים את "המספר הקרוב ביותר שיש" ל-a? נניח שיש לי קטע (a,b) ואני רוצה לבטא את האיבר ה"ראשון" שבתוך הקטע הזה - למרות שברור שהוא לא קיים באמת.
- לא לא. לא הזכרת כלל את הגבולות החד צדדים, ואני בתיאור שלי דברתי על ההוכחה ולא על המשפט. המשפט לדוגמא יהיה: תהי f מוגדרת בקטע (a,b) כך ש
- משהו כמו: "תהי f פונקציה רציפה בקטע
- יפה. יותר מזה, לא נתון האם בכלל קיים גבול חד צדדי שם. קח למשל את
תרגיל 10 שאלה 7 b
מותר לעשות קירוב על פי טורי טיילור עבור x->0?
- לא, לא למדנו טורי טיילור בקורס. --ארז שיינר 19:39, 1 בינואר 2011 (IST)
צריך להסביר?
בתרגיל 10, שאלה 4 מצאתי פונקציה  כך שקיימת תת סדרה
כך שקיימת תת סדרה 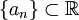 שעבורה
שעבורה  וסדרה
וסדרה 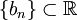 שעבורה
שעבורה  . זה מספיק מפורט כדי להסביר ש-
. זה מספיק מפורט כדי להסביר ש- אינה חסומה מלעיל ואינה חסומה מלרע? תודה.
אינה חסומה מלעיל ואינה חסומה מלרע? תודה.
- (לא מתרגלת) אבל היא אמורה להיות לא חסומה מלעיל ולא חסומה מלרע בקטע [0,1)...
- את צודקת, אז מה אם אני מפרט גם ש-
![\{a_n\},\{b_n\}\subset(0,1]](/images/math/8/b/4/8b403dfd828f6f8fb2129c0e5e213b4a.png) ?
?
- את צודקת, אז מה אם אני מפרט גם ש-
- כן, זה בהחלט מספיק ישירות מההגדרה של חסימות (הסדרות מוכיחות שאין חסם). --ארז שיינר 19:41, 1 בינואר 2011 (IST)
log(x)=log10(x) או ln(x)?
רק ליתר ביטחון, כשכתוב בש"ב log הכוונה היא ל-ln או ל-log10? או שזה בכלל log2?
- לא מתרגלת: log בלי בסיס זה אומר בסיס 10.
- אצל זלצמן Log הוא תמיד lan. אבל זה באמת לא משנה לאף תרגיל באופן מהותי, כי הרי ההבדל בין בסיסים שונים של הלוג הוא סה"כ כפל בקבוע. --ארז שיינר 19:40, 1 בינואר 2011 (IST)
פונקציה לא רציפה במ"ש
יש דרך לדעת בקלות שפונקציה היא לא רציפה במ"ש? לדוגמה, הייתי בטוח ש fx=x^2 היא רבמ"ש, אבל מישהו כאן אמר שהיא לא. איך יודעים? תודה
- ראה בוויקיפדיה. אולי יעניין אותך לדעת שפרופ' עוזי ו. תרם לערך כ-1,400 בתים מתוך ה-12,800 שהוא כולל.
תרגיל 12
האם יש אפשרות שיפורסם בהקדם האפשרי? בשבוע שעבר פורסם תרגיל 11 רק ביום שלישי, דבר שיצא מאוד לא נוח מכיוון שכל הזמן של יום שני בו אפשר לפתור את התרגיל בעצם הופך לזמן "מת".
- מצטרפת
- יפורסם היום בערב --ארז שיינר 12:21, 3 בינואר 2011 (IST)
בחינות משנים קודמות
שלום רב, לקראת הבחינה הקרבה ברצוני (וברצונם של אחרים שדיברתי איתם) לעשות שאלות חזרה מבחינות קודמות... האם יש סיכוי להעלות לכאן בחינות קודמות (עדיף עם פתרונות, אבל אפשר גם בלי) כדי שנוכל לתרגל? תודה, גל א.
- אתה מוזמן להסתכל באתר www.studenteen.org, בו יש בחינות משנים קודמות גם באינפי 1.
- מכיר את האתר וראיתי את הבחינות שבו. ובכל זאת, ברצוני לשאול האם קיימות בחינות קצת יותר מעודכנות, ובמידת האפשר האם אפשר להעלות בחינות עם פתרונות? תודה מראש.
- אני (ארז) לא אספק עוד בחינות ופתרונות פרט לבחינה של זלצמן שמימלא נמצאת כבר ברובה בשיעורי הבית. מומלץ לבקש בחינות מהעבר ישירות מהמרצים. --ארז שיינר 23:42, 3 בינואר 2011 (IST)
- מכיר את האתר וראיתי את הבחינות שבו. ובכל זאת, ברצוני לשאול האם קיימות בחינות קצת יותר מעודכנות, ובמידת האפשר האם אפשר להעלות בחינות עם פתרונות? תודה מראש.
שלילת רציפות במ"ש
אני רוצה לבדוק את עצמי: האם שלילת רציפות במ"ש (בקטע) אומרת שקיים אפסילון גדול מאפס שבשבילו לכל דלתא גדול מאפס ול-x1,x2 מסוימים (קיימים) כך ש אם |x1-x2|<דלתא אז |fx1-fx2|<אפסילון ? תודה!
- (לא מתרגלת) אני חושבת שזה צריך להיות גדול או שווה אפסילון.
- צודקת, גדול שווה אפסילון --ארז שיינר 23:47, 4 בינואר 2011 (IST)
תרגיל 12 שאלה 4
האם אפשר להתייחס לlog בתור ln?
- אצל זלצמן log אם"ם ln --ארז שיינר 23:41, 3 בינואר 2011 (IST)
- (מישהו אחר) - אז רק כדי לוודא, בשאלה 4, האם ה-log שם הוא ln? אני לא סטודנט של זלצמן (תיכוניסט), מה שרלוונטי לי כרגע האם בשאלה זה ln או log10, כי אני עדיין לא סגור על זה.
- רק ln --ארז שיינר 13:23, 5 בינואר 2011 (IST)
- (מישהו אחר) - אז רק כדי לוודא, בשאלה 4, האם ה-log שם הוא ln? אני לא סטודנט של זלצמן (תיכוניסט), מה שרלוונטי לי כרגע האם בשאלה זה ln או log10, כי אני עדיין לא סגור על זה.
לגבי הפתרון של תרגיל 10, שאלה 7, ג'
השאלה שהייתה בשיעורים (לא במבחן):
נכון, לפי היינה הגבול לא קיים, אבל זה יכול להיות גם סוג ראשון - גבולות חד צדדיים קיימים ושונים. צריך לבדוק את האפשרות הזו, לא? אני מפספספת משהו?
- לא קיים גבול חד צדדי, הרציונאלים זה לא "צד". גבול חד צדדי ימני זה אם לכל הסדרות
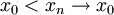 מתקיים
מתקיים 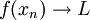 אז הגבול החד צדדי הימני הוא L. זה ממש לא המצב פה. --ארז שיינר 00:42, 5 בינואר 2011 (IST)
אז הגבול החד צדדי הימני הוא L. זה ממש לא המצב פה. --ארז שיינר 00:42, 5 בינואר 2011 (IST)
- אז בעצם במהלך הבדיקה, הוכחת שיש גבול חד צדדי שלא קיים?
- שני הגבולות החד צדדיים לא קיימים. רק צריך להחליף שם בפתרון את
 ב
ב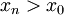 (או קטן) --ארז שיינר 15:57, 5 בינואר 2011 (IST)
(או קטן) --ארז שיינר 15:57, 5 בינואר 2011 (IST)
- שני הגבולות החד צדדיים לא קיימים. רק צריך להחליף שם בפתרון את
- אז בעצם במהלך הבדיקה, הוכחת שיש גבול חד צדדי שלא קיים?
הוכחת רציפות במידה שווה
בתרגיל 11, באילו משפטים שמשמשים להוכחת או שלילת רציפות במידה שווה מותר להשתמש? אפשר לקבל רשימה של המשפטים האלו? (וראיתי כבר את הערך בויקיפדיה - האם מותר להשתמש בכל המשפטים שכתובים שם?)
עוד דבר, רק לוודא - אם צריך להוכיח רציפות במידה שווה בקטע פתוח, אז אפשר להוכיח רציפות בקטע אחר, סגור - שמכיל אותו, ואז היא רציפה במידה שווה בקטע הגדול, ולכן גם בקטן, נכון?
תשובה
תלוי מה למדתם בהרצאה ובתרגיל שלכם.
וכן, אם יש רציפות במ"ש על A אז יש רציפות במ"ש בכל קטע המוכל בA. --ארז שיינר 20:19, 5 בינואר 2011 (IST)
- תודה. אבל לא למדנו שום דבר שימושי לזה... רק שאם פונקציה רציפה בקטע סגור אז היא רציפה במידה שווה, ואת ההגדרה.
שאלה (קשור לרציפות)
זה נכון שלכל פונקציה רציפה בקטע, לדוגמה (אינסוף,a) כך שהפונקציה לא שואפת לאינסוף בגבולות (גם כשאיקס שואף לאינסוף אז הפונקציה רק שואפת למספר סופי וכו') אז לכל סדרה x_n מתקיים ש f(x_n) חסומה ( ולכן קיימת ת"ס x_n_k כך ש f(x_n_k) מתכנסת)? ואם זה נכון, צריך להוכיח את זה? תודה
- מה זה כו'? במתמטיקה מדייקים, לא אומרים וכו'. אם הפונקציה חסומה (וזה לא נובע בהכרח מזה שהיא לא מתכנסת לאינסוף) אז מה שרשמת נכון. כמו כן, אין לזה קשר לרציפות. --ארז שיינר 20:21, 5 בינואר 2011 (IST)
- אם מתקיימים התנאים בשאלה 1 תרגיל 11, זה נכון?????
- איך זה יעזור שם למצוא תת סדרה מתכנסת? --ארז שיינר 21:14, 5 בינואר 2011 (IST)
- הוכחנו בהרצאה בעזרת ת"ס מתכנס שפונקציה היא רציפה במ"ש כאשר נתון שהיא רציפה בקטע הסגור [a,b]. חשבתי להשתמש בהוכחה דומה מאוד לזאת שעשינו בכיתה רק בהתאמה לתנאי השאלה הנתונה, ולכן אם אני לא טועה, אז תנאי השאלה צריכים להביא לת"ס מתכנסת ובכך לפתרון נכון של השאלה.
- המממ... אני לא בטוח לגבי הכיוון הזה, לצערי אני לא מכיר את ההוכחה שציינת. אני מנחש שהרעיון שם הוא שx_n_k עצמה מתכנסת, ומכיוון שפה התחום הינו אינסופי זה לא יעזור. תנסה להבין מה העובדה שהפונקציה מתכנסת באינסוף אומר על ההפרשים בציר הy. --ארז שיינר 22:39, 5 בינואר 2011 (IST)
- הוכחנו בהרצאה בעזרת ת"ס מתכנס שפונקציה היא רציפה במ"ש כאשר נתון שהיא רציפה בקטע הסגור [a,b]. חשבתי להשתמש בהוכחה דומה מאוד לזאת שעשינו בכיתה רק בהתאמה לתנאי השאלה הנתונה, ולכן אם אני לא טועה, אז תנאי השאלה צריכים להביא לת"ס מתכנסת ובכך לפתרון נכון של השאלה.
- איך זה יעזור שם למצוא תת סדרה מתכנסת? --ארז שיינר 21:14, 5 בינואר 2011 (IST)
- אם מתקיימים התנאים בשאלה 1 תרגיל 11, זה נכון?????