גרסה מ־21:33, 8 בינואר 2011

חזרה לדף הקורס

גלול לתחתית העמוד

תוכן עניינים

1 הוספת שאלה חדשה
2 ארכיון
3 שאלות

הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

ארכיון

שאלות

תרגיל 12 שאלה 4

האם אפשר להתייחס לlog בתור ln?

אצל זלצמן log אם"ם ln --ארז שיינר 23:41, 3 בינואר 2011 (IST)

(מישהו אחר) - אז רק כדי לוודא, בשאלה 4, האם ה-log שם הוא ln? אני לא סטודנט של זלצמן (תיכוניסט), מה שרלוונטי לי כרגע האם בשאלה זה ln או log10, כי אני עדיין לא סגור על זה.

רק ln --ארז שיינר 13:23, 5 בינואר 2011 (IST)

לגבי הפתרון של תרגיל 10, שאלה 7, ג'

השאלה שהייתה בשיעורים (לא במבחן):

נכון, לפי היינה הגבול לא קיים, אבל זה יכול להיות גם סוג ראשון - גבולות חד צדדיים קיימים ושונים. צריך לבדוק את האפשרות הזו, לא? אני מפספספת משהו?

לא קיים גבול חד צדדי, הרציונאלים זה לא "צד". גבול חד צדדי ימני זה אם לכל הסדרות

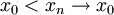x_0<x_n\rightarrow x_0

מתקיים

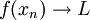f(x_n)\rightarrow L

אז הגבול החד צדדי הימני הוא L. זה ממש לא המצב פה. --ארז שיינר 00:42, 5 בינואר 2011 (IST)

אז בעצם במהלך הבדיקה, הוכחת שיש גבול חד צדדי שלא קיים?

שני הגבולות החד צדדיים לא קיימים. רק צריך להחליף שם בפתרון את

x_n\neq x_0

ב

x_n>x_0

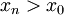(או קטן) --ארז שיינר 15:57, 5 בינואר 2011 (IST)

הוכחת רציפות במידה שווה

בתרגיל 11, באילו משפטים שמשמשים להוכחת או שלילת רציפות במידה שווה מותר להשתמש? אפשר לקבל רשימה של המשפטים האלו? (וראיתי כבר את הערך בויקיפדיה - האם מותר להשתמש בכל המשפטים שכתובים שם?)

עוד דבר, רק לוודא - אם צריך להוכיח רציפות במידה שווה בקטע פתוח, אז אפשר להוכיח רציפות בקטע אחר, סגור - שמכיל אותו, ואז היא רציפה במידה שווה בקטע הגדול, ולכן גם בקטן, נכון?

תשובה

תלוי מה למדתם בהרצאה ובתרגיל שלכם.

וכן, אם יש רציפות במ"ש על A אז יש רציפות במ"ש בכל קטע המוכל בA. --ארז שיינר 20:19, 5 בינואר 2011 (IST)

תודה. אבל לא למדנו שום דבר שימושי לזה... רק שאם פונקציה רציפה בקטע סגור אז היא רציפה במידה שווה, ואת ההגדרה.

להוכחה:

המשפט הראשון בתרגיל, שניתן להכליל אותו כך: תהי פונקציה רציפה בקטע A (גם לא סופי). אם יש לה גבולות סופיים בקצות הקטע (גם אם קצה הקטע הוא אינסוף) אזי היא רציפה במ"ש בקטע.
פונקציה מחזורית שרציפה על כל הממשיים - רציפה במ"ש בכל הממשיים.
הרכבה של רציפות במ"ש הינה רציפה במ"ש. (יש לשים לב שהפונקציה החיצונית רציפה במ"ש על התמונה של הפנימית, למעשה).
סכום של רציפות במ"A הינה רציפה במ"ש (אבל כפל לא - x^2=xx).
תהי f פונקציה רציפה. אם הנגזרת של f חסומה בקטע אזי f רציפה בו במ"ש

לשלילה:

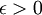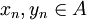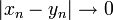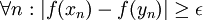אם קיים $\epsilon > 0$ וקיימות שתי סדרות $x_n,y_n \in A$ המקיימות: $|x_n-y_n|\rightarrow 0$ וגם $\forall n: |f(x_n)-f(y_n)|\geq \epsilon$ אזי הפונקציה f אינה רציפה במ"ש בקטע A.
אם פונקציה אינה חסומה בקטע סופי אזי היא אינה רציפה בו במ"ש.
אם פונקציה אינה רציפה או אינה מוגדרת בקטע היא אינה רציפה בו במ"ש.

תודה רבה! חשבתי שאסור להשתמש במשפט עם הנגזרת החסומה, כי עוד לא למדנו אותו. הוא מאוד שימושי! הוא לא אם ורק אם? כלומר, הנגזרת של פונקציה רציפה במידה שווה היא לא בהכרח חסומה?

שוב, אני לא יודע עם מי אתה לומד. אסור עקרונית להשתמש בנגזרת כרגע אצלנו כי לא למדנו את זה, אבל אני אלמד בראשון וזה יהיה בחומר למבחן של זלצמן. בקשר לשאלה השנייה - לא, זה לא אםם, קח כדוגמא נגדית את שורש איקס בקטע (0,1). ההפרש בין ערכי הפונקציה אמנם קטן, אבל השיפוע של הפונקציה באיזור 0 שואף לאינסוף (אפילו שיש לה גבול סופי) --ארז שיינר 03:01, 6 בינואר 2011 (IST)

אה, נכון. טוב אז באילו משפטים מותר למי שלומד אצלך להשתמש?

כל מה שאמרתי פרט לנגזרת. --ארז שיינר 11:13, 6 בינואר 2011 (IST)

טוב, תודה רבה

שאלה (קשור לרציפות)

זה נכון שלכל פונקציה רציפה בקטע, לדוגמה (אינסוף,a) כך שהפונקציה לא שואפת לאינסוף בגבולות (גם כשאיקס שואף לאינסוף אז הפונקציה רק שואפת למספר סופי וכו') אז לכל סדרה x_n מתקיים ש f(x_n) חסומה ( ולכן קיימת ת"ס x_n_k כך ש f(x_n_k) מתכנסת)? ואם זה נכון, צריך להוכיח את זה? תודה

מה זה כו'? במתמטיקה מדייקים, לא אומרים וכו'. אם הפונקציה חסומה (וזה לא נובע בהכרח מזה שהיא לא מתכנסת לאינסוף) אז מה שרשמת נכון. כמו כן, אין לזה קשר לרציפות. --ארז שיינר 20:21, 5 בינואר 2011 (IST)

אם מתקיימים התנאים בשאלה 1 תרגיל 11, זה נכון?????

איך זה יעזור שם למצוא תת סדרה מתכנסת? --ארז שיינר 21:14, 5 בינואר 2011 (IST)

הוכחנו בהרצאה בעזרת ת"ס מתכנס שפונקציה היא רציפה במ"ש כאשר נתון שהיא רציפה בקטע הסגור [a,b]. חשבתי להשתמש בהוכחה דומה מאוד לזאת שעשינו בכיתה רק בהתאמה לתנאי השאלה הנתונה, ולכן אם אני לא טועה, אז תנאי השאלה צריכים להביא לת"ס מתכנסת ובכך לפתרון נכון של השאלה.

המממ... אני לא בטוח לגבי הכיוון הזה, לצערי אני לא מכיר את ההוכחה שציינת. אני מנחש שהרעיון שם הוא שx_n_k עצמה מתכנסת, ומכיוון שפה התחום הינו אינסופי זה לא יעזור. תנסה להבין מה העובדה שהפונקציה מתכנסת באינסוף אומר על ההפרשים בציר הy. --ארז שיינר 22:39, 5 בינואר 2011 (IST)

שהם סופיים? אבל אני לא מצליח להגיע מזה לשום דבר.

מה הכוונה בהפרשים סופיים? כל מספר ממשי הוא סופי. --ארז שיינר 23:33, 8 בינואר 2011 (IST)

תרגיל 12

ארז, איך כותבים את הפונקציה arctanx לפי Cosx ןsinx?? תודה!

אי אפשר. זה ההופכית של tg. כלומר:

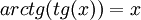arctg(tg(x))=x

--ארז שיינר 01:39, 7 בינואר 2011 (IST)

מחזוריות

יש דרך קלה להוכיח שפונקציה היא מחזורית? תודה

להראות שקיים a כך ש

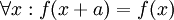\forall x: f(x+a)=f(x)

--ארז שיינר 14:38, 7 בינואר 2011 (IST)

תודה רבה

תרגיל 12 שאלה 2

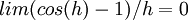
האם מותר להגיד ש $lim(cos(h)-1)/h=0$

כשh שואף ל0

כן.

@@ שורה 85: / שורה 85: @@
 :::::המממ... אני לא בטוח לגבי הכיוון הזה, לצערי אני לא מכיר את ההוכחה שציינת. אני מנחש שהרעיון שם הוא שx_n_k עצמה מתכנסת, ומכיוון שפה התחום הינו אינסופי זה לא יעזור. תנסה להבין מה העובדה שהפונקציה מתכנסת באינסוף אומר על ההפרשים בציר הy. --[[משתמש:ארז שיינר|ארז שיינר]] 22:39, 5 בינואר 2011 (IST)
 ::::::שהם סופיים? אבל אני לא מצליח להגיע מזה לשום דבר.
+:::::::מה הכוונה בהפרשים סופיים? כל מספר ממשי הוא סופי. --[[משתמש:ארז שיינר|ארז שיינר]] 23:33, 8 בינואר 2011 (IST)
 == תרגיל 12 ==

הבדלים בין גרסאות בדף "שיחה:88-132 סמסטר א' תשעא"

גרסה מ־21:33, 8 בינואר 2011

תוכן עניינים

הוספת שאלה חדשה

ארכיון

שאלות

תרגיל 12 שאלה 4

לגבי הפתרון של תרגיל 10, שאלה 7, ג'

הוכחת רציפות במידה שווה

תשובה

שאלה (קשור לרציפות)

תרגיל 12

מחזוריות

תרגיל 12 שאלה 2

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים