הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/3.4.11"
(יצירת דף עם התוכן "=מבוא לאינטגרציה נומרית {{הערה|(המשך)}}= בהרצאה הקודמת הצגנו את כלל סימפסון לקירוב האינטגרל ...") |
|||
| (6 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
=מבוא לאינטגרציה נומרית {{הערה|(המשך)}}= | =מבוא לאינטגרציה נומרית {{הערה|(המשך)}}= | ||
בהרצאה הקודמת הצגנו את כלל סימפסון לקירוב האינטגרל המסויים והראנו שהטעות בחישוב בקטע <math>[a,b]</math> חסומה ע"י <math>\max_{x\in[a,b]}\left|f^{(4)}(x)\right|\frac{h^4(b-a)}{45}</math> כאשר h המרחק בין שתי נקודות סמוכות בחלוקה שבחרנו. ניתן גישה אחרת למציאת הטעות, שהיא יותר קצרה ונותנת ערך יותר קטן לחסם של הטעות, אבל היא פחות אינטואיטיבית: | בהרצאה הקודמת הצגנו את כלל סימפסון לקירוב האינטגרל המסויים והראנו שהטעות בחישוב בקטע <math>[a,b]</math> חסומה ע"י <math>\max_{x\in[a,b]}\left|f^{(4)}(x)\right|\frac{h^4(b-a)}{45}</math> כאשר h המרחק בין שתי נקודות סמוכות בחלוקה שבחרנו. ניתן גישה אחרת למציאת הטעות, שהיא יותר קצרה ונותנת ערך יותר קטן לחסם של הטעות, אבל היא פחות אינטואיטיבית: | ||
| − | + | הראנו שמספיק לחשב בקירוב <math>\int\limits_{-h}^h f\approx\frac h3\Big(f(-h)+4f(0)+f(h)\Big)</math> כאשר f גזירה 4 פעמים בסביבת 0. נגדיר פונקציה חדשה <math>G(h):=\int\limits_{-h}^h f-\frac h3\Big(f(-h)+4f(0)+f(h)\Big)</math>. G מוגדרת ורציפה בסביבה של 0 וגם (לפי הצבה) <math>G(0)=0</math>. עבור F קדומה ל-f מתקיים (לפי המשפט היסודי){{left|<math>\begin{align}\frac\mathrm d{\mathrm dh}G(h)&=\frac\mathrm d{\mathrm dh}\left(F(h)-F(-h)-\frac h3\Big(f(-h)+4f(0)+f(h)\Big)\right)\\&=f(h)+f(-h)-\frac13\Big(f(-h)+4f(0)+f(h)\Big)-\frac h3\Big(-f'(-h)+f'(h)\Big)\end{align}</math>}} | |
| − | + | לכן <math>\lim_{h\to0}G'(h)=f(0)+f(0)-\frac13\Big(f(0)+4f(0)+f(0)\Big)-0=2f(0)-\frac63f(0)=0</math>. ע"פ הלמה השנייה בהרצאה הקודמת <math>G'(0)</math> קיים ושווה ל-0. נגזור שוב את G ונקבל <math>\lim_{h\to0}G''(h)=0=G''(0)</math>. נמשיך לגזור פעמיים נוספות ונקבל <math>G'''(0)=G^{(4)}(0)=0</math> וגם <math>G^{(4)}(h)=-\frac13\Big(-f'''(-h)+f'''(h)\Big)-\frac h3\Big(f^{(4)}(-h)+f^{(4)}(h)\Big)</math>. עתה: | |
| − | לכן <math>\lim_{h\to0}G'(h)=f(0)+f(0)-\frac13(f(0)+4f(0)+f(0)-0=2f(0)-\frac63f(0)=0</math>. ע"פ הלמה השנייה בהרצאה הקודמת <math>G'(0)</math> קיים ושווה ל-0. נגזור שוב את G ונקבל | + | |
{| | {| | ||
{{=|l=\frac{G(h)}{h^5} | {{=|l=\frac{G(h)}{h^5} | ||
| שורה 23: | שורה 22: | ||
}} | }} | ||
|} | |} | ||
| − | כעת נגדיר <math>M:=\max_{x\in[a,b]}\left|f^{(4)}(x)\right|</math>. לפי משפט לגראנז' קיים <math>c\in(-h,h)</math> כך ש-<math>\frac{f^{(3)}(h)-f^{(3)}(-h)}{2h}=f^{(4)}(c)</math> ולכן <math>\left|f^{(3)}(h)-f^{(3)}(-h)\right|\le2hM</math>. מכל זה נובע {{left|<math>\begin{align}\left|G^{(4)}(h_4)\right|&\le\left|-\frac13\ | + | כעת נגדיר <math>M:=\max_{x\in[a,b]}\left|f^{(4)}(x)\right|</math>. לפי משפט לגראנז' קיים <math>c\in(-h,h)</math> כך ש-<math>\frac{f^{(3)}(h)-f^{(3)}(-h)}{2h}=f^{(4)}(c)</math> ולכן <math>\left|f^{(3)}(h)-f^{(3)}(-h)\right|\le2hM</math>. מכל זה נובע {{left|<math>\begin{align}\left|G^{(4)}(h_4)\right|&\le\left|-\frac13\Big(f^{(3)}(-h_4)+f^{(3)}(h_4)\Big)\right|+\left|\frac{h_4}3\Big(f^{(4)}(-h_4)+f^{(4)}(h_4)\Big)\right|\\&\le\frac{2h_4}3M+\frac{h_4}32M\\&=\frac43Mh_4\end{align}</math>}} |
עתה <math>\left|\frac{G(h)}{h^5}\right|=\left|\frac{G^{(4)}(h_4)}{120h_4}\right|\le\frac1{120h_4}\frac43Mh_4=\frac M{90}</math> וקיבלנו ש-<math>|G(h)|\le\frac{Mh^5}{90}</math>, כלומר הטעות בכל קטע מהסוג <math>[x_{k-1},x_{k+1}]</math> חסומה ע"י <math>\frac{Mh^5}{90}</math>. ב-<math>[a,b]</math> יש <math>\frac n2=\frac{(b-a)}{2h}</math> ולפיכך הטעות חסומה ע"י <math>\frac{b-a}{2h}\cdot\frac{Mh^5}{90}=\frac{Mh^4}{180}(b-a)</math>. {{משל}} | עתה <math>\left|\frac{G(h)}{h^5}\right|=\left|\frac{G^{(4)}(h_4)}{120h_4}\right|\le\frac1{120h_4}\frac43Mh_4=\frac M{90}</math> וקיבלנו ש-<math>|G(h)|\le\frac{Mh^5}{90}</math>, כלומר הטעות בכל קטע מהסוג <math>[x_{k-1},x_{k+1}]</math> חסומה ע"י <math>\frac{Mh^5}{90}</math>. ב-<math>[a,b]</math> יש <math>\frac n2=\frac{(b-a)}{2h}</math> ולפיכך הטעות חסומה ע"י <math>\frac{b-a}{2h}\cdot\frac{Mh^5}{90}=\frac{Mh^4}{180}(b-a)</math>. {{משל}} | ||
===דוגמה=== | ===דוגמה=== | ||
| שורה 30: | שורה 29: | ||
* הקירוב לפי סכום רימן הוא <math>\sum_{k=0}^4f(x_k)h=\frac14\left(1+\frac45+\frac23+\frac47+\frac12\right)\approx\underline{0.6}34523809</math>. | * הקירוב לפי סכום רימן הוא <math>\sum_{k=0}^4f(x_k)h=\frac14\left(1+\frac45+\frac23+\frac47+\frac12\right)\approx\underline{0.6}34523809</math>. | ||
* כעת נעשה קירוב בשיטת הטרפזים: {{left|<math>\frac{f(x_0)+f(x_4)}2h+h\sum_{k=1}^3f(x_k)=\frac18\left(1+\frac12\right)+\frac14\left(\frac45+\frac23+\frac47\right)\approx\underline{0.69}7023792</math>}} | * כעת נעשה קירוב בשיטת הטרפזים: {{left|<math>\frac{f(x_0)+f(x_4)}2h+h\sum_{k=1}^3f(x_k)=\frac18\left(1+\frac12\right)+\frac14\left(\frac45+\frac23+\frac47\right)\approx\underline{0.69}7023792</math>}} | ||
| − | * ולפי סימפסון: {{left|<math>\begin{array}{l}\frac h3\left(f(x_0)+4\sum_{k=1}^{2}f(x_{2k-1})+2\sum_{k=1}^{1}f(x_{2k})+f(x_4)\right)\\=\frac1{12}\left(1+4\ | + | * ולפי סימפסון: {{left|<math>\begin{array}{l}\displaystyle\frac h3\left(f(x_0)+4\sum_{k=1}^{2}f(x_{2k-1})+2\sum_{k=1}^{1}f(x_{2k})+f(x_4)\right)\\=\displaystyle\frac1{12}\left(1+4\tfrac45+2\tfrac23+4\tfrac47+\frac12\right)\\\approx\underline{0.693}253968\end{array}</math>}} נחשב את סדר הגודל של הטעות בקירוב סימפסון: {{left|<math>f'(x)=-x^{-2}\implies f''(x)=2x^{-3}\implies f^{(3)}(x)=-6x^{-4}\implies f^{(4)}(x)=24x^{-5}</math>}} ולכן <math>M=\max_{x\in[1,2]}\left|24x^{-5}\right|=24</math> והטעות R בקירוב מקיימת <math>|R|\le\frac{Mh^4}{180}(2-1)=\frac1{1920}<5.21\cdot10^{-4}</math> |
| − | =אינטגרל לא אמיתי | + | =אינטגרל לא אמיתי, סוג I= |
| − | עד עתה הגדרנו אינטגרלים מסויימים רק עבור פונקציות חסומות בקטעים סופיים. אם הפונקציה לא חסומה ו/או הקטע לא חסום עדיין ניתן להגדיר "אינטגרל לא אמיתי". | + | עד עתה הגדרנו אינטגרלים מסויימים רק עבור פונקציות חסומות בקטעים סופיים. אם הפונקציה לא חסומה ו/או הקטע לא חסום עדיין ניתן להגדיר "אינטגרל לא אמיתי" (improper integral). אינטגרלים של קטעים אינסופיים מהסוג <math>\int\limits_{-\infty}^b f,\ \int\limits_a^\infty f,\ \int\limits_{-\infty}^\infty f</math> הם אינטגרלים לא אמיתיים מסוג 1. |
| − | + | ||
| − | אינטגרלים של קטעים אינסופיים מהסוג <math>\int\limits_{-\infty}^b f,\ \int\limits_a^\infty f,\ \int\limits_{-\infty}^\infty f</math>. | + | |
| − | '''הגדרה''': תהי f פונקציה מוגדרת בקטע מהסוג <math>[a,\infty)</math>. נאמר ש-f אינטגרבילית מקומית בקטע זה אם לכל <math>b>a</math> f אינטגרבילית בקטע <math>[a,b]</math>. | + | '''הגדרה''': תהי f פונקציה מוגדרת בקטע מהסוג <math>[a,\infty)</math>. נאמר ש-f אינטגרבילית מקומית (locally integrable) בקטע זה אם לכל <math>b>a</math> f אינטגרבילית בקטע <math>[a,b]</math>. |
למשל, אם f רציפה למקוטעין אז היא אינטגרבילית מקומית. | למשל, אם f רציפה למקוטעין אז היא אינטגרבילית מקומית. | ||
| − | '''הגדרה:''' תהי f מוגדרת ואינטגרבילית מקומית ב-<math>[a,\infty)</math> נגדיר <math>\int\limits_a^\infty f:=\lim_{R\to\infty}\int\limits_a^R f</math>. אם הגבול קיים נאמר שהאינטגרל מתכנס, אחרת הוא מתבדר. | + | '''הגדרה:''' תהי f מוגדרת ואינטגרבילית מקומית ב-<math>[a,\infty)</math>. נגדיר <math>\int\limits_a^\infty f:=\lim_{R\to\infty}\int\limits_a^R f</math>. אם הגבול קיים נאמר שהאינטגרל מתכנס, אחרת הוא מתבדר. |
אינטגביליות מקומית מוגדרת באופן דומה עבור קטע מהצורה <math>(-\infty,b]</math> ואם f אינטגרבילית מקומית שם נגדיר <math>\int\limits_{-\infty}^b f:=\lim_{R\to-\infty}\int\limits_R^b f</math>. | אינטגביליות מקומית מוגדרת באופן דומה עבור קטע מהצורה <math>(-\infty,b]</math> ואם f אינטגרבילית מקומית שם נגדיר <math>\int\limits_{-\infty}^b f:=\lim_{R\to-\infty}\int\limits_R^b f</math>. | ||
| − | עבור f מוגדרת בכל <math>\mathbb R</math> נאמר שהיא אינטגרבילית מקומית אם היא אינטגרבילית | + | עבור f מוגדרת בכל <math>\mathbb R</math> נאמר שהיא אינטגרבילית מקומית אם היא אינטגרבילית בכל קטע סופי, ואם כן נגדיר <math>\int\limits_{-\infty}^\infty f=\int\limits_{-\infty}^a f+\int\limits_a^\infty f</math> עבור <math>a\in\mathbb R</math> כרצוננו עבורו שני האינטגרלים באגף ימין מתכנסים. |
| − | + | ==דוגמאות== | |
| − | # <math>\int\limits_1^\infty{\mathrm dx}{x^2}</math>. נחשב: {{left|<math>\begin{align}\int&=\lim_{R\to\infty}\int\limits_1^R\frac{\mathrm dx}{x^2}\\&=\lim_{R\to\infty}\left[-\frac1x\right]_{x=1}^R\\&=\lim_{R\to\infty}\left(-\frac1R+1\right)\\&=1\end{align}</math>}} ניתן גם לכתוב בקיצור: <math>\int\limits_1^\infty\frac{\mathrm dx}{x^2}=\left[-\frac1x\right]_{x=1}^\infty=0-(-1)=1</math>. | + | # <math>\int\limits_1^\infty\frac{\mathrm dx}{x^2}</math>. נחשב: {{left|<math>\begin{align}\int&=\lim_{R\to\infty}\int\limits_1^R\frac{\mathrm dx}{x^2}\\&=\lim_{R\to\infty}\left[-\frac1x\right]_{x=1}^R\\&=\lim_{R\to\infty}\left(-\frac1R+1\right)\\&=1\end{align}</math>}} ניתן גם לכתוב בקיצור: <math>\int\limits_1^\infty\frac{\mathrm dx}{x^2}=\left[-\frac1x\right]_{x=1}^\infty=0-(-1)=1</math>. |
# <math>\int\limits_1^\infty\frac{\mathrm dx}x=[\ln|x|]_{x=1}^\infty=\ln(\infty)-0=\infty</math>, כלומר האינטגרל מתבדר (אך מתכנס במובן הרחב). | # <math>\int\limits_1^\infty\frac{\mathrm dx}x=[\ln|x|]_{x=1}^\infty=\ln(\infty)-0=\infty</math>, כלומר האינטגרל מתבדר (אך מתכנס במובן הרחב). | ||
| − | # שאלה מארה"ב מלפני הרבה שנים: חצוצרה אינסופית תתקבל מסיבוב הגרף <math>y=\frac1x</math> סביב ציר ה-x ב-<math>[1,\infty)</math>. | + | # שאלה מארה"ב מלפני הרבה שנים: חצוצרה אינסופית תתקבל מסיבוב הגרף <math>y=\frac1x</math> סביב ציר ה-x ב-<math>[1,\infty)</math>. האם יש מספיק צבע בעולם כדי לצבוע אותה מבפנים?<br/>'''פתרון''': לכאורה התשובה היא לא, כי שטח הפנים של החצוצרה הוא <math>\pi\int\limits_1^\infty\frac2x\sqrt{1+\left(-\frac1{x^2}\right)^2}\mathrm dx>\pi\int\limits_1^\infty\frac2x\mathrm dx=\infty</math>, כלומר אין מספיק צבע. אך מכיוון שכמות הצבע נמדדת ביחידות נפח ולא שטח, ומכיוון שהנפח בתוך החצוצרה הוא <math>\pi\int\limits_1^\infty\frac{\mathrm dx}{x^2}=\pi</math>, יספיקו לנו <math>\pi</math> יחידות מעוקבות של צבע ואפילו ישאר לנו עודף. |
---- | ---- | ||
גרסה אחרונה מ־15:25, 27 ביולי 2011
מבוא לאינטגרציה נומרית (המשך)
בהרצאה הקודמת הצגנו את כלל סימפסון לקירוב האינטגרל המסויים והראנו שהטעות בחישוב בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) חסומה ע"י
חסומה ע"י ![\max_{x\in[a,b]}\left|f^{(4)}(x)\right|\frac{h^4(b-a)}{45}](/images/math/c/0/1/c018af318180ba106c2e556e0a8ce3d2.png) כאשר h המרחק בין שתי נקודות סמוכות בחלוקה שבחרנו. ניתן גישה אחרת למציאת הטעות, שהיא יותר קצרה ונותנת ערך יותר קטן לחסם של הטעות, אבל היא פחות אינטואיטיבית:
כאשר h המרחק בין שתי נקודות סמוכות בחלוקה שבחרנו. ניתן גישה אחרת למציאת הטעות, שהיא יותר קצרה ונותנת ערך יותר קטן לחסם של הטעות, אבל היא פחות אינטואיטיבית:
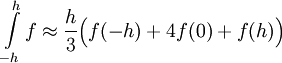 כאשר f גזירה 4 פעמים בסביבת 0. נגדיר פונקציה חדשה
כאשר f גזירה 4 פעמים בסביבת 0. נגדיר פונקציה חדשה 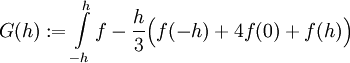 . G מוגדרת ורציפה בסביבה של 0 וגם (לפי הצבה)
. G מוגדרת ורציפה בסביבה של 0 וגם (לפי הצבה)  . עבור F קדומה ל-f מתקיים (לפי המשפט היסודי)
. עבור F קדומה ל-f מתקיים (לפי המשפט היסודי)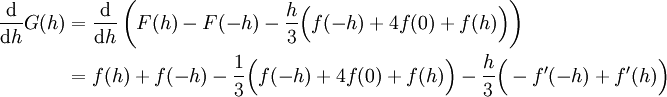
לכן 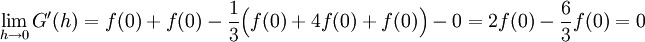 . ע"פ הלמה השנייה בהרצאה הקודמת
. ע"פ הלמה השנייה בהרצאה הקודמת 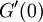 קיים ושווה ל-0. נגזור שוב את G ונקבל
קיים ושווה ל-0. נגזור שוב את G ונקבל 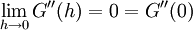 . נמשיך לגזור פעמיים נוספות ונקבל
. נמשיך לגזור פעמיים נוספות ונקבל 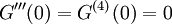 וגם
וגם 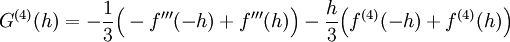 . עתה:
. עתה:
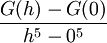
|

|
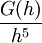
|
||||
לפי משפט קושי קיים 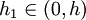 עבורו: עבורו:
|
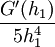
|

|
||||
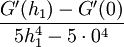
|

|
|||||
קיים 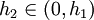 עבורו: עבורו:
|
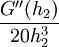
|

|
||||
קיים 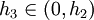 עבורו: עבורו:
|
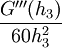
|

|
||||
קיים 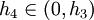 עבורו: עבורו:
|
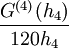
|

|
![M:=\max_{x\in[a,b]}\left|f^{(4)}(x)\right|](/images/math/e/f/c/efc5b75b335a88530d1277770b0ba498.png) . לפי משפט לגראנז' קיים
. לפי משפט לגראנז' קיים 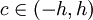 כך ש-
כך ש-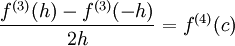 ולכן
ולכן 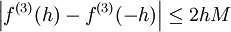 . מכל זה נובע
. מכל זה נובע 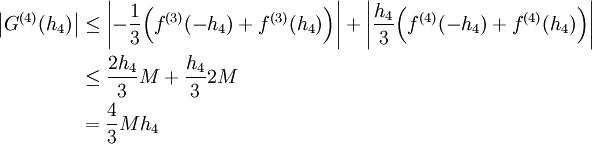
עתה 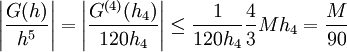 וקיבלנו ש-
וקיבלנו ש-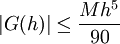 , כלומר הטעות בכל קטע מהסוג
, כלומר הטעות בכל קטע מהסוג ![[x_{k-1},x_{k+1}]](/images/math/8/a/4/8a43f36d9e8f2ce9259f885a5e87cad7.png) חסומה ע"י
חסומה ע"י 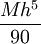 . ב-
. ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) יש
יש 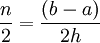 ולפיכך הטעות חסומה ע"י
ולפיכך הטעות חסומה ע"י 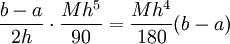 .
. 
דוגמה
נקרב 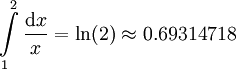 . נבחר
. נבחר 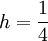 . נציב:
. נציב:
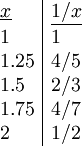
- הקירוב לפי סכום רימן הוא
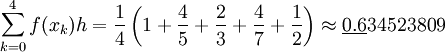 .
. - כעת נעשה קירוב בשיטת הטרפזים:
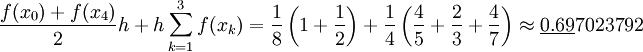
- ולפי סימפסון: נחשב את סדר הגודל של הטעות בקירוב סימפסון:
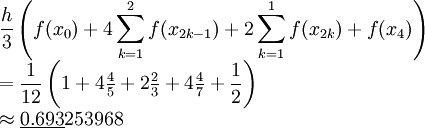 ולכן
ולכן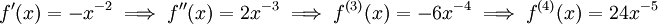
![M=\max_{x\in[1,2]}\left|24x^{-5}\right|=24](/images/math/3/c/b/3cb76e1de290e38b165826c3d0743151.png) והטעות R בקירוב מקיימת
והטעות R בקירוב מקיימת 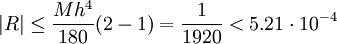
אינטגרל לא אמיתי, סוג I
עד עתה הגדרנו אינטגרלים מסויימים רק עבור פונקציות חסומות בקטעים סופיים. אם הפונקציה לא חסומה ו/או הקטע לא חסום עדיין ניתן להגדיר "אינטגרל לא אמיתי" (improper integral). אינטגרלים של קטעים אינסופיים מהסוג 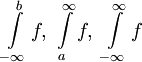 הם אינטגרלים לא אמיתיים מסוג 1.
הם אינטגרלים לא אמיתיים מסוג 1.
הגדרה: תהי f פונקציה מוגדרת בקטע מהסוג 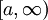 . נאמר ש-f אינטגרבילית מקומית (locally integrable) בקטע זה אם לכל
. נאמר ש-f אינטגרבילית מקומית (locally integrable) בקטע זה אם לכל 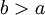 f אינטגרבילית בקטע
f אינטגרבילית בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
למשל, אם f רציפה למקוטעין אז היא אינטגרבילית מקומית.
הגדרה: תהי f מוגדרת ואינטגרבילית מקומית ב-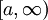 . נגדיר
. נגדיר 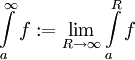 . אם הגבול קיים נאמר שהאינטגרל מתכנס, אחרת הוא מתבדר.
. אם הגבול קיים נאמר שהאינטגרל מתכנס, אחרת הוא מתבדר.
אינטגביליות מקומית מוגדרת באופן דומה עבור קטע מהצורה ![(-\infty,b]](/images/math/0/b/1/0b17dcebfc45d994217f05f19a1c9db8.png) ואם f אינטגרבילית מקומית שם נגדיר
ואם f אינטגרבילית מקומית שם נגדיר 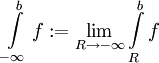 .
.
עבור f מוגדרת בכל  נאמר שהיא אינטגרבילית מקומית אם היא אינטגרבילית בכל קטע סופי, ואם כן נגדיר
נאמר שהיא אינטגרבילית מקומית אם היא אינטגרבילית בכל קטע סופי, ואם כן נגדיר 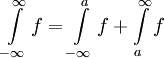 עבור
עבור 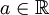 כרצוננו עבורו שני האינטגרלים באגף ימין מתכנסים.
כרצוננו עבורו שני האינטגרלים באגף ימין מתכנסים.
דוגמאות
-
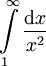 . נחשב: ניתן גם לכתוב בקיצור:
. נחשב: ניתן גם לכתוב בקיצור:![\begin{align}\int&=\lim_{R\to\infty}\int\limits_1^R\frac{\mathrm dx}{x^2}\\&=\lim_{R\to\infty}\left[-\frac1x\right]_{x=1}^R\\&=\lim_{R\to\infty}\left(-\frac1R+1\right)\\&=1\end{align}](/images/math/6/8/6/686b5229cf291132ec6db3ac1d06de5a.png)
![\int\limits_1^\infty\frac{\mathrm dx}{x^2}=\left[-\frac1x\right]_{x=1}^\infty=0-(-1)=1](/images/math/d/9/c/d9c19fa51b63ab623559a2c3966475e4.png) .
. -
![\int\limits_1^\infty\frac{\mathrm dx}x=[\ln|x|]_{x=1}^\infty=\ln(\infty)-0=\infty](/images/math/c/a/4/ca46449b6ad454b03e3bbf1a8aaefb9b.png) , כלומר האינטגרל מתבדר (אך מתכנס במובן הרחב).
, כלומר האינטגרל מתבדר (אך מתכנס במובן הרחב). - שאלה מארה"ב מלפני הרבה שנים: חצוצרה אינסופית תתקבל מסיבוב הגרף
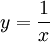 סביב ציר ה-x ב-
סביב ציר ה-x ב-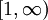 . האם יש מספיק צבע בעולם כדי לצבוע אותה מבפנים?
. האם יש מספיק צבע בעולם כדי לצבוע אותה מבפנים?
פתרון: לכאורה התשובה היא לא, כי שטח הפנים של החצוצרה הוא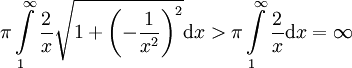 , כלומר אין מספיק צבע. אך מכיוון שכמות הצבע נמדדת ביחידות נפח ולא שטח, ומכיוון שהנפח בתוך החצוצרה הוא
, כלומר אין מספיק צבע. אך מכיוון שכמות הצבע נמדדת ביחידות נפח ולא שטח, ומכיוון שהנפח בתוך החצוצרה הוא 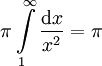 , יספיקו לנו
, יספיקו לנו 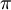 יחידות מעוקבות של צבע ואפילו ישאר לנו עודף.
יחידות מעוקבות של צבע ואפילו ישאר לנו עודף.
שאלה: האם התכנסות האינטגרל 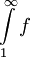 גוררת ש-
גוררת ש-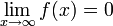 (בדומה לטורים)?
(בדומה לטורים)?
תשובה: לא. נגדיר פונקציה f שהגרף שלה הוא

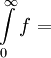 השטח שמתחת לגרף
השטח שמתחת לגרף 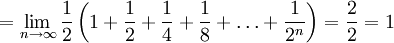
כלומר האינטגרל מתכנס, אבל 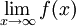 לא קיים.
לא קיים.