הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - תרגול/3.4.11"
(←פתרון) |
|||
| (5 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
=שימושי האינטגרל= | =שימושי האינטגרל= | ||
==דוגמה 1== | ==דוגמה 1== | ||
| − | חשבו את השטח הכלוא ע"י הפרבולה <math>y=4x</math> והישר <math>y=2x-4</math>. | + | חשבו את השטח הכלוא ע"י הפרבולה <math>y^2=4x</math> והישר <math>y=2x-4</math>. |
===פתרון=== | ===פתרון=== | ||
נצייר את הגרף (1) של הפונקציות ונמצא את 2 נקודות החיתוך: <math>(2x-4)^2=4x\implies x^2-5x+4=0\implies x=1,4</math>. | נצייר את הגרף (1) של הפונקציות ונמצא את 2 נקודות החיתוך: <math>(2x-4)^2=4x\implies x^2-5x+4=0\implies x=1,4</math>. | ||
| שורה 22: | שורה 22: | ||
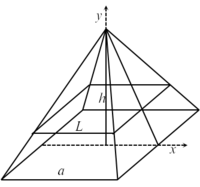
<div style="float:left;">[[קובץ:חישוב נפח פירמידה עם משולש.png|200px]]</div> | <div style="float:left;">[[קובץ:חישוב נפח פירמידה עם משולש.png|200px]]</div> | ||
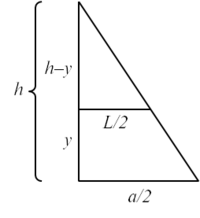
נבחר את מערכת הצירים כך שקודקוד הפירמידה עובר דרך ציר ה-y וציר ה-y מאונך לבסיסה. יוצא שציר ה-x מונח במישור על בסיס הפירמידה ומקביל/מאונך לצלעותיו. לכל קטע מהצורה <math>[0,y]</math> החתך הניצב לציר ה-y הוא ריבוע. נסמן ב-L את אורך הצלע של ריבוע זה. | נבחר את מערכת הצירים כך שקודקוד הפירמידה עובר דרך ציר ה-y וציר ה-y מאונך לבסיסה. יוצא שציר ה-x מונח במישור על בסיס הפירמידה ומקביל/מאונך לצלעותיו. לכל קטע מהצורה <math>[0,y]</math> החתך הניצב לציר ה-y הוא ריבוע. נסמן ב-L את אורך הצלע של ריבוע זה. | ||
| − | מדמיון משושלים נקבל <math>\frac{L/2}{a/2}=\frac{h-y}h\implies L=\frac{h-y}h\cdot a</math> ולכן שטח חתך כזה הוא <math>S(L)=\left(\frac{h-y}h\cdot a\right)^2</math>. נזכור שהחתך נפרס לרוחב, כלומר | + | מדמיון משושלים נקבל <math>\frac{L/2}{a/2}=\frac{h-y}h\implies L=\frac{h-y}h\cdot a</math> ולכן שטח חתך כזה הוא <math>S(L)=\left(\frac{h-y}h\cdot a\right)^2</math>. נזכור שהחתך נפרס לרוחב, כלומר המשתנה שלנו הוא y, וידוע שהוא רץ בין 0 ל-h. אם נקח לכל חתך כזה תיבה שבסיסה הוא החתך וגובהה שואף ל-0 ונחבר את נפחי התיבות נקבל את נפח הפירמידה. לכן הנפח הוא <math>\int\limits_0^h S(L)\mathrm dy=\int\limits_0^h\frac{(y-h)^2}{h^2}\cdot a^2\mathrm dy=\frac{a^2}{h^2}\left[\frac{(y-h)^3}3\right]_{y=0}^h=\frac{a^2h}3</math>. |
==נפח גוף סיבוב== | ==נפח גוף סיבוב== | ||
גרסה אחרונה מ־19:30, 15 במאי 2011
תוכן עניינים
שימושי האינטגרל
דוגמה 1
חשבו את השטח הכלוא ע"י הפרבולה 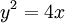 והישר
והישר 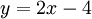 .
.
פתרון
נצייר את הגרף (1) של הפונקציות ונמצא את 2 נקודות החיתוך: 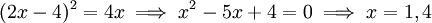 .
.
- דרך 1: נסובב את מערכת הצירים ב-
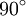 ונקבל גרף (2). עתה נחשב את השטח בין
ונקבל גרף (2). עתה נחשב את השטח בין 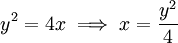 וכן
וכן 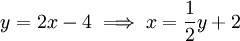 . קל לראות שהישר מעל הפרבולה, אבל גם אם לא כך אז הסימן של התוצאה יהא הפוך. לכן ניקח ערך מוחלט. שיעורי ה-y של נקודות החיתוך הם
. קל לראות שהישר מעל הפרבולה, אבל גם אם לא כך אז הסימן של התוצאה יהא הפוך. לכן ניקח ערך מוחלט. שיעורי ה-y של נקודות החיתוך הם 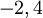 (לפי שיעורי ה-x) ולכן השטח הוא
(לפי שיעורי ה-x) ולכן השטח הוא ![\left|\int\limits_{-2}^4\left(\frac y2+2-\frac{y^2}4\right)\mathrm dy\right|=\left|\left[\frac{y^2}4+2y-\frac{y^3}{12}\right]_{y=-2}^4\right|=9](/images/math/b/f/a/bfa85122d17c471d588541649128f7cc.png) .
. - דרך 2: נפרק לשלושה שטחים: השטח
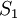 בין
בין 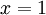 ל-4 ושני שטחים שווים
ל-4 ושני שטחים שווים 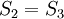 בין 0 ל-1, שטח אחד מעל ציר ה-x והשני מתחת. לפיכך השטח הכולל הוא
בין 0 ל-1, שטח אחד מעל ציר ה-x והשני מתחת. לפיכך השטח הכולל הוא 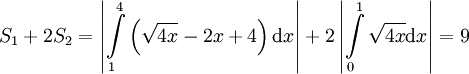
דוגמה 2
חשבו את השטח הכלוא בין הגרפים של הפונקציות 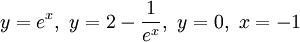 .
.
פתרון
נקודות חיתוך:
-
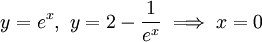
-
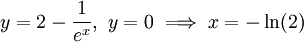
- ברור כי ל-
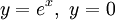 אין נקודת חיתוך.
אין נקודת חיתוך.
לכן השטח הוא 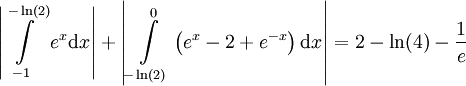 .
.
דוגמה 3
מצאו נוסחה לחישוב נפח של פירמידה ישרה אשר גובהה h ובסיסה ריבוע שאורך צלעו a.
פתרון
נבחר את מערכת הצירים כך שקודקוד הפירמידה עובר דרך ציר ה-y וציר ה-y מאונך לבסיסה. יוצא שציר ה-x מונח במישור על בסיס הפירמידה ומקביל/מאונך לצלעותיו. לכל קטע מהצורה ![[0,y]](/images/math/8/e/8/8e8f4f0ab7c865463148a7c347a08db9.png) החתך הניצב לציר ה-y הוא ריבוע. נסמן ב-L את אורך הצלע של ריבוע זה.
מדמיון משושלים נקבל
החתך הניצב לציר ה-y הוא ריבוע. נסמן ב-L את אורך הצלע של ריבוע זה.
מדמיון משושלים נקבל 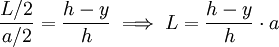 ולכן שטח חתך כזה הוא
ולכן שטח חתך כזה הוא 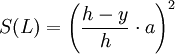 . נזכור שהחתך נפרס לרוחב, כלומר המשתנה שלנו הוא y, וידוע שהוא רץ בין 0 ל-h. אם נקח לכל חתך כזה תיבה שבסיסה הוא החתך וגובהה שואף ל-0 ונחבר את נפחי התיבות נקבל את נפח הפירמידה. לכן הנפח הוא
. נזכור שהחתך נפרס לרוחב, כלומר המשתנה שלנו הוא y, וידוע שהוא רץ בין 0 ל-h. אם נקח לכל חתך כזה תיבה שבסיסה הוא החתך וגובהה שואף ל-0 ונחבר את נפחי התיבות נקבל את נפח הפירמידה. לכן הנפח הוא ![\int\limits_0^h S(L)\mathrm dy=\int\limits_0^h\frac{(y-h)^2}{h^2}\cdot a^2\mathrm dy=\frac{a^2}{h^2}\left[\frac{(y-h)^3}3\right]_{y=0}^h=\frac{a^2h}3](/images/math/6/d/2/6d2381b3a16f4e4a900f7be68217db85.png) .
.
נפח גוף סיבוב
נפח גוף סיבוב סביב ציר ה-x מתקבל ע"י הנוסחה 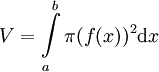 .
.
דוגמה 4
חשבו את הנפח הנוצר ע"י סיבוב הפרבולה 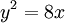 סביב ציר ה-x, עד לישר
סביב ציר ה-x, עד לישר 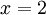 .
.
פתרון
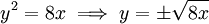 . מכיוון שעם סיבוב הרביע הראשון מתקבל הרביע הרביעי מספיק לחשב את נפח גוף הסיבוב של
. מכיוון שעם סיבוב הרביע הראשון מתקבל הרביע הרביעי מספיק לחשב את נפח גוף הסיבוב של 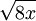 בין 0 ל-2. לכן, לפי הנוסחה,
בין 0 ל-2. לכן, לפי הנוסחה, ![V=\int\limits_0^2\pi\left(\sqrt{8x}\right)^2\mathrm dx=8\pi\left[\frac{x^2}2\right]_{x=0}^2=16\pi](/images/math/0/4/c/04c0849d4bed2bc6469d3e3c211f89f2.png) .
.
דוגמה 5
מצאו נוחה לחישוב נפח של כדור שרדיוסו r.
פתרון
ע"מ לחשב את הנוסחה נוכל לסובב את חציו העליון של עיגול. לפי נוסחת מעגל 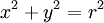 ולכן בחצי המישור העליון
ולכן בחצי המישור העליון 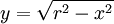 . הנפח הוא
. הנפח הוא 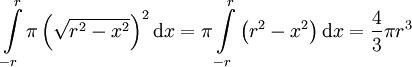 .
.
דוגמה 6
מצאו את נפח הגוף שנוצר כאשר מסובבים את התחום הכלוא בין הגרפים 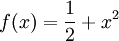 ו-
ו-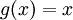 בקטע
בקטע ![[0,2]](/images/math/7/0/f/70fd3f388413505934da60b43afc4088.png) .
.
פתרון
נמצא את שיעורי ה-x של נקודות החיתוך: 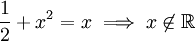 , כלומר אין נקודות חיתוך. לפיכך הנפח הוא
, כלומר אין נקודות חיתוך. לפיכך הנפח הוא 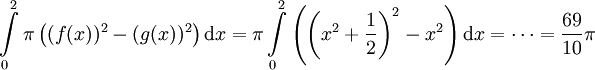 .
.
נפח גוף סיבוב המסתובב סביב ציר ה-y במקום ציר ה-x בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נתון ע"י הנוסחה
נתון ע"י הנוסחה 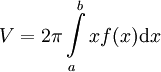 .
.
דוגמה 7
חשבו הנפח הנוצר מסיבוב התחום הנקבע ע"י 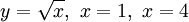 סביב ציר ה-y.
סביב ציר ה-y.
פתרון
לפי הנוסחה ![V=2\pi\int\limits_1^4\sqrt x^3\mathrm dx=2\pi\left[\frac{x^{5/2}}{5/2}\right]_{x=1}^4=\frac{124}5\pi](/images/math/a/3/6/a368bf6c85c948947893881e9b6c667c.png) .
.
דוגמה 8
חשב את נפח התחום שמתחת ל-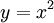 בקטע
בקטע ![[0,2]](/images/math/7/0/f/70fd3f388413505934da60b43afc4088.png) המסתובב סביב ציר ה-x.
המסתובב סביב ציר ה-x.
פתרון
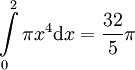 .
.