הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/6"
(←צירופים לינאריים - דוגמאות נוספות) |
אחיה בר-און (שיחה | תרומות) (←תרגיל) |
||
| (51 גרסאות ביניים של 8 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
[[88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול|חזרה למערכי התרגול]] | [[88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול|חזרה למערכי התרגול]] | ||
| − | |||
| − | + | ==משפט המימדים== | |
| + | [[משפט המימדים]]: | ||
| − | + | יהי <math>V</math> מ"ו ויהיו <math>U,W\leq V</math> תתי מרחבים. אזי | |
| + | <math>dim(U+W)=dim(U)+dim(W)-dim(U\cap W)</math> | ||
| − | ''' | + | ====סקיצה של ההוכחה - לא מפחיד כמו שנהוג לחשוב==== |
| + | #ניקח בסיס לU חיתוך W. נסמן אותו ב<math>\{v_1,...,v_k\}</math> | ||
| + | #נשלים אותו לבסיס לU. נסמן <math>\{v_1,...,v_k,u_1,...,u_m\}</math> | ||
| + | #נשלים את הבסיס לחיתוך גם לבסיס לW. נסמן <math>\{v_1,...,v_k,w_1,...,w_p\}</math> | ||
| + | #'''נוכיח''' (וזה עיקר העבודה) שהקבוצה <math>\{v_1,...,v_k,u_1,...,u_m,w_1,...,w_p\}</math> הינה בסיס לU+W: | ||
| + | ##נראה כי כל וקטור מהצורה u+w ניתן להצגה כצירוף לינארי של איברים אלה (זה ברור) | ||
| + | ##נראה כי הקבוצה הזו בת"ל, אחרת וקטורים שהנחנו שאינם בחיתוך יהיו חייבים להיות בחיתוך בסתירה | ||
| + | #המשל נובע בקלות מספירת הוקטורים בבסיסים שכן <math>dim(U+W) = k+m+p=(k+m)+(k+p) -k</math> | ||
| − | <math> | + | ===תרגיל 8.3=== |
| + | יהא V מ"ו ממימד 5, ויהיו U ממימד 3 ו-W ממימד 4 תתי מרחבים של V. מהן האפשרויות עבור <math>dim(U\cap W)</math>? הוכח! | ||
| − | <math>( | + | ====פתרון==== |
| + | ראשית, <math>U+W\subseteq V</math> ולכן <math>dim(U+W)\leq dim(V)=5</math>. אבל לפי משפט המימדים מתקיים <math>5\geq dim(U+W)=dim(U)+dim(W)-dim(U\cap W)=3+4-dim(U\cap W)</math>. | ||
| − | |||
| − | <math> | + | ביחד מקבלים ש <math>dim(U\cap W)\geq 2</math>. מצד שני, החיתוך מוכל גם בU וגם בW ולכן המימד שלו קטן שווה מהמימדים שלהם, ובפרט מהקטן מהם. לכן <math>dim(U\cap W)\leq 3</math>. |
| − | |||
| + | סה"כ האפשרויות למימד הן 2,3. קל למצוא דוגמאות המוכיחות שאפשרויות אלה אכן מתקבלות מתישהו. | ||
| + | ===תרגיל 8.5=== | ||
| + | יהא <math>V</math> מ"ו ממימד <math>n</math>, ויהיו <math>U,W</math> תתי מרחבים כך ש <math>dimU=n-1</math> ו-<math>W</math> אינו מוכל בU. הוכח כי <math>W+U=V</math> | ||
| − | + | ====הוכחה==== | |
| + | נוכיח בעזרת משפט המימדים ש <math>dim(U+W)=dimV</math> ואז המשל נובע (כי תת מרחב שמוכל בתת מרחב אחר מאותו מימד). | ||
| − | + | <math>dim(U+W)=dimU+dimW-dim(U\cap W)</math>. מכיוון שW אינו מוכל בU החיתוך בינהם שונה מW. ולכן <math>dim(U\cap W)<dimW </math> ולכן <math>dimW-dim(U\cap W)\geq 1</math>. ביחד מקבלים <math>dim(U+W)=n-1 + dimW -dim(U\cap W)\geq n-1+1=n=dimV</math>. משל. | |
| − | + | ===תרגיל=== | |
| − | + | יהיו W1,W2 ת"מ של מ"ו V כך ש <math>dim(W_1+W_2)=\dim (W_1\cap W_2) +1</math>. הוכיחו כי <math>\{W_1,W_2\}=\{W_1+W_2,W_1\cap W_2\}</math> | |
| + | פתרון: | ||
| + | מתקיים לפי נתון כי<math>\dim (W_1\cap W_2)\leq \dim W_1, \dim W_2 \leq dim(W_1+W_2)=\dim (W_1\cap W_2) +1</math> | ||
| + | ולכן לכל i מתקיים כי <math>\dim W_i </math> שווה למימד הסכום או למימד החיתוך. כיוון שיש הכלה <math>W_1\cap W_2\subseteq W_1,W_2\subseteq W_1+W_2 </math> אז יתקיים שיוויון. | ||
| + | כעת לא ייתכן כי <math>W_1,W_2</math> שניהם שווים כי אז מימד הסכום היה שווה למימד החיתוך. | ||
| + | |||
| + | === תרגיל === | ||
| + | יהא <math>V</math> מ"ו מימד אי זוגי <math>\dim V=2n+1</math> ויהיו <math>W_{1},W_{2},U_{1},U_{2}</math> ת"מ המקיימים כי <math>W_{1}+W_{2}=V=U_{1}+U_{2}</math> הוכיחו <math>\left(W_{1}\cap U_{1}\right)+\left(W_{1}\cap U_{2}\right)+\left(W_{2}\cap U_{1}\right)+\left(W_{2}\cap U_{2}\right)\neq\left\{ 0\right\}</math> | ||
| − | + | ==קואורדינטות== | |
| + | משפט: יהא <math>V</math> מ"ו מעל שדה <math>\mathbb{F}</math>, יהי <math>B=\{v_1,...,v_n\}</math> בסיס ל-<math>V</math> ויהי <math>v\in V</math> וקטור. | ||
| + | ראינו ש-<math>v</math> ניתן להצגה יחידה כצ"ל של <math>B</math> וההצגה שלו לפי הבסיס הוא וקטור שמורכב מהמקדמים של הצ"ל. | ||
| + | באופן פורמאלי, ההצגה של <math>v</math> לפי בסיס <math>B</math> הוא '''וקטור הקואורדינטות''' המסומן <math>[v]_B\in\mathbb{F}^n</math> ומוגדר להיות <math>[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}</math> כאשר <math>v=a_1v_1+...+a_nv_n</math>. | ||
| + | '''חשוב לזכור''' <math>[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}</math> אם"ם <math>v=a_1v_1+...+a_nv_n</math> | ||
| − | + | תרגיל: הוכח כי לכל בסיס <math>B</math> מתקיים | |
| − | + | <math>v=0</math> אם"ם <math>[v]_B=0</math>. | |
| + | |||
| + | הוכחה: ישירות מההגדרה. <math>B</math> בת"ל ולכן הצ"ל היחידי שמתאפס זהו הצ"ל הטריאלי. | ||
| − | + | בהכללה: | |
| − | <math> | + | <math>[v_1]_B=[v_2]_B</math> אמ"מ <math>v_1=v_2</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | + | הערה: במרחבים הוקטוריים שאנו נעבוד איתם יש '''בסיסים סטנדרטיים'''. הייחוד של הבסיסים הסטנדרטיים הוא שקל מאד לחשב קואורדינטות לפיהם. נסתכל במרחבים וקטורים ובבסיסים הסטנדרטיים שלהם: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | + | {| border="1" align="center" style="text-align:center;" | |
| + | |מרחב וקטורי | ||
| + | |בסיס סטנדרטי | ||
| + | |- | ||
| + | |<math>\mathbb{F}^n</math> | ||
| + | |<math>(1,0,...,0),(0,1,0,...,0),...,(0,...,0,1)</math> | ||
| + | |- | ||
| + | |<math>\mathbb{F}^{m\times n}</math> | ||
| + | |<math> | ||
| + | \begin{pmatrix}1 & 0 & \cdots & 0 \\ 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & 0\end{pmatrix}, | ||
| + | \begin{pmatrix}0 & 1 & \cdots & 0 \\ 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & 0\end{pmatrix},..., | ||
| + | \begin{pmatrix}0 & \cdots & \cdots & 0 \\ 1 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & 0\end{pmatrix},..., | ||
| + | \begin{pmatrix}0 & \cdots & \cdots & 0 \\ 0 & \cdots & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & 0 & 1 \end{pmatrix} | ||
| + | </math> | ||
| + | |- | ||
| + | |<math>\mathbb{F}_n[x]</math> | ||
| + | |<math>1,x,x^2,...,x^n</math> | ||
| + | |- | ||
| + | |} | ||
| − | + | '''דוגמא.''' | |
| + | חשב את הקואורדינטות של הוקטור <math>v=1+2x-x^2</math> לפי הבסיס הסטנדרטי S של <math>\mathbb{R}_3[x]</math>. למעשה הפולינום כמעט מוצג כצירוף לינארי של איברי הבסיס: | ||
| − | <math>\ | + | <math>v=a_1v_1+a_2v_2+a_3v_3+a_4v_4 = 1\cdot 1 + 2\cdot x + (-1)\cdot x^2 + 0\cdot x^3</math>. |
| − | + | ||
| − | + | ||
| − | \ | + | |
| + | לפיכך <math>[v]_S=(1,2,-1,0)</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''דוגמא.''' | |
| + | חשב את הקואורדינטות של הוקטור <math>(a,b,c)</math> לפי הבסיס הסטנדרטי S של <math>\mathbb{F}^n</math>. קל לראות ש <math>[v]_S = (a,b,c)</math>. | ||
| − | ''' | + | '''דוגמא.''' |
| + | <math>V=\mathbb{R}^2,B=\{(1,1),(1,-1)\}</math> מצא את הקואורדינטות של הוקטור <math> v=(a,b)</math> לפי הבסיס B. במקרה הכינותי מראש- | ||
| − | |||
| − | <math> | + | <math>v=\frac{a+b}{2}\cdot (1,1)+\frac{a-b}{2}\cdot (1,-1)</math> |
| − | |||
| + | ולכן לפי ההגדרה <math>[v]_B=(\frac{a+b}{2},\frac{a-b}{2})</math> | ||
| − | |||
| − | + | אנו רואים שאין זה קל למצוא את הקואורדינטות לפי בסיס כלשהו שאינו הסטנדרטי. | |
| − | + | === תרגיל === | |
| − | <math>\ | + | יהא <math>V</math> מ"ו מעל <math>\mathbb{F}</math> ויהי <math>B=\{v_1,\dots ,v_n\}</math> בסיס לו. יהיו <math>u_1,...,u_k\in V</math> וקטורים כלשהם וסקלארים <math>\alpha_i,\dots ,\alpha_k \in \mathbb{F}</math>. הוכח: |
| + | <math>\sum_{i=1}^k\alpha_i[u_i]_B =[\sum_{i=1}^k\alpha_iu_i]_B</math> | ||
| − | + | הוכחה: | |
| − | + | מ"ל את הטענה <math>[u_1]_B+[u_2]_B =[u_1+u_2]_B</math> ואת הטענה <math>\alpha[u_1]_B=[\alpha u_1]_B</math> (ואז המעבר לצ"ל כללי נעשה ע"י אינדוקציה) | |
| + | נסמן <math>u_1=a_1v_1+...+a_nv_n, u_2=b_1v_1+...+b_nv_n</math> אזי <math>u_1+u_2=(a_1+b_1)v_1+...+(a_n+b_n)v_n</math> ומתקיים | ||
| − | <math>\{ | + | <math>[u_1]_B+[u_2]_B =\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix} + \begin{pmatrix}b_1 \\ b_2 \\ \vdots \\ b_n\end{pmatrix} = |
| + | \begin{pmatrix}a_1+b_1 \\ a_2+b_2 \\ \vdots \\ a_n+b_n\end{pmatrix} | ||
| + | [u_1+u_2]_B</math> | ||
| − | = | + | בנוסף <math>\alpha u_1=\alpha a_1v_1+...+\alpha a_nv_n</math> ומתקיים |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <math>\alpha[u_1]_B= \alpha \begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}= | |
| − | + | \begin{pmatrix} \alpha_1 \\ \alpha a_2 \\ \vdots \\\alpha a_n\end{pmatrix} = | |
| − | + | [\alpha u_1]_B</math> | |
| − | + | ||
| + | מש"ל | ||
| − | ''' | + | '''מסקנה:''' |
| − | + | 2. <math>u_1,...,u_k</math> בת"ל אם"ם <math>[u_1]_B,...,[u_k]_B</math> בת"ל | |
| − | <math> | + | 3. <math>w\in span\{u_1,...,u_k\}</math> אם"ם <math>[w]_B\in span\{[u_1]_B,...,[u_k]_B\}</math> |
| − | + | ||
| − | + | הוכחה: | |
| − | + | ||
| − | + | 2. <math>u_1,...,u_k</math> בת"ל | |
| + | אמ"מ | ||
| − | + | <math>\sum_{i=1}^k\alpha_iu_i=0 \Rightarrow \forall i \; \alpha_i =0</math> | |
| − | + | אמ"מ | |
| + | <math>[\sum_{i=1}^k\alpha_iu_i]_B=[0]_B=0 \Rightarrow \forall i \; \alpha_i =0</math> | ||
| − | + | אמ"מ | |
| + | <math>\sum_{i=1}^k\alpha_i[u_i]_B=0 \Rightarrow \forall i \; \alpha_i =0</math> | ||
| − | + | אמ"מ | |
| − | + | ||
| − | + | <math>[u_1]_B,...,[u_k]_B</math> בת"ל | |
| − | + | ||
| − | + | 3. ברעיון דומה | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | מה בעצם המסקנה אומרת? שכל בדיקה/חישוב של תלות לינארית או פרישה '''בכל''' מרחב וקטורי (מטריצות, פולינומים, פונקציות) יכול בעצם להעשות במרחב הוקטורי המוכר והנוח <math>\mathbb{F}^n</math>. | |
| − | \begin{pmatrix} | + | |
| − | \begin{pmatrix} | + | ועוד הגדרה לפני ההמשך, עד כה דיברנו "רק" על ייצוג של וקטורים לפי בסיס. אפשר להכליל בפשטות לכל המרחב הוקטורי. הנה ההגדרה: |
| − | \begin{pmatrix} | + | |
| − | \begin{pmatrix}0 & | + | '''הגדרה''' : |
| + | יהא <math>V</math> מ"ו (או תת מרחב) ויהי <math>B</math> בסיס לו. אזי מרחב הקורדיאנטות (של <math>V</math> לפי בסיס <math>B</math>) הוא | ||
| + | |||
| + | <math>[V]_B = \{[v]_B \; | \; v\in V\}</math> | ||
| + | |||
| + | '''הערה :''' יהא <math>V</math> מ"ו, <math>W_1,W_2\leq V</math> תתי מרחבים ו <math>B</math> בסיס. אזי | ||
| + | #<math>[W_1 \cap W_2]_B = [W_1]_B \cap [W_2]_B</math> | ||
| + | #<math>[W_1 + W_2]_B = [W_1]_B + [W_2]_B</math> | ||
| + | |||
| + | == דוגמאות ואלגוריתמים== | ||
| + | === חיתוך תת מרחבים === | ||
| + | ===='''תרגיל 7.31''' ==== | ||
| + | |||
| + | נגדיר שני תתי מרחבים של <math>\mathbb{R}_3[x]</math>: | ||
| + | |||
| + | <math>V=\{p(x)|p(2)=0\}</math>, ו <math>U=\{p(x)|p(1)=0\}</math> | ||
| + | |||
| + | מצא את המימד של חיתוך המרחבים. | ||
| + | |||
| + | |||
| + | '''פתרון.''' | ||
| + | |||
| + | בתרגיל זה נשתמש בשיטה נפוצה ביותר. אנו מעוניינים לתאר את המרחבים הוקטוריים באופן קל יותר לעבודה מאשר התיאור לעיל; לכן ננסה לתאר את תתי המרחבים הללו כמרחבי פתרון של מערכת הומוגנית (אחת מהדרכים להצגת תת מרחב מתירגול קודם). המשתנים שלנו במערכת המשוואות יהיו '''המקדמים''' של הפולינומים. | ||
| + | |||
| + | נביט ב <math>V</math>. זהו אוסף כל הפולינומים ש2 הוא שורש שלהם. יהי פולינום כללי <math>p(x)=a+bx+cx^2+dx^3</math>, הוא שייך ל<math>V</math> אם"ם מקדמיו מקיימים את המשוואה הלינארית: <math>a+2b+4c+8d=0</math>. לכן <math>V=\{a+bx+cx^2+dx^3|a+2b+4c+8d=0\}</math> אם נעבוד עם הבסיס הסטנדרטי <math>S</math> נקבל כי | ||
| + | |||
| + | <math>[V]_S=\{\begin{pmatrix}a\\ b\\ c\\ d \end{pmatrix}\in \mathbb{R}^4 |a+2b+4c+8d=0\}</math> | ||
| + | |||
| + | באופן דומה הפולינום שייך ל<math>U</math> אם"ם מקדמיו מקיימים את המשוואה הלינארית <math>0=a+b+c+d</math>. ומרחב הקורדינאטות הוא | ||
| + | |||
| + | <math>[U]_S=\{\begin{pmatrix}a\\ b\\ c\\ d \end{pmatrix}\in \mathbb{R}^4 |a+b+c+d=0\}</math> | ||
| + | |||
| + | את החיתוך <math>[V]_S\cap[U]_S</math> קל למצוא! ראינו איך עושים זאת זה פשוט שווה ל | ||
| + | <math>\{\begin{pmatrix}a\\ b\\ c\\ d \end{pmatrix}\in \mathbb{R}^4 | | ||
| + | \begin{pmatrix} 1 & 2 & 4 & 8 \\ 1 & 1 & 1 & 1 \end{pmatrix} \begin{pmatrix}a\\ b\\ c\\ d \end{pmatrix} = 0 \}</math> | ||
| + | |||
| + | נדרג את המטריצה ונמצא את הפתרון: | ||
| + | |||
| + | <math>\begin{pmatrix} 1 & 2 & 4 & 8 \\ 1 & 1 & 1 & 1 \end{pmatrix} \to \begin{pmatrix} 1 & 2 & 4 & 8 \\ 0 & -1 & -3 & -7 \end{pmatrix} \to | ||
| + | \\ | ||
| + | \begin{pmatrix} 1 & 0 & -2 & -6 \\ 0 & -1 & -3 & -7 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & -2 & -6 \\ 0 & 1 & 3 & 7 \end{pmatrix} | ||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |||
| + | ולכן הפתרון הכללי הוא מהצורה <math>(2t+6s,-3t-7s,t,s)</math>, ולכן הבסיס הינו <math>(2,-3,1,0),(6,-7,0,1)</math>. | ||
| − | + | נחזור לצורה הפולינומית לקבל את התשובה הסופית: | |
| − | + | ||
| − | <math> | + | <math>U\cap V = sapn \{v_1, v_2 \; | \; [v_1]_s = (2,-3,1,0), [v_2]_s = (6,-7,0,1) \} = span\{2-3x+x^2,6-7x+x^3\}</math> |
| − | + | ====אלגוריתם למציאת חיתוך בין שני תתי מרחבים U,W==== | |
| + | ישנן שתי שיטות לחשב את החיתוך, נתחיל בראשונה (שביצענו הרגע, למעשה): | ||
| + | # החלף את <math>U,W</math> במרחב הקורדינאטות שלהם. | ||
| + | #מצא מערכת משוואות המתארת את <math>U</math> ומערכת משוואות המתארת את <math>W</math> | ||
| + | #פתור מערכת אחת המכילה את כל המשוואות משתי המערכות וקבל את החיתוך | ||
| + | # חזור ל <math>U,W</math> המקוריים. | ||
| + | שיטה שנייה: | ||
| + | # החלף את <math>U,W</math> במרחב הקורדינאטות שלהם. | ||
| + | # הצג את המרחבים כ <math>span(?)</math> | ||
| + | #כתוב צירוף לינארי כללי ב<math>U</math> וצירוף לינארי כללי ב<math>W</math> | ||
| + | #השווה את הצירופים ופתור מערכת משוואות על '''הסקלרים''' | ||
| + | #הצב את הסקלרים שקיבלת בצירוף הלינארי וקבל את החיתוך | ||
| + | # חזור ל <math>U,W</math> המקוריים. | ||
| − | |||
| − | |||
| − | + | =====תרגיל ====== | |
| − | + | ||
| + | מצא את החיתוך בין תתי המרחבים הבאים בשיטה השנייה לעיל. | ||
| − | <math> | + | <math>B=\operatorname{span}\left (\Big\{\begin{pmatrix} 1 & 0 \\ 0 & -1\end{pmatrix},\begin{pmatrix}0 & 1 \\ 0 & 0 \end{pmatrix},\begin{pmatrix}0 & 0 \\ 1 & 0\end{pmatrix}\Big\}\right ), |
| + | C=\operatorname{span}\left ( \Big\{\begin{pmatrix} 3 & 2 \\ 4 & -3\end{pmatrix},\begin{pmatrix}1 & 4 \\ -1 & 4 \end{pmatrix},\begin{pmatrix}1 & 1 \\ 1 & -2\end{pmatrix}\Big\}\right )</math> | ||
| − | + | '''פתרון.''' | |
| + | (קחו נשימה עמוקה) יהיו סקלרים a,b,c,x,y,z, וקטור הוא בחיתוך אם"ם הוא צירוף לינארי של שתי הקבוצות הפורשות: | ||
| − | + | <math>a\begin{pmatrix} 1 & 0 \\ 0 & -1\end{pmatrix}+b\begin{pmatrix}0 & 1 \\ 0 & 0 \end{pmatrix}+c\begin{pmatrix}0 & 0 \\ 1 & 0\end{pmatrix}=x\begin{pmatrix} 3 & 2 \\ 4 & -3\end{pmatrix}+y\begin{pmatrix}1 & 4 \\ -1 & 4 \end{pmatrix}+z\begin{pmatrix}1 & 1 \\ 1 & -2\end{pmatrix}</math> | |
| − | + | במרחב הקורדינאטות (עם הבסיס הסטדנדרטי <math>S</math>, נקבל את השיוון | |
| − | + | <math>a\begin{pmatrix} 1 \\ 0 \\ 0 \\ -1\end{pmatrix}+b\begin{pmatrix}0 \\ 1 \\ 0 \\ 0 \end{pmatrix}+c\begin{pmatrix}0 \\0 \\ 1 \\ 0\end{pmatrix}=x\begin{pmatrix} 3 \\ 2 \\ 4 \\ -3\end{pmatrix}+y\begin{pmatrix}1 \\ 4 \\ -1 \\ 4 \end{pmatrix}+z\begin{pmatrix}1\\ 1 \\ 1 \\ -2\end{pmatrix}</math> | |
| − | + | ||
| − | + | ||
| − | + | לכן מערכת המשוואות '''על הסקלרים''' הינה: | |
| + | <math>\begin{pmatrix} | ||
| + | 1 & 0 & 0 & -3 & -1 & -1 & | & 0 \\ | ||
| + | 0 & 1 & 0 & -2 & -4 & -1 & | & 0 \\ | ||
| + | 0 & 0 & 1 & -4 & 1 & -1 & | & 0 \\ | ||
| + | -1 & 0 & 0 & 3 & -4 & 2 & | & 0 \\ | ||
| + | \end{pmatrix}</math> | ||
| + | |||
| + | נדרג ונמצא את הפתרונות (שימו לב: מספיק למצוא רק את x,y,z או רק את a,b,c מכיוון שבהנתן צירוף לינארי של איברי C שנותן את החיתוך אין צורך להמשיך (כמו כן לגבי B).) | ||
| + | |||
| + | <math>\begin{pmatrix} | ||
| + | 1 & 0 & 0 & -3 & -1 & -1 & | & 0 \\ | ||
| + | 0 & 1 & 0 & -2 & -4 & -1 & | & 0 \\ | ||
| + | 0 & 0 & 1 & -4 & 1 & -1 & | & 0 \\ | ||
| + | 0 & 0 & 0 & 0 & -5 & 1 & | & 0 \\ | ||
| + | |||
| + | \end{pmatrix}</math> | ||
| + | |||
| + | במקרה זה קל יותר למצוא את x,y,z; המשתנים החופשיים הינם x,z ומתקיים z=5y. ולכן הצ"ל הכללי בחיתוך הינו: | ||
| + | |||
| + | <math>[B]_S \cap [C]_S= | ||
| + | \Big\{x\begin{pmatrix} 3 \\ 2 \\ 4 \\ -3\end{pmatrix}+y\begin{pmatrix}1 \\ 4 \\ -1 \\ 4 \end{pmatrix}+5y\begin{pmatrix}1 \\ 1 \\ 1 \\ -2\end{pmatrix}\Big\}= \\ | ||
| + | \Big\{x\begin{pmatrix} 3 \\ 2 \\ 4 \\ -3\end{pmatrix}+y\begin{pmatrix}6 \\ 9 \\ 4 \\ -6 \end{pmatrix}\Big\}= | ||
| + | span\Big\{\begin{pmatrix} 3 \\ 2 \\ 4 \\-3\end{pmatrix},\begin{pmatrix}6 \\ 9 \\ 4 \\ -6 \end{pmatrix}\Big\} | ||
| + | </math> | ||
| + | |||
| + | אם נחזור למרחבים המקוריים נקבל כי | ||
| + | |||
| + | <math>B\cap C=span\Big\{\begin{pmatrix} 3 & 2 \\ 4 & -3\end{pmatrix},\begin{pmatrix}6 & 9 \\ 4 & -6 \end{pmatrix}\Big\}</math> | ||
| + | |||
| + | === תלות לינארית === | ||
'''דוגמא.''' | '''דוגמא.''' | ||
האם הפולינומים <math>v_1=1+x^2,v_2=1-x,v_3=x+x^2</math> תלויים לינארית? | האם הפולינומים <math>v_1=1+x^2,v_2=1-x,v_3=x+x^2</math> תלויים לינארית? | ||
| − | דבר ראשון, נעבור למרחב הקואורדינטות. מכיוון שבחירת הבסיס היא לשיקולנו, נבחר את הבסיס הסטנדרטי S של הפולינומים איתו קל לעבוד. מתקיים ש <math>[v_1]_S=(1,0,1),[v_2]_S=(1,-1,0),[v_3]=(0,1,1)</math> | + | דבר ראשון, נעבור למרחב הקואורדינטות. מכיוון שבחירת הבסיס היא לשיקולנו, נבחר את הבסיס הסטנדרטי S של הפולינומים איתו קל לעבוד. מתקיים ש <math>[v_1]_S=(1,0,1),[v_2]_S=(1,-1,0),[v_3]_S=(0,1,1)</math> |
| − | הוכחנו בשיעור שעבר שוקטורים "רגילים" ת"ל אם"ם המטריצה שהם השורות שלה אינה הפיכה אם"ם הצורה המדורגת של המטריצה מכילה שורת אפסים. לכן, נשים את וקטורי הקואורדינטות בשורות מטריצה ונדרג. | + | הוכחנו בשיעור שעבר שוקטורים "רגילים" ת"ל אם"ם המטריצה שהם השורות שלה אינה הפיכה אם"ם הצורה המדורגת של המטריצה מכילה שורת אפסים. לכן, נשים את וקטורי הקואורדינטות בשורות מטריצה ונדרג. |
| − | <math>\begin{pmatrix}1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 1 & 1\end{pmatrix}</math> | + | <math> |
| + | \begin{pmatrix}1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 1 & 1\end{pmatrix} | ||
| + | \xrightarrow[]{R_3-R_1,R_3+R_2} | ||
| + | \begin{pmatrix}1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 0 & 0\end{pmatrix}</math> | ||
| − | |||
| − | <math>\begin{pmatrix}1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 0 & 0\end{pmatrix}</math> | + | לכן וקטורי הקואורדינטות תלויים לינארית ולכן הפולינומים עצמם תלויים לינארית. |
| + | |||
| + | |||
| + | דרך נוספת: נשים את הוקטורים בעמודה של מטריצה <math>A</math>. צ"ל של עמודות <math>A</math> זה פשוט <math>Ax</math>. ולכן הוקטורים בת"ל אמ"מ הפתרון היחידי למערכת <math>Ax=0</math> (צ"ל שמתאפס) הוא הפתרון הטריאלי (הצ"ל הטריאלי) | ||
| + | |||
| + | <math> | ||
| + | \begin{pmatrix}1 & 1 & 0 \\ 0 & -1 & 1 \\ 1 & 0 & 1\end{pmatrix} \to | ||
| + | \begin{pmatrix}1 & 1 & 0 \\ 0 & -1 & 1 \\ 0 & -1 & 1\end{pmatrix} \to | ||
| + | \begin{pmatrix}1 & 1 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & 0\end{pmatrix} \ | ||
| + | </math> | ||
| + | |||
| + | קיבלנו שיש משתנים חופשיים ולכן יש פתרון לא טרויאלי ולכן הוקטורים תלויים לינארית! | ||
| − | + | נסכם את התהליך: | |
| − | ===אלגוריתם לבדיקת תלות לינארית בין וקטורים=== | + | ====אלגוריתם לבדיקת תלות לינארית בין וקטורים==== |
#הפוך את הוקטורים לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים | #הפוך את הוקטורים לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים | ||
#שים את וקטורי הקואורדינטות ב'''שורות''' מטריצה A | #שים את וקטורי הקואורדינטות ב'''שורות''' מטריצה A | ||
| שורה 209: | שורה 326: | ||
#אם הגעת לצורה מדורגת ללא שורת אפסים סימן שהוקטורים בלתי תלויים לינארית | #אם הגעת לצורה מדורגת ללא שורת אפסים סימן שהוקטורים בלתי תלויים לינארית | ||
| + | ובדרך הנוספת | ||
| + | #הפוך את הוקטורים לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים | ||
| + | #שים את וקטורי הקואורדינטות ב'''עמודות''' מטריצה A | ||
| + | # בדוק אם יש פתרון לא טריאלי למערכת <math>Ax=0</math> | ||
| + | # אם יש אז הם תלויים ואם אין אז הם בת"ל | ||
| + | === צירופים לינאריים === | ||
'''דוגמא.''' | '''דוגמא.''' | ||
| − | האם המטריצה <math>v=\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix}</math> | + | האם המטריצה <math>v=\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix}</math> היא צ"ל של המטריצות |
<math> | <math> | ||
v_1=\begin{pmatrix}1 & 1 \\ 0 & 0\end{pmatrix}, | v_1=\begin{pmatrix}1 & 1 \\ 0 & 0\end{pmatrix}, | ||
v_2=\begin{pmatrix}1 & 0 \\ 2 & 1\end{pmatrix}, | v_2=\begin{pmatrix}1 & 0 \\ 2 & 1\end{pmatrix}, | ||
v_3=\begin{pmatrix}2 & 2 \\ 10 & 10\end{pmatrix} | v_3=\begin{pmatrix}2 & 2 \\ 10 & 10\end{pmatrix} | ||
| − | </math> | + | </math>? |
| − | ? אם כן, הצג אותה כצירוף לינארי שלהן. | + | אם כן, הצג אותה כצירוף לינארי שלהן. |
פתרון: נעבור דבר ראשון למרחב הקואורדינטות לפי הבסיס הסטנדרטי <math>S=\Big\{\begin{pmatrix}1 & 0 \\ 0 & 0\end{pmatrix},\begin{pmatrix}0 & 1 \\ 0 & 0\end{pmatrix},\begin{pmatrix}0 & 0 \\ 1 & 0\end{pmatrix},\begin{pmatrix}0 & 0 \\ 0 & 1\end{pmatrix}\Big\}</math> | פתרון: נעבור דבר ראשון למרחב הקואורדינטות לפי הבסיס הסטנדרטי <math>S=\Big\{\begin{pmatrix}1 & 0 \\ 0 & 0\end{pmatrix},\begin{pmatrix}0 & 1 \\ 0 & 0\end{pmatrix},\begin{pmatrix}0 & 0 \\ 1 & 0\end{pmatrix},\begin{pmatrix}0 & 0 \\ 0 & 1\end{pmatrix}\Big\}</math> | ||
| שורה 224: | שורה 347: | ||
| − | למדנו בשיעור שעבר שוקטור b נפרש על ידי וקטורים מסויימים אם"ם קיים פתרון למערכת Ax=b כאשר A היא המטריצה שעמודותיה הם אותם וקטורים. הפתרון x הוא | + | למדנו בשיעור שעבר שוקטור b נפרש על ידי וקטורים מסויימים אם"ם קיים פתרון למערכת Ax=b כאשר A היא המטריצה שעמודותיה הם אותם וקטורים. הפתרון x הוא וקטור הסקלרים מהצירוף הלינארי. לכן, אנו רוצים לדעת האם קיים פתרון למערכת ואם כן מהו: |
<math>\begin{pmatrix}1 & 1 & 2\\ 1 & 0 & 2\\ 0 & 2 & 10\\ 0 & 1 & 10\end{pmatrix} x = \begin{pmatrix}1 \\ 2 \\ 3 \\4 \end{pmatrix}</math> | <math>\begin{pmatrix}1 & 1 & 2\\ 1 & 0 & 2\\ 0 & 2 & 10\\ 0 & 1 & 10\end{pmatrix} x = \begin{pmatrix}1 \\ 2 \\ 3 \\4 \end{pmatrix}</math> | ||
| שורה 233: | שורה 356: | ||
נסכם: | נסכם: | ||
| − | ===אלגוריתם לחישוב צירוף לינארי=== | + | ====אלגוריתם לחישוב צירוף לינארי==== |
#נתון וקטור b וקבוצת וקטורים. העבר את כולם לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים | #נתון וקטור b וקבוצת וקטורים. העבר את כולם לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים | ||
#פתור את המערכת Ax=b כאשר '''עמודות''' A הינן וקטורי הקואורדינטות של קבוצת הוקטורים הפורשים | #פתור את המערכת Ax=b כאשר '''עמודות''' A הינן וקטורי הקואורדינטות של קבוצת הוקטורים הפורשים | ||
| שורה 239: | שורה 362: | ||
#אם קיים פתרון x אזי הוא מכיל את הסקלרים של הצירוף הלינארי בהתאם לסדר העמודות בA | #אם קיים פתרון x אזי הוא מכיל את הסקלרים של הצירוף הלינארי בהתאם לסדר העמודות בA | ||
| − | == | + | ==מטריצות מעבר בין בסיסים== |
| − | + | ראינו שקל מאד למצוא קואורדינטות לפי הבסיס הסטנדרטי, נשתמש בהנחה הזו בהמשך. אנו מעוניינים לדעת כיצד לחשב קואורדינטות לפי בסיס כלשהו, לאו דווקא סטנדרטי. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | '''משפט:''' | + | '''משפט:''' יהא <math>V</math> מ"ו ויהיו <math>E,F</math> בסיסים לו. אזי '''קיימת''' מטריצה '''יחידה''' המסומנת <math>[I]^E_F</math> המקיימת את הפסוק הבא: |
| + | <math>\forall v\in V: [I]^E_F[v]_E=[v]_F</math> | ||
| − | |||
| − | + | נסמן <math>E=\{v_1,...,v_n\}</math> ו <math>F=\{w_1,...,w_n\}</math>. אזי מתקיים ש<math>[I]^E_F</math> הינה המטריצה שעמודותיה הן <math>[v_i]_F</math> | |
'''דוגמא.''' | '''דוגמא.''' | ||
| − | + | יהא <math>V=\mathbb{R}^2</math> ושני בסיסים | |
| + | <math>E=\{v_1=\begin{pmatrix} 3\\ -2 \end{pmatrix} , v_2 = \begin{pmatrix} 0\\ 1 \end{pmatrix} \}</math> | ||
| + | ו<math>F=\{w_1= \begin{pmatrix} 1\\ 0 \end{pmatrix},w_2 = \begin{pmatrix} 1\\ 1 \end{pmatrix}\}</math> | ||
| − | + | נמצא את <math>[I]^E_F</math>. | |
| − | <math>\ | + | מתקיים כי |
| + | <math> | ||
| + | v_1 = \mathbf{5}w_1-\mathbf{2}w_2 \\ | ||
| + | v_2 = -\mathbf{1}w_1+\mathbf{1}w_2 | ||
| + | </math> | ||
| − | + | לכן | |
| − | + | ||
| − | + | ||
| − | + | <math> | |
| + | [I]^E_F= | ||
| + | \begin{pmatrix} 5& -1 \\ -2 & 1 \end{pmatrix} | ||
| + | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''תרגיל:''' |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
הוכח ש <math>[I]^S_B[I]^A_S=[I]^A_B</math>. מכיוון שאנו יודעים שמטריצה המעבר הינה יחידה, מספיק להראות שהכפל מקיים את הפסוק מההגדרה: | הוכח ש <math>[I]^S_B[I]^A_S=[I]^A_B</math>. מכיוון שאנו יודעים שמטריצה המעבר הינה יחידה, מספיק להראות שהכפל מקיים את הפסוק מההגדרה: | ||
| שורה 311: | שורה 413: | ||
#הפוך את המטריצה האחרונה לקבל <math>([I]^F_S)^{-1}=[I]^S_F</math> | #הפוך את המטריצה האחרונה לקבל <math>([I]^F_S)^{-1}=[I]^S_F</math> | ||
#כפול את המטריצות על מנת לקבל את התוצאה הסופית <math>[I]^S_F[I]^E_S=[I]^E_F</math> | #כפול את המטריצות על מנת לקבל את התוצאה הסופית <math>[I]^S_F[I]^E_S=[I]^E_F</math> | ||
| + | |||
| + | |||
| + | ====דוגמא:==== | ||
| + | |||
| + | <math>V=\mathbb{R}_2[x]</math> מצא את <math>[I]^E_F</math> כאשר | ||
| + | |||
| + | <math>E=\{1+x, x+x^2, x^2\}, F=\{x,1+x,1+2x^2\}</math> | ||
| + | |||
| + | פתרון: | ||
| + | |||
| + | נסמן <math>S</math> הבסיס הסטנדרטי ואז | ||
| + | <math> | ||
| + | [I]^E_S= | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & 0 \\ | ||
| + | 1 & 1 & 0 \\ | ||
| + | 0 & 1 & 1 | ||
| + | \end{pmatrix}, | ||
| + | |||
| + | [I]^F_S= | ||
| + | \begin{pmatrix} | ||
| + | 0 & 1 & 1 \\ | ||
| + | 1 & 1 & 0 \\ | ||
| + | 0 & 0 & 2 | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | אחרי חישובים מקבלים כי | ||
| + | |||
| + | <math>[I]^S_F= | ||
| + | \begin{pmatrix} | ||
| + | 0 & 1 & 1 \\ | ||
| + | 1 & 1 & 0 \\ | ||
| + | 0 & 0 & 2 | ||
| + | \end{pmatrix}^{-1} = | ||
| + | |||
| + | |||
| + | \begin{pmatrix} | ||
| + | -1 & 1 & 0.5 \\ | ||
| + | 1 & 0 & -0.5 \\ | ||
| + | 0 & 0 & 0.5 | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | ולכן | ||
| + | |||
| + | <math>[I]^E_F=[I]^S_F[I]^E_S= | ||
| + | |||
| + | \begin{pmatrix} | ||
| + | -1 & 1 & 0.5 \\ | ||
| + | 1 & 0 & -0.5 \\ | ||
| + | 0 & 0 & 0.5 | ||
| + | \end{pmatrix} | ||
| + | |||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & 0 \\ | ||
| + | 1 & 1 & 0 \\ | ||
| + | 0 & 1 & 1 | ||
| + | \end{pmatrix} | ||
| + | = | ||
| + | |||
| + | \begin{pmatrix} | ||
| + | 0 & 1.5 & 0.5 \\ | ||
| + | 1 & -0.5 & -0.5 \\ | ||
| + | 0 & 0.5 & 0.5 | ||
| + | \end{pmatrix} | ||
| + | |||
| + | </math> | ||
| + | |||
| + | ====תרגיל==== | ||
| + | |||
| + | תהא | ||
| + | <math> | ||
| + | A = | ||
| + | \begin{pmatrix} | ||
| + | 1 & 2 & 3 \\ | ||
| + | 4 & 5 & 6 \\ | ||
| + | 1 & 1 & 0 \\ | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | ובסיס | ||
| + | |||
| + | <math> | ||
| + | E = | ||
| + | \{ | ||
| + | \begin{pmatrix} | ||
| + | 1 \\ | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | \end{pmatrix}, | ||
| + | \begin{pmatrix} | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | \end{pmatrix}, | ||
| + | \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | \end{pmatrix} | ||
| + | \} | ||
| + | </math> | ||
| + | |||
| + | מצאו בסיס <math>F</math> כך ש <math>A=[I]^E_F</math> | ||
| + | |||
| + | פתרון: | ||
| + | |||
| + | נסמן <math>F=\{v_1,v_2,v_3\}</math> | ||
| + | |||
| + | נחשב ונמצא כי | ||
| + | |||
| + | <math> | ||
| + | [I]^F_E= A^{-1} = | ||
| + | \begin{pmatrix} | ||
| + | -4/3 & 1/3 & 1 \\ | ||
| + | 2/3 & 1/3 & -2 \\ | ||
| + | 1/3 & -1/3 & 1 \\ | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | מהגדרה נקבל כי | ||
| + | |||
| + | <math> | ||
| + | v_1 = | ||
| + | -4/3 | ||
| + | \begin{pmatrix} | ||
| + | 1 \\ | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | \end{pmatrix}+ | ||
| + | 2/3 | ||
| + | \begin{pmatrix} | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | \end{pmatrix}+ | ||
| + | 1/3 | ||
| + | \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | \end{pmatrix} = | ||
| + | \begin{pmatrix} | ||
| + | -2/3 \\ | ||
| + | -4/3 \\ | ||
| + | 1 \\ | ||
| + | \end{pmatrix}, | ||
| + | |||
| + | \\ | ||
| + | v_2 = | ||
| + | 1/3 | ||
| + | \begin{pmatrix} | ||
| + | 1 \\ | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | \end{pmatrix}+ | ||
| + | 1/3 | ||
| + | \begin{pmatrix} | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | \end{pmatrix}+ | ||
| + | -1/3 | ||
| + | \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | \end{pmatrix} = | ||
| + | \begin{pmatrix} | ||
| + | 2/3 \\ | ||
| + | 1/3 \\ | ||
| + | 0 \\ | ||
| + | \end{pmatrix}, | ||
| + | \\ | ||
| + | v_3 = | ||
| + | 1 | ||
| + | \begin{pmatrix} | ||
| + | 1 \\ | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | \end{pmatrix}+ | ||
| + | -2 | ||
| + | \begin{pmatrix} | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | \end{pmatrix}+ | ||
| + | 1 | ||
| + | \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | \end{pmatrix} = | ||
| + | \begin{pmatrix} | ||
| + | -1 \\ | ||
| + | 1 \\ | ||
| + | -1 \\ | ||
| + | \end{pmatrix} | ||
| + | |||
| + | </math> | ||
גרסה אחרונה מ־13:27, 23 ביולי 2020
משפט המימדים
יהי  מ"ו ויהיו
מ"ו ויהיו 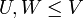 תתי מרחבים. אזי
תתי מרחבים. אזי
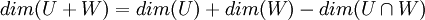
סקיצה של ההוכחה - לא מפחיד כמו שנהוג לחשוב
- ניקח בסיס לU חיתוך W. נסמן אותו ב
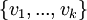
- נשלים אותו לבסיס לU. נסמן
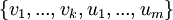
- נשלים את הבסיס לחיתוך גם לבסיס לW. נסמן
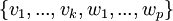
- נוכיח (וזה עיקר העבודה) שהקבוצה
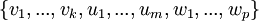 הינה בסיס לU+W:
הינה בסיס לU+W:
- נראה כי כל וקטור מהצורה u+w ניתן להצגה כצירוף לינארי של איברים אלה (זה ברור)
- נראה כי הקבוצה הזו בת"ל, אחרת וקטורים שהנחנו שאינם בחיתוך יהיו חייבים להיות בחיתוך בסתירה
- המשל נובע בקלות מספירת הוקטורים בבסיסים שכן
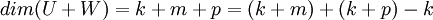
תרגיל 8.3
יהא V מ"ו ממימד 5, ויהיו U ממימד 3 ו-W ממימד 4 תתי מרחבים של V. מהן האפשרויות עבור  ? הוכח!
? הוכח!
פתרון
ראשית, 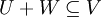 ולכן
ולכן 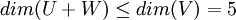 . אבל לפי משפט המימדים מתקיים
. אבל לפי משפט המימדים מתקיים 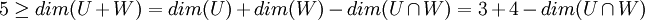 .
.
ביחד מקבלים ש 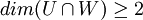 . מצד שני, החיתוך מוכל גם בU וגם בW ולכן המימד שלו קטן שווה מהמימדים שלהם, ובפרט מהקטן מהם. לכן
. מצד שני, החיתוך מוכל גם בU וגם בW ולכן המימד שלו קטן שווה מהמימדים שלהם, ובפרט מהקטן מהם. לכן 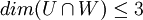 .
.
סה"כ האפשרויות למימד הן 2,3. קל למצוא דוגמאות המוכיחות שאפשרויות אלה אכן מתקבלות מתישהו.
תרגיל 8.5
יהא  מ"ו ממימד
מ"ו ממימד 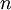 , ויהיו
, ויהיו 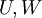 תתי מרחבים כך ש
תתי מרחבים כך ש 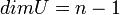 ו-
ו-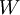 אינו מוכל בU. הוכח כי
אינו מוכל בU. הוכח כי 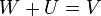
הוכחה
נוכיח בעזרת משפט המימדים ש 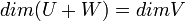 ואז המשל נובע (כי תת מרחב שמוכל בתת מרחב אחר מאותו מימד).
ואז המשל נובע (כי תת מרחב שמוכל בתת מרחב אחר מאותו מימד).
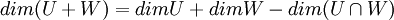 . מכיוון שW אינו מוכל בU החיתוך בינהם שונה מW. ולכן
. מכיוון שW אינו מוכל בU החיתוך בינהם שונה מW. ולכן 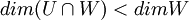 ולכן
ולכן 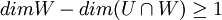 . ביחד מקבלים
. ביחד מקבלים 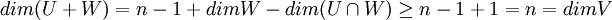 . משל.
. משל.
תרגיל
יהיו W1,W2 ת"מ של מ"ו V כך ש 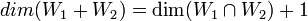 . הוכיחו כי
. הוכיחו כי 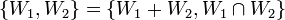
פתרון:
מתקיים לפי נתון כי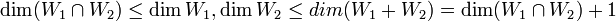 ולכן לכל i מתקיים כי
ולכן לכל i מתקיים כי 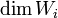 שווה למימד הסכום או למימד החיתוך. כיוון שיש הכלה
שווה למימד הסכום או למימד החיתוך. כיוון שיש הכלה 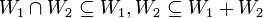 אז יתקיים שיוויון.
כעת לא ייתכן כי
אז יתקיים שיוויון.
כעת לא ייתכן כי 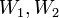 שניהם שווים כי אז מימד הסכום היה שווה למימד החיתוך.
שניהם שווים כי אז מימד הסכום היה שווה למימד החיתוך.
תרגיל
יהא  מ"ו מימד אי זוגי
מ"ו מימד אי זוגי 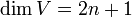 ויהיו
ויהיו 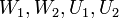 ת"מ המקיימים כי
ת"מ המקיימים כי 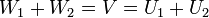 הוכיחו
הוכיחו 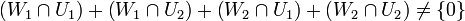
קואורדינטות
משפט: יהא  מ"ו מעל שדה
מ"ו מעל שדה  , יהי
, יהי 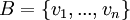 בסיס ל-
בסיס ל- ויהי
ויהי 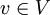 וקטור.
ראינו ש-
וקטור.
ראינו ש-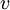 ניתן להצגה יחידה כצ"ל של
ניתן להצגה יחידה כצ"ל של  וההצגה שלו לפי הבסיס הוא וקטור שמורכב מהמקדמים של הצ"ל.
באופן פורמאלי, ההצגה של
וההצגה שלו לפי הבסיס הוא וקטור שמורכב מהמקדמים של הצ"ל.
באופן פורמאלי, ההצגה של 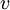 לפי בסיס
לפי בסיס  הוא וקטור הקואורדינטות המסומן
הוא וקטור הקואורדינטות המסומן ![[v]_B\in\mathbb{F}^n](/images/math/4/8/d/48d175f864d880e25a45feb85ad8c94e.png) ומוגדר להיות
ומוגדר להיות ![[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}](/images/math/f/9/5/f95c4d5b167fb4c2880885415ca0e149.png) כאשר
כאשר 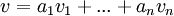 .
.
חשוב לזכור ![[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}](/images/math/f/9/5/f95c4d5b167fb4c2880885415ca0e149.png) אם"ם
אם"ם 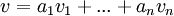
תרגיל: הוכח כי לכל בסיס  מתקיים
מתקיים
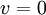 אם"ם
אם"ם ![[v]_B=0](/images/math/a/a/c/aac616b8c08680fd2fb1e1e5cccb8134.png) .
.
הוכחה: ישירות מההגדרה.  בת"ל ולכן הצ"ל היחידי שמתאפס זהו הצ"ל הטריאלי.
בת"ל ולכן הצ"ל היחידי שמתאפס זהו הצ"ל הטריאלי.
בהכללה:
![[v_1]_B=[v_2]_B](/images/math/e/c/1/ec117a8ef8974dc2db75d13479c273bb.png) אמ"מ
אמ"מ 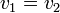
הערה: במרחבים הוקטוריים שאנו נעבוד איתם יש בסיסים סטנדרטיים. הייחוד של הבסיסים הסטנדרטיים הוא שקל מאד לחשב קואורדינטות לפיהם. נסתכל במרחבים וקטורים ובבסיסים הסטנדרטיים שלהם:
| מרחב וקטורי | בסיס סטנדרטי |
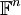
|
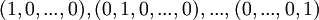
|
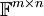
|

|
![\mathbb{F}_n[x]](/images/math/5/0/4/504c6115c35647a079e43b17f4468bef.png)
|
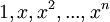
|
דוגמא.
חשב את הקואורדינטות של הוקטור 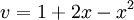 לפי הבסיס הסטנדרטי S של
לפי הבסיס הסטנדרטי S של ![\mathbb{R}_3[x]](/images/math/8/4/e/84ef8e18caf28275bb31fb78edc3a348.png) . למעשה הפולינום כמעט מוצג כצירוף לינארי של איברי הבסיס:
. למעשה הפולינום כמעט מוצג כצירוף לינארי של איברי הבסיס:
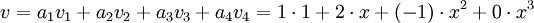 .
.
לפיכך ![[v]_S=(1,2,-1,0)](/images/math/7/2/c/72ce9c7c6545dbb68aececb179bddf8c.png) .
.
דוגמא.
חשב את הקואורדינטות של הוקטור 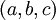 לפי הבסיס הסטנדרטי S של
לפי הבסיס הסטנדרטי S של 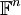 . קל לראות ש
. קל לראות ש ![[v]_S = (a,b,c)](/images/math/1/6/0/160aaa76dd5f1b407f9a424f38ca36ad.png) .
.
דוגמא.
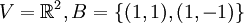 מצא את הקואורדינטות של הוקטור
מצא את הקואורדינטות של הוקטור 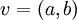 לפי הבסיס B. במקרה הכינותי מראש-
לפי הבסיס B. במקרה הכינותי מראש-
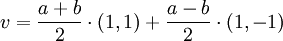
ולכן לפי ההגדרה ![[v]_B=(\frac{a+b}{2},\frac{a-b}{2})](/images/math/0/b/f/0bfb2b0112942154b05f33bb27cc4e3b.png)
אנו רואים שאין זה קל למצוא את הקואורדינטות לפי בסיס כלשהו שאינו הסטנדרטי.
תרגיל
יהא  מ"ו מעל
מ"ו מעל  ויהי
ויהי 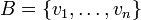 בסיס לו. יהיו
בסיס לו. יהיו 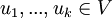 וקטורים כלשהם וסקלארים
וקטורים כלשהם וסקלארים 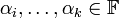 . הוכח:
. הוכח:
![\sum_{i=1}^k\alpha_i[u_i]_B =[\sum_{i=1}^k\alpha_iu_i]_B](/images/math/6/6/e/66e1b9d92df29643fbd74cc04f8f7bd6.png)
הוכחה:
מ"ל את הטענה ![[u_1]_B+[u_2]_B =[u_1+u_2]_B](/images/math/f/e/6/fe6f4a8a7637affe850bf88876db5400.png) ואת הטענה
ואת הטענה ![\alpha[u_1]_B=[\alpha u_1]_B](/images/math/4/1/0/4101ecde6459d60d491b0789f18faaea.png) (ואז המעבר לצ"ל כללי נעשה ע"י אינדוקציה)
(ואז המעבר לצ"ל כללי נעשה ע"י אינדוקציה)
נסמן 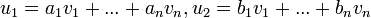 אזי
אזי 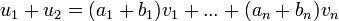 ומתקיים
ומתקיים
![[u_1]_B+[u_2]_B =\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix} + \begin{pmatrix}b_1 \\ b_2 \\ \vdots \\ b_n\end{pmatrix} =
\begin{pmatrix}a_1+b_1 \\ a_2+b_2 \\ \vdots \\ a_n+b_n\end{pmatrix}
[u_1+u_2]_B](/images/math/5/7/0/570cefc8bdea30b1d706c0b75b2f1497.png)
בנוסף 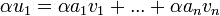 ומתקיים
ומתקיים
![\alpha[u_1]_B= \alpha \begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}=
\begin{pmatrix} \alpha_1 \\ \alpha a_2 \\ \vdots \\\alpha a_n\end{pmatrix} =
[\alpha u_1]_B](/images/math/4/f/1/4f198fa88b97fb3e7120f3aa9d75614f.png)
מש"ל
מסקנה:
2. 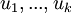 בת"ל אם"ם
בת"ל אם"ם ![[u_1]_B,...,[u_k]_B](/images/math/e/b/4/eb4b5b4e735834a276365d7282070e08.png) בת"ל
בת"ל
3. 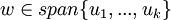 אם"ם
אם"ם ![[w]_B\in span\{[u_1]_B,...,[u_k]_B\}](/images/math/4/3/f/43f3b16647cd917a0ad42cf8adb05eb9.png)
הוכחה:
2. 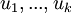 בת"ל
בת"ל
אמ"מ
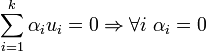
אמ"מ
![[\sum_{i=1}^k\alpha_iu_i]_B=[0]_B=0 \Rightarrow \forall i \; \alpha_i =0](/images/math/3/5/b/35beccff1789045cbe258cdf479ca3e8.png)
אמ"מ
![\sum_{i=1}^k\alpha_i[u_i]_B=0 \Rightarrow \forall i \; \alpha_i =0](/images/math/b/5/7/b57b607eb9d09cf4e0791a38218135b3.png)
אמ"מ
![[u_1]_B,...,[u_k]_B](/images/math/e/b/4/eb4b5b4e735834a276365d7282070e08.png) בת"ל
בת"ל
3. ברעיון דומה
מה בעצם המסקנה אומרת? שכל בדיקה/חישוב של תלות לינארית או פרישה בכל מרחב וקטורי (מטריצות, פולינומים, פונקציות) יכול בעצם להעשות במרחב הוקטורי המוכר והנוח 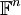 .
.
ועוד הגדרה לפני ההמשך, עד כה דיברנו "רק" על ייצוג של וקטורים לפי בסיס. אפשר להכליל בפשטות לכל המרחב הוקטורי. הנה ההגדרה:
הגדרה :
יהא  מ"ו (או תת מרחב) ויהי
מ"ו (או תת מרחב) ויהי  בסיס לו. אזי מרחב הקורדיאנטות (של
בסיס לו. אזי מרחב הקורדיאנטות (של  לפי בסיס
לפי בסיס  ) הוא
) הוא
![[V]_B = \{[v]_B \; | \; v\in V\}](/images/math/3/1/3/313fb9e5feba07386dc6ed9cb2687482.png)
הערה : יהא  מ"ו,
מ"ו, 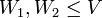 תתי מרחבים ו
תתי מרחבים ו  בסיס. אזי
בסיס. אזי
דוגמאות ואלגוריתמים
חיתוך תת מרחבים
תרגיל 7.31
נגדיר שני תתי מרחבים של ![\mathbb{R}_3[x]](/images/math/8/4/e/84ef8e18caf28275bb31fb78edc3a348.png) :
:
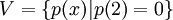 , ו
, ו 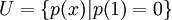
מצא את המימד של חיתוך המרחבים.
פתרון.
בתרגיל זה נשתמש בשיטה נפוצה ביותר. אנו מעוניינים לתאר את המרחבים הוקטוריים באופן קל יותר לעבודה מאשר התיאור לעיל; לכן ננסה לתאר את תתי המרחבים הללו כמרחבי פתרון של מערכת הומוגנית (אחת מהדרכים להצגת תת מרחב מתירגול קודם). המשתנים שלנו במערכת המשוואות יהיו המקדמים של הפולינומים.
נביט ב  . זהו אוסף כל הפולינומים ש2 הוא שורש שלהם. יהי פולינום כללי
. זהו אוסף כל הפולינומים ש2 הוא שורש שלהם. יהי פולינום כללי 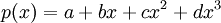 , הוא שייך ל
, הוא שייך ל אם"ם מקדמיו מקיימים את המשוואה הלינארית:
אם"ם מקדמיו מקיימים את המשוואה הלינארית: 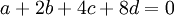 . לכן
. לכן 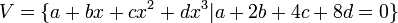 אם נעבוד עם הבסיס הסטנדרטי
אם נעבוד עם הבסיס הסטנדרטי  נקבל כי
נקבל כי
![[V]_S=\{\begin{pmatrix}a\\ b\\ c\\ d \end{pmatrix}\in \mathbb{R}^4 |a+2b+4c+8d=0\}](/images/math/f/1/7/f176c31f1ea28759ce3f8e7191041912.png)
באופן דומה הפולינום שייך ל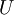 אם"ם מקדמיו מקיימים את המשוואה הלינארית
אם"ם מקדמיו מקיימים את המשוואה הלינארית 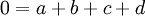 . ומרחב הקורדינאטות הוא
. ומרחב הקורדינאטות הוא
![[U]_S=\{\begin{pmatrix}a\\ b\\ c\\ d \end{pmatrix}\in \mathbb{R}^4 |a+b+c+d=0\}](/images/math/1/a/c/1acabaa6d76367bb789b9f9ff12acbb6.png)
את החיתוך ![[V]_S\cap[U]_S](/images/math/f/8/8/f88d12ef65db0dd3e46c43fad5562239.png) קל למצוא! ראינו איך עושים זאת זה פשוט שווה ל
קל למצוא! ראינו איך עושים זאת זה פשוט שווה ל
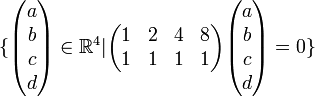
נדרג את המטריצה ונמצא את הפתרון:
עיבוד הנוסחה נכשל (שגיאת תחביר): \begin{pmatrix} 1 & 2 & 4 & 8 \\ 1 & 1 & 1 & 1 \end{pmatrix} \to \begin{pmatrix} 1 & 2 & 4 & 8 \\ 0 & -1 & -3 & -7 \end{pmatrix} \to \\ \begin{pmatrix} 1 & 0 & -2 & -6 \\ 0 & -1 & -3 & -7 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & -2 & -6 \\ 0 & 1 & 3 & 7 \end{pmatrix}
ולכן הפתרון הכללי הוא מהצורה 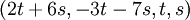 , ולכן הבסיס הינו
, ולכן הבסיס הינו 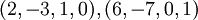 .
.
נחזור לצורה הפולינומית לקבל את התשובה הסופית:
![U\cap V = sapn \{v_1, v_2 \; | \; [v_1]_s = (2,-3,1,0), [v_2]_s = (6,-7,0,1) \} = span\{2-3x+x^2,6-7x+x^3\}](/images/math/a/a/6/aa61e8dcad1d7dc71a94bd20126c8103.png)
אלגוריתם למציאת חיתוך בין שני תתי מרחבים U,W
ישנן שתי שיטות לחשב את החיתוך, נתחיל בראשונה (שביצענו הרגע, למעשה):
- החלף את
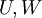 במרחב הקורדינאטות שלהם.
במרחב הקורדינאטות שלהם. - מצא מערכת משוואות המתארת את
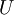 ומערכת משוואות המתארת את
ומערכת משוואות המתארת את 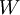
- פתור מערכת אחת המכילה את כל המשוואות משתי המערכות וקבל את החיתוך
- חזור ל
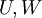 המקוריים.
המקוריים.
שיטה שנייה:
- החלף את
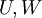 במרחב הקורדינאטות שלהם.
במרחב הקורדינאטות שלהם. - הצג את המרחבים כ
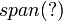
- כתוב צירוף לינארי כללי ב
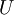 וצירוף לינארי כללי ב
וצירוף לינארי כללי ב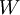
- השווה את הצירופים ופתור מערכת משוואות על הסקלרים
- הצב את הסקלרים שקיבלת בצירוף הלינארי וקבל את החיתוך
- חזור ל
 המקוריים.
המקוריים.
תרגיל =
מצא את החיתוך בין תתי המרחבים הבאים בשיטה השנייה לעיל.
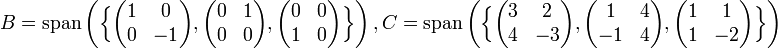
פתרון.
(קחו נשימה עמוקה) יהיו סקלרים a,b,c,x,y,z, וקטור הוא בחיתוך אם"ם הוא צירוף לינארי של שתי הקבוצות הפורשות:
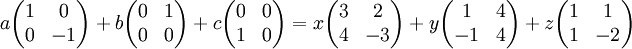
במרחב הקורדינאטות (עם הבסיס הסטדנדרטי  , נקבל את השיוון
, נקבל את השיוון
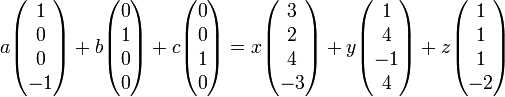
לכן מערכת המשוואות על הסקלרים הינה:
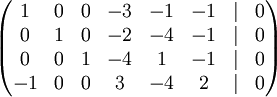
נדרג ונמצא את הפתרונות (שימו לב: מספיק למצוא רק את x,y,z או רק את a,b,c מכיוון שבהנתן צירוף לינארי של איברי C שנותן את החיתוך אין צורך להמשיך (כמו כן לגבי B).)
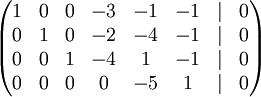
במקרה זה קל יותר למצוא את x,y,z; המשתנים החופשיים הינם x,z ומתקיים z=5y. ולכן הצ"ל הכללי בחיתוך הינו:
עיבוד הנוסחה נכשל (שגיאת תחביר): [B]_S \cap [C]_S= \Big\{x\begin{pmatrix} 3 \\ 2 \\ 4 \\ -3\end{pmatrix}+y\begin{pmatrix}1 \\ 4 \\ -1 \\ 4 \end{pmatrix}+5y\begin{pmatrix}1 \\ 1 \\ 1 \\ -2\end{pmatrix}\Big\}= \\ \Big\{x\begin{pmatrix} 3 \\ 2 \\ 4 \\ -3\end{pmatrix}+y\begin{pmatrix}6 \\ 9 \\ 4 \\ -6 \end{pmatrix}\Big\}= span\Big\{\begin{pmatrix} 3 \\ 2 \\ 4 \\-3\end{pmatrix},\begin{pmatrix}6 \\ 9 \\ 4 \\ -6 \end{pmatrix}\Big\}
אם נחזור למרחבים המקוריים נקבל כי
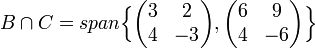
תלות לינארית
דוגמא.
האם הפולינומים 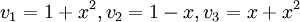 תלויים לינארית?
תלויים לינארית?
דבר ראשון, נעבור למרחב הקואורדינטות. מכיוון שבחירת הבסיס היא לשיקולנו, נבחר את הבסיס הסטנדרטי S של הפולינומים איתו קל לעבוד. מתקיים ש ![[v_1]_S=(1,0,1),[v_2]_S=(1,-1,0),[v_3]_S=(0,1,1)](/images/math/7/c/e/7ce5727bd083202ed16a83d37b21d213.png)
הוכחנו בשיעור שעבר שוקטורים "רגילים" ת"ל אם"ם המטריצה שהם השורות שלה אינה הפיכה אם"ם הצורה המדורגת של המטריצה מכילה שורת אפסים. לכן, נשים את וקטורי הקואורדינטות בשורות מטריצה ונדרג.
![\begin{pmatrix}1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 1 & 1\end{pmatrix}
\xrightarrow[]{R_3-R_1,R_3+R_2}
\begin{pmatrix}1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 0 & 0\end{pmatrix}](/images/math/4/8/3/4836a322a3655d593342cc0784f734a0.png)
לכן וקטורי הקואורדינטות תלויים לינארית ולכן הפולינומים עצמם תלויים לינארית.
דרך נוספת: נשים את הוקטורים בעמודה של מטריצה  . צ"ל של עמודות
. צ"ל של עמודות  זה פשוט
זה פשוט 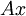 . ולכן הוקטורים בת"ל אמ"מ הפתרון היחידי למערכת
. ולכן הוקטורים בת"ל אמ"מ הפתרון היחידי למערכת 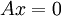 (צ"ל שמתאפס) הוא הפתרון הטריאלי (הצ"ל הטריאלי)
(צ"ל שמתאפס) הוא הפתרון הטריאלי (הצ"ל הטריאלי)
עיבוד הנוסחה נכשל (שגיאת לקסינג): \begin{pmatrix}1 & 1 & 0 \\ 0 & -1 & 1 \\ 1 & 0 & 1\end{pmatrix} \to \begin{pmatrix}1 & 1 & 0 \\ 0 & -1 & 1 \\ 0 & -1 & 1\end{pmatrix} \to \begin{pmatrix}1 & 1 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & 0\end{pmatrix} \
קיבלנו שיש משתנים חופשיים ולכן יש פתרון לא טרויאלי ולכן הוקטורים תלויים לינארית!
נסכם את התהליך:
אלגוריתם לבדיקת תלות לינארית בין וקטורים
- הפוך את הוקטורים לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים
- שים את וקטורי הקואורדינטות בשורות מטריצה A
- הבא את המטריצה לצורה מדורגת
- אם באיזה שלב קיבלת שורת אפסים סימן שהוקטורים תלויים לינארית
- אם הגעת לצורה מדורגת ללא שורת אפסים סימן שהוקטורים בלתי תלויים לינארית
ובדרך הנוספת
- הפוך את הוקטורים לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים
- שים את וקטורי הקואורדינטות בעמודות מטריצה A
- בדוק אם יש פתרון לא טריאלי למערכת
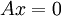
- אם יש אז הם תלויים ואם אין אז הם בת"ל
צירופים לינאריים
דוגמא.
האם המטריצה 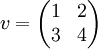 היא צ"ל של המטריצות
היא צ"ל של המטריצות
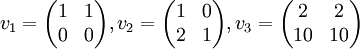 ?
אם כן, הצג אותה כצירוף לינארי שלהן.
?
אם כן, הצג אותה כצירוף לינארי שלהן.
פתרון: נעבור דבר ראשון למרחב הקואורדינטות לפי הבסיס הסטנדרטי 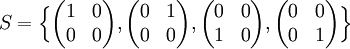
נקבל ![[v]_S=(1,2,3,4),[v_1]_S=(1,1,0,0),[v_2]_S=(1,0,2,1),[v_3]_S=(2,2,10,10)](/images/math/c/e/b/cebc685addea9d107edc1c2d44ec2667.png) .
.
למדנו בשיעור שעבר שוקטור b נפרש על ידי וקטורים מסויימים אם"ם קיים פתרון למערכת Ax=b כאשר A היא המטריצה שעמודותיה הם אותם וקטורים. הפתרון x הוא וקטור הסקלרים מהצירוף הלינארי. לכן, אנו רוצים לדעת האם קיים פתרון למערכת ואם כן מהו:
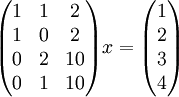
קל לפתור ולגלות ש 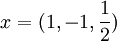 מקיים את המערכת ולכן מתקיים
מקיים את המערכת ולכן מתקיים 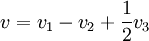
נסכם:
אלגוריתם לחישוב צירוף לינארי
- נתון וקטור b וקבוצת וקטורים. העבר את כולם לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים
- פתור את המערכת Ax=b כאשר עמודות A הינן וקטורי הקואורדינטות של קבוצת הוקטורים הפורשים
- אם אין פתרון, b לא נפרש על ידי האחרים
- אם קיים פתרון x אזי הוא מכיל את הסקלרים של הצירוף הלינארי בהתאם לסדר העמודות בA
מטריצות מעבר בין בסיסים
ראינו שקל מאד למצוא קואורדינטות לפי הבסיס הסטנדרטי, נשתמש בהנחה הזו בהמשך. אנו מעוניינים לדעת כיצד לחשב קואורדינטות לפי בסיס כלשהו, לאו דווקא סטנדרטי.
משפט: יהא  מ"ו ויהיו
מ"ו ויהיו 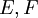 בסיסים לו. אזי קיימת מטריצה יחידה המסומנת
בסיסים לו. אזי קיימת מטריצה יחידה המסומנת ![[I]^E_F](/images/math/2/b/d/2bdc7db12150a97716a9a1c21d1742c9.png) המקיימת את הפסוק הבא:
המקיימת את הפסוק הבא:
![\forall v\in V: [I]^E_F[v]_E=[v]_F](/images/math/1/7/b/17b12c597f8e46ebafb02da9deabffb8.png)
נסמן 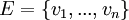 ו
ו 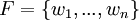 . אזי מתקיים ש
. אזי מתקיים ש![[I]^E_F](/images/math/2/b/d/2bdc7db12150a97716a9a1c21d1742c9.png) הינה המטריצה שעמודותיה הן
הינה המטריצה שעמודותיה הן ![[v_i]_F](/images/math/c/d/b/cdb0e6ced2f77815790fb78f605b8d84.png)
דוגמא.
יהא 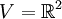 ושני בסיסים
ושני בסיסים
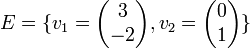 ו
ו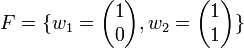
נמצא את ![[I]^E_F](/images/math/2/b/d/2bdc7db12150a97716a9a1c21d1742c9.png) .
.
מתקיים כי עיבוד הנוסחה נכשל (שגיאת תחביר): v_1 = \mathbf{5}w_1-\mathbf{2}w_2 \\ v_2 = -\mathbf{1}w_1+\mathbf{1}w_2
לכן
![[I]^E_F=
\begin{pmatrix} 5& -1 \\ -2 & 1 \end{pmatrix}](/images/math/3/7/5/37590c1232a83c92005bfba99efc4c1c.png)
תרגיל:
הוכח ש ![[I]^S_B[I]^A_S=[I]^A_B](/images/math/6/5/3/653023384226547eafe4c3661a5e7113.png) . מכיוון שאנו יודעים שמטריצה המעבר הינה יחידה, מספיק להראות שהכפל מקיים את הפסוק מההגדרה:
. מכיוון שאנו יודעים שמטריצה המעבר הינה יחידה, מספיק להראות שהכפל מקיים את הפסוק מההגדרה:
![\forall v\in V: [I]^S_B[I]^A_S[v]_A=[I]^S_B[v]_S=[v]_B](/images/math/c/b/0/cb04c4351cb813abbb3f23bda4db1c4f.png)
משפט: לכל שני בסיסים E,F מטריצת המעבר הינה מטריצה הפיכה ומתקיים ![([I]^E_F)^{-1}=[I]^F_E](/images/math/b/3/f/b3f6080673f1a30c55100cc8718d3bcb.png)
מסקנה:
אלגוריתם למציאת מטריצת מעבר בין כל שני בסיסים E,F
- בחר בסיס סטנדרטי S מתאים למרחב שלך
- מצא את מטריצת המעבר
![[I]^E_S](/images/math/b/2/b/b2b4df7772480d67ed9e272792aad633.png) . זה קל מאד שכן יש למצוא את הקואורדינטות של איברי הבסיס E לפי הבסיס הסטנדרטי S
. זה קל מאד שכן יש למצוא את הקואורדינטות של איברי הבסיס E לפי הבסיס הסטנדרטי S - מצא את מטריצת המעבר
![[I]^F_S](/images/math/9/c/8/9c891851116631d866f8316d8559a34b.png) .
. - הפוך את המטריצה האחרונה לקבל
![([I]^F_S)^{-1}=[I]^S_F](/images/math/7/6/c/76cf328ff5b7b824008b828bf38d1f43.png)
- כפול את המטריצות על מנת לקבל את התוצאה הסופית
![[I]^S_F[I]^E_S=[I]^E_F](/images/math/a/a/7/aa79b74333d9c06ccafc41034ade00a7.png)
דוגמא:
![V=\mathbb{R}_2[x]](/images/math/4/9/5/495528b4842c3efec23cbf769dd776da.png) מצא את
מצא את ![[I]^E_F](/images/math/2/b/d/2bdc7db12150a97716a9a1c21d1742c9.png) כאשר
כאשר
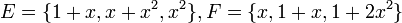
פתרון:
נסמן  הבסיס הסטנדרטי ואז
הבסיס הסטנדרטי ואז
![[I]^E_S=
\begin{pmatrix}
1 & 0 & 0 \\
1 & 1 & 0 \\
0 & 1 & 1
\end{pmatrix},
[I]^F_S=
\begin{pmatrix}
0 & 1 & 1 \\
1 & 1 & 0 \\
0 & 0 & 2
\end{pmatrix}](/images/math/7/d/4/7d432f9904181e99db2cdf7f82124c6e.png)
אחרי חישובים מקבלים כי
![[I]^S_F=
\begin{pmatrix}
0 & 1 & 1 \\
1 & 1 & 0 \\
0 & 0 & 2
\end{pmatrix}^{-1} =
\begin{pmatrix}
-1 & 1 & 0.5 \\
1 & 0 & -0.5 \\
0 & 0 & 0.5
\end{pmatrix}](/images/math/3/2/b/32bb73e9e6bbed38b50a3f5a4e0b5da5.png)
ולכן
![[I]^E_F=[I]^S_F[I]^E_S=
\begin{pmatrix}
-1 & 1 & 0.5 \\
1 & 0 & -0.5 \\
0 & 0 & 0.5
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 \\
1 & 1 & 0 \\
0 & 1 & 1
\end{pmatrix}
=
\begin{pmatrix}
0 & 1.5 & 0.5 \\
1 & -0.5 & -0.5 \\
0 & 0.5 & 0.5
\end{pmatrix}](/images/math/5/d/3/5d396bc8a6d16eeddca2f3b551ab9bc5.png)
תרגיל
תהא
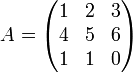
ובסיס
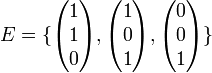
מצאו בסיס 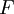 כך ש
כך ש ![A=[I]^E_F](/images/math/1/6/2/16249ef921e10bb363bf101a16d30b07.png)
פתרון:
נסמן 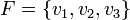
נחשב ונמצא כי
![[I]^F_E= A^{-1} =
\begin{pmatrix}
-4/3 & 1/3 & 1 \\
2/3 & 1/3 & -2 \\
1/3 & -1/3 & 1 \\
\end{pmatrix}](/images/math/1/d/d/1dd3911117c44aaf913f5c7953827e14.png)
מהגדרה נקבל כי
עיבוד הנוסחה נכשל (שגיאת תחביר): v_1 = -4/3 \begin{pmatrix} 1 \\ 1 \\ 0 \\ \end{pmatrix}+ 2/3 \begin{pmatrix} 1 \\ 0 \\ 1 \\ \end{pmatrix}+ 1/3 \begin{pmatrix} 0 \\ 0 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} -2/3 \\ -4/3 \\ 1 \\ \end{pmatrix}, \\ v_2 = 1/3 \begin{pmatrix} 1 \\ 1 \\ 0 \\ \end{pmatrix}+ 1/3 \begin{pmatrix} 1 \\ 0 \\ 1 \\ \end{pmatrix}+ -1/3 \begin{pmatrix} 0 \\ 0 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} 2/3 \\ 1/3 \\ 0 \\ \end{pmatrix}, \\ v_3 = 1 \begin{pmatrix} 1 \\ 1 \\ 0 \\ \end{pmatrix}+ -2 \begin{pmatrix} 1 \\ 0 \\ 1 \\ \end{pmatrix}+ 1 \begin{pmatrix} 0 \\ 0 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} -1 \\ 1 \\ -1 \\ \end{pmatrix}
![[W_1 \cap W_2]_B = [W_1]_B \cap [W_2]_B](/images/math/9/8/0/9803162d337b7ce9687f0ebe012304ee.png)
![[W_1 + W_2]_B = [W_1]_B + [W_2]_B](/images/math/e/5/a/e5a8acb85545509abd102f4f722cfb05.png)