הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 9"
(←טבלת סיכום לנוסחאות בסיסיות ידועות) |
|||
| (14 גרסאות ביניים של 3 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | '''[[מתמטיקה בדידה - מערך תרגול|חזרה למערכי התרגול]]''' | ||
| + | |||
| + | |||
| + | |||
=מבוא לקומבינטוריקה= | =מבוא לקומבינטוריקה= | ||
| + | |||
| + | [[מדיה:11BdidaCombBG.pdf|קובץ דוגמאות והסברים בקומבינטוריקה מבן גוריון]] | ||
קומבינטוריקה הוא ענף במתמטיקה העוסק בספירת עצמים המקיימים תכונה מסוימת. לדוגמא, כמה תוצאות אפשריות שונות יש למשחקי הכדורגל (על מנת למלא טופס וינר). | קומבינטוריקה הוא ענף במתמטיקה העוסק בספירת עצמים המקיימים תכונה מסוימת. לדוגמא, כמה תוצאות אפשריות שונות יש למשחקי הכדורגל (על מנת למלא טופס וינר). | ||
| שורה 9: | שורה 15: | ||
'''פתרון.''' למעשה בעייה זו שקולה לבעיית חלוקת 10 אנשים לשתי קבוצות שונות בלבד, מכיוון שיש רק דרך אחת למיין את האנשים לפי הסדר של התור המקורי בכל תת קבוצה. נלמד בהמשך כיצד לפתור בעייה פשוטה זו. | '''פתרון.''' למעשה בעייה זו שקולה לבעיית חלוקת 10 אנשים לשתי קבוצות שונות בלבד, מכיוון שיש רק דרך אחת למיין את האנשים לפי הסדר של התור המקורי בכל תת קבוצה. נלמד בהמשך כיצד לפתור בעייה פשוטה זו. | ||
| + | ==מספר האפשרויות לסדר n עצמים שונים בשורה == | ||
'''דוגמא.''' בכמה דרכים אפשר לסדר n אנשים בתור? | '''דוגמא.''' בכמה דרכים אפשר לסדר n אנשים בתור? | ||
| שורה 14: | שורה 21: | ||
'''פתרון.''' כל אחד יכול להיות ראשון בתור לכן כבר יש n אפשרויות. כעת, נניח ואיציק ראשון בתור, נותר לסדר n-1 אנשים אחריו בתור. נניח באינדוקציה שמספר האפשרויות לסדר n-1 אנשים בתור הוא <math>(n-1)!</math> ונקבל שמספר האפשרויות שלנו הוא <math>n\cdot (n-1)! = n!</math>. | '''פתרון.''' כל אחד יכול להיות ראשון בתור לכן כבר יש n אפשרויות. כעת, נניח ואיציק ראשון בתור, נותר לסדר n-1 אנשים אחריו בתור. נניח באינדוקציה שמספר האפשרויות לסדר n-1 אנשים בתור הוא <math>(n-1)!</math> ונקבל שמספר האפשרויות שלנו הוא <math>n\cdot (n-1)! = n!</math>. | ||
| + | |||
| + | == מספר האפשריות לבחור k עצמים מתוך n עצמים== | ||
| + | השאלות שצריך לשאול הם- האם יש חשיבות לסדר (הבחירה) והאם מותר לבחור איבר פעמיים. לכן ישנם 4 מקרים אפשריים. | ||
| + | |||
| + | נשים לב שאם אסור חזרות אזי חייב להיות <math>k\leq n</math> (אחרת התשובה היא 0) | ||
| + | |||
| + | {| border="1" align="center" style="text-align:center;" | ||
| + | | | ||
| + | |'''אין חזרות''' | ||
| + | |'''יש חזרות''' | ||
| + | |- | ||
| + | |''' יש חשיבות לסדר''' | ||
| + | |<math>\frac{n!}{(n-k)!}</math> | ||
| + | | <math>n^k</math> | ||
| + | |- | ||
| + | |'''אין חשיבות לסדר''' | ||
| + | |<math>\;\;\;{n \choose k} = \frac{n!}{k!(n-k)!} \;\;\;</math> | ||
| + | |<math>\;\;\;{n+k-1\choose k}\;\;\;</math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | נתחיל לטפל בכל אחד מהמקרים: | ||
| + | |||
| + | === יש חשיבות לסדר ויש חזרות === | ||
| + | בהנתן n עצמים אזי בבחירה הראשונה ניתן יש n אפשרויות לבחור ולבחירה השניה יש n אפשריות לבחור (כי מותר חזרות), ... ,לבחירה ה-k יש n אפשרויות לבחור ולכן בסה"כ יש <math>n^k</math> אפשרויות. | ||
| + | |||
| + | '''דוגמא''' כמה מספרים בינאריים יש עם 3 ספרות ? | ||
| + | |||
| + | ''' פתרון''' לספרה הראשונה יש 2 אפשרויות, לספרה השניה יש 2 אפשרויות ולספרה השלישית יש 2 אפשריות ולכן בסה"כ יש <math>2^3</math> וזה כל המספרים. (הבחירה היא הספרות 0,1 כאשר מותר חזרות ויש חשיבות לסדר) | ||
| + | |||
| + | === יש חשיבות לסדר ואין חזרות === | ||
| + | נסדר את n החפצים בשורה וניקח את k הראשונים. ככה אנחנו מבטיחים שאין חזרות ויש חשיבות לסדר. דא עקא, בשיטה זו אנחנו מקבלים כפילויות. | ||
| + | כמה כפילויות יש לנו? במילים אחרות כמה פעמים נקבל את אותה סדרת k חפצים? בדיוק כמספר הפעמים שאפשר לסדר את n-k החפצים הנותרים. כיוון שאותם ניתן לסדר ב <math>(n-k)!</math> אפשרויות | ||
| + | נקבל שמספר האפשריות לבחירת k עצמים מתוך n עם חשיבות לסדר ובלי חזרות הוא <math>\frac{n!}{(n-k)!}</math> | ||
| + | |||
| + | '''דוגמא''' כמה מספרים בעלי 3 ספרות שונות יש? | ||
| + | |||
| + | ''' פתרון''' נבחר מתוך הספרות 0-9 שלוש בחירות עם חשיבות לסדר ובלי חזרות ונקבל <math>\frac{10!}{(7)!}=10\cdot 9 \cdot 8</math> (לספרה הראשונה יש 10 אפשרויות, לספרה השניה יש רק 9 אפשרויות ולספרה האחרונה נשארו 8 אפשרויות) | ||
| + | |||
| + | |||
| + | === אין חשיבות לסדר ואין חזרות === | ||
| + | נבחר k עצמים עם חשיבות לסדר ובלי חזרות. כעת אם רוצים שלא יהיה חשיבות לסדר צריך לחלק בכל ה- <math>k!</math> אפשריות לסידור k איברים ולכן מספר האפשרויות לבחור k עצמים בלי חשיבות לסדר ובלי חזרות | ||
| + | הינו <math>\;\;\;{n \choose k} = \frac{n!}{k!(n-k)!} \;\;\;</math> | ||
'''דוגמא.''' בכמה דרכים ניתן לבחור קבוצה של k חפצים מתוך קבוצה של n חפצים? (במילים אחרות, כמה תת קבוצות מעוצמת k יש לקבוצה מגודל n). | '''דוגמא.''' בכמה דרכים ניתן לבחור קבוצה של k חפצים מתוך קבוצה של n חפצים? (במילים אחרות, כמה תת קבוצות מעוצמת k יש לקבוצה מגודל n). | ||
| + | '''פתרון.''' זה שקול לבחור k חפצים כאשר הסדר לא משנה ובלי חזרות ולכן יש <math> {n \choose k} </math> תתי קבוצות. | ||
| − | + | מסקנה: <math>\sum_{k=0}^n {n \choose k}=2^n</math> | |
| − | + | הוכחה: ניקח קבוצה X בת n איברים אזי שני האגפים שווים למספר הקבוצות של בקבוצת החזקה. | |
| − | + | '''תרגיל''' הוכח כי <math> {n \choose k}= {n \choose n-k}</math> | |
| + | '''פתרון''' לבחור קבוצה של k אברים שקול לבחור n-k אברים שאינם בקבוצה (כלומר לבחור תת קבוצה A זה כמו לבחור את המשלימה שלה) | ||
| + | אתם מוזמנים גם לחשב ישירות. | ||
| + | |||
| + | |||
| + | === אין חשיבות לסדר ויש חזרות === | ||
'''תרגיל.''' כמה פתרונות שלמים אי שליליים יש למשוואה <math>x_1+...+x_n=k</math>? | '''תרגיל.''' כמה פתרונות שלמים אי שליליים יש למשוואה <math>x_1+...+x_n=k</math>? | ||
| − | '''פתרון.''' נחלק את המספר k לאחדות, | + | '''פתרון.''' נחלק את המספר <math>k=1+1+1\cdots+1</math> לאחדות, ונחלק את האחדות ל-n המשתנים האפשריים. |
| + | נעשה זאת כך- נשים n-1 חוצצים בין n המשתנים ונחלק 1-ים לפי כמות ה-1-ים שכל משתנה מקבל. | ||
למשל נביט בפתרונות שונים למשוואה <math>x_1+x_2+x_3=2</math>: | למשל נביט בפתרונות שונים למשוואה <math>x_1+x_2+x_3=2</math>: | ||
| שורה 39: | שורה 96: | ||
| − | + | כעת, יש לנו <math>n+k-1</math> מקומות שצריך למלא (k אחדות ו n-1 חוצצים) וצריך לבחור מתוכם את המקומות של החוצצים (ואז ממילא יקבעו מקומות של האחדות) ולכן יש | |
| + | <math>{n+k-1\choose k}=\frac{(n+k-1)!}{k!(n-1)!}</math> אפשריות כאלו. | ||
| + | '''מסקנה''' מספר הדרכים שיש לבחור k איברים מתוך קבוצה של n איברים כאשר מותר לי לבצע חזרות ולא משנה הסדר הוא <math>{n+k-1\choose k}</math> | ||
| − | ''' | + | '''הוכחה''' |
| − | + | נסמן את האיברים בקבוצה <math>a_1,...,a_n</math>. נסמן את מספר החזרות של כל איבר <math>a_i</math> ב-<math>x_i</math> (שלם אי שלילי). | |
| + | כיוון שרוצים לבחור k איברים השאלה שקולה ל-כמה פתרונות שלמים אי שליליים יש למשוואה <math>x_1+...+x_n=k</math> שראינו שהתשובה היא <math>{n+k-1\choose k}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| שורה 75: | שורה 130: | ||
א. ניתן לבחור כל מספר מ1 עד 100. כעת, המספר המתאים לו צריך להיות מאותה זוגיות על מנת שהסכום יהיה זוגי. לכן בבחירה הראשונה היו לנו 100 אפשרויות ובשנייה 49. כעת, סדר הזוג לא משנה לכן נחלק ב2. סה"כ התוצאה היא <math>50\cdot 49</math>. זה בדיוק שווה לסעיף 1, שכן | א. ניתן לבחור כל מספר מ1 עד 100. כעת, המספר המתאים לו צריך להיות מאותה זוגיות על מנת שהסכום יהיה זוגי. לכן בבחירה הראשונה היו לנו 100 אפשרויות ובשנייה 49. כעת, סדר הזוג לא משנה לכן נחלק ב2. סה"כ התוצאה היא <math>50\cdot 49</math>. זה בדיוק שווה לסעיף 1, שכן | ||
| − | <math>{50 \choose 2}+{50 \choose 2} | + | <math>{50 \choose 2}+{50 \choose 2}=2{50 \choose 2} = 2\frac{50!}{2!48!}=2\frac{50\cdot 49}{2}</math> |
| שורה 83: | שורה 138: | ||
ב. ניתן לבחור שלושה מספרים זוגיים, או שני אי זוגיים וזוגי. <math>{50 \choose 3}+{50\choose 2}\cdot{50 \choose 1}</math> | ב. ניתן לבחור שלושה מספרים זוגיים, או שני אי זוגיים וזוגי. <math>{50 \choose 3}+{50\choose 2}\cdot{50 \choose 1}</math> | ||
| − | ג. נסמן <math>|A|=a</math>. מספרים היחסים על A הוא קבוצת החזקה של <math>A\times A</math> שזה <math>2^{|A\times A|}=2^{a^2}</math>. כעת, פונקציה חד ערכית מקבוצה בגודל k אל קבוצה בגודל n מכילה <math>n\cdot (n-1) \cdots (n-k+1)=\frac{n!}{k!}</math> איברים. | + | ג. נסמן <math>|A|=a</math>. מספרים היחסים על A הוא קבוצת החזקה של <math>A\times A</math> שזה <math>2^{|A\times A|}=2^{a^2}</math>. כעת, פונקציה חד ערכית מקבוצה בגודל k אל קבוצה בגודל n מכילה |
| + | <math>n\cdot (n-1) \cdots (n-k+1)=\frac{n!}{(n-k)!}</math> איברים. | ||
אבל, חייב להתקיים ש k<n אחרת לא תתכן פונקציה חח"ע (והנוסחא כמובן לא תהא הגיונית), במקרה שלנו <math>2^{a^2}>a</math> ולכן אין אף פונקציה חח"ע מקבוצת היחסים של A אל A. | אבל, חייב להתקיים ש k<n אחרת לא תתכן פונקציה חח"ע (והנוסחא כמובן לא תהא הגיונית), במקרה שלנו <math>2^{a^2}>a</math> ולכן אין אף פונקציה חח"ע מקבוצת היחסים של A אל A. | ||
| שורה 96: | שורה 152: | ||
|<math>n!</math> | |<math>n!</math> | ||
|- | |- | ||
| − | |מספר האפשרויות לבחור קבוצה של k תלמידים מתוך כיתה של n תלמידים | + | |מספר האפשרויות לבחור קבוצה של k תלמידים מתוך כיתה של n תלמידים '''(ללא משמעות לסדר, ללא חזרות)''' |
|<math>{n \choose k} = \frac{n!}{k!(n-k)!}</math> | |<math>{n \choose k} = \frac{n!}{k!(n-k)!}</math> | ||
|- | |- | ||
| − | |מספר האפשרויות לבנות סדרה עם k איברים מתוך קבוצה המכילה מ איברים | + | |מספר האפשרויות לבנות סדרה עם k איברים מתוך קבוצה המכילה מ איברים '''(עם משמעות לסדר, ועם חזרות)''' |
|<math>n^k</math> | |<math>n^k</math> | ||
|- | |- | ||
| − | |מספר האפשרויות לבנות סדרה עם k איברים '''שונים''' מתוך קבוצה המכילה n איברים | + | |מספר האפשרויות לבנות סדרה עם k איברים '''שונים''' מתוך קבוצה המכילה n איברים '''(עם משמעות לסדר, ללא חזרות)''' |
|<math>\frac{n!}{(n-k)!}</math> | |<math>\frac{n!}{(n-k)!}</math> | ||
|- | |- | ||
| − | |מספר האפשרויות לבחור k איברים מתוך n איברים | + | |מספר האפשרויות לבחור k איברים מתוך n איברים '''(ללא משמעות לסדר, עם חזרות)''' |
|<math>{n+k-1\choose k}=\frac{(n+k-1)!}{k!(n-1)!}</math> | |<math>{n+k-1\choose k}=\frac{(n+k-1)!}{k!(n-1)!}</math> | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
|} | |} | ||
גרסה אחרונה מ־16:17, 11 במרץ 2015
תוכן עניינים
מבוא לקומבינטוריקה
קובץ דוגמאות והסברים בקומבינטוריקה מבן גוריון
קומבינטוריקה הוא ענף במתמטיקה העוסק בספירת עצמים המקיימים תכונה מסוימת. לדוגמא, כמה תוצאות אפשריות שונות יש למשחקי הכדורגל (על מנת למלא טופס וינר).
אנו נלמד כיצד לחשב ישירות את מספר האפשרויות או כיצד להציג את הבעייה באופן שקול אותו אנו יודעים לחשב.
דוגמא. 10 אנשים עומדים בתור למכולת, כאשר בעל המכולת החליט להוסיף קופאי. כמה דרכים ישנן לחלק את האנשים בין הקופאים כך שלא יהיה אדם אחד בתור מאחורי אדם אחר שהיה לפניו בתור?
פתרון. למעשה בעייה זו שקולה לבעיית חלוקת 10 אנשים לשתי קבוצות שונות בלבד, מכיוון שיש רק דרך אחת למיין את האנשים לפי הסדר של התור המקורי בכל תת קבוצה. נלמד בהמשך כיצד לפתור בעייה פשוטה זו.
מספר האפשרויות לסדר n עצמים שונים בשורה
דוגמא. בכמה דרכים אפשר לסדר n אנשים בתור?
פתרון. כל אחד יכול להיות ראשון בתור לכן כבר יש n אפשרויות. כעת, נניח ואיציק ראשון בתור, נותר לסדר n-1 אנשים אחריו בתור. נניח באינדוקציה שמספר האפשרויות לסדר n-1 אנשים בתור הוא 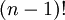 ונקבל שמספר האפשרויות שלנו הוא
ונקבל שמספר האפשרויות שלנו הוא 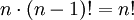 .
.
מספר האפשריות לבחור k עצמים מתוך n עצמים
השאלות שצריך לשאול הם- האם יש חשיבות לסדר (הבחירה) והאם מותר לבחור איבר פעמיים. לכן ישנם 4 מקרים אפשריים.
נשים לב שאם אסור חזרות אזי חייב להיות 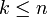 (אחרת התשובה היא 0)
(אחרת התשובה היא 0)
| אין חזרות | יש חזרות | |
| יש חשיבות לסדר | 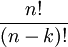
|
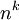
|
| אין חשיבות לסדר | 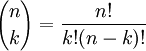
|
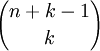
|
נתחיל לטפל בכל אחד מהמקרים:
יש חשיבות לסדר ויש חזרות
בהנתן n עצמים אזי בבחירה הראשונה ניתן יש n אפשרויות לבחור ולבחירה השניה יש n אפשריות לבחור (כי מותר חזרות), ... ,לבחירה ה-k יש n אפשרויות לבחור ולכן בסה"כ יש 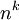 אפשרויות.
אפשרויות.
דוגמא כמה מספרים בינאריים יש עם 3 ספרות ?
פתרון לספרה הראשונה יש 2 אפשרויות, לספרה השניה יש 2 אפשרויות ולספרה השלישית יש 2 אפשריות ולכן בסה"כ יש 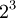 וזה כל המספרים. (הבחירה היא הספרות 0,1 כאשר מותר חזרות ויש חשיבות לסדר)
וזה כל המספרים. (הבחירה היא הספרות 0,1 כאשר מותר חזרות ויש חשיבות לסדר)
יש חשיבות לסדר ואין חזרות
נסדר את n החפצים בשורה וניקח את k הראשונים. ככה אנחנו מבטיחים שאין חזרות ויש חשיבות לסדר. דא עקא, בשיטה זו אנחנו מקבלים כפילויות.
כמה כפילויות יש לנו? במילים אחרות כמה פעמים נקבל את אותה סדרת k חפצים? בדיוק כמספר הפעמים שאפשר לסדר את n-k החפצים הנותרים. כיוון שאותם ניתן לסדר ב 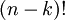 אפשרויות
נקבל שמספר האפשריות לבחירת k עצמים מתוך n עם חשיבות לסדר ובלי חזרות הוא
אפשרויות
נקבל שמספר האפשריות לבחירת k עצמים מתוך n עם חשיבות לסדר ובלי חזרות הוא 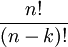
דוגמא כמה מספרים בעלי 3 ספרות שונות יש?
פתרון נבחר מתוך הספרות 0-9 שלוש בחירות עם חשיבות לסדר ובלי חזרות ונקבל 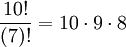 (לספרה הראשונה יש 10 אפשרויות, לספרה השניה יש רק 9 אפשרויות ולספרה האחרונה נשארו 8 אפשרויות)
(לספרה הראשונה יש 10 אפשרויות, לספרה השניה יש רק 9 אפשרויות ולספרה האחרונה נשארו 8 אפשרויות)
אין חשיבות לסדר ואין חזרות
נבחר k עצמים עם חשיבות לסדר ובלי חזרות. כעת אם רוצים שלא יהיה חשיבות לסדר צריך לחלק בכל ה- 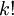 אפשריות לסידור k איברים ולכן מספר האפשרויות לבחור k עצמים בלי חשיבות לסדר ובלי חזרות
הינו
אפשריות לסידור k איברים ולכן מספר האפשרויות לבחור k עצמים בלי חשיבות לסדר ובלי חזרות
הינו 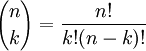
דוגמא. בכמה דרכים ניתן לבחור קבוצה של k חפצים מתוך קבוצה של n חפצים? (במילים אחרות, כמה תת קבוצות מעוצמת k יש לקבוצה מגודל n).
פתרון. זה שקול לבחור k חפצים כאשר הסדר לא משנה ובלי חזרות ולכן יש  תתי קבוצות.
תתי קבוצות.
מסקנה: 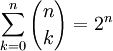
הוכחה: ניקח קבוצה X בת n איברים אזי שני האגפים שווים למספר הקבוצות של בקבוצת החזקה.
תרגיל הוכח כי 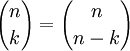
פתרון לבחור קבוצה של k אברים שקול לבחור n-k אברים שאינם בקבוצה (כלומר לבחור תת קבוצה A זה כמו לבחור את המשלימה שלה)
אתם מוזמנים גם לחשב ישירות.
אין חשיבות לסדר ויש חזרות
תרגיל. כמה פתרונות שלמים אי שליליים יש למשוואה 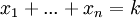 ?
?
פתרון. נחלק את המספר 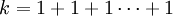 לאחדות, ונחלק את האחדות ל-n המשתנים האפשריים.
נעשה זאת כך- נשים n-1 חוצצים בין n המשתנים ונחלק 1-ים לפי כמות ה-1-ים שכל משתנה מקבל.
לאחדות, ונחלק את האחדות ל-n המשתנים האפשריים.
נעשה זאת כך- נשים n-1 חוצצים בין n המשתנים ונחלק 1-ים לפי כמות ה-1-ים שכל משתנה מקבל.
למשל נביט בפתרונות שונים למשוואה 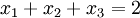 :
:
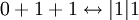
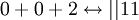
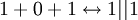
כעת, יש לנו 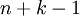 מקומות שצריך למלא (k אחדות ו n-1 חוצצים) וצריך לבחור מתוכם את המקומות של החוצצים (ואז ממילא יקבעו מקומות של האחדות) ולכן יש
מקומות שצריך למלא (k אחדות ו n-1 חוצצים) וצריך לבחור מתוכם את המקומות של החוצצים (ואז ממילא יקבעו מקומות של האחדות) ולכן יש
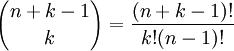 אפשריות כאלו.
אפשריות כאלו.
מסקנה מספר הדרכים שיש לבחור k איברים מתוך קבוצה של n איברים כאשר מותר לי לבצע חזרות ולא משנה הסדר הוא 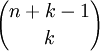
הוכחה
נסמן את האיברים בקבוצה 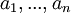 . נסמן את מספר החזרות של כל איבר
. נסמן את מספר החזרות של כל איבר 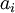 ב-
ב-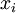 (שלם אי שלילי).
כיוון שרוצים לבחור k איברים השאלה שקולה ל-כמה פתרונות שלמים אי שליליים יש למשוואה
(שלם אי שלילי).
כיוון שרוצים לבחור k איברים השאלה שקולה ל-כמה פתרונות שלמים אי שליליים יש למשוואה 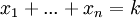 שראינו שהתשובה היא
שראינו שהתשובה היא 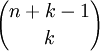
תרגיל ממבחן 2009 מועד א' (ד"ר אלי בגנו וד"ר שי סרוסי)
א. בכמה דרכים ניתן לבחור שני מספרים שונים מ1 עד 100 שסכומם זוגי? הוכח.
- 1.
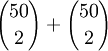
- 2.
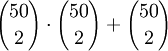
- 3.
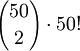
- 4.
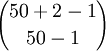
ב. בכמה דרכים ניתן לבחור 3 מספרים שונים מ1 עד 100 שסכומם זוגי? הוכח.
- 1.
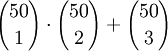
- 2.
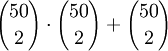
- 3.
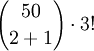
- 4.
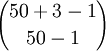
ג. נתונה קבוצה סופית A. נסמן ב-C את קבוצת היחסים על A. מהו מספר הפונקציה החח"ע מC אל A? הוכח.
פתרון.
א. ניתן לבחור כל מספר מ1 עד 100. כעת, המספר המתאים לו צריך להיות מאותה זוגיות על מנת שהסכום יהיה זוגי. לכן בבחירה הראשונה היו לנו 100 אפשרויות ובשנייה 49. כעת, סדר הזוג לא משנה לכן נחלק ב2. סה"כ התוצאה היא 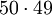 . זה בדיוק שווה לסעיף 1, שכן
. זה בדיוק שווה לסעיף 1, שכן
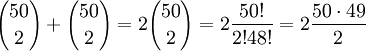
דרך אחרת להסתכל על הפתרון: נבחר 2 זוגיים, או 2 אי-זוגיים.
ב. ניתן לבחור שלושה מספרים זוגיים, או שני אי זוגיים וזוגי. 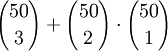
ג. נסמן 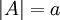 . מספרים היחסים על A הוא קבוצת החזקה של
. מספרים היחסים על A הוא קבוצת החזקה של 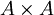 שזה
שזה 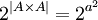 . כעת, פונקציה חד ערכית מקבוצה בגודל k אל קבוצה בגודל n מכילה
. כעת, פונקציה חד ערכית מקבוצה בגודל k אל קבוצה בגודל n מכילה
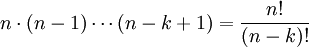 איברים.
איברים.
אבל, חייב להתקיים ש k<n אחרת לא תתכן פונקציה חח"ע (והנוסחא כמובן לא תהא הגיונית), במקרה שלנו 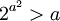 ולכן אין אף פונקציה חח"ע מקבוצת היחסים של A אל A.
ולכן אין אף פונקציה חח"ע מקבוצת היחסים של A אל A.
טבלת סיכום לנוסחאות בסיסיות ידועות
| בעייה | מספר האפשרויות |
| מספר האפשרויות לסדר n אנשים שונים בשורה | 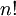
|
| מספר האפשרויות לבחור קבוצה של k תלמידים מתוך כיתה של n תלמידים (ללא משמעות לסדר, ללא חזרות) | 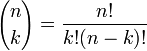
|
| מספר האפשרויות לבנות סדרה עם k איברים מתוך קבוצה המכילה מ איברים (עם משמעות לסדר, ועם חזרות) | 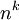
|
| מספר האפשרויות לבנות סדרה עם k איברים שונים מתוך קבוצה המכילה n איברים (עם משמעות לסדר, ללא חזרות) | 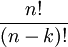
|
| מספר האפשרויות לבחור k איברים מתוך n איברים (ללא משמעות לסדר, עם חזרות) | 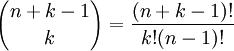
|