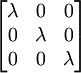הבדלים בין גרסאות בדף "לינארית 2 לתיכוניסטים תש"ע"
(←תשובה) |
(←פתיחת מחברות) |
||
| (206 גרסאות ביניים של 41 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | + | ::<math> | |
\begin{bmatrix} | \begin{bmatrix} | ||
\lambda & 0 & 0 \\ | \lambda & 0 & 0 \\ | ||
| שורה 25: | שורה 25: | ||
'''[[לינארית 2 לתיכוניסטים תש"ע - ארכיון 5|ארכיון 5]]''' - שאלות על המבחן | '''[[לינארית 2 לתיכוניסטים תש"ע - ארכיון 5|ארכיון 5]]''' - שאלות על המבחן | ||
| + | |||
| + | '''[[לינארית 2 לתיכוניסטים תש"ע - ארכיון 6|ארכיון 6]]''' - שאלות על המבחן | ||
= שאלות = | = שאלות = | ||
| + | ==פתיחת מחברות== | ||
| + | מתי יש פתיחת מחברות של מועד ב'? | ||
| + | :תשאלו את המרצים | ||
| + | |||
| + | ==מבחן מועד א'== | ||
| + | העלתם את הפתרונות של מועד א' אבל לא העליתם את המבחן עצמו. | ||
| + | אתם יכולים להעלות את המבחן? | ||
| + | תודה. | ||
| − | |||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | תצלם מאחד החברים, אני אפילו לא בטוח שיש לי אותו | |
| − | + | ||
| − | + | ==פתיחת מחברות== | |
| + | מתי בדיוק תתקיים פתיחת מחברות לקבוצה של ד"ר צבאן? | ||
| + | |||
| + | ==פתרון המבחן-בקשה מהמתרגלים והמרצים== | ||
| + | תוכל לעלות בבקשה את הפתרון למבחן (מועד א'). כך שנוכל לראות בצורה מדוייקת | ||
| + | איך צריך לגשת לשאולות, איך לנסח את הפתרון - והכי חשוב את לפתור את כל השאלות. | ||
| + | זה חשוב גם לאילו שמעוניינים לגשת למועד ב'. | ||
| + | ,תודה רבה. | ||
| + | |||
| + | |||
| + | :פתרון המבחן כבר עלה לפני שבוע. נמצא עם פתרונות התרגילים. | ||
| + | |||
| + | ==ציוני מבחן== | ||
| + | מתי יהיו הציונים בלינארית בערך? | ||
| + | |||
| + | ===תשובה=== | ||
| + | הבדיקה בשלביה האחרונים, אנחנו מקווים שיהיה תוצאות כבר בשבוע הבא | ||
| + | |||
| + | ==מקום הפרסום== | ||
| + | היי ארז. איפה יפורסמו הציונים של המבחן? במידע אישי לסטודנט? | ||
| + | ואתה תוכל בבקשה לפרסם הודעה באתר כשהציונים יפורסמו? תודה! | ||
| + | |||
| + | |||
| + | ===תשובה=== | ||
| + | אני לא יודע, אני אודיע כשאדע | ||
| + | |||
| + | == שאלה == | ||
| + | |||
| + | אהמ, מישהו יודע אם יש מצב להקדים מועד ב' ?? | ||
==שאלה== | ==שאלה== | ||
| − | |||
| − | == | + | אם נתון לי בסיס E וקיימת לי מטריצה אוניטרית P, מותר לי להגדיר בא"נ B כך ש P תיהיה מטריצת המעבר מ B ל E? |
| − | + | ||
| + | ===תשובה=== | ||
| + | כן. כי אם נכפיל בשמאל במטריצה המעבר מE לS הסטנדרטי היא תהיה אוניטרית לכן המכפלה תהיה אוניטרית והמכפלה תהיה מטריצה המעבר מB לS ולכן B בא"נ. | ||
| − | + | == הוכח\הפרך == | |
| + | |||
| + | שאלה מהמבחן של בוריס שנה שעברה, האם מישו הצליח לפתור?- | ||
| + | תהי A מטריצה ממעלה >=2 כך ש-<math>degA=2 <= rkA=1(</math> | ||
===תשובה=== | ===תשובה=== | ||
| − | + | אני הצלחתי להוכיח - אבל אני לא בטוח ב - 100% בנכונות של זה - תנסה לכתוב את A בצורה מפורשת ותעבוד עם זה | |
| + | :גם אני חשבתי ככה (כתבתי את A בתור שורה אחת עם ערכים שאני לא יודע מה הם וכל שאר השורות אפס, ואז הראתי שהפולינום המינימלי על ידי בדיקה הוא באמת ממעלה 2 תמיד), אבל זה ש RANK A = 2 לא בהכרח אומר שלA יש N-1 שורות אפסים, אלא שאפשר להביא אותה לצורה מדורגת כך. לכן הדרך של כתיבה מפורשת לדעתי לא נכונה (ואכן אני לא יודע איך כן להוכיח את זה...). | ||
| − | זה | + | '''תשובה:''' (נכונה) rankA=1 => dimIm(A)=1 ולכן dimKer(A)=n-1 ואז המימד של המרחב העצמי של 0 הוא n-1 (הריבוי הגיאומטרי של 0). מכיוון שהריבוי האלגברי תמיד גדול או שווה לגיאומטרי הוא או N או N-1. אם הוא N אז לפי משפט צורת ז'ורדן יש N-1 בלוקים של 0 אך כל הN עמודות הן של 0 ולכן הבלוק בגודל הכי גדול הוא בגודל 2 ואז M(A)=A^2 כדרוש. אם הוא N-1 אז מכיוון שסכום כל הריבועים האלגבריים הוא N אז יש עוד ערך עצמי עם ריבוי אלגברי (ולכן גם ריבוי גיאומטרי) של 1. לכן לפי משפט צורת ז'ורדן, יש N-1 בלוקים של 0 ו-1 של הערך העצמי הנוסף (נגיד X) ואז הגודל המקסימלי של כל בלוק הוא 1 והפולינום המינימלי הוא M(A)=A(A-X)=> rank(M)=2 מש"ל |
| + | (סליחה שלא כתבתי הכל בכתיב מתמטי אבל אין לי באמת מושג איך..) | ||
| + | |||
| + | == שאלה == | ||
| + | |||
| + | אני יודעת שאתמול הוכחת לנו את זה לפני השיעור חזרה, אבל זה היה ממש לא מסודר ולא ממש הצלחתי לעקוב, אז אני אשמח אם אתה (או מישהו אחר בכיף(:) יתן תשובה: | ||
| + | ככה: T נורמלי הוכח ש- <math>im(T)=im(T^*)</math> | ||
| + | |||
| + | |||
| + | ===הוכחה=== | ||
| + | דבר ראשון נוכיח ש<math>ker(T)=ker(T^*)</math>. נניח <math>v \in kerT</math> לכן <math>Tv=0</math> ולכן <math>\forall u: <T^*Tv,u>=<0,u>=0</math> אבל <math>T^*T=TT^*</math> ולכן <math>\forall u: <TT^*v,u>=0</math> ולכן <math>\forall u: <T^*v,T^*u>=0</math> ובפרט זה נכון עבור v=u ולכן <math><T^*v,T^*v>=0</math> ולכן <math>T^*v=0</math> כלומר <math>v \in ker T^*</math>. בכיוון ההפוך ההוכחה דומה. | ||
| + | |||
| + | |||
| + | עכשיו נוכיח את הטענה. <math>v \in kerT</math> אם"ם <math>\forall u: <Tv,u>=0</math> אם"ם <math>\forall u: <v,T^*u>=0</math> אם"ם <math>v \in (ImT^*)^\bot</math> ולכן <math>kerT = (ImT^*)^\bot</math>. בצורה דומה <math>kerT^*=(ImT)^\bot</math>. אבל הגרעינים שווים ולכן <math>(ImT)^\bot=(ImT^*)^\bot</math> ומזה נובע שהם שווים (כי המרחב המאונך הינו יחיד, והמאונך של המאונך הינו המרחב עצמו). | ||
| + | |||
| + | ==השלמה לבסיס== | ||
| + | האם קיימת דרך בה ניתן להשלים וקטור <math>v_1</math> לבסיס עבור <math>F^n</math> . | ||
| + | למשל שמשלשים וצריך להשלים לבסיס? | ||
| + | |||
| + | ===תשובה=== | ||
| + | זו שאלה מלינארית 1. על מנת להשלים קבוצת וקטורים לבסיס, אתה שם אותם בשורות מטריצה, מדרג אותה, ומוסיף וקטורים שמשלימים את הצירים החסרים. | ||
==שאלה== | ==שאלה== | ||
| − | + | איך מראים שלמטריצה נילפוטנטית יש '''רק''' ע"ע אחד שהוא 0 ? | |
| + | בנוסף, צ"ל שמטריצה משולשת עם אפסים באלכסון היא נילפוטנטית. | ||
| + | אני יכול לומר שהמטריצה דומה לצורת זורדן עם אפסים באלכסון | ||
| + | ומעל אחד-ים ואם נעלה בחזקת K אז נקבל את מט' האפס. איך ממשיכים? | ||
| + | |||
| + | ::הכי פשוט שבעולם - אני הסתכלתי על זה ככה: לפי משפט השילוש, 0 הוא הע"ע היחיד שלה (בהנחה שהאלכסון כולו אפסים), ולכן הפולינום האופייני שלה הוא f(x)=x^n. אם תציב את A תקבל 0, ולכן A^n=0, וזו בדיוק ההגדרה של נילפוטנטית - אם *קיים* k (במקרה זה k=n) עבורו A^k=0. | ||
| + | |||
| + | ===תשובה=== | ||
| + | תשובה לע"ע רק 0-A נילפוטנטנטית מסדר K. נניח שיש ערך עצמי L שהוא לא אפס. ז"א Av=Lv. נכפול משמאל ב-A^K-1 ונקבל 0=LA^k-1V= | ||
| + | אבל A*v= lv ולכן קיבלנו A^k-2*l^2=0. אבל A^K-2 שונה מאפס, וL שונה מאפס ולכן סתירה | ||
| + | |||
| + | ==שאלה== | ||
| + | איך מוכיחים את הכיוון הבא: | ||
| + | אם T אוניטרית אזי היא מעבירה בא"נ לבא"נ אחר (T מעל C) | ||
===תשובה=== | ===תשובה=== | ||
| − | + | צריך להוכיח שאם <math>v_1,...v_n</math> בא"נ אזי גם <math>Tv_1,..Tv_n</math> בא"נ. ההגדרה של בא"נ הינה שהמכפלה הפנימית של כל זוג וקטורים שונים היא אפס, והמכפלה הפנימית של וקטור עם עצמו הינה 1. | |
| − | <math> | + | |
| − | + | T אוניטרית ולכן <math>TT^*=T^*T=I</math>. נבדוק את המכפלה הפנימית של זוג וקטורים בבסיס החדש: | |
| − | + | <math><Tv_i,Tv_j>=<v_i,T^*Tv_j>=<v_i,v_j></math> ולכן המכפלות הן אותו הדבר (ראינו עכשיו שאופרטור אוניטרי שומר מכפלות פנימיות) ולכן גם הבסיס החדש הינו א"נ. | |
==שאלה== | ==שאלה== | ||
| − | + | א. יהי V מ"ו ממימד סופי, יהיא Y(פי) שייך ל- *V ושונה מ-0, יהי W ת"מ של V המכיל את KER Y(פי). צ"ל W=V או W=KER Y | |
| − | : | + | ב. יהי V ממ"פ ממימד סופי. יה Y שייך ל- V* . הוכח כי קיים וקטור W שייך ל- V כך ש: V,W >= ( Y(V> |
| − | + | לכל V שייך ל- V. | |
| − | ( | + | |
| − | + | ||
| − | + | ||
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | א. אתמול בשיעור החזרה הראנו שהמימד של הגרעין של פונקציונל הינו n או n-1 (לפי משפט הדרגה). במקרה שהפונקציונל שונה מאפס המימד של הגרעין הינו n-1. | |
| − | + | אם W מכיל את הגרעין והמימד שלו n-1 אזי הוא שווה לגרעין. אם המימד שלו n אזי הוא שווה למרחב V. אין עוד אופציות כי המימד שלו לא יכול להיות קטן מהמימד של הגרעין אותו הוא מכיל. | |
| − | + | ב. זה משפט ההצגה של ריס. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==שאלה== |
| − | + | איך מראים שכל מטריצה מעל C דומה למטריצה המשוחלפת? A דומה לA^t | |
===תשובה=== | ===תשובה=== | ||
| − | + | בעזרת השאלה ממתחת. A דומה לצורת הז'ורדן שלה <math>A=PJP^{-1}</math> נשחלף לקבל ש | |
| + | <math>A^t=(P^t)^{-1}J^tP^t</math> כלומר A משוחלפת דומה לצורת הז'ורדן המשוחלפת. אבל על ידי החלפת בסיס מתאימה, צורת הז'ורדן המשוחלפת דומה לצורת הז'ורדן ולכן המטריצות דומות. | ||
| + | |||
| + | החלפת הבסיס היא שינוי סדרה איברי הבסיס מהסוף להתחלה, בתוך כל בלוק (נגיד הבלוק הראשון מגודל 3 והשני מגודל 2, אז נחליף לבסיס <math>v_3,v_2,v_1,v_5,v_4</math>. | ||
==שאלה== | ==שאלה== | ||
| − | + | אם אני יודע שה"ל T מעל V ממימד N בהצגה לפי הסטנדרטי היא טראנספוז של בלוק ז'ורדן בגודל NXN, איך אני משנה את הבסיס ככה שהיא תצא בלוק ז'ורדן? | |
===תשובה=== | ===תשובה=== | ||
| − | + | מסדר אותו מהסוף להתחלה. זה שקול למטריצת המעבר עם אחדות באלכסון המשני. מעבר הבסיס יהיה להחליף את סדר השורות ואז להחליף את סדר העמודות | |
| − | + | ==שאלה== | |
| + | הוכח\הפרך: מעל R^n אם T אורתוגונלי וT^2=I אז T סימטרי. | ||
| + | האם המטריצה ההפכית יחידה? כי אם כן | ||
| + | TT=I | ||
| + | TT*=I | ||
| + | ואז T=T* משמע שזה אמת | ||
| − | + | ===תשובה=== | |
| + | בוודאי שההופכית יחידה... | ||
| − | + | וזו הוכחה נכונה. | |
| − | :: | + | :תודה! (: |
| − | + | ||
| + | == 2 שאלות== | ||
| + | 1) ארז תוכל בבקשה להסביר לי למה לכל אופרטור יש בא"נ כך שההצגה שלו לפי הבא"נ הזה היא סכום ישר של סיבובים ו-פלוס-מינוס אחדים? | ||
| + | |||
| + | 2) עברתי על השאלה בנוגע להוכחת תהליך גרם-שמידט ועדיין לא הבנתי את זה. עברתי על ההוכחה שיש בהרצאה וגם שם זה לא ברור לי. תוכל בבקשה להגיד לי מה בעצם מוכיחים ואיך מוכיחים? | ||
| + | |||
| + | תודה! | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | 1. זה נכון רק לאופרטורים א"ג, ולא לכל אופרטור. ההוכחה היא באינדוקציה. אנחנו יודעים מההרצאה שזה נכון לאופרטורים א"ג מעל מרחבים ממימד 2 כי הם סיבובים או שיקופים (ושיקוף הוא מטריצה עם 1 ומינוס אחד על האלכסון). | |
| + | |||
| + | לאופרטורים א"ג מעל מרחבים ממימד גבוה יותר, מפרקים אותם לסכום יש של אופרטורים א"ג מעל מרחב אינווריאנטי מימד 1 או 2, והמרחב הניצב לו, ממימד n-1 או n-2. לפי הנחת האינדוקציה המרחבים האלה הן כבר מהצורה הרצויה. | ||
| + | |||
| + | זה מאד דומה להוכחה שיש בפתרון לתרגילים בנושא אופרטורים אנטי סימטריים. | ||
| + | |||
| + | 2. צ"ל להוכיח שהנוסחא <math>w_i=v_i-\sum_{k=1}^i\frac{<v_i,w_k>}{<w_k,w_k>}w_k</math> נותנת וקטור שונה מאפס שמאונך ל<math>w_1,...,w_{i-1}</math>. על מנת להראות שהוא מאונך אליהם מראים שהמכפלה <math><w_i,w_j>=0</math> לכל <math>j<i</math>. אבל לפי ההנחה, הוקטורים <math>w_1,...,w_{i-1}</math> מאונכים זה לזה, ולכן המכפלה יוצאת | ||
| − | + | <math><w_i,w_j>=<v_i,w_j>-\frac{<v_i,w_j>}{<w_j,w_j>}<w_j,w_j>=0</math> כפי שרצינו. | |
| − | + | ||
| − | + | בנוסף, <math>w_i\neq 0</math> מכיוון שאחרת <math>v_i</math> ת"ל ב<math>v_1,...,v_{i-1}</math> בסתירה לכך שזה היה בסיס מלכתחילה. | |
| − | :: | + | :: תודה רבה! - אבל יש רק דבר אחד שלא הבנתי: בנוגע ל-1, שיקוף אמור להיות ה-Ref. למה אמרת שהוא מטריצה של 1 ו-מינוס 1 על האלכסון? |
| − | ::: | + | :::לכל שיקוף קיים בא"נ כך שהמטריצה של השיקוף לפי הבא"נ הינה <math>\begin{bmatrix}-1 & 0 \\0 & 1\end{bmatrix}</math>. |
| − | :::: | + | ::::עדיין לא הבנתי. הרי שיקוף זאת המטריצה cosa,sina,sina,-cosa. למה הכוונה שאתה אומר שיש בא"נ שלפיו זאת המטריצה 1 0 0 1-? |
| + | ::::: זו המטריצה לפי הבסיס הסטנדרטי. תראה שאלה 7 בארכיון 6. | ||
| + | :::::: אוקי, שוב תודה :) | ||
==שאלה== | ==שאלה== | ||
| − | + | יש שאלת הוכח או הפרך שאני לא מצליח לעלות על הכיוון שלה. אשמח לעזרה... | |
| + | הוכח\הפרך: | ||
| + | |||
| + | 1. לכל מטר' A מרוכבת, I+A*A אינה סינגולרית. | ||
| + | |||
| + | 2. אם k^2 ע"ע של A^2 אזי k ע"ע של A. | ||
| + | |||
| + | תודה לעוזר הנחמד. | ||
===תשובה=== | ===תשובה=== | ||
| − | + | 1. הוכחה: | |
| + | |||
| + | אנחנו יודעים ש<math>A^*A</math> הינה חיובית לחלוטין, נוכיח: דבר ראשון, היא הרמיטית ולכן הע"ע שלה ממשיים. דבר שני, נניח ש <math>\lambda</math> ע"ע של <math>A^*A</math> אזי <math>\lambda<v,v>=<A^*Av,v>=<Av,Av>\geq 0</math> ולכן <math>\lambda \geq 0</math>. | ||
| + | |||
| + | כעת, נניח בשלילה ש<math>I+A^*A</math> סינגולרית כלומר לא הפיכה. לכן בהכרח אפס ע"ע שלה, כלומר <math>|I+A^*A+0\cdot I|=0</math> כלומר, <math>|A^*A-(-1)\cdot I|=0</math> כלומר מינוס אחד הינו ע"ע של <math>A^*A</math> בסתירה לכך שהע"ע שלה הינם חיוביים. | ||
| + | |||
| + | 2. הפרכה: | ||
| + | |||
| + | ניקח A=I. אזי <math>(-1)^2</math> הינו ע"ע של A^2=I אבל מינוס אחד לא ע"ע של A | ||
| + | :תודה רבה רבה רבה | ||
| + | |||
==שאלה== | ==שאלה== | ||
| − | יש | + | בהוכחה למעלה יש לך מעבר לא נכון, מ<A*Av,v> קפצת ל l<v,v< וזה לא נכון.. |
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | שים לב ש<math>\lambda</math> הינו ע"ע של <math>A^*A</math> ולכן <math>A^*Av=\lambda v</math> | |
| − | + | ||
| − | + | ||
| − | ==שאלה | + | ==שאלה== |
| − | + | :עוד שאלה שאני שובר את הראש עליה, עזרה תתקבל בברכה: | |
| − | + | :A מטריצה מרוכבת בגודל 3X3 כך ש: | |
| − | + | :A(A^2+I)(A-2I)=0 | |
| − | + | :הוכח: A לכסינה. | |
| − | + | ||
| − | + | ||
| − | + | תשובה | |
| − | + | זה מתפרק לפולינום שA פותרת אותו: | |
| − | + | x(x-i)(x+i)(x-2) z | |
| − | : | + | אנחנו יודעים שA מרוכבת, לכן הפולינום האופייני שלה מתפרק לגורמים ליניאריים מעל המרוכבים תמיד. |
| + | מלבד זאת, אנחנו יודעים שהפולינום המינימלי של כל מטריצה (בפרט A) מחלק כל פולינום המאפס אותה (את A) | ||
| + | ואם הפולינום המינימלי מחלק את הפולינום הזה ואנחנו יודעים שהוא ממעלה קטנה\שווה 3 לכל מטריצה מסדר 3X3, הוא מהצורה | ||
| + | http://math-wiki.com/images/math/4/0/2/40248c16227e65ef2bce5e5d2056d7bf.png | ||
| + | וזה אם ורק אם A לכסינה | ||
| + | |||
| + | ::איך קטנה שווה 3? לא אמור להיות קטנה שווה ל4? הפולינום הנתון הוא ממעלה 4!! | ||
| + | |||
| + | :: כן אבל הפולינום המינמלי צריך לחלק את הפולינום האופיני כאשר הפ"א הוא ממעלה 3 (תסתכל בהרצאה 2 אם אתה לא זוכר..) ולכן הפולינום המינימלי הוא מדרגה קטנה או שווה ל-3.. | ||
==שאלה== | ==שאלה== | ||
| − | + | שיינר, אם אפשר ליישר קו, מה אומר החלק המתמטי של משפט אוילר, שאותו אנחנו צריכים לדעת? | |
| + | |||
===תשובה=== | ===תשובה=== | ||
| − | + | אני לא יכול לעזור בזה, כיוון שלא ראיתי את המבחן. | |
| − | + | תנסו להבין כמה שאתם יכולים. | |
| − | + | ||
| − | : | + | :אני לא שואל מה יהיה במבחן אני שואל, מבחינת הקורס, מה אומר משפט אוילר. מצדי תן קישור לויקיפדיה |
| − | :: | + | ::אני מבין, אני פשוט אומר שאני לא יודע בדיוק בעצמי מה הכוונה, ולכן לא רוצה לעסוק בניחושים. חפשתי עכשיו קישור למשפט ואני לא מוצא. |
| − | : | + | |
| − | + | אז תחשוב כמה נחמד זה להיות יום לפני מבחן ולא לדעת מה אומר המשפט :) | |
| + | |||
| + | זו שאלה שונה, המשפט אומר שהזזה של גוף צפיד עם נקודת שבת שקולה לסיבוב סביב ציר מסוים. | ||
| + | |||
| + | תודה I GUESS... | ||
==שאלה== | ==שאלה== | ||
| − | + | למה אם 0=(SV,V) לכל V כאשר S אופרטור לינארי צל"ע אז S=0?? | |
| + | *לך לארכיון 5 יש שם תשובה לשאלה ממש דומה ואפילו נראה לי כזאת שמכלילה את זה.. | ||
| − | + | ::(מישהו אחר) הסתכלתי שם וראיתי שאתה גם מוכיח את זה וגם מוכיח שזה לא נכון. אני לא מבין מה ה"תיקון" שהיה שם, הרי זאת אותה השאלה בדיוק..:S | |
| + | ::: סבבה הבנתי, תודה על ההערה. :) | ||
| − | |||
| − | |||
| − | + | ::תקרא שובפעם מה שכתוב שם ותראה שבשאלה הראשונה שנשאלה לא מיקדו אותך מעל איזה שדה זה( R או Cׂ ׂ) ואז יכלת להפריך זאת ע"י דוגמא מעל R אבל כאשר זוהי העתקה מעל C הדוגמא שנתנה בתחילה לא סותרת את זה ובהוכחה גם הוא השתמש בכך שאתה מעל C ... | |
| + | מה שכן- זה באמת לא ממש אותה שאלה, כי פה באמת לא אומרים לך מעל איזה שדה אתה... תנסה לחשוב על זה קצת (: | ||
| − | + | ==שאלה== | |
| + | איך פותרים את סעיף ב' בשאלה הזאת: | ||
| − | + | נתונה מטריצה A: | |
| − | + | 0 0 0 5 | |
| − | + | 0 0 4 1 | |
| − | + | 0 3 3 2 | |
| − | + | 3 6 5 4 | |
| − | + | א) מצא את צורת הז'ורדן של A (צדקת ארז, זה באמת עם ז'.. חחח) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | ב) מצא מטריצה P הפיכה כך ש-p^-1*A*P היא צורת הז'ורדן של A. | ||
| + | תודה! | ||
| − | זה | + | :למדנו בכלל למצוא את הP ההפיכה הזו? אני חושבת שאנחנו לא צריכים לדעת את זה |
| + | ::לא למדנו מטריצה מז'רדנת. לא צריך לדעת. | ||
| + | == שאלה == | ||
| + | איפה המבחן מחר? | ||
| + | לפי אורי וייס | ||
| + | 505 כיתה 2- זה רק הכיתה של בוריס...505 כיתה 1 זה הכיתה של צבאן... | ||
| + | |||
| + | == שאלה == | ||
| + | |||
| + | סתם שאלה, אפשר לראות הוכחה לכך שאם U הוא T אינ' אז גם U+ (הת"מ הנציב) הוא גם T אינ' כאשר T א"ג, אני לא בטוח שהדרך שלי נכונה... | ||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | לא | + | T אורתוגונאלי, ולכן לא מנוון |
| − | + | לכן, לפי משפט הדרגה, IMT=Uכאשר T מצומצם על U+ | |
| + | כלומר לכל w בU קיים w' כך ש T(w')=w | ||
| + | נניח y במרחב הניצב למרחב המקורי | ||
| + | <w,Ty>=<Tw',Ty>=<w',y>=<0> | ||
| + | ולכן Ty גם בU+ | ||
| + | |||
==שאלה== | ==שאלה== | ||
| − | + | האם פונקציה דו לינארית שולחת בהכרח לסקלר? | |
| + | ==תשובה== | ||
| + | לפי ההגדרה f:VxV->F לכן בהכרח סקלר. | ||
| + | |||
| + | ==שאלה== | ||
| + | המרחב הדואלי. כמעט ולא עסקנו בו וגם לא ניתן לנו תרגיל בית. הוא יכול להיות במבחן? | ||
===תשובה=== | ===תשובה=== | ||
| − | + | התעסקנו איתו הרצאה ותרגיל כמו כל נושא. תרגיל בית אכן לא ניתן. כמובן שהוא יכול להופיע במבחן. | |
| − | |||
| − | + | רואים שזה היה במבחן? אסור לפסול חומר... | |
| + | |||
| + | ==שאלה על התרגיל== | ||
| + | קיבלתי בתרגיל 50 ובמבחן 100, סופי 90. יש סיכוי כלשהו להעלות לי את התרגיל? (אני מניח שרוב מי שקורא את זה יודע מי אני...:-) ) | ||
| + | |||
| + | :לא נגשת לבוחן? על סמך מה נעלה את התרגיל? | ||
| + | |||
| + | =תודה!!= | ||
| + | ארז שיינר, תודה רבה לך על כל ההתמסרות וההשקעה בזמן הסמסטר וכמובן לפני המבחן בשאלות שלי ושל כולם. | ||
| + | תבוא לתרגל באינפי 2 (: | ||
| + | |||
| + | : בהחלט כל הכבוד, מסכים עם כל מה שנאמר פה ובאמת שאין דרך לתאר את הרצון שלך לעזור לנו והעזרה שנתת לכולנו | ||
| + | |||
| + | :אין ספק שאתה צריך לתרגל אותנו אינפי 2..חחח | ||
| + | |||
| + | |||
| + | תודה לכם, ומקווה שהלך טוב המבחן. מי שלא, נתראה במועד ב'. | ||
| + | |||
| + | -מצטרף לתשבוחות | ||
| + | רק אם אפשר לתת קצת ביקורת קונסטרוקטיבית: מאגר העניבות מחזורי, וזה מקשה על ההתרכזות בתרגולים, כיוון שבמקום לעסוק במיון שניויניות, אנו הסטדנטים חייבים לחשוב מתי כבר ראינו עניבה מסוימת ולבנות העתקה על בין קבוצת העניבות שלך לתרגולים. לפיכך, הינך מתבקש לרכוש עניבות חדשות ומחושדות, אם אפשר עם ציורים חמודים. תודה מראש | ||
| + | |||
| + | :חחחחחחחחחחחח גדוללל! | ||
| + | |||
| + | :מאיפה אתה קונה את העניבות האלה? גמאני רוצה 8) | ||
| + | |||
| + | חחח תכלס עניבות מגניבות...מתרגל מצוין עם אחלה לוק !!! | ||
| + | |||
| + | =שאלה= | ||
| + | בציוני התרגיל שלי תרגיל שהגשתי וקיבלתי חזרה כתוב שקיבלתי בו 0 למרות שקיבלתי בו 95. | ||
| + | מה לעשות? | ||
| + | |||
| + | ===תשובה=== | ||
| + | אם זה לא משפיע על הציון הסופי, אז להבין שזה לא אומר כלום ולא להציק לי סתם. אם מדובר על תרגיל ש'''ישנה''' את הציון באדום, אפשר לשלוח לי מייל בנושא. | ||
==שאלה== | ==שאלה== | ||
| − | + | היי ארז, | |
| + | ברור לך שהזמן של הבוחן היה קצר מאוד,וסביר להניח שהפעם לרוב ציון התרגיל די מוריד את הממוצע.גם אם זה בשתי נק' זה ממש מבאס,כי על בוחן אי אפשר לעשות מועד ב' ולהוכיח שהנפילה החד פעמית הייתה בגלל חוסר זמן....הנה עבר לו המבחן,וכמו שאמרת מטרת הבוחן הייתה לזעזע אותנו לקראת המבחן....אז מה אתה אומר שעכשיו תנסו(כן גם ניסיון יעזור...) לדון בציון....אולי תעשו כמו ברוב הקורסים הגבוהה מבין ציון התרגילים לבוחן,או תורידו את המשקל של הבוחן? | ||
| + | תודה רבה! | ||
| + | נ.ב:ארז ,אני רוצה בשם כל תלמידי הקורס למסור לך אתת הערכתנו על התמיכה...מקווים שתתרגל אותנו באינפי 2 או באלגברה מופשטת!!!!!!!! | ||
| + | |||
| + | |||
| + | סתם שאלה-מתי מתחיל סמסטר ב'? תודה... | ||
| + | |||
| + | :מתי יפורסמו פתרונות למבחן? | ||
| + | |||
| + | |||
| + | ::אחרי שהמבחנים יבדקו | ||
| + | |||
| + | :::לא מאמינים. תוכיח :) | ||
| + | :::: אני אף פעם לא משקר. אמרתי שאחרי שהמבחנים יבדקו. לכן משפט זה הוא אמת. מ.ש.ל | ||
| + | ==שאלה== | ||
| + | מה מס' הקורס? :P | ||
| + | ==אמירה== | ||
| + | יש ציונים!!! | ||
| + | |||
| + | למה לקבוצה של בועז אין ומתי יהיה? | ||
| + | |||
| + | הם עוד בבדיקה, אני מקווה שיהיה בקרוב. פתרון המבחן נמצא בדף הפתרונות | ||
| + | |||
| + | איך התחלק הניקוד בשאלות ההוכחה בין סעיף א לב? | ||
| + | |||
| + | 18/11 | ||
| + | |||
| + | מה 18 ומה 11 עזוב מספרים שפה קשה כאילו סעיף א-18 וסעיף ב-11? | ||
| + | |||
| + | :כן, מן הסתם ההוכחה שוקלת יותר... | ||
| + | |||
| + | |||
| + | :ארז - יש לי שאלה - במבחן, נניח שמישהו השתמש בטענה שהריבוי האלגברי תמיד יהיה גדול או שווה לריבוי הגיאומטרי בשאלה 1 (א'), מבלי להוכיח את הטענה הזו - האם יורידו נקודות? אם כן, זה יהיה קצת לא הוגן, כי בהוכחה המקורית שיש באתר לאותה שאלה בדיוק (שד"ר צבאן העלה כהשלמה להרצאה) מתייחסים אל אי-השוויון הזה כמובן מאליו. | ||
| + | |||
| + | ::עד כמה שידוע לי לא ירדו נקודות על זה. חכו לפתיחת המחברות | ||
| + | |||
| + | מתי הפתיחת מחברות? | ||
| + | |||
| + | תשאלו את המרצים | ||
| + | |||
| + | ==הכרזה== | ||
| + | יש ציונים! וכן, גם לקבוצה של ד"ר צבאן! (ב'ציוני ביניים') | ||
| + | |||
| + | יכול להיות שהיה פקטור? הציונים נראים לכם סבירים<? | ||
| + | הציונים הרשומים בציוני ביניים ב-ט-ו-ח נכונים? אחרי שרושמם אפשר לשנותם אם לא מגישים ערעור?(כלומר מצד המרצה או משהו) | ||
| + | |||
| + | |||
| + | הממוצע מאד גבוה, אם יהיה פקטור הוא לא יהיה לכיוון שתאהבו :) אבל לא יהיה פקטור כזה כמובן.. | ||
| + | |||
| + | ==שאלה== | ||
| + | מישהו יודע אילו וכמה קורסים צפויים בסמסטר ב' (לא כולל קורסי קיץ)? נשאר לנו השנה (למתמטיקה שימושית) : אינפי 2, שימושי מחשב, אלגברה מופשטת, הסתברות וסטטיסטיקה, ושיטות נומריות. | ||
===תשובה=== | ===תשובה=== | ||
| − | + | את אינפי 2 ושימושי מחשב נלמד בסמסטר ב'. | |
| − | == | + | ==הצעה== |
| − | + | לדעתי יהיה הוגן להחליט שאם ציון המבחן גבוה מציון הבוחן, אז הציון הסופי ייקבע כ-90% מציון המבחן ועוד 10% מציון התרגילים. | |
===תשובה=== | ===תשובה=== | ||
| − | + | ציוני התרגיל הוגנים וציוני המבחן הוגנים מאד. אי אפשר להתחשב בכל החזיתות. | |
| + | |||
| + | :אבל הבוחן ממש לא היה הוגן. היה מחסור חמור בזמן, כל טעות קטנה הובילה לירידה גדולה בציון וגם הבדיקה לא נעשתה ברחמנות, בלשון המעטה. לכן, אם מישהו מעד בבוחן (מה שיכל לקרות בקלות בגלל כל הסיבות שפירטתי למעלה) והוכיח את עצמו אחר כך במבחן, צריך לדעתי להתחשב יותר במבחן על חשבון הבוחן. | ||
| + | |||
| + | ::בדיקת הבוחן הייתה הוגנת, והבוחן היה הוגן. ציון תרגילי הבית היה קרוב ל100 לכולם. מטרת הציון הסופי של הקורס היא לא לחפש סיבות למה לתת לכולם 100. לכל קורס יש כללים מסוימים וחלוקה בין הציונים השונים, והמטרה שלכם היא להצליח בצורה המירבית. אם ניצור נוסחא אישית לכל תלמיד פשוט כולם יקבלו ציונים טובים. השורה התחתונה היא שממוצע הציונים הסופיים גבוה מאד גם ככה, ובוודאי אין מקום לשום התחשבות נוספת. אני מאד מעריך את הרצון והשאיפה לקבל ציונים טובים, ואני ממליץ שתתעלו אותו ללמידה והמשך הצלחה בקורסים הבאים. | ||
| + | |||
| + | מתי יהיו ציונים סופיים? | ||
| + | |||
| + | לא יודע, אבל ניתן לחשב פחות או יותר לבד: 20 אחוז ציון תרגיל (הציון הסופי שפורסם באתר) ו80 אחוז ציון מבחן. | ||
| + | |||
| + | ===פתיחת מחברות=== | ||
| + | מה עם פתיחת המחברות של הקבוצה של בוריס? | ||
| + | |||
| + | |||
| + | אני ממליץ לשאול את בוריס :) | ||
| + | |||
| + | ===לגבי מועד ב'=== | ||
| + | אפשר בבקשה לקבל מידע על מועד ב' (האם אותו מבנה, האם הוא יהיה רק לתיכוניסטים או לכל הסטודנטים, האם יהיה שיעור חזרה לקראתו, האם הוא יהיה יותר קשה)?? | ||
| + | |||
| + | |||
| + | רציתי להצטרף לשואל ולשאול האם גם המתכונת של המבחן תהיה זהה? כלומר כמות השאלות וכו'.. | ||
| + | |||
| + | ===תשובה=== | ||
| + | מומלץ לשאול את המרצים, אבל עד כמה שידוע לי המועד ב' צריך להיות כמו המועד א', כלומר כמו שאמרנו לכם להתכונן למועד א' (כמובן שיכול להופיע חומר שלא היה בפועל במועד א' אבל היה צריך ללמוד אותו במועד א'). | ||
| + | |||
| + | ===תשובה של דר' צבאן=== | ||
| + | לתלמידים עם ציונים מעולים (נאמר, תשעים ומעלה), איני ממליץ לעשות מועד ב'. | ||
| + | |||
| + | לתלמידים עם ציון סופי (כולל תרגיל ובוחן) מתחת לשמונים, אני ממליץ כן לעשות מועד ב', מהסיבה שציון | ||
| + | נמוך משמונים לעתים אינו מוכר לפטור מקורס באוניברסיטאות אחרות, למקרה שתרצו לעבור תחום | ||
| + | ו/או אוניברסיטה. כמובן, זה בתנאי שהתלמיד לוקח את מועד ב' ברצינות ולומד אליו היטב. | ||
| + | |||
| + | לגבי שאר התלמידים: זו החלטה שעליהם לקחת בעצמם, ויש לקחת בחשבון כמה דברים. | ||
| + | |||
| + | סטטיסטית, רוב מי שלומד שוב (היטב) למועד ב', מצליח יותר במועד ב' מאשר במועד א', וגם מבין | ||
| + | את החומר טוב יותר בשביל הקורסים הבאים. כך שזה עשוי להועיל מאד. | ||
| + | מצד שני, תמיד יש יוצאי דופן, וקורה (למרות שנדיר) שתלמיד שניגש שוב ציונו משתנה לרעה. | ||
| + | בכל מקרה, מי שניגש למועד ב', הציון הקובע הוא זה של מועד ב' (לטובה או לא לטובה). | ||
| + | המדיניות שלנו היא להשתדל לעשות מועד ב' ברמה דומה למועד א'. זה עניין סובייקטיבי ובודאי חלק מהתלמידים ירגישו שהוא יותר קל ממועד א', וחלק ירגישו שהוא יותר קשה ממועד א', אבל בפירוש איננו מנסים שהוא יהיה יותר קשה ממועד א'. | ||
| − | + | מידע נוסף, כולל מי צריך להירשם למועד ב' ואיך, תמצאו בקישור הבא (מקורס קיץ ישן): | |
| − | + | http://u.cs.biu.ac.il/~tsaban/Summer08/Summer08.html | |
| − | + | בהצלחה, | |
| − | + | ד"ר בועז צבאן | |
| − | + | : תודה רבה | |
גרסה אחרונה מ־17:16, 2 במאי 2010
תוכן עניינים
- 1 הוראות
- 2 ארכיון
- 3 שאלות
- 3.1 פתיחת מחברות
- 3.2 מבחן מועד א'
- 3.3 פתיחת מחברות
- 3.4 פתרון המבחן-בקשה מהמתרגלים והמרצים
- 3.5 ציוני מבחן
- 3.6 מקום הפרסום
- 3.7 שאלה
- 3.8 שאלה
- 3.9 הוכח\הפרך
- 3.10 שאלה
- 3.11 השלמה לבסיס
- 3.12 שאלה
- 3.13 שאלה
- 3.14 שאלה
- 3.15 שאלה
- 3.16 שאלה
- 3.17 שאלה
- 3.18 2 שאלות
- 3.19 שאלה
- 3.20 שאלה
- 3.21 שאלה
- 3.22 שאלה
- 3.23 שאלה
- 3.24 שאלה
- 3.25 שאלה
- 3.26 שאלה
- 3.27 שאלה
- 3.28 תשובה
- 3.29 שאלה
- 3.30 שאלה על התרגיל
- 4 תודה!!
- 5 שאלה
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחתית הדף את השורה הבאה:
== כותרת שאלה ==
לכתוב מתחתיה את השאלה שלכם, וללחוץ על 'שמירה'.
(אין צורך להרשם לאתר. רק לעקוב אחרי ההוראות הפשוטות...)
ארכיון
ארכיון 1 - שאלות על תרגילים 1-4
ארכיון 2 - שאלות על תרגילים 5-8
ארכיון 3 - שאלות על תרגילים 10-11
ארכיון 4 - שאלות על תרגיל 12 והמבחן
ארכיון 5 - שאלות על המבחן
ארכיון 6 - שאלות על המבחן
שאלות
פתיחת מחברות
מתי יש פתיחת מחברות של מועד ב'?
- תשאלו את המרצים
מבחן מועד א'
העלתם את הפתרונות של מועד א' אבל לא העליתם את המבחן עצמו. אתם יכולים להעלות את המבחן? תודה.
תשובה
תצלם מאחד החברים, אני אפילו לא בטוח שיש לי אותו
פתיחת מחברות
מתי בדיוק תתקיים פתיחת מחברות לקבוצה של ד"ר צבאן?
פתרון המבחן-בקשה מהמתרגלים והמרצים
תוכל לעלות בבקשה את הפתרון למבחן (מועד א'). כך שנוכל לראות בצורה מדוייקת איך צריך לגשת לשאולות, איך לנסח את הפתרון - והכי חשוב את לפתור את כל השאלות. זה חשוב גם לאילו שמעוניינים לגשת למועד ב'.
,תודה רבה.
- פתרון המבחן כבר עלה לפני שבוע. נמצא עם פתרונות התרגילים.
ציוני מבחן
מתי יהיו הציונים בלינארית בערך?
תשובה
הבדיקה בשלביה האחרונים, אנחנו מקווים שיהיה תוצאות כבר בשבוע הבא
מקום הפרסום
היי ארז. איפה יפורסמו הציונים של המבחן? במידע אישי לסטודנט? ואתה תוכל בבקשה לפרסם הודעה באתר כשהציונים יפורסמו? תודה!
תשובה
אני לא יודע, אני אודיע כשאדע
שאלה
אהמ, מישהו יודע אם יש מצב להקדים מועד ב' ??
שאלה
אם נתון לי בסיס E וקיימת לי מטריצה אוניטרית P, מותר לי להגדיר בא"נ B כך ש P תיהיה מטריצת המעבר מ B ל E?
תשובה
כן. כי אם נכפיל בשמאל במטריצה המעבר מE לS הסטנדרטי היא תהיה אוניטרית לכן המכפלה תהיה אוניטרית והמכפלה תהיה מטריצה המעבר מB לS ולכן B בא"נ.
הוכח\הפרך
שאלה מהמבחן של בוריס שנה שעברה, האם מישו הצליח לפתור?-
תהי A מטריצה ממעלה >=2 כך ש-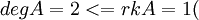
תשובה
אני הצלחתי להוכיח - אבל אני לא בטוח ב - 100% בנכונות של זה - תנסה לכתוב את A בצורה מפורשת ותעבוד עם זה
- גם אני חשבתי ככה (כתבתי את A בתור שורה אחת עם ערכים שאני לא יודע מה הם וכל שאר השורות אפס, ואז הראתי שהפולינום המינימלי על ידי בדיקה הוא באמת ממעלה 2 תמיד), אבל זה ש RANK A = 2 לא בהכרח אומר שלA יש N-1 שורות אפסים, אלא שאפשר להביא אותה לצורה מדורגת כך. לכן הדרך של כתיבה מפורשת לדעתי לא נכונה (ואכן אני לא יודע איך כן להוכיח את זה...).
תשובה: (נכונה) rankA=1 => dimIm(A)=1 ולכן dimKer(A)=n-1 ואז המימד של המרחב העצמי של 0 הוא n-1 (הריבוי הגיאומטרי של 0). מכיוון שהריבוי האלגברי תמיד גדול או שווה לגיאומטרי הוא או N או N-1. אם הוא N אז לפי משפט צורת ז'ורדן יש N-1 בלוקים של 0 אך כל הN עמודות הן של 0 ולכן הבלוק בגודל הכי גדול הוא בגודל 2 ואז M(A)=A^2 כדרוש. אם הוא N-1 אז מכיוון שסכום כל הריבועים האלגבריים הוא N אז יש עוד ערך עצמי עם ריבוי אלגברי (ולכן גם ריבוי גיאומטרי) של 1. לכן לפי משפט צורת ז'ורדן, יש N-1 בלוקים של 0 ו-1 של הערך העצמי הנוסף (נגיד X) ואז הגודל המקסימלי של כל בלוק הוא 1 והפולינום המינימלי הוא M(A)=A(A-X)=> rank(M)=2 מש"ל (סליחה שלא כתבתי הכל בכתיב מתמטי אבל אין לי באמת מושג איך..)
שאלה
אני יודעת שאתמול הוכחת לנו את זה לפני השיעור חזרה, אבל זה היה ממש לא מסודר ולא ממש הצלחתי לעקוב, אז אני אשמח אם אתה (או מישהו אחר בכיף(:) יתן תשובה:
ככה: T נורמלי הוכח ש- 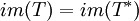
הוכחה
דבר ראשון נוכיח ש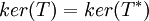 . נניח
. נניח 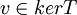 לכן
לכן 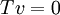 ולכן
ולכן 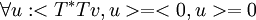 אבל
אבל 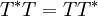 ולכן
ולכן 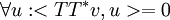 ולכן
ולכן 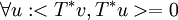 ובפרט זה נכון עבור v=u ולכן
ובפרט זה נכון עבור v=u ולכן 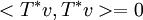 ולכן
ולכן 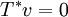 כלומר
כלומר 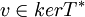 . בכיוון ההפוך ההוכחה דומה.
. בכיוון ההפוך ההוכחה דומה.
עכשיו נוכיח את הטענה. 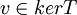 אם"ם
אם"ם 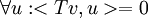 אם"ם
אם"ם 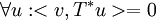 אם"ם
אם"ם 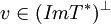 ולכן
ולכן 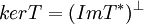 . בצורה דומה
. בצורה דומה 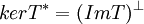 . אבל הגרעינים שווים ולכן
. אבל הגרעינים שווים ולכן 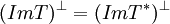 ומזה נובע שהם שווים (כי המרחב המאונך הינו יחיד, והמאונך של המאונך הינו המרחב עצמו).
ומזה נובע שהם שווים (כי המרחב המאונך הינו יחיד, והמאונך של המאונך הינו המרחב עצמו).
השלמה לבסיס
האם קיימת דרך בה ניתן להשלים וקטור 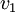 לבסיס עבור
לבסיס עבור 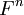 .
למשל שמשלשים וצריך להשלים לבסיס?
.
למשל שמשלשים וצריך להשלים לבסיס?
תשובה
זו שאלה מלינארית 1. על מנת להשלים קבוצת וקטורים לבסיס, אתה שם אותם בשורות מטריצה, מדרג אותה, ומוסיף וקטורים שמשלימים את הצירים החסרים.
שאלה
איך מראים שלמטריצה נילפוטנטית יש רק ע"ע אחד שהוא 0 ? בנוסף, צ"ל שמטריצה משולשת עם אפסים באלכסון היא נילפוטנטית. אני יכול לומר שהמטריצה דומה לצורת זורדן עם אפסים באלכסון ומעל אחד-ים ואם נעלה בחזקת K אז נקבל את מט' האפס. איך ממשיכים?
- הכי פשוט שבעולם - אני הסתכלתי על זה ככה: לפי משפט השילוש, 0 הוא הע"ע היחיד שלה (בהנחה שהאלכסון כולו אפסים), ולכן הפולינום האופייני שלה הוא f(x)=x^n. אם תציב את A תקבל 0, ולכן A^n=0, וזו בדיוק ההגדרה של נילפוטנטית - אם *קיים* k (במקרה זה k=n) עבורו A^k=0.
תשובה
תשובה לע"ע רק 0-A נילפוטנטנטית מסדר K. נניח שיש ערך עצמי L שהוא לא אפס. ז"א Av=Lv. נכפול משמאל ב-A^K-1 ונקבל 0=LA^k-1V= אבל A*v= lv ולכן קיבלנו A^k-2*l^2=0. אבל A^K-2 שונה מאפס, וL שונה מאפס ולכן סתירה
שאלה
איך מוכיחים את הכיוון הבא: אם T אוניטרית אזי היא מעבירה בא"נ לבא"נ אחר (T מעל C)
תשובה
צריך להוכיח שאם 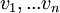 בא"נ אזי גם
בא"נ אזי גם 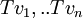 בא"נ. ההגדרה של בא"נ הינה שהמכפלה הפנימית של כל זוג וקטורים שונים היא אפס, והמכפלה הפנימית של וקטור עם עצמו הינה 1.
בא"נ. ההגדרה של בא"נ הינה שהמכפלה הפנימית של כל זוג וקטורים שונים היא אפס, והמכפלה הפנימית של וקטור עם עצמו הינה 1.
T אוניטרית ולכן 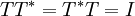 . נבדוק את המכפלה הפנימית של זוג וקטורים בבסיס החדש:
. נבדוק את המכפלה הפנימית של זוג וקטורים בבסיס החדש:
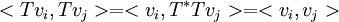 ולכן המכפלות הן אותו הדבר (ראינו עכשיו שאופרטור אוניטרי שומר מכפלות פנימיות) ולכן גם הבסיס החדש הינו א"נ.
ולכן המכפלות הן אותו הדבר (ראינו עכשיו שאופרטור אוניטרי שומר מכפלות פנימיות) ולכן גם הבסיס החדש הינו א"נ.
שאלה
א. יהי V מ"ו ממימד סופי, יהיא Y(פי) שייך ל- *V ושונה מ-0, יהי W ת"מ של V המכיל את KER Y(פי). צ"ל W=V או W=KER Y
ב. יהי V ממ"פ ממימד סופי. יה Y שייך ל- V* . הוכח כי קיים וקטור W שייך ל- V כך ש: V,W >= ( Y(V> לכל V שייך ל- V.
תשובה
א. אתמול בשיעור החזרה הראנו שהמימד של הגרעין של פונקציונל הינו n או n-1 (לפי משפט הדרגה). במקרה שהפונקציונל שונה מאפס המימד של הגרעין הינו n-1.
אם W מכיל את הגרעין והמימד שלו n-1 אזי הוא שווה לגרעין. אם המימד שלו n אזי הוא שווה למרחב V. אין עוד אופציות כי המימד שלו לא יכול להיות קטן מהמימד של הגרעין אותו הוא מכיל.
ב. זה משפט ההצגה של ריס.
שאלה
איך מראים שכל מטריצה מעל C דומה למטריצה המשוחלפת? A דומה לA^t
תשובה
בעזרת השאלה ממתחת. A דומה לצורת הז'ורדן שלה 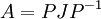 נשחלף לקבל ש
נשחלף לקבל ש
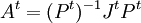 כלומר A משוחלפת דומה לצורת הז'ורדן המשוחלפת. אבל על ידי החלפת בסיס מתאימה, צורת הז'ורדן המשוחלפת דומה לצורת הז'ורדן ולכן המטריצות דומות.
כלומר A משוחלפת דומה לצורת הז'ורדן המשוחלפת. אבל על ידי החלפת בסיס מתאימה, צורת הז'ורדן המשוחלפת דומה לצורת הז'ורדן ולכן המטריצות דומות.
החלפת הבסיס היא שינוי סדרה איברי הבסיס מהסוף להתחלה, בתוך כל בלוק (נגיד הבלוק הראשון מגודל 3 והשני מגודל 2, אז נחליף לבסיס 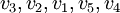 .
.
שאלה
אם אני יודע שה"ל T מעל V ממימד N בהצגה לפי הסטנדרטי היא טראנספוז של בלוק ז'ורדן בגודל NXN, איך אני משנה את הבסיס ככה שהיא תצא בלוק ז'ורדן?
תשובה
מסדר אותו מהסוף להתחלה. זה שקול למטריצת המעבר עם אחדות באלכסון המשני. מעבר הבסיס יהיה להחליף את סדר השורות ואז להחליף את סדר העמודות
שאלה
הוכח\הפרך: מעל R^n אם T אורתוגונלי וT^2=I אז T סימטרי. האם המטריצה ההפכית יחידה? כי אם כן TT=I TT*=I ואז T=T* משמע שזה אמת
תשובה
בוודאי שההופכית יחידה...
וזו הוכחה נכונה.
- תודה! (:
2 שאלות
1) ארז תוכל בבקשה להסביר לי למה לכל אופרטור יש בא"נ כך שההצגה שלו לפי הבא"נ הזה היא סכום ישר של סיבובים ו-פלוס-מינוס אחדים?
2) עברתי על השאלה בנוגע להוכחת תהליך גרם-שמידט ועדיין לא הבנתי את זה. עברתי על ההוכחה שיש בהרצאה וגם שם זה לא ברור לי. תוכל בבקשה להגיד לי מה בעצם מוכיחים ואיך מוכיחים?
תודה!
תשובה
1. זה נכון רק לאופרטורים א"ג, ולא לכל אופרטור. ההוכחה היא באינדוקציה. אנחנו יודעים מההרצאה שזה נכון לאופרטורים א"ג מעל מרחבים ממימד 2 כי הם סיבובים או שיקופים (ושיקוף הוא מטריצה עם 1 ומינוס אחד על האלכסון).
לאופרטורים א"ג מעל מרחבים ממימד גבוה יותר, מפרקים אותם לסכום יש של אופרטורים א"ג מעל מרחב אינווריאנטי מימד 1 או 2, והמרחב הניצב לו, ממימד n-1 או n-2. לפי הנחת האינדוקציה המרחבים האלה הן כבר מהצורה הרצויה.
זה מאד דומה להוכחה שיש בפתרון לתרגילים בנושא אופרטורים אנטי סימטריים.
2. צ"ל להוכיח שהנוסחא 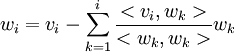 נותנת וקטור שונה מאפס שמאונך ל
נותנת וקטור שונה מאפס שמאונך ל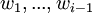 . על מנת להראות שהוא מאונך אליהם מראים שהמכפלה
. על מנת להראות שהוא מאונך אליהם מראים שהמכפלה 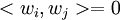 לכל
לכל 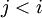 . אבל לפי ההנחה, הוקטורים
. אבל לפי ההנחה, הוקטורים 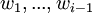 מאונכים זה לזה, ולכן המכפלה יוצאת
מאונכים זה לזה, ולכן המכפלה יוצאת
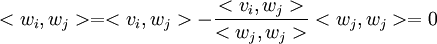 כפי שרצינו.
כפי שרצינו.
בנוסף, 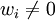 מכיוון שאחרת
מכיוון שאחרת 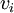 ת"ל ב
ת"ל ב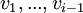 בסתירה לכך שזה היה בסיס מלכתחילה.
בסתירה לכך שזה היה בסיס מלכתחילה.
- תודה רבה! - אבל יש רק דבר אחד שלא הבנתי: בנוגע ל-1, שיקוף אמור להיות ה-Ref. למה אמרת שהוא מטריצה של 1 ו-מינוס 1 על האלכסון?
- לכל שיקוף קיים בא"נ כך שהמטריצה של השיקוף לפי הבא"נ הינה
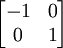 .
.
- לכל שיקוף קיים בא"נ כך שהמטריצה של השיקוף לפי הבא"נ הינה
- עדיין לא הבנתי. הרי שיקוף זאת המטריצה cosa,sina,sina,-cosa. למה הכוונה שאתה אומר שיש בא"נ שלפיו זאת המטריצה 1 0 0 1-?
- זו המטריצה לפי הבסיס הסטנדרטי. תראה שאלה 7 בארכיון 6.
- אוקי, שוב תודה :)
- זו המטריצה לפי הבסיס הסטנדרטי. תראה שאלה 7 בארכיון 6.
- עדיין לא הבנתי. הרי שיקוף זאת המטריצה cosa,sina,sina,-cosa. למה הכוונה שאתה אומר שיש בא"נ שלפיו זאת המטריצה 1 0 0 1-?
שאלה
יש שאלת הוכח או הפרך שאני לא מצליח לעלות על הכיוון שלה. אשמח לעזרה... הוכח\הפרך:
1. לכל מטר' A מרוכבת, I+A*A אינה סינגולרית.
2. אם k^2 ע"ע של A^2 אזי k ע"ע של A.
תודה לעוזר הנחמד.
תשובה
1. הוכחה:
אנחנו יודעים ש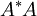 הינה חיובית לחלוטין, נוכיח: דבר ראשון, היא הרמיטית ולכן הע"ע שלה ממשיים. דבר שני, נניח ש
הינה חיובית לחלוטין, נוכיח: דבר ראשון, היא הרמיטית ולכן הע"ע שלה ממשיים. דבר שני, נניח ש  ע"ע של
ע"ע של 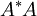 אזי
אזי 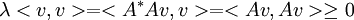 ולכן
ולכן 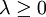 .
.
כעת, נניח בשלילה ש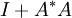 סינגולרית כלומר לא הפיכה. לכן בהכרח אפס ע"ע שלה, כלומר
סינגולרית כלומר לא הפיכה. לכן בהכרח אפס ע"ע שלה, כלומר 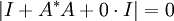 כלומר,
כלומר, 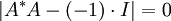 כלומר מינוס אחד הינו ע"ע של
כלומר מינוס אחד הינו ע"ע של 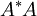 בסתירה לכך שהע"ע שלה הינם חיוביים.
בסתירה לכך שהע"ע שלה הינם חיוביים.
2. הפרכה:
ניקח A=I. אזי 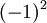 הינו ע"ע של A^2=I אבל מינוס אחד לא ע"ע של A
הינו ע"ע של A^2=I אבל מינוס אחד לא ע"ע של A
- תודה רבה רבה רבה
שאלה
בהוכחה למעלה יש לך מעבר לא נכון, מ<A*Av,v> קפצת ל l<v,v< וזה לא נכון..
תשובה
שים לב ש הינו ע"ע של
הינו ע"ע של 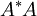 ולכן
ולכן 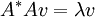
שאלה
- עוד שאלה שאני שובר את הראש עליה, עזרה תתקבל בברכה:
- A מטריצה מרוכבת בגודל 3X3 כך ש:
- A(A^2+I)(A-2I)=0
- הוכח: A לכסינה.
תשובה
זה מתפרק לפולינום שA פותרת אותו:
x(x-i)(x+i)(x-2) z
אנחנו יודעים שA מרוכבת, לכן הפולינום האופייני שלה מתפרק לגורמים ליניאריים מעל המרוכבים תמיד.
מלבד זאת, אנחנו יודעים שהפולינום המינימלי של כל מטריצה (בפרט A) מחלק כל פולינום המאפס אותה (את A)
ואם הפולינום המינימלי מחלק את הפולינום הזה ואנחנו יודעים שהוא ממעלה קטנה\שווה 3 לכל מטריצה מסדר 3X3, הוא מהצורה
http://math-wiki.com/images/math/4/0/2/40248c16227e65ef2bce5e5d2056d7bf.png
וזה אם ורק אם A לכסינה
- איך קטנה שווה 3? לא אמור להיות קטנה שווה ל4? הפולינום הנתון הוא ממעלה 4!!
- כן אבל הפולינום המינמלי צריך לחלק את הפולינום האופיני כאשר הפ"א הוא ממעלה 3 (תסתכל בהרצאה 2 אם אתה לא זוכר..) ולכן הפולינום המינימלי הוא מדרגה קטנה או שווה ל-3..
שאלה
שיינר, אם אפשר ליישר קו, מה אומר החלק המתמטי של משפט אוילר, שאותו אנחנו צריכים לדעת?
תשובה
אני לא יכול לעזור בזה, כיוון שלא ראיתי את המבחן.
תנסו להבין כמה שאתם יכולים.
- אני לא שואל מה יהיה במבחן אני שואל, מבחינת הקורס, מה אומר משפט אוילר. מצדי תן קישור לויקיפדיה
- אני מבין, אני פשוט אומר שאני לא יודע בדיוק בעצמי מה הכוונה, ולכן לא רוצה לעסוק בניחושים. חפשתי עכשיו קישור למשפט ואני לא מוצא.
אז תחשוב כמה נחמד זה להיות יום לפני מבחן ולא לדעת מה אומר המשפט :)
זו שאלה שונה, המשפט אומר שהזזה של גוף צפיד עם נקודת שבת שקולה לסיבוב סביב ציר מסוים.
תודה I GUESS...
שאלה
למה אם 0=(SV,V) לכל V כאשר S אופרטור לינארי צל"ע אז S=0??
*לך לארכיון 5 יש שם תשובה לשאלה ממש דומה ואפילו נראה לי כזאת שמכלילה את זה..
- (מישהו אחר) הסתכלתי שם וראיתי שאתה גם מוכיח את זה וגם מוכיח שזה לא נכון. אני לא מבין מה ה"תיקון" שהיה שם, הרי זאת אותה השאלה בדיוק..:S
- סבבה הבנתי, תודה על ההערה. :)
- (מישהו אחר) הסתכלתי שם וראיתי שאתה גם מוכיח את זה וגם מוכיח שזה לא נכון. אני לא מבין מה ה"תיקון" שהיה שם, הרי זאת אותה השאלה בדיוק..:S
- תקרא שובפעם מה שכתוב שם ותראה שבשאלה הראשונה שנשאלה לא מיקדו אותך מעל איזה שדה זה( R או Cׂ ׂ) ואז יכלת להפריך זאת ע"י דוגמא מעל R אבל כאשר זוהי העתקה מעל C הדוגמא שנתנה בתחילה לא סותרת את זה ובהוכחה גם הוא השתמש בכך שאתה מעל C ...
מה שכן- זה באמת לא ממש אותה שאלה, כי פה באמת לא אומרים לך מעל איזה שדה אתה... תנסה לחשוב על זה קצת (:
שאלה
איך פותרים את סעיף ב' בשאלה הזאת:
נתונה מטריצה A:
0 0 0 5
0 0 4 1
0 3 3 2
3 6 5 4
א) מצא את צורת הז'ורדן של A (צדקת ארז, זה באמת עם ז'.. חחח)
ב) מצא מטריצה P הפיכה כך ש-p^-1*A*P היא צורת הז'ורדן של A. תודה!
- למדנו בכלל למצוא את הP ההפיכה הזו? אני חושבת שאנחנו לא צריכים לדעת את זה
- לא למדנו מטריצה מז'רדנת. לא צריך לדעת.
שאלה
איפה המבחן מחר?
לפי אורי וייס 505 כיתה 2- זה רק הכיתה של בוריס...505 כיתה 1 זה הכיתה של צבאן...
שאלה
סתם שאלה, אפשר לראות הוכחה לכך שאם U הוא T אינ' אז גם U+ (הת"מ הנציב) הוא גם T אינ' כאשר T א"ג, אני לא בטוח שהדרך שלי נכונה...
תשובה
T אורתוגונאלי, ולכן לא מנוון לכן, לפי משפט הדרגה, IMT=Uכאשר T מצומצם על U+ כלומר לכל w בU קיים w' כך ש T(w')=w נניח y במרחב הניצב למרחב המקורי <w,Ty>=<Tw',Ty>=<w',y>=<0> ולכן Ty גם בU+
שאלה
האם פונקציה דו לינארית שולחת בהכרח לסקלר?
תשובה
לפי ההגדרה f:VxV->F לכן בהכרח סקלר.
שאלה
המרחב הדואלי. כמעט ולא עסקנו בו וגם לא ניתן לנו תרגיל בית. הוא יכול להיות במבחן?
תשובה
התעסקנו איתו הרצאה ותרגיל כמו כל נושא. תרגיל בית אכן לא ניתן. כמובן שהוא יכול להופיע במבחן.
רואים שזה היה במבחן? אסור לפסול חומר...
שאלה על התרגיל
קיבלתי בתרגיל 50 ובמבחן 100, סופי 90. יש סיכוי כלשהו להעלות לי את התרגיל? (אני מניח שרוב מי שקורא את זה יודע מי אני...:-) )
- לא נגשת לבוחן? על סמך מה נעלה את התרגיל?
תודה!!
ארז שיינר, תודה רבה לך על כל ההתמסרות וההשקעה בזמן הסמסטר וכמובן לפני המבחן בשאלות שלי ושל כולם. תבוא לתרגל באינפי 2 (:
- בהחלט כל הכבוד, מסכים עם כל מה שנאמר פה ובאמת שאין דרך לתאר את הרצון שלך לעזור לנו והעזרה שנתת לכולנו
- אין ספק שאתה צריך לתרגל אותנו אינפי 2..חחח
תודה לכם, ומקווה שהלך טוב המבחן. מי שלא, נתראה במועד ב'.
-מצטרף לתשבוחות רק אם אפשר לתת קצת ביקורת קונסטרוקטיבית: מאגר העניבות מחזורי, וזה מקשה על ההתרכזות בתרגולים, כיוון שבמקום לעסוק במיון שניויניות, אנו הסטדנטים חייבים לחשוב מתי כבר ראינו עניבה מסוימת ולבנות העתקה על בין קבוצת העניבות שלך לתרגולים. לפיכך, הינך מתבקש לרכוש עניבות חדשות ומחושדות, אם אפשר עם ציורים חמודים. תודה מראש
- חחחחחחחחחחחח גדוללל!
- מאיפה אתה קונה את העניבות האלה? גמאני רוצה 8)
חחח תכלס עניבות מגניבות...מתרגל מצוין עם אחלה לוק !!!
שאלה
בציוני התרגיל שלי תרגיל שהגשתי וקיבלתי חזרה כתוב שקיבלתי בו 0 למרות שקיבלתי בו 95. מה לעשות?
תשובה
אם זה לא משפיע על הציון הסופי, אז להבין שזה לא אומר כלום ולא להציק לי סתם. אם מדובר על תרגיל שישנה את הציון באדום, אפשר לשלוח לי מייל בנושא.
שאלה
היי ארז, ברור לך שהזמן של הבוחן היה קצר מאוד,וסביר להניח שהפעם לרוב ציון התרגיל די מוריד את הממוצע.גם אם זה בשתי נק' זה ממש מבאס,כי על בוחן אי אפשר לעשות מועד ב' ולהוכיח שהנפילה החד פעמית הייתה בגלל חוסר זמן....הנה עבר לו המבחן,וכמו שאמרת מטרת הבוחן הייתה לזעזע אותנו לקראת המבחן....אז מה אתה אומר שעכשיו תנסו(כן גם ניסיון יעזור...) לדון בציון....אולי תעשו כמו ברוב הקורסים הגבוהה מבין ציון התרגילים לבוחן,או תורידו את המשקל של הבוחן? תודה רבה! נ.ב:ארז ,אני רוצה בשם כל תלמידי הקורס למסור לך אתת הערכתנו על התמיכה...מקווים שתתרגל אותנו באינפי 2 או באלגברה מופשטת!!!!!!!!
סתם שאלה-מתי מתחיל סמסטר ב'? תודה...
- מתי יפורסמו פתרונות למבחן?
- אחרי שהמבחנים יבדקו
- לא מאמינים. תוכיח :)
- אני אף פעם לא משקר. אמרתי שאחרי שהמבחנים יבדקו. לכן משפט זה הוא אמת. מ.ש.ל
- לא מאמינים. תוכיח :)
שאלה
מה מס' הקורס? :P
אמירה
יש ציונים!!!
למה לקבוצה של בועז אין ומתי יהיה?
הם עוד בבדיקה, אני מקווה שיהיה בקרוב. פתרון המבחן נמצא בדף הפתרונות
איך התחלק הניקוד בשאלות ההוכחה בין סעיף א לב?
18/11
מה 18 ומה 11 עזוב מספרים שפה קשה כאילו סעיף א-18 וסעיף ב-11?
- כן, מן הסתם ההוכחה שוקלת יותר...
- ארז - יש לי שאלה - במבחן, נניח שמישהו השתמש בטענה שהריבוי האלגברי תמיד יהיה גדול או שווה לריבוי הגיאומטרי בשאלה 1 (א'), מבלי להוכיח את הטענה הזו - האם יורידו נקודות? אם כן, זה יהיה קצת לא הוגן, כי בהוכחה המקורית שיש באתר לאותה שאלה בדיוק (שד"ר צבאן העלה כהשלמה להרצאה) מתייחסים אל אי-השוויון הזה כמובן מאליו.
- עד כמה שידוע לי לא ירדו נקודות על זה. חכו לפתיחת המחברות
מתי הפתיחת מחברות?
תשאלו את המרצים
הכרזה
יש ציונים! וכן, גם לקבוצה של ד"ר צבאן! (ב'ציוני ביניים')
יכול להיות שהיה פקטור? הציונים נראים לכם סבירים<? הציונים הרשומים בציוני ביניים ב-ט-ו-ח נכונים? אחרי שרושמם אפשר לשנותם אם לא מגישים ערעור?(כלומר מצד המרצה או משהו)
הממוצע מאד גבוה, אם יהיה פקטור הוא לא יהיה לכיוון שתאהבו :) אבל לא יהיה פקטור כזה כמובן..
שאלה
מישהו יודע אילו וכמה קורסים צפויים בסמסטר ב' (לא כולל קורסי קיץ)? נשאר לנו השנה (למתמטיקה שימושית) : אינפי 2, שימושי מחשב, אלגברה מופשטת, הסתברות וסטטיסטיקה, ושיטות נומריות.
תשובה
את אינפי 2 ושימושי מחשב נלמד בסמסטר ב'.
הצעה
לדעתי יהיה הוגן להחליט שאם ציון המבחן גבוה מציון הבוחן, אז הציון הסופי ייקבע כ-90% מציון המבחן ועוד 10% מציון התרגילים.
תשובה
ציוני התרגיל הוגנים וציוני המבחן הוגנים מאד. אי אפשר להתחשב בכל החזיתות.
- אבל הבוחן ממש לא היה הוגן. היה מחסור חמור בזמן, כל טעות קטנה הובילה לירידה גדולה בציון וגם הבדיקה לא נעשתה ברחמנות, בלשון המעטה. לכן, אם מישהו מעד בבוחן (מה שיכל לקרות בקלות בגלל כל הסיבות שפירטתי למעלה) והוכיח את עצמו אחר כך במבחן, צריך לדעתי להתחשב יותר במבחן על חשבון הבוחן.
- בדיקת הבוחן הייתה הוגנת, והבוחן היה הוגן. ציון תרגילי הבית היה קרוב ל100 לכולם. מטרת הציון הסופי של הקורס היא לא לחפש סיבות למה לתת לכולם 100. לכל קורס יש כללים מסוימים וחלוקה בין הציונים השונים, והמטרה שלכם היא להצליח בצורה המירבית. אם ניצור נוסחא אישית לכל תלמיד פשוט כולם יקבלו ציונים טובים. השורה התחתונה היא שממוצע הציונים הסופיים גבוה מאד גם ככה, ובוודאי אין מקום לשום התחשבות נוספת. אני מאד מעריך את הרצון והשאיפה לקבל ציונים טובים, ואני ממליץ שתתעלו אותו ללמידה והמשך הצלחה בקורסים הבאים.
מתי יהיו ציונים סופיים?
לא יודע, אבל ניתן לחשב פחות או יותר לבד: 20 אחוז ציון תרגיל (הציון הסופי שפורסם באתר) ו80 אחוז ציון מבחן.
פתיחת מחברות
מה עם פתיחת המחברות של הקבוצה של בוריס?
אני ממליץ לשאול את בוריס :)
לגבי מועד ב'
אפשר בבקשה לקבל מידע על מועד ב' (האם אותו מבנה, האם הוא יהיה רק לתיכוניסטים או לכל הסטודנטים, האם יהיה שיעור חזרה לקראתו, האם הוא יהיה יותר קשה)??
רציתי להצטרף לשואל ולשאול האם גם המתכונת של המבחן תהיה זהה? כלומר כמות השאלות וכו'..
תשובה
מומלץ לשאול את המרצים, אבל עד כמה שידוע לי המועד ב' צריך להיות כמו המועד א', כלומר כמו שאמרנו לכם להתכונן למועד א' (כמובן שיכול להופיע חומר שלא היה בפועל במועד א' אבל היה צריך ללמוד אותו במועד א').
תשובה של דר' צבאן
לתלמידים עם ציונים מעולים (נאמר, תשעים ומעלה), איני ממליץ לעשות מועד ב'.
לתלמידים עם ציון סופי (כולל תרגיל ובוחן) מתחת לשמונים, אני ממליץ כן לעשות מועד ב', מהסיבה שציון נמוך משמונים לעתים אינו מוכר לפטור מקורס באוניברסיטאות אחרות, למקרה שתרצו לעבור תחום ו/או אוניברסיטה. כמובן, זה בתנאי שהתלמיד לוקח את מועד ב' ברצינות ולומד אליו היטב.
לגבי שאר התלמידים: זו החלטה שעליהם לקחת בעצמם, ויש לקחת בחשבון כמה דברים.
סטטיסטית, רוב מי שלומד שוב (היטב) למועד ב', מצליח יותר במועד ב' מאשר במועד א', וגם מבין את החומר טוב יותר בשביל הקורסים הבאים. כך שזה עשוי להועיל מאד. מצד שני, תמיד יש יוצאי דופן, וקורה (למרות שנדיר) שתלמיד שניגש שוב ציונו משתנה לרעה. בכל מקרה, מי שניגש למועד ב', הציון הקובע הוא זה של מועד ב' (לטובה או לא לטובה). המדיניות שלנו היא להשתדל לעשות מועד ב' ברמה דומה למועד א'. זה עניין סובייקטיבי ובודאי חלק מהתלמידים ירגישו שהוא יותר קל ממועד א', וחלק ירגישו שהוא יותר קשה ממועד א', אבל בפירוש איננו מנסים שהוא יהיה יותר קשה ממועד א'.
מידע נוסף, כולל מי צריך להירשם למועד ב' ואיך, תמצאו בקישור הבא (מקורס קיץ ישן):
http://u.cs.biu.ac.il/~tsaban/Summer08/Summer08.html
בהצלחה,
ד"ר בועז צבאן
- תודה רבה