הבדלים בין גרסאות בדף "אלגוריתם ללכסון מטריצה"
(←מציאת מרחבים עצמיים של הערכים העצמיים) |
|||
| (13 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | תהי מטריצה A. נרצה | + | תהי נתונה מטריצה <math>A</math>. נרצה לבדוק האם היא לכסינה, ואם כן - למצוא מטריצה שמלכסנת אותה. |
===מציאת פולינום אופייני=== | ===מציאת פולינום אופייני=== | ||
| − | <math> | + | <math>p_A(x):=\left|xI-A\right|</math>. |
| − | === | + | ===מציאת הערכים העצמיים של המטריצה וריבויים האלגברי=== |
| − | + | <math>\lambda</math> ערך עצמי של <math>A</math> אם ורק אם <math>p_A(\lambda)=0</math>. | |
| − | + | לכל שורש <math>\lambda</math> של <math>p_A(x)</math>, נוציא מהפולינום גורם <math>(x-\lambda)</math>, | |
| + | עד שנגיע למצב | ||
| + | <math>p_A(x)=(x-\lambda_1)^{r_1}\cdots(x-\lambda_k)^{r_k}</math>. | ||
| − | + | '''אם נותר בפולינום גורם שאינו מתפרק לגורמים לינאריים כאלה, אז המטריצה אינה לכסינה''' ואפשר לעצור כאן. | |
| − | + | ||
| + | <math>\lambda_1,\dots,\lambda_k</math> הם הערכים העצמיים השונים של <math>A</math>, | ||
| + | ו | ||
| + | <math>r_1,\dots,r_k</math> | ||
| + | הם הריבויים האלגבריים שלהם, בהתאמה. | ||
| − | + | ===מציאת בסיסים למרחבים העצמיים=== | |
| + | לכל ערך עצמי <math>\lambda</math> של <math>A</math>, מחשבים את המרחב העצמי | ||
| + | <math>V_\lambda:=\left\{v\in \mathbb{F}^n : Av=\lambda v\right\}=N(A-\lambda I)</math>, | ||
| + | אוסף הפתרונות של המערכת ההומוגנית המתאימה למטריצה <math>A-\lambda I</math>. | ||
| − | + | מוצאים בסיס עבור מרחב זה. אם בבסיס יש פחות איברים מהריבוי האלגברי של <math>\lambda</math>, | |
| + | אז '''המטריצה אינה לכסינה''' ולא צריך להמשיך. | ||
| − | + | כל עוד יש מספיק וקטורים כמו בריבוי האלגברי, ממשיכים הלאה לערכים העצמיים הבאים. | |
| − | + | ||
| + | *תזכורת למעוניינים: [[88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/7|מציאת בסיס למרחב האפס]] | ||
===בדיקה האם המטריצה לכסינה, ואם כן מציאת המטריצה המלכסנת=== | ===בדיקה האם המטריצה לכסינה, ואם כן מציאת המטריצה המלכסנת=== | ||
| − | אם | + | אם הגענו עד שלב זה, מובטח שהמטריצה לכסינה, והמטריצה המלכסנת <math>P</math> היא המטריצה שעמודותיה הם הוקטורים העצמיים בבסיסים שמצאנו. |
| + | כלומר, המטריצה <math>D:=P^{-1}AP</math> היא מטריצה אלכסונית. | ||
| + | |||
| + | בעמודה <math>i</math> של המטריצה <math>D</math> יופיע הערך העצמי המתאים לוקטור העצמי ששמנו בעמודה <math>i</math> של <math>P</math>. | ||
| + | |||
| − | + | ==דוגמאות== | |
גרסה אחרונה מ־09:32, 21 באוקטובר 2012
תהי נתונה מטריצה  . נרצה לבדוק האם היא לכסינה, ואם כן - למצוא מטריצה שמלכסנת אותה.
. נרצה לבדוק האם היא לכסינה, ואם כן - למצוא מטריצה שמלכסנת אותה.
תוכן עניינים
מציאת פולינום אופייני
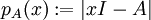 .
.
מציאת הערכים העצמיים של המטריצה וריבויים האלגברי
 ערך עצמי של
ערך עצמי של  אם ורק אם
אם ורק אם 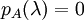 .
.
לכל שורש  של
של 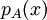 , נוציא מהפולינום גורם
, נוציא מהפולינום גורם  ,
עד שנגיע למצב
,
עד שנגיע למצב
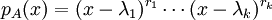 .
.
אם נותר בפולינום גורם שאינו מתפרק לגורמים לינאריים כאלה, אז המטריצה אינה לכסינה ואפשר לעצור כאן.
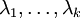 הם הערכים העצמיים השונים של
הם הערכים העצמיים השונים של  ,
ו
,
ו
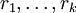 הם הריבויים האלגבריים שלהם, בהתאמה.
הם הריבויים האלגבריים שלהם, בהתאמה.
מציאת בסיסים למרחבים העצמיים
לכל ערך עצמי  של
של  , מחשבים את המרחב העצמי
, מחשבים את המרחב העצמי
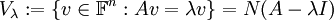 ,
אוסף הפתרונות של המערכת ההומוגנית המתאימה למטריצה
,
אוסף הפתרונות של המערכת ההומוגנית המתאימה למטריצה 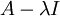 .
.
מוצאים בסיס עבור מרחב זה. אם בבסיס יש פחות איברים מהריבוי האלגברי של  ,
אז המטריצה אינה לכסינה ולא צריך להמשיך.
,
אז המטריצה אינה לכסינה ולא צריך להמשיך.
כל עוד יש מספיק וקטורים כמו בריבוי האלגברי, ממשיכים הלאה לערכים העצמיים הבאים.
- תזכורת למעוניינים: מציאת בסיס למרחב האפס
בדיקה האם המטריצה לכסינה, ואם כן מציאת המטריצה המלכסנת
אם הגענו עד שלב זה, מובטח שהמטריצה לכסינה, והמטריצה המלכסנת  היא המטריצה שעמודותיה הם הוקטורים העצמיים בבסיסים שמצאנו.
כלומר, המטריצה
היא המטריצה שעמודותיה הם הוקטורים העצמיים בבסיסים שמצאנו.
כלומר, המטריצה 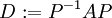 היא מטריצה אלכסונית.
היא מטריצה אלכסונית.
בעמודה 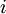 של המטריצה
של המטריצה 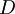 יופיע הערך העצמי המתאים לוקטור העצמי ששמנו בעמודה
יופיע הערך העצמי המתאים לוקטור העצמי ששמנו בעמודה 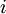 של
של  .
.