הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 8"
(←הלמה של צורן) |
מ (←אקסיומת הבחירה ואקסיומות שקולות) |
||
| (35 גרסאות ביניים של 3 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | '''[[ | + | '''[[מתמטיקה בדידה - מערך תרגול|חזרה למערכי התרגול]]''' |
| − | |||
| − | '''הגדרה.''' קבוצה A אשר מוגדר עליה יחס סדר חלקי R נקראת קבוצה '''סדורה חלקית'''. תת קבוצה של קבוצה סדורה חלקית <math>C\subseteq A</math> נקראת '''שרשרת''' אם R מהווה יחס סדר מלא על C. | + | ====הגדרת שרשרת בקס"ח==== |
| + | '''הגדרה.''' קבוצה A אשר מוגדר עליה יחס סדר חלקי R נקראת קבוצה '''סדורה חלקית'''. תת קבוצה של קבוצה סדורה חלקית <math>C\subseteq A</math> נקראת '''שרשרת''' אם R מהווה יחס סדר מלא/משווה על C. כלומר לכל <math>c_1,c_2\in C</math> מתקיים כי <math>c_1Rc_2</math> או <math>c_2Rc_1</math>. שימו לב כי עבור <math>C=\{\}</math> (הקבוצה הריקה) היא תמיד שרשרת. גם לכל <math>a\in A</math> מתקיים כי עבור <math>C=\{a\}</math> היא תמיד שרשרת. | ||
| − | + | דוגמה פרטית וחשובה: עבור A שהיא קבוצה של קבוצות ו R הוא יחס ההכלה, שרשרת C היא קבוצה של חלק מהקבוצות ב A המקיימות כי כל שתי קבוצות ב C או שהראשונה מוכלת בשניה או שהשניה מוכלת בראשונה. | |
| − | + | =אקסיומת הבחירה ואקסיומות שקולות= | |
| + | '''אקסיומת הבחירה.''' תהי <math>\{A_i\}_i{\in I}</math> משפחה של קבוצות לא ריקות. אזי קיימת פונקציה <math>f:\{A_i\}_{i\in I}\rightarrow\bigcup_{i\in I}A_i </math> המקיימת <math>\forall i\in I:f(A_i)\in A_i</math>. במילים פשוטות: ניתן לבנות פונקציה הבוחרת נציג מכל קבוצה. | ||
| + | תחת אקסיומות ZF (רשימת של אקסיומות "סטנדרטיות", לא משנה אם שמעתם עליהם או לא), הדברים הבאים שקולים לאקסיומת הבחירה: | ||
| − | ''' | + | *'''הלמה של צורן.''': תהי A קבוצה סדורה חלקית '''לא ריקה''' כך שלכל שרשרת המוכלת בA קיים חסם מלעיל מA. אזי קיים בA איבר מקסימלי (איבר שאין איבר שונה ממנו הגדול ממנו). |
| + | *'''עקרון המקסימום של האוסדורף''': כל שרשרת מוכלת בשרשרת מקסימלית (שרשרת מקסימאלית = שרשרת שלא מוכלת ממש באף שרשרת אחרת. לחילופין, כל איבר שנוסיף לשרשרת תגרום לה לא להיות שרשרת) | ||
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | ===דוגמה=== | ||
| + | תהי <math>f:A\rightarrow B</math> פונקציה. הוכח שקיים צמצום חח"ע של f בעל תמונה זהה ל-f. | ||
| + | |||
| + | ==== הוכחה==== | ||
| + | ===== באמצעות אקסיומת הבחירה===== | ||
| + | נציג את A כאיחוד אוסף המקורות של כל התמונות של הפונקציה <math>A=\bigcup_{b\in im(f)}f^{-1}\Big[\{b\}\Big]</math>. לפי אקסיומת הבחירה ניתן לבנות פונקציה | ||
<math>g:\Big\{f^{-1}\Big[\{b\}\Big]:b\in im(f)\Big\}\rightarrow A</math> השולחת כל קבוצת מקורות לנציג כלשהו שלה. | <math>g:\Big\{f^{-1}\Big[\{b\}\Big]:b\in im(f)\Big\}\rightarrow A</math> השולחת כל קבוצת מקורות לנציג כלשהו שלה. | ||
נוכיח כי <math>h:=f|_{im(g)}</math> הינה חח"ע והתמונה שלה שווה לזו של f. נניח <math>h(a)=h(b)</math> לכן <math>a,b\in f^{-1}\Big[\{h(a)\}\Big]</math> אבל כל מקור של תמונה נשלח לנציג '''יחיד''' על ידי g אחרת זו סתירה לחד ערכיות ולכך ש-g הינה פונקציה. כמו כן, מכיוון שמכל מקור נבחר נציג, כל התמונה של f מתקבלת. | נוכיח כי <math>h:=f|_{im(g)}</math> הינה חח"ע והתמונה שלה שווה לזו של f. נניח <math>h(a)=h(b)</math> לכן <math>a,b\in f^{-1}\Big[\{h(a)\}\Big]</math> אבל כל מקור של תמונה נשלח לנציג '''יחיד''' על ידי g אחרת זו סתירה לחד ערכיות ולכך ש-g הינה פונקציה. כמו כן, מכיוון שמכל מקור נבחר נציג, כל התמונה של f מתקבלת. | ||
| + | ===== באמצעות הלמה של צורן===== | ||
| + | נביט באוסף תתי הקבוצות של A כך שהצמצום של f עליהן חח"ע. (האוסף לא ריק כי תמיד אפשר להצטמצם לקבוצה הריקה) | ||
| − | + | ט: תהא <math>\{A'_i\}_{i\in I}</math> שרשרת כלשהיא של קבוצת שהצמצום של f עליהם חח"ע אזי הצמצום של f על <math>\hat{A}:=\bigcup_{i\in I}A'_i</math> ג"כ חח"ע | |
| − | ''' | + | ה: יהיו <math>x\not=y \in \hat{A}</math> אזי קיים <math>j,i\in I</math> כך ש <math>x \in A'_i, y \in A'_j</math>. כיוון שמדובר בשרשרת (היחס מצומצם אליה הוא יחס מלא) אזי |
| + | |||
| + | או ש <math>A'_i \subseteq A'_j</math> או <math>A'_j \subseteq A'_i</math> נניח בה"כ <math>A'_j \subseteq A'_i</math> אזי <math>x\not= y \in A'_i </math> | ||
| + | כיוון שהצמצום של f על <math>A'_i</math> היא חח"ע נקבל כי <math>f(x)\not=f(y)</math> | ||
| + | |||
| + | לפי הלמה של צורן קיים <math>\hat{A}\subseteq A </math> מקסמאלית כך ש f מצומצמת עליה חח"ע. | ||
| + | |||
| + | ט: <math>im(f|_{\hat{A}})=im(f)</math> | ||
| + | |||
| + | ה: אחרת קיים <math>y\in im(f)/ im(f|_{\hat{A}})</math> נבחר מקור <math>x\in A</math> ל <math>y</math> | ||
| + | ואז <math>\hat{A}\cup \{x\}</math> קבוצה שמכילה ממש את <math>\hat{A}</math> והצמצום של f עליה חח"ע. סתירה. | ||
| + | |||
| + | =====באמצעות עקרון המקסימום של האוסדורף===== | ||
| + | נגדיר <math>\mathcal{O}= \{A'\subseteq A\mid f|_{A'} \text{ is 1-1 function }\}</math> להיות קבוצה כל תתי הקבוצות של A שהצמצום של f עליהם היא חח"ע. נסתכל על הקסח <math>\mathcal{O}</math> עם יחס ההכלה. ונסתכל על השרשרת <math>\{\emptyset\}</math> (שימו לב שהצמצום לפונקציה הריקה היא הפונקציה (הקבוצה) הריקה והיא חח"ע). | ||
| + | לפי עקרון המקסימום של האוסדורף קיימת שרשרת מקסמאלית C המכילה את <math>\{\emptyset\}</math>. נגדיר <math>\hat{A} = \cup_{A'\in C}f</math>. | ||
| + | |||
| + | ט: צמצום f על <math>\hat{A}</math> היא חח"ע | ||
| + | |||
| + | ה: נניח <math>x_1\neq x_2\in \hat{A}</math> אזי קיימות <math>A'_1,A'_2\in C</math> כך ש <math>x_i\in A'_i</math>. מכיוון ש C שרשרת נקבל ש <math>A'_1\subseteq A'_2</math> או להיפך. בה"כ <math>A'_1\subseteq A'_2</math> ולכן <math>x_1,x_2\in A'_2</math> ומכיוון שהצמצום של f על <math> A'_2</math> היא חח"ע, נקבל כי <math>x_1,x_2</math> ממופים לתמונת שונות כנדרש. | ||
| + | |||
| + | ט: התמונה של הצמצום של f על <math>\hat{A}</math> היא <math>Im(f)</math>, כלומר <math>Im(f|_{\hat{A}})=Im(f)</math> | ||
| + | |||
| + | ה: נב"ש שקיים <math>b\in Im(f)</math> שאין לו מקור ב <math>\hat{A}</math> אזי, לפי הגדרת התמונה של f, קיים <math>a\in A</math> (כך ש <math>a\notin \hat{A}</math>) המקיים כי <math>f(a)=b</math>. נקבל כי <math>\hat{A}\cup \{a\}</math> מכילה ממש את <math>\hat{A}</math> והצמצום עליה חח"ע (השתכנעו!) ולכן אם נוסיף את <math>\hat{A}\cup \{a\}</math> לשרשרת C נקבל שרשרשת שמכילה ממש את C בסתירה למקסמאליות של C. | ||
| + | |||
| + | ===תרגיל ממבחן תשס"ט מועד א' (ד"ר שי סרוסי וד"ר אלי בגנו)=== | ||
| + | קבוצה נקראת "מגניבה" אם ההפרש בין כל שני איברים שונים בה אינו רציונאלי. | ||
| + | |||
| + | 1. הוכח כי קיימת קבוצה מגניבה C כך שלכל <math>C\subset B</math> מתקיים כי B אינה מגניבה. | ||
| + | |||
| + | 2. כמו כן, הוכח שמתקיים שלכל איבר שאינו ב-C יש איבר מ-C אשר ההפרש בינהם רציונאלי. | ||
| + | |||
| + | ====הוכחה==== | ||
| + | הוכחת 1. שקולה ללהוכיח כי קיימת קבוצה מגניבה C מקסימאלית ביחס להכלה. נוכיח: | ||
| + | |||
| + | ===== לפי הלמה של צורן ===== | ||
| + | נביט באוסף הקבוצות המגניבות וביחס ההכלה (האוסף לא ריק כי כל נקודון הוא קבוצה מגניבה). לכל שרשרת של קבוצות מגניבות מתקיים כי האיחוד הכללי שלהן הינו קבוצה מגניבה. אמנם, אם x,y באיחוד הכללי אזי קיימות קבוצות בשרשרת S,T כך ש <math>x\in S \and y\in T</math>. מכיוון שזו שרשרת, ניתן ללא הגבלת הכלליות לומר כי <math>S\subseteq T</math> ולכן <math>x,y\in T</math> ולכן ההפרש בינהן אינו רציונאלי כפי שרצינו. | ||
אם כן, האיחוד הכללי הינו חסם מקסימלי של השרשרת (כי הוא מכיל את כל הקבוצות בשרשרת) מתוך אוסף הקבוצות המגניבות, ולכן לפי הלמה של צורן קיימת קבוצה מגניבה מקסימלית ביחס להכלה. זה אומר שכל קבוצה מגניבה המכילה את C שווה לה. | אם כן, האיחוד הכללי הינו חסם מקסימלי של השרשרת (כי הוא מכיל את כל הקבוצות בשרשרת) מתוך אוסף הקבוצות המגניבות, ולכן לפי הלמה של צורן קיימת קבוצה מגניבה מקסימלית ביחס להכלה. זה אומר שכל קבוצה מגניבה המכילה את C שווה לה. | ||
| + | ===== לפי עקרון המקסימום של האוסדורף ===== | ||
| + | נגדיר <math>\mathcal{O}</math> אוסף הקבוצות המגניבות, סדורה ע"י הכלה. מתקיים כי <math>\{\emptyset\}</math> שרשרת ולכן היא מוכל בשרשרת מקסימאלית <math>\mathcal{C}</math>. | ||
| + | נגדיר <math>C=\cup_{C'\in \mathcal{C}}</math> | ||
| + | |||
| + | ט: C מגניבה | ||
| + | |||
| + | ה: אם x,y ב C אזי קיימות קבוצות בשרשרת <math>S,T\in \mathcal{C}</math> כך ש <math>x\in S \and y\in T</math>. מכיוון שזו שרשרת, ניתן ללא הגבלת הכלליות לומר כי <math>S\subseteq T</math> ולכן <math>x,y\in T</math> ולכן ההפרש בינהן אינו רציונאלי כפי שרצינו. | ||
| + | |||
| + | ט: C מגניבה ''' מקסימאלית''' (ביחס להכלה) | ||
| + | |||
| + | ה: נב"ש כי קיימת <math>\hat{C}</math> קבוצה מגניבה שמכילה ממש את C אזי <math>\mathcal{C}\cup \{\hat{C}\}</math> היא שרשרת שמכילה ממש את <math>\mathcal{C}</math> בסתירה למקסמאליות של <math>\mathcal{C}</math> | ||
| + | |||
| + | |||
| + | |||
| + | 2. נב"ש שקיים איבר שאין לו הפרש רציונאלי עם אף איבר בC. אזי אם נוסיף אותו לC נקבל קבוצה מגניבה המכילה ממש את C בסתירה. | ||
| + | |||
| + | ===תרגיל=== | ||
| + | הוכח שלכל מרחב וקטורי קיים בסיס (גם אם המרחב אינו מימד סופי) | ||
| + | |||
| + | ====הוכחה==== | ||
| + | יהיה<math> V </math> מרחב וקטורי. ונרצה להוכיח שקיים בסיס למרחב | ||
| + | ===== לפי הלמה של צורן ===== | ||
| + | נביט באוסף הקבוצות הבלתי תלויות שלו | ||
| + | <math>\{B\subseteq V| B \; is \; linearly \; independent \}</math>. (האוסף לא ריק כי קבוצה ריקה היא קבוצה בת"ל) | ||
| + | תהא <math>\{B_i\}_{i\in I}</math> שרשרת של קבוצות בת"ל. | ||
| + | |||
| + | ט: <math>B:=\bigcup_{i\in I}B_i</math> הינו חסם מלעיל של השרשרת (כלומר צ"ל ש <math>B</math> בת"ל | ||
| + | |||
| + | ה: יהיה <math>\alpha_1 v_1 +\cdots +\alpha_n v_n =0</math> צ"ל של וקטורים מ B שמתאפס אזי כל וקטור שייך לאיזה שהוא <math>B_j</math>. כיוון שמדובר בשרשרת אזי כל הוקטורים נמצאים באותה קבוצה. | ||
| + | כלומר <math>\exists k\in I \forall i : v_i \in B_k</math> כיוון ש <math>B_k</math> קבוצה בת"ל נקבל שכל המקדמים שווים לאפס. | ||
| + | |||
| + | לכן יש קבוצה <math>B</math> בת"ל מקסימלית | ||
| + | |||
| + | ט: <math>B</math> פורשת (ולכן מהווה בסיס). | ||
| + | |||
| + | ה: אחרת קיים <math>v\in V\backslash span(B)</math> אבל אז <math>B\cup \{v\} </math> מכילה ממש את B וגם בת"ל. סתירה למקס' של B. | ||
| + | |||
| + | ===== לפי עקרון המקסימום של האוסדורף ===== | ||
| + | נגדיר <math>\mathcal{O}</math> אוסף הקבוצות הבלתי תלויות שמוכלות במרחב. כלומר <math>\{B\subseteq V| B \; is \; linearly \; independent \}</math>. בקס"ח <math>\mathcal{O}</math> סדורה ע"י הכלה מתקיים כי <math>\{\emptyset\}</math> היא שרשרת (קבוצה ריקה היא בת"ל) ולכן היא מוכל בשרשרת מקסימאלית C. נגדיר <math>B=\cup_{B'\in C}B'</math> | ||
| + | |||
| + | ט: <math>B</math> בת"ל | ||
| + | |||
| + | ה: יהיה <math>\alpha_1 v_1 +\cdots +\alpha_n v_n =0</math> צ"ל של וקטורים מ B שמתאפס אזי כל וקטור שייך לאיזה שהוא <math>B_j\in C</math>. כיוון ש C שרשרת אזי כל הוקטורים נמצאים באותה קבוצה. | ||
| + | כלומר <math>\exists k\in I \forall i : v_i \in B_k</math> כיוון ש <math>B_k</math> קבוצה בת"ל נקבל שכל המקדמים שווים לאפס. | ||
| + | |||
| + | ט: <math>B</math> פורשת (ולכן מהווה בסיס). | ||
| + | |||
| + | ה: אחרת קיים <math>v\in V\backslash span(B)</math> אבל אז <math>B\cup \{v\} </math> מכילה ממש את B וגם בת"ל. ולכן אם נוסיף קבוצה זאת ל C נקבל שרשרת שמכילה ממש את C בסתירה למקסימאליות של C. | ||
| + | |||
| + | ===תרגיל=== | ||
| + | תהיינה <math>a<b</math> עוצמות אינסופיות, ותהי קבוצה B כך ש <math>|B|=b</math> | ||
| + | |||
| + | א. הוכח כי קיימת ל-B תת קבוצה A מעוצמה a | ||
| + | |||
| + | ב. הוכח כי B היא איחוד זר של קבוצות אשר כל אחת מהן מעוצמה a. | ||
| + | |||
| + | ====פתרון==== | ||
| + | |||
| + | א. מההגדרה של השוואת עוצמות, קיימת פונקציה חח"ע מקבוצה בעוצמת a אל תוך B. התמונה של פונקציה זו הינה תת קבוצה A בתוך B מעוצמה a. | ||
| + | |||
| + | |||
| + | סעיף ב. נוכיח במספר דרכים: | ||
| + | |||
| + | ===== לפי הלמה של צורן ===== | ||
| + | נביט באוסף כל האוספים של תתי קבוצות זרות של B שכל אחת מהן מעוצמה a. (האוסף לא ריק לפי סעיף קודם) | ||
| + | |||
| + | תהא <math>\{B_i\}_{i\in I}</math> שרשרת של קבוצות כך שכל אחת <math>B_i\in P(P(A)) </math> אוסף של תתי קבוצות זרות של B מעוצמה a. | ||
| + | |||
| + | ט: <math>X:=\bigcup_{i\in I}B_i</math> הינו חסם מלעיל של השרשרת. | ||
| + | |||
| + | ה: לכל 2 תתי קבוצות של B ששיכות ל X קיים <math>i\in I</math> כך ששתי תתי הקבוצות שיכות ל <math>B_i</math> ולכן זרות. | ||
| + | בנוסף כל תת קבוצה של B ששיכת ל X שייכת ל <math>B_i</math> כלשהוא ולכן מעוצמה a. | ||
| + | |||
| + | לפי הלמה של צורן קיים אוסף מקס' S | ||
| + | |||
| + | אם <math>\bigcup S=B</math> אז סיימנו | ||
| + | |||
| + | אחרת <math>D:=B/\bigcup S</math> לא ריקה. אם העוצמה של D גדולה שווה מ a אזי יש לה תת קבוצה מעוצמה a שנוכל לצרף ל S וזה יהיה סתירה למקס' של S. | ||
| + | אם העוצמה שלה קטנה מ a אז נוכל לצרף אותה לאחת מהקבוצות ב<math>S</math> ואז נקבל אוסף של קבוצות מעוצמה a שאיחודם שווה B. | ||
| + | |||
| + | ===== לפי עקרון המקסימום של האוסדורף ===== | ||
| + | נגדיר <math>\mathcal{O}</math> קבוצת כל האוספים של תתי קבוצות זרות של B שכל אחת מהן מעוצמה a. בקס"ח <math>\mathcal{O}</math> עם הכלה מתקיים כי <math>\{\{A\}\}</math> היא שרשרת כאשר A היא תת קבוצה של B מעוצמה a שקיימת לפי סעיף א. כעת לפי עקרון המקסימום, קיימת שרשרת C מקסימאלית. נגדיר <math>T=\cup_{T'\in C}T'</math> | ||
| + | |||
| + | ט: <math>T\in \mathcal{O}</math> | ||
| + | |||
| + | ה: יהיו <math>A_1,A_2\in T</math> אזי קיימות <math>T'_1,T'_2</math> כך ש <math>A_i\in T'_i</math> ומכיוון ש C שרשרת <math>T'_1\subseteq T'_2</math> או להיפך. נניח בה"כ כי <math>T'_1\subseteq T'_2</math> ולכן <math>A_1,A_2\in T'_2</math> ומכיוון ש <math>T'_2\in \mathcal{C}</math> נקבל כי <math>A_1,A_2</math> זרות ומעוצמה a כנדרש | ||
| + | |||
| + | כעת נגדיר <math>B'=\cup_{A'\in T}A'</math> ונגדיר <math>\hat{B}=B\setminus B'</math> . | ||
| + | |||
| + | אם <math>a<|\hat{B}|</math> אז לפי סעיף א' קיימת לה תת קבוצה <math>\hat{A}</math> מעוצמה a. לפי הגדרה <math>\hat{B}</math> מתקיים כי <math>\hat{A}</math> זרה לכל קבוצה ב T ולכן <math>T\cup \{\hat{A}\}\in \mathcal{O}</math> ואם נוסיף אותה ל C נקבל שרשרת שמכילה ממש את C בסתירה למקסימאליות של C. | ||
| + | |||
| + | לכן <math>|\hat{B}|\leq a</math> ונבחר קבוצה אחת A ששייכת T (קיימת לפי סעיף א) ונחליף אותה ב <math>A\cup\hat{B}</math>. מכיוון ש a עוצמה אינסופית נקבל כי <math>A\cup\hat{B}</math> מעוצמה a גם כן (בצירוף <math>|\hat{B}|\leq a</math>) וקיבלנו כעת קבוצות זרות שכל אחת מעוצמה a שהאיחוד של כולם שווה ל B כנדרש | ||
| + | |||
| + | ===תרגיל=== | ||
| + | |||
| + | תהא <math>X</math>. קבוצה <math>F\subseteq P(X)</math> תקרא בוב אם: | ||
| − | + | א. <math>X\in F</math> | |
| − | + | ב. <math>B,C\in F \Rightarrow B\cap C \in F</math> (סגורה לחיתוכים סופיים) | |
| − | + | ג. <math>B \in F \land B\subset C \Rightarrow C\in F</math> (סגורה כלפי מעלה) | |
| − | + | תהא קבוצה <math>A\subseteq P(X)</math> שכל חיתוך סופי של קבוצות בה שונה מקבוצה ריקה. הוכיחו: קיים <math>F\neq P(X)</math> בוב מקסימאלי שמכיל אותה. | |
גרסה אחרונה מ־13:56, 15 באוגוסט 2022
תוכן עניינים
הגדרת שרשרת בקס"ח
הגדרה. קבוצה A אשר מוגדר עליה יחס סדר חלקי R נקראת קבוצה סדורה חלקית. תת קבוצה של קבוצה סדורה חלקית 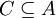 נקראת שרשרת אם R מהווה יחס סדר מלא/משווה על C. כלומר לכל
נקראת שרשרת אם R מהווה יחס סדר מלא/משווה על C. כלומר לכל 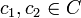 מתקיים כי
מתקיים כי 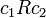 או
או 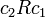 . שימו לב כי עבור
. שימו לב כי עבור 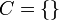 (הקבוצה הריקה) היא תמיד שרשרת. גם לכל
(הקבוצה הריקה) היא תמיד שרשרת. גם לכל  מתקיים כי עבור
מתקיים כי עבור 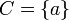 היא תמיד שרשרת.
היא תמיד שרשרת.
דוגמה פרטית וחשובה: עבור A שהיא קבוצה של קבוצות ו R הוא יחס ההכלה, שרשרת C היא קבוצה של חלק מהקבוצות ב A המקיימות כי כל שתי קבוצות ב C או שהראשונה מוכלת בשניה או שהשניה מוכלת בראשונה.
אקסיומת הבחירה ואקסיומות שקולות
אקסיומת הבחירה. תהי 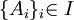 משפחה של קבוצות לא ריקות. אזי קיימת פונקציה
משפחה של קבוצות לא ריקות. אזי קיימת פונקציה 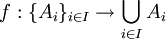 המקיימת
המקיימת 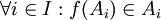 . במילים פשוטות: ניתן לבנות פונקציה הבוחרת נציג מכל קבוצה.
. במילים פשוטות: ניתן לבנות פונקציה הבוחרת נציג מכל קבוצה.
תחת אקסיומות ZF (רשימת של אקסיומות "סטנדרטיות", לא משנה אם שמעתם עליהם או לא), הדברים הבאים שקולים לאקסיומת הבחירה:
- הלמה של צורן.: תהי A קבוצה סדורה חלקית לא ריקה כך שלכל שרשרת המוכלת בA קיים חסם מלעיל מA. אזי קיים בA איבר מקסימלי (איבר שאין איבר שונה ממנו הגדול ממנו).
- עקרון המקסימום של האוסדורף: כל שרשרת מוכלת בשרשרת מקסימלית (שרשרת מקסימאלית = שרשרת שלא מוכלת ממש באף שרשרת אחרת. לחילופין, כל איבר שנוסיף לשרשרת תגרום לה לא להיות שרשרת)
דוגמה
תהי 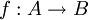 פונקציה. הוכח שקיים צמצום חח"ע של f בעל תמונה זהה ל-f.
פונקציה. הוכח שקיים צמצום חח"ע של f בעל תמונה זהה ל-f.
הוכחה
באמצעות אקסיומת הבחירה
נציג את A כאיחוד אוסף המקורות של כל התמונות של הפונקציה ![A=\bigcup_{b\in im(f)}f^{-1}\Big[\{b\}\Big]](/images/math/f/4/8/f480f427951741ca5efdbf650e6ef7d7.png) . לפי אקסיומת הבחירה ניתן לבנות פונקציה
. לפי אקסיומת הבחירה ניתן לבנות פונקציה
![g:\Big\{f^{-1}\Big[\{b\}\Big]:b\in im(f)\Big\}\rightarrow A](/images/math/8/b/9/8b925537ccc7161837eabd1ae894ada6.png) השולחת כל קבוצת מקורות לנציג כלשהו שלה.
השולחת כל קבוצת מקורות לנציג כלשהו שלה.
נוכיח כי 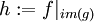 הינה חח"ע והתמונה שלה שווה לזו של f. נניח
הינה חח"ע והתמונה שלה שווה לזו של f. נניח 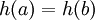 לכן
לכן ![a,b\in f^{-1}\Big[\{h(a)\}\Big]](/images/math/9/9/5/995a59b0d9cd8c832ca25af1973c65a5.png) אבל כל מקור של תמונה נשלח לנציג יחיד על ידי g אחרת זו סתירה לחד ערכיות ולכך ש-g הינה פונקציה. כמו כן, מכיוון שמכל מקור נבחר נציג, כל התמונה של f מתקבלת.
אבל כל מקור של תמונה נשלח לנציג יחיד על ידי g אחרת זו סתירה לחד ערכיות ולכך ש-g הינה פונקציה. כמו כן, מכיוון שמכל מקור נבחר נציג, כל התמונה של f מתקבלת.
באמצעות הלמה של צורן
נביט באוסף תתי הקבוצות של A כך שהצמצום של f עליהן חח"ע. (האוסף לא ריק כי תמיד אפשר להצטמצם לקבוצה הריקה)
ט: תהא 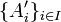 שרשרת כלשהיא של קבוצת שהצמצום של f עליהם חח"ע אזי הצמצום של f על
שרשרת כלשהיא של קבוצת שהצמצום של f עליהם חח"ע אזי הצמצום של f על 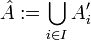 ג"כ חח"ע
ג"כ חח"ע
ה: יהיו 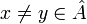 אזי קיים
אזי קיים 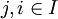 כך ש
כך ש 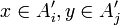 . כיוון שמדובר בשרשרת (היחס מצומצם אליה הוא יחס מלא) אזי
. כיוון שמדובר בשרשרת (היחס מצומצם אליה הוא יחס מלא) אזי
או ש 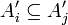 או
או 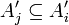 נניח בה"כ
נניח בה"כ 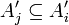 אזי
אזי 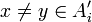 כיוון שהצמצום של f על
כיוון שהצמצום של f על 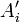 היא חח"ע נקבל כי
היא חח"ע נקבל כי 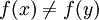
לפי הלמה של צורן קיים 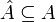 מקסמאלית כך ש f מצומצמת עליה חח"ע.
מקסמאלית כך ש f מצומצמת עליה חח"ע.
ט: 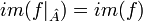
ה: אחרת קיים 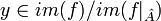 נבחר מקור
נבחר מקור 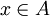 ל
ל 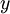 ואז
ואז 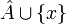 קבוצה שמכילה ממש את
קבוצה שמכילה ממש את 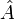 והצמצום של f עליה חח"ע. סתירה.
והצמצום של f עליה חח"ע. סתירה.
באמצעות עקרון המקסימום של האוסדורף
נגדיר 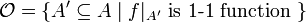 להיות קבוצה כל תתי הקבוצות של A שהצמצום של f עליהם היא חח"ע. נסתכל על הקסח
להיות קבוצה כל תתי הקבוצות של A שהצמצום של f עליהם היא חח"ע. נסתכל על הקסח 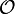 עם יחס ההכלה. ונסתכל על השרשרת
עם יחס ההכלה. ונסתכל על השרשרת 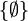 (שימו לב שהצמצום לפונקציה הריקה היא הפונקציה (הקבוצה) הריקה והיא חח"ע).
לפי עקרון המקסימום של האוסדורף קיימת שרשרת מקסמאלית C המכילה את
(שימו לב שהצמצום לפונקציה הריקה היא הפונקציה (הקבוצה) הריקה והיא חח"ע).
לפי עקרון המקסימום של האוסדורף קיימת שרשרת מקסמאלית C המכילה את 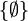 . נגדיר
. נגדיר 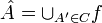 .
.
ט: צמצום f על 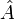 היא חח"ע
היא חח"ע
ה: נניח 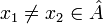 אזי קיימות
אזי קיימות 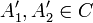 כך ש
כך ש 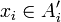 . מכיוון ש C שרשרת נקבל ש
. מכיוון ש C שרשרת נקבל ש 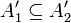 או להיפך. בה"כ
או להיפך. בה"כ 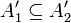 ולכן
ולכן 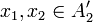 ומכיוון שהצמצום של f על
ומכיוון שהצמצום של f על 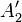 היא חח"ע, נקבל כי
היא חח"ע, נקבל כי 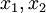 ממופים לתמונת שונות כנדרש.
ממופים לתמונת שונות כנדרש.
ט: התמונה של הצמצום של f על 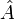 היא
היא 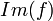 , כלומר
, כלומר 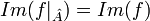
ה: נב"ש שקיים 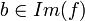 שאין לו מקור ב
שאין לו מקור ב 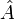 אזי, לפי הגדרת התמונה של f, קיים
אזי, לפי הגדרת התמונה של f, קיים  (כך ש
(כך ש 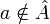 ) המקיים כי
) המקיים כי 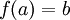 . נקבל כי
. נקבל כי 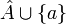 מכילה ממש את
מכילה ממש את 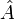 והצמצום עליה חח"ע (השתכנעו!) ולכן אם נוסיף את
והצמצום עליה חח"ע (השתכנעו!) ולכן אם נוסיף את 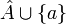 לשרשרת C נקבל שרשרשת שמכילה ממש את C בסתירה למקסמאליות של C.
לשרשרת C נקבל שרשרשת שמכילה ממש את C בסתירה למקסמאליות של C.
תרגיל ממבחן תשס"ט מועד א' (ד"ר שי סרוסי וד"ר אלי בגנו)
קבוצה נקראת "מגניבה" אם ההפרש בין כל שני איברים שונים בה אינו רציונאלי.
1. הוכח כי קיימת קבוצה מגניבה C כך שלכל 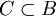 מתקיים כי B אינה מגניבה.
מתקיים כי B אינה מגניבה.
2. כמו כן, הוכח שמתקיים שלכל איבר שאינו ב-C יש איבר מ-C אשר ההפרש בינהם רציונאלי.
הוכחה
הוכחת 1. שקולה ללהוכיח כי קיימת קבוצה מגניבה C מקסימאלית ביחס להכלה. נוכיח:
לפי הלמה של צורן
נביט באוסף הקבוצות המגניבות וביחס ההכלה (האוסף לא ריק כי כל נקודון הוא קבוצה מגניבה). לכל שרשרת של קבוצות מגניבות מתקיים כי האיחוד הכללי שלהן הינו קבוצה מגניבה. אמנם, אם x,y באיחוד הכללי אזי קיימות קבוצות בשרשרת S,T כך ש 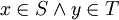 . מכיוון שזו שרשרת, ניתן ללא הגבלת הכלליות לומר כי
. מכיוון שזו שרשרת, ניתן ללא הגבלת הכלליות לומר כי 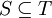 ולכן
ולכן 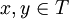 ולכן ההפרש בינהן אינו רציונאלי כפי שרצינו.
ולכן ההפרש בינהן אינו רציונאלי כפי שרצינו.
אם כן, האיחוד הכללי הינו חסם מקסימלי של השרשרת (כי הוא מכיל את כל הקבוצות בשרשרת) מתוך אוסף הקבוצות המגניבות, ולכן לפי הלמה של צורן קיימת קבוצה מגניבה מקסימלית ביחס להכלה. זה אומר שכל קבוצה מגניבה המכילה את C שווה לה.
לפי עקרון המקסימום של האוסדורף
נגדיר 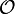 אוסף הקבוצות המגניבות, סדורה ע"י הכלה. מתקיים כי
אוסף הקבוצות המגניבות, סדורה ע"י הכלה. מתקיים כי 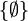 שרשרת ולכן היא מוכל בשרשרת מקסימאלית
שרשרת ולכן היא מוכל בשרשרת מקסימאלית 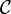 .
נגדיר
.
נגדיר 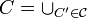
ט: C מגניבה
ה: אם x,y ב C אזי קיימות קבוצות בשרשרת 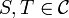 כך ש
כך ש 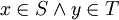 . מכיוון שזו שרשרת, ניתן ללא הגבלת הכלליות לומר כי
. מכיוון שזו שרשרת, ניתן ללא הגבלת הכלליות לומר כי 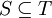 ולכן
ולכן 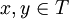 ולכן ההפרש בינהן אינו רציונאלי כפי שרצינו.
ולכן ההפרש בינהן אינו רציונאלי כפי שרצינו.
ט: C מגניבה מקסימאלית (ביחס להכלה)
ה: נב"ש כי קיימת 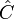 קבוצה מגניבה שמכילה ממש את C אזי
קבוצה מגניבה שמכילה ממש את C אזי 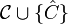 היא שרשרת שמכילה ממש את
היא שרשרת שמכילה ממש את 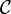 בסתירה למקסמאליות של
בסתירה למקסמאליות של 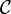
2. נב"ש שקיים איבר שאין לו הפרש רציונאלי עם אף איבר בC. אזי אם נוסיף אותו לC נקבל קבוצה מגניבה המכילה ממש את C בסתירה.
תרגיל
הוכח שלכל מרחב וקטורי קיים בסיס (גם אם המרחב אינו מימד סופי)
הוכחה
יהיה מרחב וקטורי. ונרצה להוכיח שקיים בסיס למרחב
מרחב וקטורי. ונרצה להוכיח שקיים בסיס למרחב
לפי הלמה של צורן
נביט באוסף הקבוצות הבלתי תלויות שלו
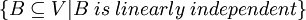 . (האוסף לא ריק כי קבוצה ריקה היא קבוצה בת"ל)
תהא
. (האוסף לא ריק כי קבוצה ריקה היא קבוצה בת"ל)
תהא 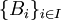 שרשרת של קבוצות בת"ל.
שרשרת של קבוצות בת"ל.
ט: 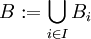 הינו חסם מלעיל של השרשרת (כלומר צ"ל ש
הינו חסם מלעיל של השרשרת (כלומר צ"ל ש  בת"ל
בת"ל
ה: יהיה 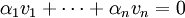 צ"ל של וקטורים מ B שמתאפס אזי כל וקטור שייך לאיזה שהוא
צ"ל של וקטורים מ B שמתאפס אזי כל וקטור שייך לאיזה שהוא 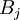 . כיוון שמדובר בשרשרת אזי כל הוקטורים נמצאים באותה קבוצה.
כלומר
. כיוון שמדובר בשרשרת אזי כל הוקטורים נמצאים באותה קבוצה.
כלומר 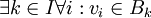 כיוון ש
כיוון ש 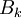 קבוצה בת"ל נקבל שכל המקדמים שווים לאפס.
קבוצה בת"ל נקבל שכל המקדמים שווים לאפס.
לכן יש קבוצה  בת"ל מקסימלית
בת"ל מקסימלית
ט:  פורשת (ולכן מהווה בסיס).
פורשת (ולכן מהווה בסיס).
ה: אחרת קיים 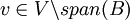 אבל אז
אבל אז 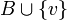 מכילה ממש את B וגם בת"ל. סתירה למקס' של B.
מכילה ממש את B וגם בת"ל. סתירה למקס' של B.
לפי עקרון המקסימום של האוסדורף
נגדיר 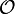 אוסף הקבוצות הבלתי תלויות שמוכלות במרחב. כלומר
אוסף הקבוצות הבלתי תלויות שמוכלות במרחב. כלומר 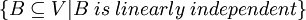 . בקס"ח
. בקס"ח 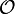 סדורה ע"י הכלה מתקיים כי
סדורה ע"י הכלה מתקיים כי 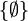 היא שרשרת (קבוצה ריקה היא בת"ל) ולכן היא מוכל בשרשרת מקסימאלית C. נגדיר
היא שרשרת (קבוצה ריקה היא בת"ל) ולכן היא מוכל בשרשרת מקסימאלית C. נגדיר 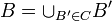
ט:  בת"ל
בת"ל
ה: יהיה 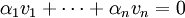 צ"ל של וקטורים מ B שמתאפס אזי כל וקטור שייך לאיזה שהוא
צ"ל של וקטורים מ B שמתאפס אזי כל וקטור שייך לאיזה שהוא 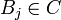 . כיוון ש C שרשרת אזי כל הוקטורים נמצאים באותה קבוצה.
כלומר
. כיוון ש C שרשרת אזי כל הוקטורים נמצאים באותה קבוצה.
כלומר 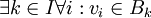 כיוון ש
כיוון ש 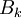 קבוצה בת"ל נקבל שכל המקדמים שווים לאפס.
קבוצה בת"ל נקבל שכל המקדמים שווים לאפס.
ט:  פורשת (ולכן מהווה בסיס).
פורשת (ולכן מהווה בסיס).
ה: אחרת קיים 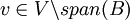 אבל אז
אבל אז 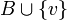 מכילה ממש את B וגם בת"ל. ולכן אם נוסיף קבוצה זאת ל C נקבל שרשרת שמכילה ממש את C בסתירה למקסימאליות של C.
מכילה ממש את B וגם בת"ל. ולכן אם נוסיף קבוצה זאת ל C נקבל שרשרת שמכילה ממש את C בסתירה למקסימאליות של C.
תרגיל
תהיינה 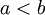 עוצמות אינסופיות, ותהי קבוצה B כך ש
עוצמות אינסופיות, ותהי קבוצה B כך ש 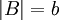
א. הוכח כי קיימת ל-B תת קבוצה A מעוצמה a
ב. הוכח כי B היא איחוד זר של קבוצות אשר כל אחת מהן מעוצמה a.
פתרון
א. מההגדרה של השוואת עוצמות, קיימת פונקציה חח"ע מקבוצה בעוצמת a אל תוך B. התמונה של פונקציה זו הינה תת קבוצה A בתוך B מעוצמה a.
סעיף ב. נוכיח במספר דרכים:
לפי הלמה של צורן
נביט באוסף כל האוספים של תתי קבוצות זרות של B שכל אחת מהן מעוצמה a. (האוסף לא ריק לפי סעיף קודם)
תהא 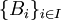 שרשרת של קבוצות כך שכל אחת
שרשרת של קבוצות כך שכל אחת 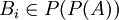 אוסף של תתי קבוצות זרות של B מעוצמה a.
אוסף של תתי קבוצות זרות של B מעוצמה a.
ט: 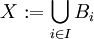 הינו חסם מלעיל של השרשרת.
הינו חסם מלעיל של השרשרת.
ה: לכל 2 תתי קבוצות של B ששיכות ל X קיים 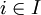 כך ששתי תתי הקבוצות שיכות ל
כך ששתי תתי הקבוצות שיכות ל 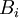 ולכן זרות.
בנוסף כל תת קבוצה של B ששיכת ל X שייכת ל
ולכן זרות.
בנוסף כל תת קבוצה של B ששיכת ל X שייכת ל 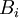 כלשהוא ולכן מעוצמה a.
כלשהוא ולכן מעוצמה a.
לפי הלמה של צורן קיים אוסף מקס' S
אם 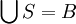 אז סיימנו
אז סיימנו
אחרת 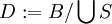 לא ריקה. אם העוצמה של D גדולה שווה מ a אזי יש לה תת קבוצה מעוצמה a שנוכל לצרף ל S וזה יהיה סתירה למקס' של S.
אם העוצמה שלה קטנה מ a אז נוכל לצרף אותה לאחת מהקבוצות ב
לא ריקה. אם העוצמה של D גדולה שווה מ a אזי יש לה תת קבוצה מעוצמה a שנוכל לצרף ל S וזה יהיה סתירה למקס' של S.
אם העוצמה שלה קטנה מ a אז נוכל לצרף אותה לאחת מהקבוצות ב ואז נקבל אוסף של קבוצות מעוצמה a שאיחודם שווה B.
ואז נקבל אוסף של קבוצות מעוצמה a שאיחודם שווה B.
לפי עקרון המקסימום של האוסדורף
נגדיר 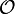 קבוצת כל האוספים של תתי קבוצות זרות של B שכל אחת מהן מעוצמה a. בקס"ח
קבוצת כל האוספים של תתי קבוצות זרות של B שכל אחת מהן מעוצמה a. בקס"ח 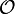 עם הכלה מתקיים כי
עם הכלה מתקיים כי 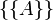 היא שרשרת כאשר A היא תת קבוצה של B מעוצמה a שקיימת לפי סעיף א. כעת לפי עקרון המקסימום, קיימת שרשרת C מקסימאלית. נגדיר
היא שרשרת כאשר A היא תת קבוצה של B מעוצמה a שקיימת לפי סעיף א. כעת לפי עקרון המקסימום, קיימת שרשרת C מקסימאלית. נגדיר 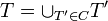
ט: 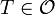
ה: יהיו 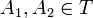 אזי קיימות
אזי קיימות 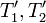 כך ש
כך ש 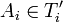 ומכיוון ש C שרשרת
ומכיוון ש C שרשרת 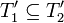 או להיפך. נניח בה"כ כי
או להיפך. נניח בה"כ כי 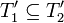 ולכן
ולכן 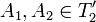 ומכיוון ש
ומכיוון ש 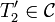 נקבל כי
נקבל כי 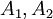 זרות ומעוצמה a כנדרש
זרות ומעוצמה a כנדרש
כעת נגדיר 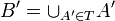 ונגדיר
ונגדיר 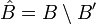 .
.
אם 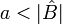 אז לפי סעיף א' קיימת לה תת קבוצה
אז לפי סעיף א' קיימת לה תת קבוצה 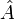 מעוצמה a. לפי הגדרה
מעוצמה a. לפי הגדרה 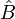 מתקיים כי
מתקיים כי 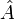 זרה לכל קבוצה ב T ולכן
זרה לכל קבוצה ב T ולכן 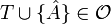 ואם נוסיף אותה ל C נקבל שרשרת שמכילה ממש את C בסתירה למקסימאליות של C.
ואם נוסיף אותה ל C נקבל שרשרת שמכילה ממש את C בסתירה למקסימאליות של C.
לכן 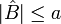 ונבחר קבוצה אחת A ששייכת T (קיימת לפי סעיף א) ונחליף אותה ב
ונבחר קבוצה אחת A ששייכת T (קיימת לפי סעיף א) ונחליף אותה ב 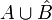 . מכיוון ש a עוצמה אינסופית נקבל כי
. מכיוון ש a עוצמה אינסופית נקבל כי 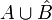 מעוצמה a גם כן (בצירוף
מעוצמה a גם כן (בצירוף 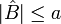 ) וקיבלנו כעת קבוצות זרות שכל אחת מעוצמה a שהאיחוד של כולם שווה ל B כנדרש
) וקיבלנו כעת קבוצות זרות שכל אחת מעוצמה a שהאיחוד של כולם שווה ל B כנדרש
תרגיל
תהא 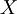 . קבוצה
. קבוצה 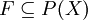 תקרא בוב אם:
תקרא בוב אם:
א. 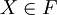
ב. 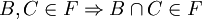 (סגורה לחיתוכים סופיים)
(סגורה לחיתוכים סופיים)
ג. 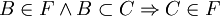 (סגורה כלפי מעלה)
(סגורה כלפי מעלה)
תהא קבוצה 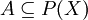 שכל חיתוך סופי של קבוצות בה שונה מקבוצה ריקה. הוכיחו: קיים
שכל חיתוך סופי של קבוצות בה שונה מקבוצה ריקה. הוכיחו: קיים 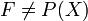 בוב מקסימאלי שמכיל אותה.
בוב מקסימאלי שמכיל אותה.