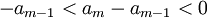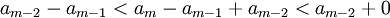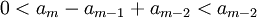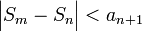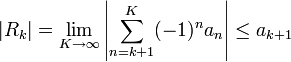הבדלים בין גרסאות בדף "משפט לייבניץ"
מתוך Math-Wiki
מ (משפטים/אינפי/משפט לייבניץ הועבר למשפט לייבניץ) |
Avraham816 (שיחה | תרומות) (←משפט לייבניץ לטורים עם סימנים מתחלפים) |
||
| (6 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | |||
| − | |||
==משפט לייבניץ לטורים עם סימנים מתחלפים== | ==משפט לייבניץ לטורים עם סימנים מתחלפים== | ||
| + | תהי <math>\{a_n\}</math> סדרה חיובית, מונוטונית, השואפת לאפס. אזי: | ||
| − | + | *הטור <math>\displaystyle\sum_{n=1}^\infty(-1)^na_n</math> מתכנס | |
| − | + | *השארית <math>R_k=\displaystyle\sum_{n=1}^\infty(-1)^na_n-\sum_{n=1}^k(-1)^na_n</math> מקיימת <math>|R_k|\le |a_{k+1}|</math> | |
| − | *הטור <math>\sum_{n=1}^\infty (-1)^na_n</math> מתכנס | + | |
| − | *השארית <math>R_k=\sum_{n=1}^\infty (-1)^na_n-\sum_{n=1}^k (-1)^na_n</math> מקיימת <math>|R_k|\ | + | |
===הוכחה=== | ===הוכחה=== | ||
| − | נוכיח כי סדרה הסכומים החלקיים של הטור | + | נוכיח כי סדרה הסכומים החלקיים של הטור הנה סדרת קושי, ועל כן הטור מתכנס. |
| − | יהי | + | יהי <math>\epsilon>0</math>, צריך למצוא מקום בסדרה שהחל ממנו והלאה ההפרש בין כל שני אברים קטן מ- <math>\epsilon</math> . |
| − | *<math>|S_m-S_n|=|(-1)^ma_m+ | + | *<math>\Big|S_m-S_n\Big|=\bigg|(-1)^ma_m+\cdots+(-1)^{n+1}a_{n+1}\bigg|=\bigg|a_m-a_{m-1}+a_{m-2}-\cdots\bigg|</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | נראה כי כל אבר "בולע" את קודמיו, לפי המונוטוניות של הסדרה: | ||
| + | :<math>-a_{m-1}<a_m-a_{m-1}<0</math> | ||
לכן | לכן | ||
| − | + | :<math>a_{m-2}-a_{m-1}<a_m-a_{m-1}+a_{m-2}<a_{m-2}+0</math> | |
| − | + | ||
| − | + | ||
כלומר | כלומר | ||
| − | + | :<math>0<a_m-a_{m-1}+a_{m-2}<a_{m-2}</math> | |
| − | + | ||
| − | + | ||
וכן הלאה עד שנקבל | וכן הלאה עד שנקבל | ||
| + | :<math>\Big|S_m-S_n\Big|<a_{n+1}</math> | ||
| − | + | וכיון ש- <math>a_n</math> שואפת לאפס, החל ממקום מסוים זה קטן מ- <math>\epsilon</math> (ללא תלות ב- <math>m</math>). | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | לפי טיעון דומה, <math>\left|\displaystyle\sum_{n=k+1}^K(-1)^na_n\right|=\bigg|a_{k+1}-a_{k+2}+a_{k+3}-\cdots\bigg|\le a_{k+1}</math> ולכן | ||
| − | + | :<math>|R_k|=\displaystyle\lim_{K\to\infty}\left|\sum\limits_{n=k+1}^K(-1)^na_n\right|\le a_{k+1}</math> | |
| − | + | כפי שרצינו. <math>\blacksquare</math> | |
| − | + | [[קטגוריה:אינפי]] | |
גרסה אחרונה מ־17:51, 9 ביולי 2022
משפט לייבניץ לטורים עם סימנים מתחלפים
תהי 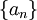 סדרה חיובית, מונוטונית, השואפת לאפס. אזי:
סדרה חיובית, מונוטונית, השואפת לאפס. אזי:
- הטור
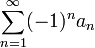 מתכנס
מתכנס - השארית
 מקיימת
מקיימת 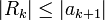
הוכחה
נוכיח כי סדרה הסכומים החלקיים של הטור הנה סדרת קושי, ועל כן הטור מתכנס.
יהי 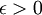 , צריך למצוא מקום בסדרה שהחל ממנו והלאה ההפרש בין כל שני אברים קטן מ-
, צריך למצוא מקום בסדרה שהחל ממנו והלאה ההפרש בין כל שני אברים קטן מ- 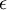 .
.
נראה כי כל אבר "בולע" את קודמיו, לפי המונוטוניות של הסדרה:
לכן
כלומר
וכן הלאה עד שנקבל
וכיון ש-  שואפת לאפס, החל ממקום מסוים זה קטן מ-
שואפת לאפס, החל ממקום מסוים זה קטן מ- 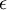 (ללא תלות ב-
(ללא תלות ב- 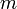 ).
).
לפי טיעון דומה, 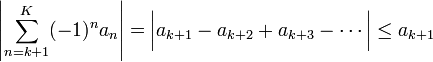 ולכן
ולכן
כפי שרצינו.