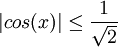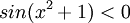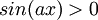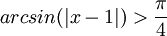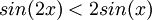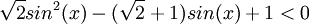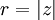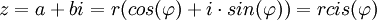הבדלים בין גרסאות בדף "מכינה למחלקת מתמטיקה/מערכי שיעור/4"
מתוך Math-Wiki
(←תרגילים) |
(←מספרים מרוכבים) |
||
| (10 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 12: | שורה 12: | ||
| − | ::<math>arctan(x): | + | ::<math>arctan(x):(-\infty,\infty)\rightarrow [-\frac{\pi}{2},\frac{\pi}{2}]</math> |
'''תרגיל''': הוכח כי <math>sin\Big(arccos(x)\Big)=\sqrt{1-x^2}</math> | '''תרגיל''': הוכח כי <math>sin\Big(arccos(x)\Big)=\sqrt{1-x^2}</math> | ||
| − | |||
==תרגילים== | ==תרגילים== | ||
| שורה 33: | שורה 32: | ||
*<math>arcsin(|x-1|)>\frac{\pi}{4}</math> | *<math>arcsin(|x-1|)>\frac{\pi}{4}</math> | ||
| + | |||
| + | |||
| + | *<math>sin(2x) < 2sin(x)</math> | ||
| + | |||
| + | |||
| + | *<math>\sqrt{2}sin^2(x)-(\sqrt{2}+1)sin(x)+1 < 0</math> | ||
| + | |||
| + | |||
| + | ==מספרים מרוכבים== | ||
| + | |||
| + | ראו את תת הפרק על המספרים המרוכבים, בפרק על שדות מהקורס אלגברה לינארית [[אלגברה לינארית - ארז שיינר#שדה המרוכבים|בקישור הבא]]. | ||
| + | |||
| + | |||
| + | |||
| + | '''תרגיל''' חשבו את <math>z\cdot \overline{z}</math> | ||
| + | |||
| + | '''פתרון''' <math>z\cdot \overline{z} = a^2+b^2</math> | ||
| + | |||
| + | |||
| + | ::הערה: נסמן <math>|z|=\sqrt{a^2+b^2}</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''תרגיל''' הוכיחו שלכל מספר מרוכב <math>z</math> קיים מספר מרוכב <math>z^{-1}</math> כך ש <math>z\cdot z^{-1} = 1</math>. | ||
| + | |||
| + | '''פתרון''': <math>z^{-1}=\frac{\overline{z}}{|z|^2}</math> | ||
| + | |||
| + | |||
| + | ::הערה: באופן כללי נסמן <math>z^{-1}=\frac{1}{z}</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''תרגיל''' חשבו את הביטוי <math>\frac{5+2i}{2-3i}</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''הגדרה''': עבור מספר מרוכב <math>z=a+bi</math> | ||
| + | |||
| + | ::החלק הממשי <math>Re(z)=a</math> | ||
| + | |||
| + | ::החלק המדומה <math>Im(z)=b</math> | ||
| + | |||
| + | |||
| + | לדוגמא: | ||
| + | |||
| + | |||
| + | <math>Im(a-bi) = -b</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''תרגיל''': הוכיחו כי <math>|z|\geq |Re(z)|</math> | ||
| + | |||
| + | |||
| + | '''תרגיל''': הוכיחו את '''אי-שיוויון המשולש''' <math>|z_1+z_2|\leq |z_1|+|z_2|</math> | ||
| + | |||
| + | ==המישור המרוכב== | ||
| + | |||
| + | [[תמונה:complex_plane.png|ימין|400px]] | ||
| + | |||
| + | |||
| + | כל מספר מרוכב <math>a+bi</math> מתאים לנקודה <math>(a,b)</math> במישור המרוכב. | ||
| + | |||
| + | ניתן לתאר את המספר המרוכב באופן יחיד באמצעות המרחק מראשית הצירים וזוית כלפי ציר האיקס. | ||
| + | |||
| + | |||
| + | מתקיים: | ||
| + | |||
| + | |||
| + | ::<math>r=|z|</math> | ||
| + | |||
| + | ::אם <math>a>0</math> אזי <math>\varphi = arctan\Big(\frac{b}{a}\Big)</math> | ||
| + | ::אם <math>a<0</math>אזי <math>\varphi = arctan\Big(\frac{b}{a}\Big)+\pi</math> | ||
| + | ::אם <math>a=0</math> וגם <math>b>0</math> אזי <math>\varphi=\frac{\pi}{2}</math> | ||
| + | ::אם <math>a=0</math> וגם <math>b<0</math> אזי <math>\varphi=-\frac{\pi}{2}</math> | ||
| + | |||
| + | |||
| + | ::<math>z=a+bi=r(cos(\varphi) + i\cdot sin(\varphi)) = rcis(\varphi)</math> | ||
| + | |||
| + | |||
| + | |||
| + | הצורה <math>rcis(\varphi)</math> נקראת ה'''צורה הפולארית''' של המספר המרוכב, ואילו <math>a+bi</math> היא הצורה '''הקרטזית'''. | ||
גרסה אחרונה מ־12:04, 11 באוגוסט 2022
פונקציות טריגונומטריות הופכיות
ניתן להגדיר פונקציה הופכית רק כאשר לכל איבר בתמונה קיים מקור יחיד. לכל פונקציה טריגונומטרית נבחר את התחום המתאים.
תרגיל: הוכח כי 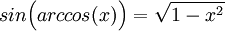
תרגילים
מצא לאילו ערכי x מתקיימים אי השיוויונים הבאים:
מספרים מרוכבים
ראו את תת הפרק על המספרים המרוכבים, בפרק על שדות מהקורס אלגברה לינארית בקישור הבא.
תרגיל חשבו את 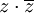
פתרון 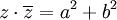
- הערה: נסמן
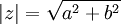
- הערה: נסמן
תרגיל הוכיחו שלכל מספר מרוכב 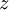 קיים מספר מרוכב
קיים מספר מרוכב 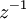 כך ש
כך ש 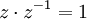 .
.
פתרון: 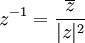
- הערה: באופן כללי נסמן
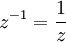
- הערה: באופן כללי נסמן
תרגיל חשבו את הביטוי 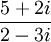
הגדרה: עבור מספר מרוכב 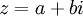
- החלק הממשי
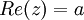
- החלק הממשי
- החלק המדומה
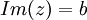
- החלק המדומה
לדוגמא:
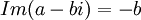
תרגיל: הוכיחו כי 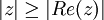
תרגיל: הוכיחו את אי-שיוויון המשולש 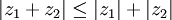
המישור המרוכב
כל מספר מרוכב 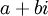 מתאים לנקודה
מתאים לנקודה 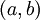 במישור המרוכב.
במישור המרוכב.
ניתן לתאר את המספר המרוכב באופן יחיד באמצעות המרחק מראשית הצירים וזוית כלפי ציר האיקס.
מתקיים:
- אם
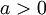 אזי
אזי 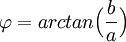
- אם
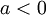 אזי
אזי 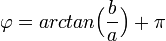
- אם
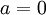 וגם
וגם 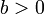 אזי
אזי 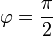
- אם
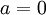 וגם
וגם 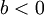 אזי
אזי 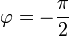
- אם
הצורה 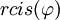 נקראת הצורה הפולארית של המספר המרוכב, ואילו
נקראת הצורה הפולארית של המספר המרוכב, ואילו 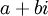 היא הצורה הקרטזית.
היא הצורה הקרטזית.
![arcsin(x):[-1,1]\rightarrow [-\frac{\pi}{2},\frac{\pi}{2}]](/images/math/a/d/8/ad87e9d8d48f94ca443b202a6ac1c6d9.png)
![arccos(x):[-1,1]\rightarrow [0,\pi]](/images/math/4/4/5/445e4a4ac23bf5bc584557717c908d37.png)
![arctan(x):(-\infty,\infty)\rightarrow [-\frac{\pi}{2},\frac{\pi}{2}]](/images/math/d/0/0/d000c19ff4d1baafa10401c931e511b8.png)