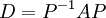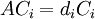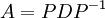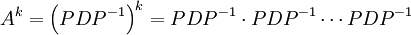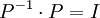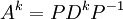הבדלים בין גרסאות בדף "לכסון מטריצה"
(יצירת דף עם התוכן "'''הגדרה:''' תהי A מטריצה ריבועית. אומרים כי A מטריצה '''לכסינה''' אם היא [[דמיון בין מטריצות|דומה...") |
|||
| (2 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 2: | שורה 2: | ||
אומרים כי A מטריצה '''לכסינה''' אם היא [[דמיון בין מטריצות|דומה]] למטריצה אלכסונית | אומרים כי A מטריצה '''לכסינה''' אם היא [[דמיון בין מטריצות|דומה]] למטריצה אלכסונית | ||
| + | |||
| + | |||
| + | '''משפט.''' | ||
| + | |||
| + | תהי <math>A\in\mathbb{F}^{n\times n}</math> מטריצה ריבועית. A לכסינה אם ורק אם קיים בסיס B למרחב <math>\mathbb{F}^n</math> כך שכל הוקטורים בבסיס B הינם וקטורים עצמיים של המטריצה A. | ||
| + | |||
| + | |||
| + | '''הוכחה.''' | ||
| + | |||
| + | ראשית, נניח כי המטריצה A לכסינה. לכן קיימת מטריצה אלכסונית D וקיימת מטריצה הפיכה P כך שמתקיים: | ||
| + | |||
| + | ::<math>D=P^{-1}AP</math> | ||
| + | |||
| + | נכפול משמאל במטריצה P לקבל | ||
| + | |||
| + | ::<math>PD=AP</math> | ||
| + | |||
| + | |||
| + | נסמן את עמודות המטריצה P ב<math>C_1,...,C_n</math> ואת איברי האלכסון של D ב<math>d_1,...,d_n\in\mathbb{F}</math>. | ||
| + | |||
| + | |||
| + | לפי שיטת '''כפל עמודה עמודה''' אנו שמים לב כי השיוויון | ||
| + | |||
| + | ::<math>PD=AP</math> | ||
| + | |||
| + | שקול לכך שלכל i מתקיים | ||
| + | |||
| + | ::<math>AC_i=d_iC_i</math> | ||
| + | |||
| + | ולכן עמודות P מהוות ו"ע של המטריצה A (כמובן ש <math>C_i\neq 0</math> כיוון שP הפיכה). | ||
| + | |||
| + | בנוסף, כיוון שP הפיכה, עמודותיה מהוות בסיס למרחב <math>\mathbb{F}^n</math>. | ||
| + | |||
| + | סה"כ נגיד את B להיות אוסף עמודות P וסיימנו. | ||
| + | |||
| + | |||
| + | |||
| + | בכיוון ההפוך, נניח שיש לנו בסיס כזה B, נשים את איבריו בעמודות מטריצה P. קל לראות כי מתקיים | ||
| + | |||
| + | ::<math>PD=AP</math> | ||
| + | |||
| + | כאשר P הפיכה. לכן נכפול בהופכית לקבל | ||
| + | |||
| + | ::<math>D=P^{-1}AP</math> | ||
| + | |||
| + | כלומר A לכסינה. | ||
| + | |||
| + | |||
==דוגמא חשובה לשימוש בלכסינות== | ==דוגמא חשובה לשימוש בלכסינות== | ||
גרסה אחרונה מ־11:55, 25 באוקטובר 2012
הגדרה: תהי A מטריצה ריבועית.
אומרים כי A מטריצה לכסינה אם היא דומה למטריצה אלכסונית
משפט.
תהי 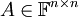 מטריצה ריבועית. A לכסינה אם ורק אם קיים בסיס B למרחב
מטריצה ריבועית. A לכסינה אם ורק אם קיים בסיס B למרחב 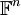 כך שכל הוקטורים בבסיס B הינם וקטורים עצמיים של המטריצה A.
כך שכל הוקטורים בבסיס B הינם וקטורים עצמיים של המטריצה A.
הוכחה.
ראשית, נניח כי המטריצה A לכסינה. לכן קיימת מטריצה אלכסונית D וקיימת מטריצה הפיכה P כך שמתקיים:
נכפול משמאל במטריצה P לקבל
נסמן את עמודות המטריצה P ב ואת איברי האלכסון של D ב
ואת איברי האלכסון של D ב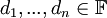 .
.
לפי שיטת כפל עמודה עמודה אנו שמים לב כי השיוויון
שקול לכך שלכל i מתקיים
ולכן עמודות P מהוות ו"ע של המטריצה A (כמובן ש 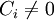 כיוון שP הפיכה).
כיוון שP הפיכה).
בנוסף, כיוון שP הפיכה, עמודותיה מהוות בסיס למרחב 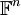 .
.
סה"כ נגיד את B להיות אוסף עמודות P וסיימנו.
בכיוון ההפוך, נניח שיש לנו בסיס כזה B, נשים את איבריו בעמודות מטריצה P. קל לראות כי מתקיים
כאשר P הפיכה. לכן נכפול בהופכית לקבל
כלומר A לכסינה.
דוגמא חשובה לשימוש בלכסינות
באמצעות לכסון ניתן למצוא חזקות גבוהות של מטריצות באופן הבא. נניח A מטריצה לכסינה, לכן קיימת מטריצה אלכסונית D ומטריצה הפיכה P כך שמתקיים:
ולכן
אבל
לכן סה"כ אנחנו מקבלים
כאשר להעלות מטריצה אלכסונית בחזקה זה קל מאד.