הבדלים בין גרסאות בדף "שיחה:89-214 הדרכות והסברים"
(←5.3.9) |
חיים רוזנר (שיחה | תרומות) (תרגיל 9) |
||
| (5 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 4: | שורה 4: | ||
הבהרה לגבי חבורת קיילי (<math>K</math>) - אם תשימו לב, בתרגיל 5.5 יש תרגיל שמבקש להוכיח שזו היא תת-חבורה נורמלית של <math>S_4</math>. אתם רשאים להתשתמש בעובדה זו כמשפט. ייתכן שנוכיח אותה בתרגול או ניתן כתרגיל בית בהמשך. | הבהרה לגבי חבורת קיילי (<math>K</math>) - אם תשימו לב, בתרגיל 5.5 יש תרגיל שמבקש להוכיח שזו היא תת-חבורה נורמלית של <math>S_4</math>. אתם רשאים להתשתמש בעובדה זו כמשפט. ייתכן שנוכיח אותה בתרגול או ניתן כתרגיל בית בהמשך. | ||
| − | '''הבהרה נוספת:''' מכיוון ש <math>A_4\leq S_4 </math> אם תסתכלו על <math>K</math> כעל תת-חבורה של <math>S_4</math> הדוגמה הנגדית שתמצאו תשאר להיות נכונה. לכן, בפועל על מנת לפתור את השאלה הזאת אין צורך לדעת מה זה <math>A_4</math>. | + | '''הבהרה נוספת:''' מכיוון ש <math>A_4\leq S_4 </math>, אם תסתכלו על <math>K</math> כעל תת-חבורה של <math>S_4</math> הדוגמה הנגדית שתמצאו תשאר להיות נכונה. לכן, בפועל על מנת לפתור את השאלה הזאת אין צורך לדעת מה זה <math>A_4</math>. |
== 5.3.13 == | == 5.3.13 == | ||
| שורה 35: | שורה 35: | ||
== 5.4.10 == | == 5.4.10 == | ||
אם אתם מתסבכים אם <math>U_{15}</math>, ניתן לקחת חבורה אחרת. הצעה - קחו <math>\mathbb{Z}_2\times\mathbb{Z}_4</math>. (שהיא איזומורפית ל <math>U_{15}</math> ) | אם אתם מתסבכים אם <math>U_{15}</math>, ניתן לקחת חבורה אחרת. הצעה - קחו <math>\mathbb{Z}_2\times\mathbb{Z}_4</math>. (שהיא איזומורפית ל <math>U_{15}</math> ) | ||
| + | |||
| + | = תרגיל 6 = | ||
| + | שימו לב לכמה נקודות. | ||
| + | |||
| + | 1) <math>\mathbb{Z} / n\mathbb{Z} = \mathbb{Z}_n</math>. שימו לב, בתרגולים הראשונים כך הגדרנו את <math>\mathbb{Z}</math> בלי לציין שזו מנה. | ||
| + | |||
| + | 2) כאשר אתם מקבלים חבורה ולא מציינים את הפעולה - בד"כ מדובר בחבורה שכבר ראיתם, כי רק היא מגדירה חבורה באופן טבעי. למשל, על <math>\mathbb{R}^*</math> אתם לא מכירים שום פעולה חוץ מכפל. | ||
| + | |||
| + | |||
| + | '''שאלה''': האם ניתן להעזר בפונקציית אויילר בשביל לפתור את שאלה 6? | ||
| + | |||
| + | =תרגיל 9= | ||
| + | ==חלק 1 שאלה 3== | ||
| + | הדרכה לתרגיל: עברו על האפשרויות השונות לחבורות אבליות מסדר 62, וחפשו בהן את החבורות המקיימות את התנאים שבשאלה. | ||
גרסה אחרונה מ־13:22, 21 בינואר 2013
תוכן עניינים
תרגיל 5
5.3.9
הבהרה לגבי חבורת קיילי (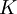 ) - אם תשימו לב, בתרגיל 5.5 יש תרגיל שמבקש להוכיח שזו היא תת-חבורה נורמלית של
) - אם תשימו לב, בתרגיל 5.5 יש תרגיל שמבקש להוכיח שזו היא תת-חבורה נורמלית של 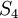 . אתם רשאים להתשתמש בעובדה זו כמשפט. ייתכן שנוכיח אותה בתרגול או ניתן כתרגיל בית בהמשך.
. אתם רשאים להתשתמש בעובדה זו כמשפט. ייתכן שנוכיח אותה בתרגול או ניתן כתרגיל בית בהמשך.
הבהרה נוספת: מכיוון ש 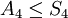 , אם תסתכלו על
, אם תסתכלו על 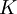 כעל תת-חבורה של
כעל תת-חבורה של 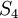 הדוגמה הנגדית שתמצאו תשאר להיות נכונה. לכן, בפועל על מנת לפתור את השאלה הזאת אין צורך לדעת מה זה
הדוגמה הנגדית שתמצאו תשאר להיות נכונה. לכן, בפועל על מנת לפתור את השאלה הזאת אין צורך לדעת מה זה 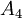 .
.
5.3.13
היכנם מתבקשים להראות מצד אחד שהליבה היא תת-חבורה נורמלית, ומצד שני שהיא מקסימלית ביחס להכלה מבין כל תתי-חבורות הנורמליות של 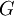 שמוכלות ב
שמוכלות ב 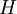 . זאת אומרת, לכל תת-חבורה
. זאת אומרת, לכל תת-חבורה 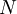 נורמלית של
נורמלית של 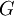 שמוכלת ב
שמוכלת ב 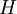 , מתקיים
, מתקיים 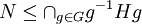
שאלה: אתם יכולים לתת דוגמא לאיך האיברים בליבה ניראים? אם יש לנו נגיד 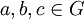 אז זה חיתוך של
קבוצה שנראית ככה:
אז זה חיתוך של
קבוצה שנראית ככה:
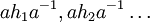 עם קבוצה שנראית ככה:
עם קבוצה שנראית ככה:
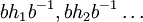 וכו'.
וכו'.
תשובה: איבר היחידה הוא בליבה. מעבר לזה - אין צורך לדעת לצורך פתרון של השאלה. בסה"כ הבנת את ההגדרה נכון.
שאלה קטנה נוספת: אז לא צריך להוכיח שהיא תת חבורה? רק נורמליות ואז להראות מקסימליות?
תשובה לשאלה הקטנה: צריך. שים לב שההוכחה לוקחת בערך שורה.
5.3.11
הכוונה היא לחבורה שנוצרת על ידי הקבוצה 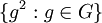 . זאת אומרת אוסך כל המכפלות הסופיות מהצורה
. זאת אומרת אוסך כל המכפלות הסופיות מהצורה 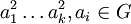 . אין צורך להוכיח זאת בתרגיל, אבל תבדקו עם עצמכם שאתם מבינים מדוע זו חבורה בכלל. עליכם להראות שחבורה זו נורמלית.
. אין צורך להוכיח זאת בתרגיל, אבל תבדקו עם עצמכם שאתם מבינים מדוע זו חבורה בכלל. עליכם להראות שחבורה זו נורמלית.
5.3.14
לשאלת התלמידים ששאלו איך לפתור את סעיף ג' - הרעיון הוא להשתמש בסעיף א. כיצד הראתם נורמליות של
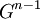 ?
?
שימו לב שמדובר ב-n נתון מראש. בנוסף - יש להראות ש 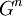 היא תת-חבורה של
היא תת-חבורה של 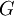 . בסעיף א' ובכל שאר הסעיפים מדובר באותו n שמופיע בנתון.
. בסעיף א' ובכל שאר הסעיפים מדובר באותו n שמופיע בנתון.
5.4.10
אם אתם מתסבכים אם 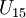 , ניתן לקחת חבורה אחרת. הצעה - קחו
, ניתן לקחת חבורה אחרת. הצעה - קחו 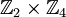 . (שהיא איזומורפית ל
. (שהיא איזומורפית ל 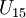 )
)
תרגיל 6
שימו לב לכמה נקודות.
1) 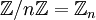 . שימו לב, בתרגולים הראשונים כך הגדרנו את
. שימו לב, בתרגולים הראשונים כך הגדרנו את 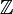 בלי לציין שזו מנה.
בלי לציין שזו מנה.
2) כאשר אתם מקבלים חבורה ולא מציינים את הפעולה - בד"כ מדובר בחבורה שכבר ראיתם, כי רק היא מגדירה חבורה באופן טבעי. למשל, על 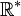 אתם לא מכירים שום פעולה חוץ מכפל.
אתם לא מכירים שום פעולה חוץ מכפל.
שאלה: האם ניתן להעזר בפונקציית אויילר בשביל לפתור את שאלה 6?
תרגיל 9
חלק 1 שאלה 3
הדרכה לתרגיל: עברו על האפשרויות השונות לחבורות אבליות מסדר 62, וחפשו בהן את החבורות המקיימות את התנאים שבשאלה.