הבדלים בין גרסאות בדף "אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏שאלות)
(ביטול גרסה 5876 של 87.68.229.138 (שיחה))
 
(292 גרסאות ביניים של 40 משתמשים אינן מוצגות)
שורה 38: שורה 38:
  
 
'''[[אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות - ארכיון 15| ארכיון 15]]''' - תרגיל 10
 
'''[[אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות - ארכיון 15| ארכיון 15]]''' - תרגיל 10
 +
 +
'''[[אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות - ארכיון 16| ארכיון 16]]''' - לקראת המבחן
 +
 +
'''[[אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות - ארכיון 17| ארכיון 17]]''' - לקראת המבחן
  
 
=שאלות=
 
=שאלות=
  
 
==שאלה==
 
==שאלה==
−
מתי תעלו תרגיל 11 + הפתרון שלו על טורי חזקות? זה ממש חשוב לראות תרגילים עם פתרונות למבחן...
 
−
==שאלה==
 
−
בבוחן, בשאלה 1, היה אפשר גם להוכיח את האי השיוויון הימני עם טיילור עבור x0=0,n=2 לא?
 
  
−
:לא נראה לי... מאיפה אנחנו יודעים איך השארית משפיעה?
+
יהיה במבחן פונקציות עם שתי משתנים?
 +
:לא שידוע לי, אם המרצה אמר שיהיה אז יהיה, אם לא אז לא
 +
 
 +
תומר - מה פתאום שיהיה משהו שלא למדתם ??? הגיון חבר"ה , הגיון !
 +
 
 +
==שאלה==
 +
תחת אילו תנאים ניתן לומר שאינטגרל על סכום אינסופי של פונקציות שווה לסכום האינסופי של האינטגרלים של הפונקציות?
 +
תודה
 +
 
 +
תומר - מפנה אותך לנוסח משפטים המתאימים ! יש משפטים שמתארים תנאים מספיקים לכך . ייתכן שיהיו מצבים נוספים שזה יתקיים אבל אז צריך לבדוק כל מקרה לגופו.
  
 
==שאלה==
 
==שאלה==
−
אם אני רוצה לחשב את סכום הטור : <math>\sum _{n=1}^\infty \frac{1}{2^n n}</math> , אבל כשאני מפרק אותו לאינטגרל לפי רימן (חלוקה של <math>\frac{1}{n}</math> ) אז אני מקבל שזה שווה לאינטגרל: <math>\int _0 ^\infty \frac{1}{2^x}dx</math> וזה יוצא <math>\frac{1}{\ln(2)}</math> , למרות שהסכום לפי מה שבדקתי אמור לצאת <math>\ln(2)</math> . איפה הטעות שלי? אני מניח שהיא איפה שהמרתי סכום לאינטגרל לא אמיתי... איך אפשר לחשב את זה בכל מקרה?
+
נניח יש לי טור פונקציות שרץ על fn (הסדרה המזהה שלו). למה אם הטור |fn| מתכנס במ"ש בI, אז גם הטור המקורי מתכנס במ"ש בI?
 +
 
 +
*נקודתית זה ברור מאינפי 1. לבמ"ש ההוכחה דומה. שארית הטור לא בהחלט קטנה משארית הטור בהחלט, כלומר הטור לא בהחלט מתכנס מהר יותר מאשר הטור בהחלט.
 +
 
 +
ועוד שאלה: אם יש לי סדרת פונ' fn כך ש|fn| מתכנסת לפונ' גבול כלשהי f במ"ש, האם זה אומר שfn המקורית מתכנסת לf1 כלשהי במ"ש?
 +
 
 +
*ברור שלא.... אינפי 1. <math>fn=(-1)^n</math> לא מתכנס בכלל, אבל הערך המוחלט מתכנס במ"ש.
 +
 
 +
יש טעות בסיכום במשפט פרמה, לא? המשפט הראשון בעמוד הראשון של הסיכום...התנאים לא צריעכים להיות הפוכים???
 +
 
 +
*נכון מאד, הסרתי את הסיכום. המשפט אומר שאם יש מקסימום/מינימום והפונקציה גזירה הנגזרת הינה אפס. בוודאי שאם הנגזרת אפס אין שום הכרח שיהיה מינימום/מקסימום (לדוגמא x^3).
 +
 
 +
שאלה:איך מוגדר אינטגרל של פונקציה ממינוס אינסוף לאינסוף? הגבול כאשר c רץ לאינסוף של אינטגרל של הפונקציה מ c- עד c או פשוט פיצול לשני אינטגרלים לא אמיתיים ואז כל אחד שואף בקצב שלו? זה משנה כי במקרה של פונקציה איזוגית-למשל x באפשרות הראשונה זה 0 ובשניה אינסוף פחות אינסוף שזה מתבדר.....(נכון?)תודה.
 +
 
 +
*הוא מוגדר בתור הסכום של שני אינטגרלים לא אמיתיים. האינטגרל על הפונקציה x למשל מתבדר.
 +
 
 +
 
 +
למה אם f פונקציה רציפה, מחזורית ואי-שלילית בממשיים(f אינה זהותית אפס) אז הגבול של f(x)/x^3 אינו אפס כאשר x שואף לאינסוף?? הרי f  חסומה מהנתונים,לא? רוני נתן שאלה כזאת ואמר להוכיח שהאינטרגל של f(x)/x מ1 עד אינסוף מתבדר. ואם הגבול שאמרתי מקודם שווה ל0 אז לפי מבחן ההשוואה האינטגרל מתכנס, אז כנראה שהגבול איננו 0,למה???
  
 
===תשובה===
 
===תשובה===
−
קודם כל אין פה כלל חלוקת רימן (שכן המרחק בין נקודות הדגימה הוא אספוננציאלי עולה, ואילו האורכים הולכים ויורדים לאפס). אפילו אם הייתה, זו חלוקה אינסופית אחת ולא גבול של חלוקות.
 
  
−
פותרים את זה בדיוק כפי שפתרנו אתמול בכיתה. נגדיר <math>S(x)=\sum \frac{1}{n}x^n</math> קל לראות שרדיוס ההתכנסות הוא אחד ולכן זה טור חזקות שמתכנס במ"ש בסביבה של חצי. ברור שסכום הטור שמעניין אותנו הוא <math>S(\frac{1}{2})</math>. מכיוון שההתכנסות היא במ"ש מותר לגזור איבר איבר ולקבל <math>S'(x)=\sum x^{n-1} = \frac{1}{1-x}</math>.  
+
תומר - כמה שאלות , כמה שאלות ! :)
 +
לשאלה הראשונה על התכנסות עם ערך מוחלט גוררת התכנסות בלי , במידה שווה - ראה משפט שהוכחתם . או - אפשר לנסות לבד פשוט ביישום של קריטריון קושי להתכנסות במ"ש ! .
  
−
לכן <math>S(x)=\int_0^x S'(t)dt=-ln(1-x)</math>
+
אינטגרל ממינוס אינס' לאינס' מוגדר על ידי פיצול באיזו נקודת ביניים - אבל בכל אופן כאשר הגבולות שלהם - אחד עם פרמטר לאינסוף ושני עם פרמטר למינוס אינסוף - הם לא תלויים אחד בשני ! ובטח לא ממינוס סי לסי כאשר סי שואף לאינסוף . זהו אינטגרל שקיים בשימושים אבל יש לו שם - PRINCIPAL VALUE - אבל זה לא האינטגרל בקורס שלנו !!! .
  
−
ולכן <math>S(\frac{1}{2})=-ln(\frac{1}{2})=ln2</math>
+
לגבי שאלה אחרונה - תן בבקשה את ניסוח השאלה המלא כדי שאוכל להתייחס .
  
 +
==שאלה מסודרת ==
 +
נתונה פונקציה fרציפה,מחזורית ואי-שלילית ב-R. היא אינה זהותית 0.הוכח: האינטגרל של f(x)/x מ-1 לאינסוף מתבדר. תוכל גם להגיד לי למה אי אפשר להוכיח שזה מתכנס עם שימוש במבחן ההשוואה השני? כי f לפי הנתונים חסומה,לא? ואז הגבול של (f(x)/x)/x^2 שווה לאפס ולפי המבחן f(x)/x מתכנס, כי האינטגרל של x^2 מתכנס...
  
−
עד כדי טעות...
+
===תשובה===
 +
(לא ארז/תומר) נראה לי שהטעות שלך היא כזו , כשאתה עשית את מבחן ההשוואה, עשית את זה עם הפונ' x^2 והאינטרל של זה מתבדר בקטע 1 עד אינסוף (אתה מתבלבל עם 1/x^2).
  
−
הערה: זה תרגיל נחמד שנותן לנו נוסחא לחישוב lnx עם דיוק אספוננטציאלי עבור x>1 (עבור x<1 ניקח את <math>-ln(\frac{1}{x})</math>).  
+
:אבל אמרתי בקטע 1 עד אינסוף...לא מאפס!
−
הנוסחא <math>ln(x)=-ln(\frac{1}{x})=-ln(1-\frac{x-1}{x})=S(\frac{x-1}{x})=\sum_{n=1}^{\infty}\frac{1}{n}(\frac{x-1}{x})^n</math>
+
::הוא העיר לך על הפונקציה ולא על הקטע. x^2 זו פונקציה ששואפת לאינסוף ובפרט אינה אינטגרבילית על הקטע האינסופי.
  
−
נחמד מאוד, הבנתי! על הטריק עם ה-ln שכתבת בהערה אני לא חושב שהייתי מצליח לעלות, אבל אני אזכור אותו עכשיו, תודה רבה!!
+
ובנוגע להוכחה , אני עשיתי את זה בדרך הבאה:
  
−
==שאלה==
+
נסמן את המחזור של F כ-T, אנחנו יודעים שהפונ' אינה זהותית אפס, לכן יש נקודה X0 בקטע [1,1+T] כך ש- (''f''(''x0'' שווה ל-M גדול ממש מאפס. מכיוון ש-F רציפה יש סביבה [a,b] של X0 כך שכל ס בקטע מקיים f(x)>M/2 (או אפילו גדול שווה, זה לא משנה) וכעת, מכיוון ש-F אישלילית , נגדיר פונקציה חדשה G להיות M/2x בכל קטע מהצורה [a+n*T,b+n*T] כאשר n טבעי ואפס בכל נקודה אחרת.
−
יהי <math>\sum _{n=1}^\infty a_n</math> טור חיובי מתכנס, ו- <math>f_n (x)</math> סדרת פונקציות, כך שלכל n טבעי מתקיים: <math>|f_{n+1}(x)-f_n(x)|<a_n</math> . הוכח או הפרך : <math>f_n</math> מתכנסת במידה שווה.
+
  
−
אני מתקשה להבין את הבעייה של ההתכנסות במ"ש במקרה הזה... אז אחרי שלא הצלחתי להפריך, ניסיתי להוכיח, וראיתי שזה קרוב יותר לקריטריון של קושי להתכנסות במ"ש, אז מספיק להראות שאם לכל k יש n טבעי שעבורו <math>|f_{n+1}(x)-f_n(x)|<k</math>, אז גם נובע שלכל m>n מתקיים התנאי של קושי, אבל זה בדיוק מה שאני לא מצליח להראות... איך אני יכול להפריך ע"י מציאת סדרת פונקציות שהפרש של כל פונקציות קרובות שואף לאפס, אבל כשה-n גדל הפונקציות החדשות שנוצרות רחוקות יותר עד כדי חוסר התכנסות במידה שווה או אפילו חוסר התכנסות?
+
ברור כי שתי הפונ' אי שליליות, אינטגרביליות בכל קטע מהצורה [one,R] כש- R>1 (F רציפה בכל קטע כזה, ול-G יש מספר סופי של נקודות אי רציפות מהסוג המתאים) ולכן אם האינטגרל של G בטע 1 עד אינסוף מתבדר, כך גם האינטגרל הלא אמיתי של F.
 +
 
 +
ועכשיו, להראות שהאינטגרל של G בקטע 1 עד אינסוף מתבדר, זה לא כזה מסובך (אני עשיתי לפי קריטריון קושי, אבל אני בטוחשאפשר בעוד דרכים, ואין לי כח לכתוב את זה) ובסה"כ קיבלנו שהאינטגרל של f(x)/x
 +
 
 +
==שאלה==
 +
למה במבחן ההשוואה הראשון רוני ציין שאם 0<g  ו f>g והאינטגרל של f מתכנס(לא אמיתי, בשנ הסוגים הוא אמר ככה...) אז האינטגרל של g מתכנס. הוא לא אמר שאם g מתבדר גם f מתבדר,זה לא נכון??
  
 
===תשובה===
 
===תשובה===
−
זה תרגיל מאינפי 1 בתכלס.
+
המשפט השני הוא היקש לוגי מהראשון. לא יכול להיות שf יתכנס אבל g יתבדר, לכן אם g מתבדר אזי f מתבדר.
−
<math>|f_m-f_n|=|f_m-f_{m-1}+f_{m-1}-....+f_{n+1}-f_n|\leq a_m+...+a_n</math>
+
  
−
אבל לפי תנאי קושי להתכנסות טורים הצד הימני קטן מאפסילון.
+
==שאלה==
−
:אהההה, הבנתי, וזה מתקיים עבור n,m גדולים מספיק (כלומר שגדולים מ-n0 התחלתי)... יפה! הייתי צריך לנסות לקשר את זה לסכום הטור... תודה רבה :) !!!
+
  
 +
בתרגיל 11 שאלה 3 - לעוד מישהו יצא רדיוס התכנסות אפס?
 +
:: [לא תומר או ארז] לי דווקא יצא 1
 
==שאלה==
 
==שאלה==
−
אני מוכרח להבין, מה בעצם המשמעות של "התכנסות במידה שווה" של סדרת פונקציות? ז"א, מה המשמעות הגרפית של זה, בלי שימוש באפסילון וכ'ו? מה בעצם ה"מידה שווה" כאן?
+
אם אני צריכה להוכיח שפונק' כלשהי היא אינטגברילית רימן, והראיתי שהסכום רימן שלה לכל חלוקה מתאימה ולכל בחירה אלפא חסומה בין הסכום רימן של פונק' אינטגרבילית(!) אחרת פחות אפסילון, ואותו סכום ועוד אפסילון. האם זה מראה לי שהפונק' שלי אינטגרבילית גם? ויותר מזאת, שואפת לסכום I של אותה הפונקציה השניה?
 +
:הסכום רימן של הפונקציה האחרת עבור אותה חלוקה? ומה זה האפסילון הזה? במה הוא תלוי?
 +
 
 +
==שאלה==
 +
נתון כי f אינטגרבילית וחסומה ע"י  M. צ"ל שf^2  אינטגרבילית באותו קטע.
 +
יש דרך להראות את זה לא ע"י הרכבת פונקציות (שבדרך זו הנתון ע"י החסימות מיותר)?
 +
מהי הדרך?
 +
 
 +
:הנתון על חסימות מיותר איך שלא תסתכל על זה, שכן זו פונקציה אינטגרבילית (ולכן חסומה)
 +
 
 +
אבל יש דרך להראות את זה חוץ מהרכבה של פונקציה רציפה ופונקציה אינטגרבילית?
 +
 
 +
תומר - מידת קבוצת נקודות אי הרציפות  של הפונקציה החדשה היא אפס ? ...
 +
 
 +
(לא ארז/תומר) כן יש פיתרון אחר, והוא בעזרת תנאי רימן לאינטגרביליות.
 +
f^2 חסומה (ברור), ונותר להראות את התנאי השני.
 +
בקשר אליו, קל להראות ש
 +
 
 +
w(f^2)<= w(f)*2*M (כאשר w הוא התנודה בקטע), ומכאן  קל להמשיך.
 +
 
 +
מראים את זה כך, לכל x1,x2 בקטע כלשהו מתקיים:
 +
f(x1)^2-f(x2)^2<=(f(x1)-f(x2))*(f(x1)+f(x2)), ומכאן זה ברור
 +
 
 +
==שאלה==
 +
התבקשתי להביא דוגמה לסדרת פונק' fn רציפות ב[0,1] כך שfn(x)-->0 לכל X בתחום, אך האינטגרל של fn מ0 עד 1 אינו שווה ל0. 
 +
- האם הפונקציה x^n(x^n-1)  qq  מקיימת את הדרוש? הפונק' אכן רציפות ב[0,1], פונקצית הגבול היא 0, אבל האינטגרל יוצא, אם אני לא טועה, 1/n פחות 1/(2n+1)..
  
 
===תשובה===
 
===תשובה===
−
המשמעות היא שבכל נקודה בפונקציה ההתכנסות היא באותה מהירות פחות או יותר. גרפית, אתה מעתיק את פונקצית הגבול אפסילון למעלה ואפסילון למטה, ואז החלק מn_0 מסויים כל הפונקציות בסדרה מצויירות בגרף בין שתי ההזזות של פונקצית הגבול.
+
אתה בטוח שהאינטגרל שונה מאפס ולא '''שואף''' לאפס? כי כמעט כל סדרה שתבחר תעמוד בתנאי הראשון (למשל הסדרה של הפונקציות הקבועות <math>\frac{1}{n}</math>).
 +
 
 +
אם אתה רוצה סדרה שהאינטגרל עליה אינו שואף לאפס, קח סדרה של פונקציות הבאה: הגרף של הפונקציה ה-n הוא משולש עם בסיס <math>\frac{1}{n}</math> בגובה 2n וכל שאר הפונקציה היא אפס. הסדרה הזו שואפת לאפס (כמובן שלא במ"ש) והאינטגרל על כל פונקציה בסדרה הוא תמיד 1.
 +
 
 +
==שאלה==
 +
נראית נחמדה. f:[0,1] ---> R היא פונקציה רציפה אי שלילית המקיימת f(x)<=sinx לכל x בתחום. צריך למצוא את כל פתרונות המשוואה:
 +
cosx+quad(f,0,x)-1=0.
 +
(קוסינוסX ועוד האינטגרל של f מ0 עד x פחות 1 = 0.)
 +
מעבר לעובדה שx=0 הוא פתרון אחד של המשוואה, לא הצלחתי להוכיח שלא קיימים עוד פתרונות/למצוא פתרון נוסף. ניסיתי להניח שקיים ולהשתמש במשפט רול, ניסיתי להשתמש בזה שאי שיוויון ברמת הפונק' ==> אי שיוויון ברמת האינטגרל אבל בסופו של דבר לא הגעתי למשהו שמוכיח. יש רעיון למישהו?
 +
::מישהו??
 +
 
 +
 
 +
:::אם f=sinx אזי זו הפונקציה הקבועה אפס. אם f קטן ממש מהסינוס אזי הנגזרת בעלת סימן קבוע (שלילי) והפתרון היחיד הוא אפס
 +
 
 +
==שאלה==
 +
מישהו מוכן להסביר לי באילו מקרים כדאי לעשות גזירה איבר איבר, ומתי לעשות אינטגרציה איבר איבר? תודה.
 +
:כדאי? תמיד. מותר? כאשר יש התכנסות במ"ש לפי המשפטים שלמדתם בכיתה.
 +
 
 +
==שאלות מעניינות==
 +
* הוכח או הפרך:
 +
תהי <math>f_n(x)</math> סדרה של פונקציות גזירות ברציפות המתכנסות במ"ש לפוקציה <math>f</math>, אשר גם גזירה ברציפות,ב-<math>[a,b]</math>.
 +
אזי ש- <math>f_n' \rightarrow f'</math> במ"ש על הקטע <math>[a,b]</math>.
 +
* בנוגע למשפט דיני לטורים, נניח שיש לי טור <math>u(x)=\sum_{n=1}^{\infty}a_n(x)</math>, כך ש-<math>a_n(x)>0</math> והטור מתכנס ב-I.
 +
מתי אני יודע אם הפונקציה הגבולית רציפה, כך שאוכל להישתמש בדיני ולקבוע שההתכנסות במ"ש.
 +
נשמח לתשובה ממישהו,די דחוף! תודה!!! :)
 +
 
 +
תומר - אם ניקח את הסידרה cosnx ונחלק הכל ב n . האם קיבלת סידרה שמתכנסת במ"ש ? ומה עם נגזרותיה ? ...
 +
לגבי דיני - פשוט לבדוק רציפות לפי הגדרה - גם לא אמרת שהפונקציות בסידרה רציפות - שים לב לתנאי המשפט ! .
 +
 
 +
==שאלה==
 +
 
 +
שאלה שנתקעתי עליה ואשמח לכיוון:
 +
 
 +
int(arctan(x)/[(x*(ln(x+1))^2)], x = 0 .. infinity)
 +
 
 +
ניסיתי דיריכלה, חשבתי על השוואה, ופשוט לא מצאתי. אשמח לעזרה
 +
 
 +
::מצטרף לשאלה!! איך פותרים את הדבר הזה?
 +
 
 +
 
 +
(לא ארז/תומר) תנסה השוואה עם אחד חלקי [x*ln(x)^2]. שים לב ש arctanx שואף באינסוף לחצי פאי, ושעם קצת אלגברה אפשר להוכיח שמנת ה-ln-ים שואפת לאחד. כדי להראות התכנסות של האינטגרל החדש, אפשר להשתמש בהצבה t=ln(x), או לחילופין להשתמש במבחן האינטגרל+מבחן העיבוי לטורים
 +
 
 +
תודה רבה :)
 +
 
 +
זה לא נכון, כי יש בעיתיות גם בנקודה x=1 וגם באינסוף. ההשואה שנתת עוזרת רק לחלק של האינסוף
 +
 
 +
: אבל אני לא חושב שאמורה להיות בעיה, כי זאת בעיה בנקודה, וזה לא אינטגרל לא אמיתי מסוג שני.
 +
 
 +
::אתה מפצל את זה לשני אינטגרלים: האינטגרל מ-1 עד אינסוף מתכנס (כי מורידים את ה-ln בעזרת אי שוויון והאינטרגל (arctanx/x^2) מתכנס (השוואה עם 1/x^2)...
 +
::עכשיו בקשר לאינטגרל מ-0 עד 1 אתה יודע ש- ln(1+x)<x לכל x ב-[0,1] ולכן האינטרגל שלנו גדול מהאינטגרל של arctan(x)/x^4 וזה מתבדר ע"פ השוואה עם 1/x^4 שמתבדר בקטע [0,1], ולכן זה גדול מאינטגרל מתבדר וזה סה"כ מתבדר. (אשמח לקבל אישור מאחד המתרגלים =) ).
 +
 
 +
:(לא ארז/תומר) עבור האינטגרל מ-0 עד 1, תנסה מבחן השוואה גבולי עם אחד חלקי x^2 . שים לב ש arctanx/x שואף לאחד וש ln(1+x)/x גם שואף לאחד כאשר x שואף לאפס.
 +
ובקשר לזה שכתב מעלי- ה-x במכנה הוא לא בריבוע...
 +
 
 +
:: האמת שהאינטגרל המקורי היה בין 1 לאין סוף וזאת טעות שלי שכתבתי אפס, אבל זה באמת יהיה טוב לדעת מה קורה גם אם זה היה אפס.
 +
:: תודה לשניכם :)
  
−
במילים אחרות, הפונקציות נמצאות במרחק 'קבוע' מפונקצית הגבול ללא תלות באיקס. למה זה עוזר? למשל רציפות. תהי סדרת פונקציות רציפות. ניקח פונקציה f_n מהסדרה עבור n מספיק גדול, ונקח סביבה קטנה של x_0 כלשהו. מתוך רציפות, f_n שולחת את סביבה של x_0 קרוב מאד לf(x_0). אבל, f_n שולחת כל נקודה בסביבה לגובה קרוב מאד לפונקצית הגבול באותה נקודה כאשר המרחק לא תלוי בבחירת הנקודה. לכן גם כל הסביבה של פונקצית הגבול קרובה מאד לf(x_0( ויוצא שגם פונקצית הגבול רציפה.
+
==שאלות.==
 +
*arctanx  חיובי בקטע 1,infinity לא? היה תרגיל באחד המבחנים ששמו ערך מוחלט מסביב לarctan, באנטגרל שהתחום שלו הוא תהחום המצוין..
 +
*במבחן ההשוואה הגבולי. מותר לי להשוות פונק' חיובית עם פונק' שלילית, אם הגבול יוצא חיובי? לדוגמה, הפונקציה sinx חלקי x*lnx. בתחום [0.5,1], נניח ואני רוצה להשוות עם sinx חלקי x-1..
 +
*כאשר אני מפצלת אינטגרלים ל2 תחומים שונים [עם דגש על השונים!]. אם אחד מהם מתבדר, כל האינטגרל המקורי מתבדר, נכון? בלי קשר לחיוביות/שליליות של אחת הפונקציות..
 +
*בהמשך לשאלה שלמעלה - אם יש לי שאלה של 'לאילו ערכי אלפא', כאשר יש לי חיבור של 2 אינטגרלים - אחד ל"א מסוג ראשון והשני ל"א מסוג שני.. אז אם למשל עבור alpha>1 האינטגרל מסוג 1 מתבדר, אין מה לבדוק את האינטגרל השני גם?
  
−
==שאלות==
+
וזהו, תודה רבה!
−
קודם כל, בקשר לאינטגרביליות. לפי הגדרת רימן, מותר לדלתא להיות תלויה במס' הקטעים - n?
+
−
*עוד שאלה. באחד המשפטים בכיתה, רוני כתב משהו כמו "g אינטגרבילית ולכן לכל אפסילון>0 קיימת דלתא, כך שלכל חלוקה T המקיימת שפרמטר החלוקה שלה קטן מדלתא, יתקיים: s(t) עליון פחות s(t) תחתון קטן מאפסילון (סליחה על הכתיבה המסורבלת..)
+
−
זה לא אמור להיות, שלכל אפסילון קיימת חלוקה 'אחת' T שמקיימת את זה? זה לא עירבוב של 2 הגדרות?
+
−
תודה רבה (:
+
  
 
===תשובה===
 
===תשובה===
−
מה זאת אומרת מותר לדלתא? יש פרמטר חלוקה - אורך הקטע הגדול ביותר. הסכומים מתכנסים אם על כל החלוקות החל מפרמטר חלוקה מספיק קטן (דלתא) הסכום קרוב לגבול עד כדי אפסילון. אין פה שום קשר למספר הקטעים בחלוקה. דלתא תלוי בלבד באפסילון, בפונקציה ובקטע.
+
*כן הוא חיובי.
 +
*אם בתחום הפונקציה אי חיובית אז אם תכפלי אותה במינוס תקבל פונקציה אי שלילית. כמובן שמכפלה במינוס לא משנה התכנסות אינטגרל
 +
*נכון.
 +
*נכון
  
−
קודם כל תבדיל בין הגדרה לבין משפט. הגדרה להתכנסות יש רק אחת. כל שאר התנאים להתכנסות שקולים.
+
::כן, אבל כשהפונק' הייתה שלילית, הגבול יצא לי חיובי. אם אני כופלת במינוס 1, הגבול יוצא שלילי..
 +
:::לא יכול להיות שהגבול של המנה של שתי פונקציות אי שליליות יהיה שלילי
 +
::::::: כעיקרון אני מדברת על הפונקציה sinx חלקי x*lnx. בתחום [0.5,1] אני משווה אותה עם sinx חלקי (1 פחות X). (יום יבוא ואני אלמד להשתמש בכתיב המתמטי של ויקיפדיה... מצטערת על הסרבול). בכל מקרה, שתי הפונקציות חיוביות בתחום הזה. אבל הגבול של המנה, כאשר X שואף ל1 מצד שמאל, הוא מינוס אחת..
  
−
בוודאי שאין חלוקה יחידה כזו, הרי כל עידון של החלוקה יקיים את התנאי גם כן. יכול להיות שבהוכחה שלו הוא יכל לרשום פחות דברים, אבל אין ספק שזה מוכיח.
+
:כי ln שלילית בקטע הזה.
−
::::זה נכון שעידון של החלוקה יקיים את התנאי, אבל הוא טען שכל T שיקיים שפרמטר החלוקה שלו יהיה קטן מדלתא, יקיים את החלוקה. למה זה נכון? אני מסכים שלעידון זה יהיה נכון, אבל לא בהכרח לכל T כנ"ל.
+
::אוקי, אז בעצם מכפילים את הפונק' המקורית ב1- ואז מקבלים גבול חיובי, ואומרים שבגלל שהפונק' עם המינוס מתכנסת/מתבדרת ==> כך גם הפונק' המקורית?
  
−
:::::אני מניח שאחר כך הוא הוכיח שבמקרה המסויים זה מתקיים. כמו שאמרתי, יכול להיות שהוא הוכיח יותר ממה שצריך, אבל אם הוא הוכיח, מה רע? שנית, עבור פרמטר חלוקה מספיק קטן המרחק בין הסכום העליון לגבול והמרחק בין הסכום התחתון לגבול הם אפסילון חלקי שתים. לכן המרחק ביניהם הוא אפסילון.
+
:נכון
−
::::::בקשר למשפט הראשון - הוא לא ניסה להוכיח כלום בהתחלה. הוא פשוט הסיק מהנתון, שאם G אינטגרלית אז בוודאי מתקיים מה שכתבתי למעלה..
+
−
::::::: אוקיי.  כמו שהסברתי, זה נכון.
+
  
 
==שאלה==
 
==שאלה==
−
בתרגיל 3 פה: http://www.math.tau.ac.il/~boazslom/hedva2/Exercises/ex-02.pdf
+
התכנסות במ"ש של ערך מוחלט של טור הפונק' גוררת התכנסות במ"ש של טור הפונק'?
−
בפתרונות הם טוענים שמכיוון שf גזירה, ניתן להציב x=f(t). לא ממש הבנתי את הקשר, מישהו יכול להסביר?
+
:כבר נשאל בעמוד זה. כן מכיוון שהשארית של טור קטנה או שווה לשארית של הטור בהחלט
  
 +
==שאלה==
 +
*הסתבכתי,אפשר עזרה?
 +
*נניח שהפונקציה f  מוגדרת ורציפה בקטע סגור x=a..b הוכח כי הסכום מאחד עד אינסוף של f^n מתכנס במ"ש בקטע זה אם ורק אם הסכום הנל(f^n) מתכנס נקודתית בקטע זה.
 +
 +
 +
:השאלה לא מנוסחת טוב. מה זה f ומה הוא קשור? מה ההבדל בין סכום מאחד עד אינסוף לבין טור?
 +
תיקנתי... מה הבעייה בהגדרה של f פשוט פונקציה f(x)
 +
 +
::שאלתי מה הקשר של f. גם g היא פונקציה אבל היא קשורה לשאלה בדיוק כמו f... האם היא פונקצית הגבול של הטור? האם הפונקציות בסדרה רציפות?
 +
 +
: (לא ארז וגם לא תומר) בעצם הכיוון המעניין היחיד הוא מהתכנסות נקודתית לבמ"ש. אם f^n מתכנס נקודתית אפשר לראות כי לכל x נקבל f(x<1 (בערך מוחלט, הלוואי שזה לא היה קופץ כל הזמן). f רציפה לכן הערכים שהיא מקבלת מהווים קטע סגורc,d  בתוך [-1,1), קטע בו הטור x^n מתכנס במ"ש. לכן כל סדרת נקודות אינסופית שתבחר בa,b עבור הטור לפי f שקולה בעצם לבחירת נקודות בc,d עבור הטור של x המתכנס שם במ"ש (ולפי מבחן הLIMSUP בעצם זה כל מה שצריך).
 +
 +
 +
 +
אבל למה f(x) בערך מוחלט קטן מ-1?
 +
:הסברתי במפורט בתשובה. לא בהכרח f<1 פשוט אם הוא מתכנס הוא קטן מאחד ולכן מתכנס במ"ש. אם הוא מתכנס במ"ש ברור שהוא מתכנס. זה כל מה שצריך להוכיח.
  
 
===תשובה===
 
===תשובה===
−
strictly monotonic כלומר מונוטונית '''ממש'''. זה התנאי לכך שתהיה לה הופכית ואז תוכל לבצע את ההצבה. כמובן שגם העובדה שהפונקציה גזירה נחוצה (על מנת שההופכית תהיה גזירה, חוץ אולי מנקודה אחת).
+
אה.... התבלבלתי בין f_n לf^n.... מצטער.
−
:אופס, התכוונתי לכתוב מונוטונית ממש מלכתחילה ובטעות כתבתי גזירה. בכל מקרה תודה רבה (:
+
 
 +
הכותב מעליי צודק שהטור מתכנס כאשר <math>|f(x)|<1</math>, והוא מתכנס במ"ש כאשר <math>|f(x)|<r<1</math> אבל בגלל שהפונקציה רציפה על קטע סגור ונניח מתכנסת בו אזי היא מקבלת מינימום ומקסימום ושניהם חייבים להיות קטנים ממש מאחד (אחרת היא לא הייתה מתכנסת בהם) ולכן התנאי מתקיים.
 +
 
 +
 
 +
* על מנת להוכיח שהוא מתכנס במ"ש בתנאי למעלה <math>|f(x)|<r<1</math> כל שצריך הוא מבחן הM
 +
<math>|f(x)^n|<r^n</math>.  
 +
 
 +
* על מנת להוכיח שהוא מתכנס עבור התנאי <math>|f(x)|<1</math> כל מה שצריך הוא להסתכל נקודתית על הטור <math>\sum |f^n(x)|=\sum a^n</math> כאשר <math>|f(x)|=a<1</math> וזה כמובן מתכנס.
 +
 
 +
* טריוויאלי שהוא יתבדר בכל מקום אחר.
 +
 
 +
* על מנת להוכיח שהוא לא מתכנס במ"ש אם לפונקציה לא היה מקסימום אבל הsup שלה היה אחד: ניקח סדרה <math>x_n</math> כך ש <math>f(x_n) \rightarrow 1</math> ולכן
 +
<math>\lim_{k\rightarrow \infty} sup|S(x)-S_k(x)|>\lim_{k\rightarrow \infty} |S(x_{n_k})-S_n(x_{n_k)}| = \infty</math>
 +
 
 +
(נבחר את n_k על מנת שההפרשים ישאפו לאינסוף. אנחנו יודעים שזה מותר כי
 +
<math>f(x_n)\rightarrow 1</math>)
  
 
==שאלה==
 
==שאלה==
−
האם גזירה ברציפות משמעותה:
+
אם יש לי פונקציה ואני מפתח לה טור חזקות נניח עם רדיוס 1, איך אני מוודא לאחר הפיתוח שהפונקציה שווה לטור בקטע?
−
1)יש נגזרת
+
וגם פה שאלה 4 כוון כללי אם אפשר...http://moodle.technion.ac.il/file.php/1098/Exams/2004-2005-spring-test-a.pdf
−
2)הנגזרת רציפה
+
−
בלבד?
+
−
תודה
+
  
−
תומר - כמו שאמרת - יש נגזרת והנגזרת הזו היא פונקציה רציפה .
+
===תשובה===
 +
הוא שווה לפונקציה רק ברדיוס ההתכנסות. מה הכוונה איך אתה מוודה? אם פתחת נכון זה חייב להיות שווה - הצעדים שלמדנו לפיתוח פונקציה לטור חזקות הם צעדים בהם השיוון בסוף חייב להתקיים (למשל פונקציה קדומה ששווה בנקודה אחת לטור החזקות [עדיף לבדוק את הנקודה אפס כמובן])
  
  
 +
לגבי השאלה השנייה כבר שאלו אותה, תסתכל בארכיון 17
  
−
ארז ותומר- אתם יכולים להגיד כבר מעכשיו אם יותר השימוש במחשבונים במבחן? בבקשה תרשו- מה אכפת לכם? זה לא יכול להזיק לכם, ואותנו זה מרגיע..... תודה.
+
אבל אתה יודע שאם קיים טור חזקות המקדמים הם אלו של טיילור, למשל הפונקציה f(0)=0 f(x)=exp(-1/x^2)    s
 +
היא שווה לטור החזקות רק באפס למרות שהטור מתכנס בכל הישר (הוא תמיד אפס כי כל הנגזרות באפס הן אפס)
 +
מה שאני שואל זה איך הייתי יודע להבחין שהם שווים רק באפס למרות שהטור מתכנס תמיד, רק שזה לא תמיד לערך הפונקציה?
  
−
:זה מבחן לא בוחן. החלטה של המרצים. מוזמנים לשאול אותם...
 
  
−
תומר - יש סיבה לא להרשות שימוש במחשבון ... יש שאלות שנראה ששימוש במחשבון יכול לעזור לפתור אותן ( כמו במועד ב בבוחן שהיה...) אבל פיתרון מבוסס על חישוב במחשבון לא התקבל ! הנימוקים צריכים להיות מבוססי הוכחה מתמטית ולא חישוב נקודתי .
+
:אל תבלבל. הקטע עם הבדיקה בנקודה זה רק כאשר הוכחת שהפונקציה שלך היא קדומה של טור חזקות כלשהוא ועשית אינטגרציה איבר איבר. באופן כללי למדתם משפט אחד שמאפשר לכם להניח שטור החזקות עם מקדמי טיילור הוא אכן הפונקציה וזה כאשר הנגזרות חסומות (ראה את ההשלמה). במקרים אחרים (כמו זה שתארת) אסור סתם להניח שיהיה שיוויון.
  
−
ארז - מצטרף. מחשבון, מייפל, מטלב, וספרי לימוד הם כלים מאד חשובים למתמטיקאים. בשעת מבחן נבדקת היכולת המתמטית ללא חומרי עזר.
+
כן, אבל בתכלס אם קיים טור חזקות המקדמים שווים למקדמי טיילור
 +
מה שאתה אומר זה להתייחס "כאילו" אנחנו לא יודעים את זה ולעבוד בשיטות אחרות כן? (במקרה והנגזרות לא בהכרח חסומות)
  
−
==בקשר למבחן שהעליתם==
+
:כן. יכול להיות שתשתמש בטריק כי אתה לא יודע להוכיח שהפונקציה שווה לטור חזקות, אבל גם יכול להיות שזה פשוט יהיה קל יותר מאשר לחשב את הנגזרות מכל סדר...
−
קודם כל, תודה רבה :) אבל לא מצאתי אלא שאלה אחת (אם בכלל) על כל החצי הראשון של הקורס, שחשוב לא פחות מהחצי השני (אינטגרלים לא אמיתיים, טורי חזקות וכו'). יש מבחנים שכוללים גם את החומר הזה? אם לא - האם הבוחן הוא אינדיקטור טוב להבנת החומר? כלומר, השאלות שם סה"כ מסכמות את החומר ברמה די גבוהה? ובנוסף, לגבי המועד ב' שהעליתם, שאלה אחת. הוכחנו לפי משפט לבג בדיוק את אותו המשפט, רק שלא נדרש שהנגזרת תהיה רציפה. למה דורשים את זה כאן? בכלל בפתרונות, הם אומרים שg*f (הרכבה) היא הרכבה של פונק' רציפות, אבל לא בטוח בכלל שf רציפה..
+
 
 +
סבבה תודה רבה
 +
 
 +
==שאלה==
 +
 
 +
המבחן ב15:30 נכון? כמה זמן הוא יארך???
 +
 
 +
כן, שעתיים
 +
 
 +
==שאלה==
 +
 
 +
למה הסיגמה של 2*(n+1)*3^n חלקי שורש שלישי של n! מתכנס?
 +
:אתה מתכוון ל<math>\sum \frac{2(n+1)3^n}{\sqrt[3]{n!}}</math>? תקח את השורש הn-י ותקבל 3 חלקי אינסוף כלומר שואף לאפס (הרי <math>\sqrt[n]{n!}\rightarrow \infty</math>)
 +
 
 +
==התכנסות אינטגרלים==
 +
האם האינטגרלים הבאים מתכנסים???
 +
* <math>\int_{0}^{1} \frac{\theta}{\ln(\theta)}d\theta</math>.
 +
* <math>\int_0^1 \frac{dx}{\ln(x)}</math>
 +
* <math>\int_{r=0}^{r=1} \frac{\sin(r^2)}{r}dr</math>.
 +
האם אפשר לומר באינטגרל השלישי ש-
 +
<math>\int_{0}^{1} \frac{\sin(r^2)}{r}dr \leq \int_{0}^{1} \frac{r^2}{r}dr = \int_0^1 rdr = 1/2</math>, ואז עפ"י השוואה???
  
  
 
===תשובה===
 
===תשובה===
−
איך היית מגדיר את שאלות 5 ו6 במועד א' ושאלה 5 במועד ב'?
+
לא לשכוח לבדוק אם האינטגרל הוא אמיתי בכלל או לא. למשל השלישי הוא פשוט בעל אי רציפות סליקה באפס ולכן אינטגרבילי (גם מה שרשמת נכון אבל בלי קשר)
  
−
אני רואה שהם למדו גם חומר שאנחנו לא למדנו, מן הסתם המבחן יהיה על מה שכן למדנו. אי אפשר להסיק ממבחן של שנה מסוימת בדיוק מה יהיה או לא יהיה במבחן. על מנת שמבחנים לא ימשכו שעות תמיד משמיטים חומר מסוים, והחומר הזה יכול להתחלף משנה לשנה וממועד למועד.
+
בראשון ובשני הצד הבעייתי הינו 1. ניתן לבצע מבחן ההשוואה עם <math>\frac{1}{1-x}</math>
  
−
למעשה, אי אפשר בכלל לדעת מראש מה יהיה במבחן :)
+
==שאלה==
  
 +
נתונה פונקציה f(x) בקטע [a,b] ונתון שהיא חסומה על ידי M.
  
−
לגבי השאלה השנייה, יכול להיות שהם לא לימדו לבג בשנה שעברה, ולכן נתנו שאלה חלשה יותר אבל פתירה.  
+
צריך להוכיח שאם f אינטגרבילית זה גורר ש-f^2 אינטגרבילית.
  
−
שנית, אתה צודק f אינה רציפה, אחרת זו שאלה טריוויאלית לחלוטין (כל פונקציה רציפה על קטע סגור אינטגרבילית שם)
+
חסימות זה לא בעיה, אבל הסתבכתי עם התנאי השני
−
:תראו איזה מהירות, שלחתי לרוני את הבעייה שרשמת, והוא כבר החזיר לי גרסא מתוקנת. העלאתי אותה...
+
−
::תודה רבה :). בכל מקרה, אני רוצה לומר תודה על כל הפורום הזה וההשקעה האינסופית..
+
  
−
==תרגיל==
 
−
* נגדיר <math>f(x)=\sum_{n=0}^{\infty}\frac{x^n}{n!}</math>. הוכיחו ש<math>f'(x)=f(x)</math>
 
  
−
(לא ארז/תומר) קודם כל- זהו טור חזקות שמתכנס במ"ש לכל x ממשי. לכן ניתן לגזור איבר איבר. 
+
אני יכול להשתמש במשפט שאם הפונקציות f,g אינטגרביליות בקטע כלשהו אז גם f כפול g אנטגרבילית שם, כאשר במקרה הזה g=f?
−
ואז  <math>f'(x)=\sum_{n=0}^{\infty}\frac{n*x^{n-1}}{n!}=\sum_{n=1}^{\infty}\frac{n*x^{n-1}}{n!}=\sum_{n=1}^{\infty}\frac{x^{n-1}}{(n-1)!}=\sum_{i=0}^{\infty}\frac{x^{i}}{i!}=f(x)</math>.
+
−
השוויון השני נכון כי עבור n=0 נקבל אפס. בשוויון הלפני אחרון החלפתי משתנה: <math>i:=n-1</math>
+
  
 +
:(לא ארז/תומר) ענו כבר על השאלה הזאת... לדעתי אי אפשר להשתמש במשפט, למרות שהוא נכון, כי אז התרגיל טריוויאלי.
 +
:הנה ההוכחה- יהי אפסילון גדול מאפס. בכל קטע  g(x1)-g(x2)=(f(x1)+f(x2))*(f(x1)-f(x2)<2M*W כאשר W היא התנודה של f בקטע. (g מוגדרת כ f בריבוע). מאינטגרביליות f קיימות חלוקה עבורה סכום התנודות קטן מאפסילון חלקי 2M. ועבור אותה חלוקה בפונקציה g סכום התנודות יהיה קטן מאפסילון.
  
−
:זה שאתה לא אני זה לא מפתיע, כי אני רשמתי את השאלה :) רק דילגת על חלק עיקרי בהוכחה, מדוע הטור מתכנס במ"ש לכל x ממשי? זה נכון בכלל?
+
תומר - ומה עם מידת נקודות אי רציפות ? אם אתם יודעים שהפונקציה אינטגרבילית זה אומר שמידת קבוצת נקודות האי רציפות שלה היא אפס . מה עם נקודות האי רציפות של הפונקציה בריבוע ? האם היא מוכלת בזו של הפונקציה המקורית ? ואם כן מה זה אומר על מידתה ? ...
  
−
(מישהו אחר) זה נכון כי לפי המבחן של קושי עם הגבול העליון, הגבול של שורש nי של n! הוא אינסוף, ולכן הגבול של 1 חלקי זה הוא 0, ולכן הרדיוס הוא אינסוף. ואז אפשר להמשיך כמו שהבחור הקודם הראה, או להראות שan שווה בדיוק לפיתוח לטור חזקות של e^x שמקימת שהנגזרת שווה לפונקציה
+
==שאלה==
 +
צריך להוכיח שהטור הבא מתכנס במ"ש.
 +
f(x)= sum from 0 to infinity of (e^-nx)* cos(nx) s
  
−
::::נתבונן בפונקציה <math>g(x)=e^x</math> בקטע הסגור <math>[-r,r]</math>.
+
בכל קטע (a, infinity] כאשר a>0
−
לכל x בקטע ולכל n טבעי מתקיים
+
  
−
<math>|f^{(n)}(x)|=|e^x|<e^r</math>
+
ניסיתי עם מבחן ה- m ולא הצלחתי.
 +
מישהו?
 +
אפשר להשוות עם e^-n במבחן הM לא?
  
−
לכן בכל קטע סגור כזה ניתן לפתח את הפונקציה לטור חזקות, שזה בדיוק הטור בשאלה.
+
:(לא ארז/תומר) אני חושב שצריך להשוות עם e^-an ...
−
הטור מתכנס בכל קטע סגור כזה, לכן הוא מתכנס (נקודתית) על כל הישר הממשי, כלומר יש לו רדיוס התכנסות אינסוף.
+
−
לכן הוא מתכנס במ"ש בכל קטע סגור על הישר.
+
−
לכן ניתן לגזור איבר איבר כמו למעלה.
+
  
 +
עם e^-n וזה עובד. עכשיו בסעיף הבא הם רוצים להוכיח/להפריך שf(x) שזה הסכום הוא פונקציה רציפה ב(o, infinity). הבעיה זה שזה קטע פתוח ולא סופי.. עדין אפשר להשתמש במשפט על טור של פונקציות רציפות המתכנס במ"ש?
  
−
* אי אפשר להשתמש בפיתוח של e^x ובעובדה שהוא הנגזרת של עצמו, הרי זה מה שאתם מתבקשים להוכיח.
+
:תמיד משתמשים באותו טריק (לא התעמקתי בשאלה, מקווה שרלוונטי) אם ההתכנסות היא במ"ש על כל תת קטע סגור וסופי אז יוצא שפונקצית הגבול רציפה בכל נקודה בלי שתהיה התכנסות במ"ש על הקטע האינסופי/פתוח כולו.
−
*רדיוס ההתכנסות הוא אכן אינסוף ולכן טור החזקות מתכנס במ"ש על כל קטע סופי, ולכן מותר לגזור איבר איבר על כל קטע סופי. זו אכן התשובה. (זה לא אומר שהטור מתכנס במ"ש על כל הממשיים).
+
  
−
למה אי אפשר? אם אני מראה שאת e^x אפשר לפתח לטור חזקות והרדיוס התכנסות שלו זה אינסוף, ומראה שהטור חזקות זה בדיוק הטור הזה. זה לא אומר שהנגזרת שווה לפונקציה כמו e^x?
+
== תרגיל 11 ==
 +
מישהו יכול לכתוב שוב את הלינקים לתרגילים שבתרגיל 11, הלינקים לא עובדים לי. 
  
−
:הנחת שהנגזרת של e^x הינה e^x כאשר הראת שהטור הזה הוא הפיתוח של e^x. אבל זה מה שצריך להוכיח...
+
:ארכיון 16...
  
−
::איך מראים שרדיוס ההתכנסות הוא אינסוף?
+
==שאלה==
−
<math>\overline{\lim_{n\rightarrow \infty}} \frac{1}{\frac{1}{\sqrt[n]{n!}}}=\infty</math> מכיוון ש<math>\lim \sqrt[n]{n!}=\infty</math>
+
מתי יפורסמו ציוני התרגיל והבוחן (אני יודע שיש לנו אותם, הכוונה עם פקטור, וציוני תרגיל 8/10 אם אני לא טועה) והאחוזים מהציון הסופי?
  
−
:::יש לי סתם שאלה, בלי קשר לתרגיל הזה - אם, באותו אופן, היה יוצא שהרדיוס הוא 0, האם זה מספיק, וכל שנותר הוא לבדוק התכנסות בנק' x=0?
+
מצטרף!!
−
*מספיק בשביל מה? זה אומר שהטור לא מתכנס בשום מקום פרט לנקודה. לכן הוא לא רציף ולא גזיר ולא מעניין. אין מה לבדוק התכנסות בנקודה אפס, זה תמיד מתכנס שם לקבוע a_0
+
  
−
::::אבל איך חישבת את הגבול הזה?
+
תומר - יפורסם בשעות הקרובות . אני עצמי עוד בודק תרגילים שהוגשו באיחור(!) . סבלנות .
 +
יש חדש?
  
−
*זה תרגיל מאינפי אחד. אתה מקטין את חצי מהאיברים של n! לאחד, ואת החצי השני אתה מקטין לn/2 וסה"כ אתה מקבל <math>n!>(\frac{n}{2})^{\frac{n}{2}}</math> ולכן <math>\sqrt[n]{n!}>\sqrt[n]{(\frac{n}{2})^{\frac{n}{2}}}=\sqrt{\frac{n}{2}}\rightarrow \infty</math>
+
==שאלה==
 +
אוקי, נניח ויש לי סדרת פונקציות, ואני צריכה לבדוק לאילו ערכי אלפא הסדרה מתכנסת במ"ש ב0,אינסוף (חצי סגור) וב[0,1]. קודם כל בדקתי את 0 אינסוף, והגעתי לזה שעבור אלפא קטן מ2 ==> הסדרה מתכנסת במש.
 +
התחום השני, [0,1], מוכל בתחום הראשון - ונניח שהגעתי לזה שהסדרה מתכנסת במש בתחום זה עבור אלפא גדול מ2-. מכיוון שהתחום מוכל, זה אומר לי גם שבפרט הסדרה מתכנסת במש גם עבור אלפא קטן מ2, וביחד - עם שתי המסקנות האלה - מתכנס לכל אלפא?
  
−
דבר אחר, ניתן להראות שלכל x0 ממשי טור המספרים שמתקבל ממנו מתכנס, ולכן הטור מתכנס נקודתית בכל הישר, ובפרט במ"ש בכל קטע סגור בו.
 
  
−
*איך התכנסות בכל נקודה גוררת התכנסות במ"ש? זה מאד לא נכון. ההתנכסות על כל קטע סופי היא במ"ש מכיוון שזה טור חזקות עם רדיוס אינסוף. טור חזקות מתכנס במ"ש על כל קטע סופי שקטן ממש מהרדיוס שלו.
+
===תשובה===
−
-אבל אם הטור מתכנס בכל נקודה, זה בדיוק כמו לאמר שהרדיוס שלו הוא אינסוף...
+
לכאורה כן, אני לא מבין מה השאלה. הרי ברור שאם זה מתכנס במ"ש לכל אלפא גדול ממינוס 2 או קטן משתים בפרט זה מתכנס לכל אלפא. השאלה האמיתי היא אם החישובים שלך נכונים.
−
::כן. אם זו הכוונה שלך אז אתה צודק. (חשוב לפרט שזה טור חזקות, ולכן הרדיוס הוא אינסוף ולכן הוא מתכנס במ"ש על כל קטע סופי).
+
:השאלה היא כזו - הוכחתי שעבור אלפא קטן מ2 זה מתכנס במ"ש ב0,infinity. רק רציתי לוודא שזה אומר שעבור אלפא קטן מ2 זה מתכנס במ"ש גם ב[0,1]. זה נכון?
  
−
:::
+
::הדגש הוא על הקטע הסגור? אם יש התכנסות באפס אז כן, אם לא אז לא
−
::::אפשר לומר שהגבול שצריך לחשב הוא הממוצע הגיאומטרי של הסדרה <math>a(n):=n</math>, ולכן שאיפת הסדרה לאינסוף גוררת את שאיפת הממוצע לאינסוף לפי משפט, לא?.
+
:::כן, מדובר על קטעים סגורים. תודה:)
−
*אני לא זוכר משפט כזה, יכול להיות שאתה צודק..
+
  
−
==שאלה - טורי חזקות==
+
אני טועה או שבהתחלת ההרצאה האחרונה רוני אמר שבטווח שבין רדיוס ההתכנסות לבין המינוס שלו(לא כולל הוא עצמו)- הפונקציה מתכנסת, ואח"כ הוא  אמר שהיא גם מתכנסת במ"ש בכל קטע סגור שמוכל בקטע הזה.....?
−
יש איזו נקודה שלא לגמרי נגענו בה בתרגול ההשלמה - טורי חזקות, כאשר החזקה היא, למשל, <math>n^2</math> , או <math>2^n-1</math>. מתי כדאי להפריד למקרים של מקדמים (ואז הסופרימום הוא מתי שיש מקדם), ומתי כדאי להציב, למשל, <math>t=x^{n^2}</math> ? (בתרגיל יש רק דוגמא לזוגיים ואי-זוגיים)
+
:זה נכון לגבי טור חזקות, אני לא בטוח איך זה קשור פה.
 +
 
 +
::יש עוד מקום עם רדיוס התכנסות חוץ מטור חזקות??? ושאלתי כי זה נראה לי מוזר להוכיח משהו ואז להוכיח משהו ותר חזק במקום להוכיח ביחד. למה פה? איפה עוד אני יכול לכתוב???
 +
 
 +
:::לא פה בפורום, התכוונתי פה בשאלה הזו... רדיוס התכנסות זה מושג של טור חזקות, וכאן מדובר על סדרת פונקציות.
 +
 
 +
==שאלה==
 +
מצטער על הבורות רגע לפני המבחן- מה זה גזירה איבר-איבר? ואינטגרציה איבר איבר? בבקשה שלא יהיה מסובך....
  
 
===תשובה===
 
===תשובה===
−
קשה קצת לענות בלי לראות דוגמא, צריך להשתמש בשיטה שבעזרתה תצליח לפתור את התרגיל.
+
נניח ויש לך טור מתכנס <math>g=\sum f_n</math>. השאלה היא מהי הנגזרת של g. אם מותר לגזור איבר-איבר אזי <math>g' = \sum f_n'</math>. שים לב שזה לא תמיד נכון, רק כאשר המשפטים מאפשרים לגזור איבר-איבר.
  
−
תומר - עשינו דוגמאות בהן למשל החזקות היו רק האי זוגיים למשל , והצגנו דרך להתייחסות למקרים כאלו - מופיע בסיכום תירגול ההשלמה הסרוק . בנוסף נשים לכם דוגמאות נוספות .
+
אינטגרציה זה דומה <math>\int g = \sum \int f_n</math>
  
 +
==שאלה==
 +
אם טור חזקות מתכנס גם בR וגם בR-, זה אומר שהוא מתכנס במ"ש ב[0,R] וב[-R,0] ואז זה אומר שהוא מתכנס במ"ש ב[-R,R]?
  
−
==תרגיל 8 שאלה 2==
+
===תשובה===
−
בתרגיל 8 שאלה 2: לא היה אפשרי לפתור כך?: f רציפה ולכן יש לה קדומה,נסמנה g. האינטגרל של f מa עד b הוא בעצם הערך של g בנקודה b פחות ערכה בנקודה a. הפונקציה g היא גזירה, ולכן מתקיים עבודה תנאי לגראנז',(f היא הנגזרת של g): ולכן קיימת נקודה c עבורה ערך הפונקציה f בנקודה שווה לערך של g בנקודה b פחות ערכה בנקודה a חלקי b-a. מ.ש.ל.
+
כן. באופן כללי אם טור מתכנס במ"ש בשני קטעים סגורים צמודים הוא מתכנס במ"ש באיחוד הקטעים. כי מהירות ההתכנסות עבור אפסילון היא המקסימום בין שני הn_0 של שני הקטעים.
  
−
לא יותר קל להוכיח ככה?
+
== :)==
 +
שיהיה בהצלחה לכולם! לא פחות מ100 :)
  
−
:זו הוכחה תקינה.
+
תומר - מצטרף ! שיהיה בהצלחה לכולכם - במבחן הזה ובכל אלו אחריו :)
 +
:תודה, ותודה לכם על סמסטר נפלא (עד כמה שהיה אפשר. אינפי, אתם יודעים). תודה על התרגולים המצויינים, אפילו שהיו יותר מידי אנשים בכיתה... ותודה על ההשקעה בנו ועל כל העזרה (האתר, וכל דבר אחר). אולי תהיו מתרגלים שלנו באינפי 3?
 +
:ושיהיה בהצלחה לכולם!
  
−
==שאלה- לגבי נושאי הקורס שהעלתם==
+
==לארז ולתומר==
−
האם למדנו בקורס את פונקציה בעלת השתנות חסומה, ומשפט ז'ורדן?
+
רגע אחרי המבחן, וכמה ימים לפני שהאתר יתחיל לשמש, כנראה, תיכוניסטים תמימים שצעירים מאתנו בשנה, ואתם אורזים את הכל בשבילם, רציתי לומר לכם, לשניכם במ"ש, ת-ו-ד-ה  ר-ב-ה!! על כל ההשקעה, הזמן, הרצון והכוח שהיה לכם להתמודד עם שתי קבוצות רועשות כמו שלנו, ועוד בקורס קשה כמו אינפי 2! שיהיה לכולנו המון בהצלחה בהמשך!
−
לא זכור לי שלמדנו...
+
  
−
:הקבוצה של רוני למדה. הקבוצה של שיין לא?
 
−
למיטב ידיעתי, ולאחר בדיקה בקלסר,
 
−
לא למדנו את שני הנושאים הנ"ל, אשמח אם עוד מישהו יוכל לאשר זאת...
 
  
−
אכן, לא למדנו את הנושאים האלו.
+
מצטרף בהחלט, המון תודה לשניכם, ואולי נתראה בהמשך...
 +
:מצטרפת.. ממש תודה על הכול! מה נעשה בלי Math-wiki..
 +
מצטרף! זה לא מובן מאליו... ועם זאת, מתי נדע כמה פקטור יהיה(בטוח יהיה...!!)
  
−
אז מה נסגר? האם החומר ירד מהמבחן? לא נוכל ללמוד אותו לבד?!
+
::תודה רבה על כל האיחולים - המתרגלים. (בלי קשר, אני אפרסם עוד כמה דקות פתרון למבחן בדף הקורס)
−
נשמח לקבל עדכון בעניין... תודה!
+
  
−
:מה שלא למדתם בהרצאה, לא יופיע במבחן.
 
  
 +
אני מסכים לגמרי עם כל השאר. אתם באמת השקעתם את כל כולכם בנו ובהצלחה שלנו. באמת רואים שאכפת לכם מאיתנו למרות כל הקיטורים, בקשות לדחיות, התחננויות ולפעמים אף בכי P=
 +
אני רק לא מבין משהו אחד. ניסיתי להבין מה הייתה התועלת בשיעורי חזרה ובתרגולים הנוספים שעשיתם, ואני לא מוצא בהם תועלת למבחן... לא עשינו אפילו תרגיל אחד שהיה אפילו דומה לשאלות שהיו במבחן (אני לא מתכוון לשאלות בדיוק כמו שהיו במבחן, אבל לפחות בסגנון ובנושאים)...  כאילו שמתם דגש בשאלות לא דומות למבחן בשביל מה? הרי ראיתם את המבחן כבר...  לי אישית היה די קשה להגיע לבר אילן,לתירגולים, באותו היום אבל הגעתי בכל זאת כי חשוב לי להצליח במבחנים (כמו לכולנו), אבל בתכלס שאני מסתכל על היעילות שלהם לאחר המבחן לא עזר בכלל, אלא להיפך.
 +
כל מה שאני מנסה להגיד, זה שבתרגולי חזרה לפני מבחן, תעזרו קצת יותר בכך שתתרגלו אותנו נכון, ולא לבלבל לנו את השכל עם שאלות לא קשורות בכלל... אחר כך מתלוננים שאנחנו לא מקבלים ציונים נורמלים ואתם נאלצים לעשות פקטור סתם!
 +
תודה על הכול (וזה בשיא הכנות) כי באמת השקעתם בנו 
  
−
במבחן שהועלה לאתר, במועד ב', לא היה אפשרי ויותר קל לפתור בדרך הבאה?:
+
===תשובה===
−
הפונקציה רציפה ולכן חסומה- כמו שכתוב בפתרון.
+
אני אענה לשאלה שלך בשני מישורים
−
ואז- אם הפונקציה רציפה בקטע סגור ולכן חסומה- אז נסמן בp את ההפרש בין הערך הכי גדול לערך הכי קטן שלה. ואז צריך להוכיח שלכל a>0 ולכל חלוקה T קיים r שגדול מדלתא T כך ש:סיגמה, כאשר i רץ מ1 עד n של Mi-mi כפול דלתא Xi קטן מa, נכון?
+
* הראשון והחשוב יותר: מטרתנו הראשונה והעיקרית כמורים הינה ללמד אתכם מתמטיקה ו'''לא''' להכין אתכם למבחן. הכנה למבחן הינה משנית (אמנם חשובה גם כן). קשה להגיע לבר אילן גם במהלך הסמסטר, אך אתם מגיעים על מנת ללמוד. הסיבה שאנו רואים את המבחן קודם לכן היא בעיקר על מנת לוודא איכות שלו (שאין טעויות, רמה סבירה וכדומה), עלינו להעביר שיעורי חזרה כאילו לא ראינו את המבחן.
−
ואז נגיד שMi-mi קטן מp ודלתא Xi קטן מr. ולכן הסיגמה היא בעצם קטנה מ- n*r*p. ולכן נבחר את r להיות a/n*p. ואז זה שווה לa וסיימנו.  שיניתי את האותיות המקובלות אבל זה אותה כוונה....
+
  
 +
*שנית, אני אפריך לחלוטין את הטענות שהעלאת:
 +
**שיעור ההשלמה היה חלק מחומר הקורס וכלל שאלה שהופיעה כלשונה במבחן! (הוא היה לפני שראינו את המבחן). אז כבר 20 נקודות מתנה על שיעור ההשלמה והחומר שהועלאה לאתר (אני לא העברתי את השאלה פרונטלית אבל תומר כן). אמרנו לכם לקרוא את שיעור ההשלמה.
 +
**שיעור החזרה כלל שאלה כמעט זהה לחלוטין לשאלה 3 מהמבחן (אני העברתי אותה ותומר לא).
 +
**יום או יומיים לפני המבחן עניתי באתר על שאלה דומה לשאלה 2 במבחן, והדגשתי דברים שלא היו בשאלה המקורית כי ידעתי שזה יעזור למבחן.
 +
**שאר השאלות, בוודאי היו דומות והתעסקו בנושאים דומים...
  
−
ההוכחה הזאת לא אומרת שכל פונקציה חסומה היא אינטגרבילית??? משהו כאן בטוח לא נכון, אבל מה? גם פונקצית דיריכלה יוצאת כאן אינטגרבילית, פשוט להציב p=1.......
 
  
−
: אני לא לגמרי מצליח לעקוב אחרי דרך הרישום הזו אבל:
+
מעבר לכך, תודה על ההכרה בעבודה שלנו. תאמינו לנו שמה שעכשיו נראה לכם לא כיף, בעתיד אתם תראו כאתגר שהצלחתם בו. החיים הם לא מיטת שושנים, ומי היה רוצה לישון במיטת שושנים בכלל? זה דוקר!
−
*הכותב מעליי צודק, כביכול הוכחת שכל חסומה היא אינטגרבילית
+
:זה לא רק דוקר, זה גם צמיגי :P
−
*אני חושב שהבעייה היא שאתה מגדיר את r להיות תלוי בn. אני לא בטוח מה זה r אבל אני דיי בטוח שהוא לא צריך להיות תלוי בn :)
+
::מתי יעלו ציוני תרגיל?
 +
 
 +
:::אנחנו נעלה אותם היום
 +
==יש לי שאלה==
 +
האם בשאלה 4ב במבחן היה אפשר להגיד שההתכנסות היא ל0 כי תנאי הכרחי להתכנסות הטור היא שאיפת האיבר הכללי לאפס
 +
(הוכחה של התכנסות לאפס לא התכנסות במש)?
 +
 
 +
===תשובה===
 +
כן, זה מוכיח בהחלט התכנסות נקודתית לאפס (ולא במ"ש כפי שציינת)
  
 
==שאלה==
 
==שאלה==
−
תהי f פונקציה רציפה ב[a,b] ונניח שקיימת חלוקה P של [a,b] שעבורה הסכום העליון שווה לאינטגרל מa עד B של הפונקציה. צריך להראות כי בהכרח f קבועה ב[a,b].
 
−
רעיון ?
 
  
−
:נניח בשלילה שפונקציה אינה קבועה. נותר להראות שאם קיימת חלוקה כזו, קיים עידון שלה בעל סכום עליון קטן ממש יותר בסתירה.
+
למה מופיע לי ציון 0 בתרגיל מספר 2 אם הגשתי אותו? :S
 +
 
 +
:זו שאלה פילוסופית?
 +
 
 +
==הודעה==
  
 +
יש ציונים!!
 +
== מבחן ==
 +
היה פקטור במבחן? ואם כן של כמה?
  
−
::(לא ארז/תומר)אם אתה רוצה הוכחה מלאה:  נתבונן בקטע החלוקה ה-i-י. נניח בשלילה שקיימת בקטע זה נקודה שערך הפונקציה בה קטן ממש מערך הפונקציה המקסימלי בקטע. ערך הפונקציה בכל x בקטע קטן שווה לערך המקסימום בקטע, וכיוון שיש נקודה בה אי השיוויון חזק, נקבל בתוספת הנתון על הרציפות שיש אי שיוויון חזק באינטגרלים. כלומר, אינטגרל על הערך המקסימלי גדול ממש מאינטגרל על הפונקציה, בקטע המדובר. כיוון שבכל קטע חלוקה אחר מתקיים שערך הפונקציה המקסימלי באותו קטע גדול שווה לכל ערך אחר בקטע (לפי הגדרת המקסימום, שקיים כי זו פונקציה רציפה בקטע סגור), אם נסכום את כל אי השוויונות האלו בתוספת אי השוויון החזק בקטע ה-i-י, נקבל שהאינטגרל על הפונקציה ב [a,b] קטן ממש מהסכום העליון של החלוקה P,  בסתירה לנתון. לכן בקטע ה-i-י החלוקה קבועה. זה נכון לכל i ולכן בכל אחד מקטעי החלוקה הפונקציה קבועה. כעת נתבונן בנקודות החלוקה של P. לכל נקודה כזו (חוץ מהקיצוניות) מתקיים שהגבול של הפונקציה כש-x שואף לנקודה מימין הוא הערך הקבוע של הפונקציה בקאע שמימין לנקודה. ובאותו אופן הגבול משמאל יהיה הערך הקבוע בקטע שמשמאל לנקודה. הפונקציה רציפה בפרט בנקודות החלוקה, לכן הגבולות החד-צדדיים שווים כלומר הערכים הקבועים של הפונקציה בקטעי החלוקה הימני והשמאלי לנקודה שווים. זה נכון לכל נקודה בחלוקה ולכן הפונקציה קבועה. מש"ל.
+
מצטרף לשאלה... מאוד חשוב לנו לדעת האם להגיש ערעור או שלא.... והאם לגשת למועד ב או לא
 +
בקיצור ממש חשוב לנו לעת האם היה פקטור...
  
−
==שאלה- גזירת טור חזקות==
+
:תשאלו את המרצים, אנחנו (המתרגלים) לא יודעים.
−
הוכחנו בהרצאה משפט שאומר שניתן לגזור טור חזקות איבר-איבר בכל נקודה בתחום התכנסותו.
+
−
הניסוח של המשפט לא דורש התכנסות במ"ש, רק עושים בזה שימוש בהוכחה.
+
−
לאור המשפט הזה- האם בתרגיל שהועלה לאתר (שצריך להוכיח שהפונקציה שווה לנגזרת), אפשר פשוט לגזור איבר איבר (כי זה טור חזקות)?
+

גרסה אחרונה מ־11:47, 1 בספטמבר 2010

\lim_{n\rightarrow\infty}f_n

הוראות

כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:

== כותרת לשאלה ==

לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין

ארכיון

ארכיון 1 - תרגיל 1 ו2

ארכיון 2 - תרגיל 3

ארכיון 3 - תרגיל 3

ארכיון 4 - תרגיל 4

ארכיון 5 - תרגיל 4,5

ארכיון 6 - תרגיל 6

ארכיון 7 - (מי עוקב)

ארכיון 8

ארכיון 9 - לקראת הבוחן

ארכיון 10 - פוסט בוחן

ארכיון 11 - תרגיל 9

ארכיון 12 - תרגיל 9

ארכיון 13 - תרגיל 10

ארכיון 14 - תרגיל 10

ארכיון 15 - תרגיל 10

ארכיון 16 - לקראת המבחן

ארכיון 17 - לקראת המבחן

שאלות

שאלה

יהיה במבחן פונקציות עם שתי משתנים?

לא שידוע לי, אם המרצה אמר שיהיה אז יהיה, אם לא אז לא

תומר - מה פתאום שיהיה משהו שלא למדתם ??? הגיון חבר"ה , הגיון !

שאלה

תחת אילו תנאים ניתן לומר שאינטגרל על סכום אינסופי של פונקציות שווה לסכום האינסופי של האינטגרלים של הפונקציות? תודה

תומר - מפנה אותך לנוסח משפטים המתאימים ! יש משפטים שמתארים תנאים מספיקים לכך . ייתכן שיהיו מצבים נוספים שזה יתקיים אבל אז צריך לבדוק כל מקרה לגופו.

שאלה

נניח יש לי טור פונקציות שרץ על fn (הסדרה המזהה שלו). למה אם הטור |fn| מתכנס במ"ש בI, אז גם הטור המקורי מתכנס במ"ש בI?

  • נקודתית זה ברור מאינפי 1. לבמ"ש ההוכחה דומה. שארית הטור לא בהחלט קטנה משארית הטור בהחלט, כלומר הטור לא בהחלט מתכנס מהר יותר מאשר הטור בהחלט.

ועוד שאלה: אם יש לי סדרת פונ' fn כך ש|fn| מתכנסת לפונ' גבול כלשהי f במ"ש, האם זה אומר שfn המקורית מתכנסת לf1 כלשהי במ"ש?

  • ברור שלא.... אינפי 1. 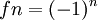fn=(-1)^n לא מתכנס בכלל, אבל הערך המוחלט מתכנס במ"ש.

יש טעות בסיכום במשפט פרמה, לא? המשפט הראשון בעמוד הראשון של הסיכום...התנאים לא צריעכים להיות הפוכים???

  • נכון מאד, הסרתי את הסיכום. המשפט אומר שאם יש מקסימום/מינימום והפונקציה גזירה הנגזרת הינה אפס. בוודאי שאם הנגזרת אפס אין שום הכרח שיהיה מינימום/מקסימום (לדוגמא x^3).

שאלה:איך מוגדר אינטגרל של פונקציה ממינוס אינסוף לאינסוף? הגבול כאשר c רץ לאינסוף של אינטגרל של הפונקציה מ c- עד c או פשוט פיצול לשני אינטגרלים לא אמיתיים ואז כל אחד שואף בקצב שלו? זה משנה כי במקרה של פונקציה איזוגית-למשל x באפשרות הראשונה זה 0 ובשניה אינסוף פחות אינסוף שזה מתבדר.....(נכון?)תודה.

  • הוא מוגדר בתור הסכום של שני אינטגרלים לא אמיתיים. האינטגרל על הפונקציה x למשל מתבדר.


למה אם f פונקציה רציפה, מחזורית ואי-שלילית בממשיים(f אינה זהותית אפס) אז הגבול של f(x)/x^3 אינו אפס כאשר x שואף לאינסוף?? הרי f חסומה מהנתונים,לא? רוני נתן שאלה כזאת ואמר להוכיח שהאינטרגל של f(x)/x מ1 עד אינסוף מתבדר. ואם הגבול שאמרתי מקודם שווה ל0 אז לפי מבחן ההשוואה האינטגרל מתכנס, אז כנראה שהגבול איננו 0,למה???

תשובה

תומר - כמה שאלות , כמה שאלות ! :) לשאלה הראשונה על התכנסות עם ערך מוחלט גוררת התכנסות בלי , במידה שווה - ראה משפט שהוכחתם . או - אפשר לנסות לבד פשוט ביישום של קריטריון קושי להתכנסות במ"ש ! .

אינטגרל ממינוס אינס' לאינס' מוגדר על ידי פיצול באיזו נקודת ביניים - אבל בכל אופן כאשר הגבולות שלהם - אחד עם פרמטר לאינסוף ושני עם פרמטר למינוס אינסוף - הם לא תלויים אחד בשני ! ובטח לא ממינוס סי לסי כאשר סי שואף לאינסוף . זהו אינטגרל שקיים בשימושים אבל יש לו שם - PRINCIPAL VALUE - אבל זה לא האינטגרל בקורס שלנו !!! .

לגבי שאלה אחרונה - תן בבקשה את ניסוח השאלה המלא כדי שאוכל להתייחס .

שאלה מסודרת

נתונה פונקציה fרציפה,מחזורית ואי-שלילית ב-R. היא אינה זהותית 0.הוכח: האינטגרל של f(x)/x מ-1 לאינסוף מתבדר. תוכל גם להגיד לי למה אי אפשר להוכיח שזה מתכנס עם שימוש במבחן ההשוואה השני? כי f לפי הנתונים חסומה,לא? ואז הגבול של (f(x)/x)/x^2 שווה לאפס ולפי המבחן f(x)/x מתכנס, כי האינטגרל של x^2 מתכנס...

תשובה

(לא ארז/תומר) נראה לי שהטעות שלך היא כזו , כשאתה עשית את מבחן ההשוואה, עשית את זה עם הפונ' x^2 והאינטרל של זה מתבדר בקטע 1 עד אינסוף (אתה מתבלבל עם 1/x^2).

אבל אמרתי בקטע 1 עד אינסוף...לא מאפס!
הוא העיר לך על הפונקציה ולא על הקטע. x^2 זו פונקציה ששואפת לאינסוף ובפרט אינה אינטגרבילית על הקטע האינסופי.

ובנוגע להוכחה , אני עשיתי את זה בדרך הבאה:

נסמן את המחזור של F כ-T, אנחנו יודעים שהפונ' אינה זהותית אפס, לכן יש נקודה X0 בקטע [1,1+T] כך ש- (f(x0 שווה ל-M גדול ממש מאפס. מכיוון ש-F רציפה יש סביבה [a,b] של X0 כך שכל ס בקטע מקיים f(x)>M/2 (או אפילו גדול שווה, זה לא משנה) וכעת, מכיוון ש-F אישלילית , נגדיר פונקציה חדשה G להיות M/2x בכל קטע מהצורה [a+n*T,b+n*T] כאשר n טבעי ואפס בכל נקודה אחרת.

ברור כי שתי הפונ' אי שליליות, אינטגרביליות בכל קטע מהצורה [one,R] כש- R>1 (F רציפה בכל קטע כזה, ול-G יש מספר סופי של נקודות אי רציפות מהסוג המתאים) ולכן אם האינטגרל של G בטע 1 עד אינסוף מתבדר, כך גם האינטגרל הלא אמיתי של F.

ועכשיו, להראות שהאינטגרל של G בקטע 1 עד אינסוף מתבדר, זה לא כזה מסובך (אני עשיתי לפי קריטריון קושי, אבל אני בטוחשאפשר בעוד דרכים, ואין לי כח לכתוב את זה) ובסה"כ קיבלנו שהאינטגרל של f(x)/x

שאלה

למה במבחן ההשוואה הראשון רוני ציין שאם 0<g ו f>g והאינטגרל של f מתכנס(לא אמיתי, בשנ הסוגים הוא אמר ככה...) אז האינטגרל של g מתכנס. הוא לא אמר שאם g מתבדר גם f מתבדר,זה לא נכון??

תשובה

המשפט השני הוא היקש לוגי מהראשון. לא יכול להיות שf יתכנס אבל g יתבדר, לכן אם g מתבדר אזי f מתבדר.

שאלה

בתרגיל 11 שאלה 3 - לעוד מישהו יצא רדיוס התכנסות אפס?

[לא תומר או ארז] לי דווקא יצא 1

שאלה

אם אני צריכה להוכיח שפונק' כלשהי היא אינטגברילית רימן, והראיתי שהסכום רימן שלה לכל חלוקה מתאימה ולכל בחירה אלפא חסומה בין הסכום רימן של פונק' אינטגרבילית(!) אחרת פחות אפסילון, ואותו סכום ועוד אפסילון. האם זה מראה לי שהפונק' שלי אינטגרבילית גם? ויותר מזאת, שואפת לסכום I של אותה הפונקציה השניה?

הסכום רימן של הפונקציה האחרת עבור אותה חלוקה? ומה זה האפסילון הזה? במה הוא תלוי?

שאלה

נתון כי f אינטגרבילית וחסומה ע"י M. צ"ל שf^2 אינטגרבילית באותו קטע. יש דרך להראות את זה לא ע"י הרכבת פונקציות (שבדרך זו הנתון ע"י החסימות מיותר)? מהי הדרך?

הנתון על חסימות מיותר איך שלא תסתכל על זה, שכן זו פונקציה אינטגרבילית (ולכן חסומה)

אבל יש דרך להראות את זה חוץ מהרכבה של פונקציה רציפה ופונקציה אינטגרבילית?

תומר - מידת קבוצת נקודות אי הרציפות של הפונקציה החדשה היא אפס ? ...

(לא ארז/תומר) כן יש פיתרון אחר, והוא בעזרת תנאי רימן לאינטגרביליות. f^2 חסומה (ברור), ונותר להראות את התנאי השני. בקשר אליו, קל להראות ש

w(f^2)<= w(f)*2*M (כאשר w הוא התנודה בקטע), ומכאן קל להמשיך.

מראים את זה כך, לכל x1,x2 בקטע כלשהו מתקיים: f(x1)^2-f(x2)^2<=(f(x1)-f(x2))*(f(x1)+f(x2)), ומכאן זה ברור

שאלה

התבקשתי להביא דוגמה לסדרת פונק' fn רציפות ב[0,1] כך שfn(x)-->0 לכל X בתחום, אך האינטגרל של fn מ0 עד 1 אינו שווה ל0. - האם הפונקציה x^n(x^n-1) qq מקיימת את הדרוש? הפונק' אכן רציפות ב[0,1], פונקצית הגבול היא 0, אבל האינטגרל יוצא, אם אני לא טועה, 1/n פחות 1/(2n+1)..

תשובה

אתה בטוח שהאינטגרל שונה מאפס ולא שואף לאפס? כי כמעט כל סדרה שתבחר תעמוד בתנאי הראשון (למשל הסדרה של הפונקציות הקבועות \frac{1}{n}).

אם אתה רוצה סדרה שהאינטגרל עליה אינו שואף לאפס, קח סדרה של פונקציות הבאה: הגרף של הפונקציה ה-n הוא משולש עם בסיס \frac{1}{n} בגובה 2n וכל שאר הפונקציה היא אפס. הסדרה הזו שואפת לאפס (כמובן שלא במ"ש) והאינטגרל על כל פונקציה בסדרה הוא תמיד 1.

שאלה

נראית נחמדה. f:[0,1] ---> R היא פונקציה רציפה אי שלילית המקיימת f(x)<=sinx לכל x בתחום. צריך למצוא את כל פתרונות המשוואה: cosx+quad(f,0,x)-1=0. (קוסינוסX ועוד האינטגרל של f מ0 עד x פחות 1 = 0.) מעבר לעובדה שx=0 הוא פתרון אחד של המשוואה, לא הצלחתי להוכיח שלא קיימים עוד פתרונות/למצוא פתרון נוסף. ניסיתי להניח שקיים ולהשתמש במשפט רול, ניסיתי להשתמש בזה שאי שיוויון ברמת הפונק' ==> אי שיוויון ברמת האינטגרל אבל בסופו של דבר לא הגעתי למשהו שמוכיח. יש רעיון למישהו?

מישהו??


אם f=sinx אזי זו הפונקציה הקבועה אפס. אם f קטן ממש מהסינוס אזי הנגזרת בעלת סימן קבוע (שלילי) והפתרון היחיד הוא אפס

שאלה

מישהו מוכן להסביר לי באילו מקרים כדאי לעשות גזירה איבר איבר, ומתי לעשות אינטגרציה איבר איבר? תודה.

כדאי? תמיד. מותר? כאשר יש התכנסות במ"ש לפי המשפטים שלמדתם בכיתה.

שאלות מעניינות

  • הוכח או הפרך:

תהי 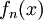f_n(x) סדרה של פונקציות גזירות ברציפות המתכנסות במ"ש לפוקציה f, אשר גם גזירה ברציפות,ב-[a,b]. אזי ש- f_n' \rightarrow f' במ"ש על הקטע [a,b].

  • בנוגע למשפט דיני לטורים, נניח שיש לי טור 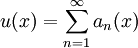u(x)=\sum_{n=1}^{\infty}a_n(x), כך ש-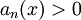a_n(x)>0 והטור מתכנס ב-I.

מתי אני יודע אם הפונקציה הגבולית רציפה, כך שאוכל להישתמש בדיני ולקבוע שההתכנסות במ"ש. נשמח לתשובה ממישהו,די דחוף! תודה!!! :)

תומר - אם ניקח את הסידרה cosnx ונחלק הכל ב n . האם קיבלת סידרה שמתכנסת במ"ש ? ומה עם נגזרותיה ? ... לגבי דיני - פשוט לבדוק רציפות לפי הגדרה - גם לא אמרת שהפונקציות בסידרה רציפות - שים לב לתנאי המשפט ! .

שאלה

שאלה שנתקעתי עליה ואשמח לכיוון:

int(arctan(x)/[(x*(ln(x+1))^2)], x = 0 .. infinity)

ניסיתי דיריכלה, חשבתי על השוואה, ופשוט לא מצאתי. אשמח לעזרה

מצטרף לשאלה!! איך פותרים את הדבר הזה?


(לא ארז/תומר) תנסה השוואה עם אחד חלקי [x*ln(x)^2]. שים לב ש arctanx שואף באינסוף לחצי פאי, ושעם קצת אלגברה אפשר להוכיח שמנת ה-ln-ים שואפת לאחד. כדי להראות התכנסות של האינטגרל החדש, אפשר להשתמש בהצבה t=ln(x), או לחילופין להשתמש במבחן האינטגרל+מבחן העיבוי לטורים

תודה רבה :)

זה לא נכון, כי יש בעיתיות גם בנקודה x=1 וגם באינסוף. ההשואה שנתת עוזרת רק לחלק של האינסוף

אבל אני לא חושב שאמורה להיות בעיה, כי זאת בעיה בנקודה, וזה לא אינטגרל לא אמיתי מסוג שני.
אתה מפצל את זה לשני אינטגרלים: האינטגרל מ-1 עד אינסוף מתכנס (כי מורידים את ה-ln בעזרת אי שוויון והאינטרגל (arctanx/x^2) מתכנס (השוואה עם 1/x^2)...
עכשיו בקשר לאינטגרל מ-0 עד 1 אתה יודע ש- ln(1+x)<x לכל x ב-[0,1] ולכן האינטרגל שלנו גדול מהאינטגרל של arctan(x)/x^4 וזה מתבדר ע"פ השוואה עם 1/x^4 שמתבדר בקטע [0,1], ולכן זה גדול מאינטגרל מתבדר וזה סה"כ מתבדר. (אשמח לקבל אישור מאחד המתרגלים =) ).
(לא ארז/תומר) עבור האינטגרל מ-0 עד 1, תנסה מבחן השוואה גבולי עם אחד חלקי x^2 . שים לב ש arctanx/x שואף לאחד וש ln(1+x)/x גם שואף לאחד כאשר x שואף לאפס.

ובקשר לזה שכתב מעלי- ה-x במכנה הוא לא בריבוע...

האמת שהאינטגרל המקורי היה בין 1 לאין סוף וזאת טעות שלי שכתבתי אפס, אבל זה באמת יהיה טוב לדעת מה קורה גם אם זה היה אפס.
תודה לשניכם :)

שאלות.

  • arctanx חיובי בקטע 1,infinity לא? היה תרגיל באחד המבחנים ששמו ערך מוחלט מסביב לarctan, באנטגרל שהתחום שלו הוא תהחום המצוין..
  • במבחן ההשוואה הגבולי. מותר לי להשוות פונק' חיובית עם פונק' שלילית, אם הגבול יוצא חיובי? לדוגמה, הפונקציה sinx חלקי x*lnx. בתחום [0.5,1], נניח ואני רוצה להשוות עם sinx חלקי x-1..
  • כאשר אני מפצלת אינטגרלים ל2 תחומים שונים [עם דגש על השונים!]. אם אחד מהם מתבדר, כל האינטגרל המקורי מתבדר, נכון? בלי קשר לחיוביות/שליליות של אחת הפונקציות..
  • בהמשך לשאלה שלמעלה - אם יש לי שאלה של 'לאילו ערכי אלפא', כאשר יש לי חיבור של 2 אינטגרלים - אחד ל"א מסוג ראשון והשני ל"א מסוג שני.. אז אם למשל עבור alpha>1 האינטגרל מסוג 1 מתבדר, אין מה לבדוק את האינטגרל השני גם?

וזהו, תודה רבה!

תשובה

  • כן הוא חיובי.
  • אם בתחום הפונקציה אי חיובית אז אם תכפלי אותה במינוס תקבל פונקציה אי שלילית. כמובן שמכפלה במינוס לא משנה התכנסות אינטגרל
  • נכון.
  • נכון
כן, אבל כשהפונק' הייתה שלילית, הגבול יצא לי חיובי. אם אני כופלת במינוס 1, הגבול יוצא שלילי..
לא יכול להיות שהגבול של המנה של שתי פונקציות אי שליליות יהיה שלילי
כעיקרון אני מדברת על הפונקציה sinx חלקי x*lnx. בתחום [0.5,1] אני משווה אותה עם sinx חלקי (1 פחות X). (יום יבוא ואני אלמד להשתמש בכתיב המתמטי של ויקיפדיה... מצטערת על הסרבול). בכל מקרה, שתי הפונקציות חיוביות בתחום הזה. אבל הגבול של המנה, כאשר X שואף ל1 מצד שמאל, הוא מינוס אחת..
כי ln שלילית בקטע הזה.
אוקי, אז בעצם מכפילים את הפונק' המקורית ב1- ואז מקבלים גבול חיובי, ואומרים שבגלל שהפונק' עם המינוס מתכנסת/מתבדרת ==> כך גם הפונק' המקורית?
נכון

שאלה

התכנסות במ"ש של ערך מוחלט של טור הפונק' גוררת התכנסות במ"ש של טור הפונק'?

כבר נשאל בעמוד זה. כן מכיוון שהשארית של טור קטנה או שווה לשארית של הטור בהחלט

שאלה

  • הסתבכתי,אפשר עזרה?
  • נניח שהפונקציה f מוגדרת ורציפה בקטע סגור x=a..b הוכח כי הסכום מאחד עד אינסוף של f^n מתכנס במ"ש בקטע זה אם ורק אם הסכום הנל(f^n) מתכנס נקודתית בקטע זה.


השאלה לא מנוסחת טוב. מה זה f ומה הוא קשור? מה ההבדל בין סכום מאחד עד אינסוף לבין טור?

תיקנתי... מה הבעייה בהגדרה של f פשוט פונקציה f(x)

שאלתי מה הקשר של f. גם g היא פונקציה אבל היא קשורה לשאלה בדיוק כמו f... האם היא פונקצית הגבול של הטור? האם הפונקציות בסדרה רציפות?
(לא ארז וגם לא תומר) בעצם הכיוון המעניין היחיד הוא מהתכנסות נקודתית לבמ"ש. אם f^n מתכנס נקודתית אפשר לראות כי לכל x נקבל f(x<1 (בערך מוחלט, הלוואי שזה לא היה קופץ כל הזמן). f רציפה לכן הערכים שהיא מקבלת מהווים קטע סגורc,d בתוך [-1,1), קטע בו הטור x^n מתכנס במ"ש. לכן כל סדרת נקודות אינסופית שתבחר בa,b עבור הטור לפי f שקולה בעצם לבחירת נקודות בc,d עבור הטור של x המתכנס שם במ"ש (ולפי מבחן הLIMSUP בעצם זה כל מה שצריך).


אבל למה f(x) בערך מוחלט קטן מ-1?

הסברתי במפורט בתשובה. לא בהכרח f<1 פשוט אם הוא מתכנס הוא קטן מאחד ולכן מתכנס במ"ש. אם הוא מתכנס במ"ש ברור שהוא מתכנס. זה כל מה שצריך להוכיח.

תשובה

אה.... התבלבלתי בין f_n לf^n.... מצטער.

הכותב מעליי צודק שהטור מתכנס כאשר 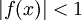|f(x)|<1, והוא מתכנס במ"ש כאשר 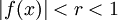|f(x)|<r<1 אבל בגלל שהפונקציה רציפה על קטע סגור ונניח מתכנסת בו אזי היא מקבלת מינימום ומקסימום ושניהם חייבים להיות קטנים ממש מאחד (אחרת היא לא הייתה מתכנסת בהם) ולכן התנאי מתקיים.


  • על מנת להוכיח שהוא מתכנס במ"ש בתנאי למעלה 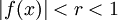|f(x)|<r<1 כל שצריך הוא מבחן הM

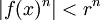|f(x)^n|<r^n.

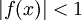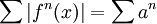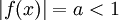  • על מנת להוכיח שהוא מתכנס עבור התנאי |f(x)|<1 כל מה שצריך הוא להסתכל נקודתית על הטור \sum |f^n(x)|=\sum a^n כאשר |f(x)|=a<1 וזה כמובן מתכנס.
  • טריוויאלי שהוא יתבדר בכל מקום אחר.
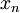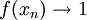  • על מנת להוכיח שהוא לא מתכנס במ"ש אם לפונקציה לא היה מקסימום אבל הsup שלה היה אחד: ניקח סדרה x_n כך ש f(x_n) \rightarrow 1 ולכן

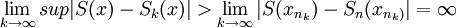
\lim_{k\rightarrow \infty} sup|S(x)-S_k(x)|>\lim_{k\rightarrow \infty} |S(x_{n_k})-S_n(x_{n_k)}| = \infty

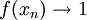(נבחר את n_k על מנת שההפרשים ישאפו לאינסוף. אנחנו יודעים שזה מותר כי f(x_n)\rightarrow 1)

שאלה

אם יש לי פונקציה ואני מפתח לה טור חזקות נניח עם רדיוס 1, איך אני מוודא לאחר הפיתוח שהפונקציה שווה לטור בקטע? וגם פה שאלה 4 כוון כללי אם אפשר...http://moodle.technion.ac.il/file.php/1098/Exams/2004-2005-spring-test-a.pdf

תשובה

הוא שווה לפונקציה רק ברדיוס ההתכנסות. מה הכוונה איך אתה מוודה? אם פתחת נכון זה חייב להיות שווה - הצעדים שלמדנו לפיתוח פונקציה לטור חזקות הם צעדים בהם השיוון בסוף חייב להתקיים (למשל פונקציה קדומה ששווה בנקודה אחת לטור החזקות [עדיף לבדוק את הנקודה אפס כמובן])


לגבי השאלה השנייה כבר שאלו אותה, תסתכל בארכיון 17

אבל אתה יודע שאם קיים טור חזקות המקדמים הם אלו של טיילור, למשל הפונקציה f(0)=0 f(x)=exp(-1/x^2) s היא שווה לטור החזקות רק באפס למרות שהטור מתכנס בכל הישר (הוא תמיד אפס כי כל הנגזרות באפס הן אפס) מה שאני שואל זה איך הייתי יודע להבחין שהם שווים רק באפס למרות שהטור מתכנס תמיד, רק שזה לא תמיד לערך הפונקציה?


אל תבלבל. הקטע עם הבדיקה בנקודה זה רק כאשר הוכחת שהפונקציה שלך היא קדומה של טור חזקות כלשהוא ועשית אינטגרציה איבר איבר. באופן כללי למדתם משפט אחד שמאפשר לכם להניח שטור החזקות עם מקדמי טיילור הוא אכן הפונקציה וזה כאשר הנגזרות חסומות (ראה את ההשלמה). במקרים אחרים (כמו זה שתארת) אסור סתם להניח שיהיה שיוויון.

כן, אבל בתכלס אם קיים טור חזקות המקדמים שווים למקדמי טיילור מה שאתה אומר זה להתייחס "כאילו" אנחנו לא יודעים את זה ולעבוד בשיטות אחרות כן? (במקרה והנגזרות לא בהכרח חסומות)

כן. יכול להיות שתשתמש בטריק כי אתה לא יודע להוכיח שהפונקציה שווה לטור חזקות, אבל גם יכול להיות שזה פשוט יהיה קל יותר מאשר לחשב את הנגזרות מכל סדר...

סבבה תודה רבה

שאלה

המבחן ב15:30 נכון? כמה זמן הוא יארך???

כן, שעתיים

שאלה

למה הסיגמה של 2*(n+1)*3^n חלקי שורש שלישי של n! מתכנס?

אתה מתכוון ל\sum \frac{2(n+1)3^n}{\sqrt[3]{n!}}? תקח את השורש הn-י ותקבל 3 חלקי אינסוף כלומר שואף לאפס (הרי \sqrt[n]{n!}\rightarrow \infty)

התכנסות אינטגרלים

האם האינטגרלים הבאים מתכנסים???

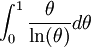  • \int_{0}^{1} \frac{\theta}{\ln(\theta)}d\theta.
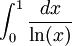
  • \int_0^1 \frac{dx}{\ln(x)}
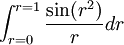  • \int_{r=0}^{r=1} \frac{\sin(r^2)}{r}dr.

האם אפשר לומר באינטגרל השלישי ש- 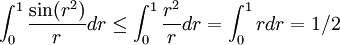\int_{0}^{1} \frac{\sin(r^2)}{r}dr \leq \int_{0}^{1} \frac{r^2}{r}dr = \int_0^1 rdr = 1/2, ואז עפ"י השוואה???


תשובה

לא לשכוח לבדוק אם האינטגרל הוא אמיתי בכלל או לא. למשל השלישי הוא פשוט בעל אי רציפות סליקה באפס ולכן אינטגרבילי (גם מה שרשמת נכון אבל בלי קשר)

בראשון ובשני הצד הבעייתי הינו 1. ניתן לבצע מבחן ההשוואה עם 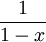\frac{1}{1-x}

שאלה

נתונה פונקציה f(x) בקטע [a,b] ונתון שהיא חסומה על ידי M.

צריך להוכיח שאם f אינטגרבילית זה גורר ש-f^2 אינטגרבילית.

חסימות זה לא בעיה, אבל הסתבכתי עם התנאי השני


אני יכול להשתמש במשפט שאם הפונקציות f,g אינטגרביליות בקטע כלשהו אז גם f כפול g אנטגרבילית שם, כאשר במקרה הזה g=f?

(לא ארז/תומר) ענו כבר על השאלה הזאת... לדעתי אי אפשר להשתמש במשפט, למרות שהוא נכון, כי אז התרגיל טריוויאלי.
הנה ההוכחה- יהי אפסילון גדול מאפס. בכל קטע g(x1)-g(x2)=(f(x1)+f(x2))*(f(x1)-f(x2)<2M*W כאשר W היא התנודה של f בקטע. (g מוגדרת כ f בריבוע). מאינטגרביליות f קיימות חלוקה עבורה סכום התנודות קטן מאפסילון חלקי 2M. ועבור אותה חלוקה בפונקציה g סכום התנודות יהיה קטן מאפסילון.

תומר - ומה עם מידת נקודות אי רציפות ? אם אתם יודעים שהפונקציה אינטגרבילית זה אומר שמידת קבוצת נקודות האי רציפות שלה היא אפס . מה עם נקודות האי רציפות של הפונקציה בריבוע ? האם היא מוכלת בזו של הפונקציה המקורית ? ואם כן מה זה אומר על מידתה ? ...

שאלה

צריך להוכיח שהטור הבא מתכנס במ"ש. f(x)= sum from 0 to infinity of (e^-nx)* cos(nx) s

בכל קטע (a, infinity] כאשר a>0

ניסיתי עם מבחן ה- m ולא הצלחתי. מישהו? אפשר להשוות עם e^-n במבחן הM לא?

(לא ארז/תומר) אני חושב שצריך להשוות עם e^-an ...

עם e^-n וזה עובד. עכשיו בסעיף הבא הם רוצים להוכיח/להפריך שf(x) שזה הסכום הוא פונקציה רציפה ב(o, infinity). הבעיה זה שזה קטע פתוח ולא סופי.. עדין אפשר להשתמש במשפט על טור של פונקציות רציפות המתכנס במ"ש?

תמיד משתמשים באותו טריק (לא התעמקתי בשאלה, מקווה שרלוונטי) אם ההתכנסות היא במ"ש על כל תת קטע סגור וסופי אז יוצא שפונקצית הגבול רציפה בכל נקודה בלי שתהיה התכנסות במ"ש על הקטע האינסופי/פתוח כולו.

תרגיל 11

מישהו יכול לכתוב שוב את הלינקים לתרגילים שבתרגיל 11, הלינקים לא עובדים לי. 

ארכיון 16...

שאלה

מתי יפורסמו ציוני התרגיל והבוחן (אני יודע שיש לנו אותם, הכוונה עם פקטור, וציוני תרגיל 8/10 אם אני לא טועה) והאחוזים מהציון הסופי?

מצטרף!!

תומר - יפורסם בשעות הקרובות . אני עצמי עוד בודק תרגילים שהוגשו באיחור(!) . סבלנות . 

יש חדש?

שאלה

אוקי, נניח ויש לי סדרת פונקציות, ואני צריכה לבדוק לאילו ערכי אלפא הסדרה מתכנסת במ"ש ב0,אינסוף (חצי סגור) וב[0,1]. קודם כל בדקתי את 0 אינסוף, והגעתי לזה שעבור אלפא קטן מ2 ==> הסדרה מתכנסת במש. התחום השני, [0,1], מוכל בתחום הראשון - ונניח שהגעתי לזה שהסדרה מתכנסת במש בתחום זה עבור אלפא גדול מ2-. מכיוון שהתחום מוכל, זה אומר לי גם שבפרט הסדרה מתכנסת במש גם עבור אלפא קטן מ2, וביחד - עם שתי המסקנות האלה - מתכנס לכל אלפא?


תשובה

לכאורה כן, אני לא מבין מה השאלה. הרי ברור שאם זה מתכנס במ"ש לכל אלפא גדול ממינוס 2 או קטן משתים בפרט זה מתכנס לכל אלפא. השאלה האמיתי היא אם החישובים שלך נכונים.

השאלה היא כזו - הוכחתי שעבור אלפא קטן מ2 זה מתכנס במ"ש ב0,infinity. רק רציתי לוודא שזה אומר שעבור אלפא קטן מ2 זה מתכנס במ"ש גם ב[0,1]. זה נכון?
הדגש הוא על הקטע הסגור? אם יש התכנסות באפס אז כן, אם לא אז לא
כן, מדובר על קטעים סגורים. תודה:)

אני טועה או שבהתחלת ההרצאה האחרונה רוני אמר שבטווח שבין רדיוס ההתכנסות לבין המינוס שלו(לא כולל הוא עצמו)- הפונקציה מתכנסת, ואח"כ הוא אמר שהיא גם מתכנסת במ"ש בכל קטע סגור שמוכל בקטע הזה.....?

זה נכון לגבי טור חזקות, אני לא בטוח איך זה קשור פה.
יש עוד מקום עם רדיוס התכנסות חוץ מטור חזקות??? ושאלתי כי זה נראה לי מוזר להוכיח משהו ואז להוכיח משהו ותר חזק במקום להוכיח ביחד. למה פה? איפה עוד אני יכול לכתוב???
לא פה בפורום, התכוונתי פה בשאלה הזו... רדיוס התכנסות זה מושג של טור חזקות, וכאן מדובר על סדרת פונקציות.

שאלה

מצטער על הבורות רגע לפני המבחן- מה זה גזירה איבר-איבר? ואינטגרציה איבר איבר? בבקשה שלא יהיה מסובך....

תשובה

נניח ויש לך טור מתכנס 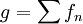g=\sum f_n. השאלה היא מהי הנגזרת של g. אם מותר לגזור איבר-איבר אזי 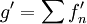g' = \sum f_n'. שים לב שזה לא תמיד נכון, רק כאשר המשפטים מאפשרים לגזור איבר-איבר.

אינטגרציה זה דומה 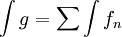\int g = \sum \int f_n

שאלה

אם טור חזקות מתכנס גם בR וגם בR-, זה אומר שהוא מתכנס במ"ש ב[0,R] וב[-R,0] ואז זה אומר שהוא מתכנס במ"ש ב[-R,R]?

תשובה

כן. באופן כללי אם טור מתכנס במ"ש בשני קטעים סגורים צמודים הוא מתכנס במ"ש באיחוד הקטעים. כי מהירות ההתכנסות עבור אפסילון היא המקסימום בין שני הn_0 של שני הקטעים.

:)

שיהיה בהצלחה לכולם! לא פחות מ100 :)

תומר - מצטרף ! שיהיה בהצלחה לכולכם - במבחן הזה ובכל אלו אחריו :)

תודה, ותודה לכם על סמסטר נפלא (עד כמה שהיה אפשר. אינפי, אתם יודעים). תודה על התרגולים המצויינים, אפילו שהיו יותר מידי אנשים בכיתה... ותודה על ההשקעה בנו ועל כל העזרה (האתר, וכל דבר אחר). אולי תהיו מתרגלים שלנו באינפי 3?
ושיהיה בהצלחה לכולם!

לארז ולתומר

רגע אחרי המבחן, וכמה ימים לפני שהאתר יתחיל לשמש, כנראה, תיכוניסטים תמימים שצעירים מאתנו בשנה, ואתם אורזים את הכל בשבילם, רציתי לומר לכם, לשניכם במ"ש, ת-ו-ד-ה ר-ב-ה!! על כל ההשקעה, הזמן, הרצון והכוח שהיה לכם להתמודד עם שתי קבוצות רועשות כמו שלנו, ועוד בקורס קשה כמו אינפי 2! שיהיה לכולנו המון בהצלחה בהמשך!


מצטרף בהחלט, המון תודה לשניכם, ואולי נתראה בהמשך...

מצטרפת.. ממש תודה על הכול! מה נעשה בלי Math-wiki..

מצטרף! זה לא מובן מאליו... ועם זאת, מתי נדע כמה פקטור יהיה(בטוח יהיה...!!)

תודה רבה על כל האיחולים - המתרגלים. (בלי קשר, אני אפרסם עוד כמה דקות פתרון למבחן בדף הקורס)


אני מסכים לגמרי עם כל השאר. אתם באמת השקעתם את כל כולכם בנו ובהצלחה שלנו. באמת רואים שאכפת לכם מאיתנו למרות כל הקיטורים, בקשות לדחיות, התחננויות ולפעמים אף בכי P= אני רק לא מבין משהו אחד. ניסיתי להבין מה הייתה התועלת בשיעורי חזרה ובתרגולים הנוספים שעשיתם, ואני לא מוצא בהם תועלת למבחן... לא עשינו אפילו תרגיל אחד שהיה אפילו דומה לשאלות שהיו במבחן (אני לא מתכוון לשאלות בדיוק כמו שהיו במבחן, אבל לפחות בסגנון ובנושאים)...  כאילו שמתם דגש בשאלות לא דומות למבחן בשביל מה? הרי ראיתם את המבחן כבר... לי אישית היה די קשה להגיע לבר אילן,לתירגולים, באותו היום אבל הגעתי בכל זאת כי חשוב לי להצליח במבחנים (כמו לכולנו), אבל בתכלס שאני מסתכל על היעילות שלהם לאחר המבחן לא עזר בכלל, אלא להיפך. כל מה שאני מנסה להגיד, זה שבתרגולי חזרה לפני מבחן, תעזרו קצת יותר בכך שתתרגלו אותנו נכון, ולא לבלבל לנו את השכל עם שאלות לא קשורות בכלל... אחר כך מתלוננים שאנחנו לא מקבלים ציונים נורמלים ואתם נאלצים לעשות פקטור סתם! תודה על הכול (וזה בשיא הכנות) כי באמת השקעתם בנו 

תשובה

אני אענה לשאלה שלך בשני מישורים

  • הראשון והחשוב יותר: מטרתנו הראשונה והעיקרית כמורים הינה ללמד אתכם מתמטיקה ולא להכין אתכם למבחן. הכנה למבחן הינה משנית (אמנם חשובה גם כן). קשה להגיע לבר אילן גם במהלך הסמסטר, אך אתם מגיעים על מנת ללמוד. הסיבה שאנו רואים את המבחן קודם לכן היא בעיקר על מנת לוודא איכות שלו (שאין טעויות, רמה סבירה וכדומה), עלינו להעביר שיעורי חזרה כאילו לא ראינו את המבחן.
  • שנית, אני אפריך לחלוטין את הטענות שהעלאת:
    • שיעור ההשלמה היה חלק מחומר הקורס וכלל שאלה שהופיעה כלשונה במבחן! (הוא היה לפני שראינו את המבחן). אז כבר 20 נקודות מתנה על שיעור ההשלמה והחומר שהועלאה לאתר (אני לא העברתי את השאלה פרונטלית אבל תומר כן). אמרנו לכם לקרוא את שיעור ההשלמה.
    • שיעור החזרה כלל שאלה כמעט זהה לחלוטין לשאלה 3 מהמבחן (אני העברתי אותה ותומר לא).
    • יום או יומיים לפני המבחן עניתי באתר על שאלה דומה לשאלה 2 במבחן, והדגשתי דברים שלא היו בשאלה המקורית כי ידעתי שזה יעזור למבחן.
    • שאר השאלות, בוודאי היו דומות והתעסקו בנושאים דומים...


מעבר לכך, תודה על ההכרה בעבודה שלנו. תאמינו לנו שמה שעכשיו נראה לכם לא כיף, בעתיד אתם תראו כאתגר שהצלחתם בו. החיים הם לא מיטת שושנים, ומי היה רוצה לישון במיטת שושנים בכלל? זה דוקר!

זה לא רק דוקר, זה גם צמיגי :P
מתי יעלו ציוני תרגיל?
אנחנו נעלה אותם היום

יש לי שאלה

האם בשאלה 4ב במבחן היה אפשר להגיד שההתכנסות היא ל0 כי תנאי הכרחי להתכנסות הטור היא שאיפת האיבר הכללי לאפס (הוכחה של התכנסות לאפס לא התכנסות במש)?

תשובה

כן, זה מוכיח בהחלט התכנסות נקודתית לאפס (ולא במ"ש כפי שציינת)

שאלה

למה מופיע לי ציון 0 בתרגיל מספר 2 אם הגשתי אותו? :S

זו שאלה פילוסופית?

הודעה

יש ציונים!!

מבחן

היה פקטור במבחן? ואם כן של כמה?

מצטרף לשאלה... מאוד חשוב לנו לדעת האם להגיש ערעור או שלא.... והאם לגשת למועד ב או לא בקיצור ממש חשוב לנו לעת האם היה פקטור...

תשאלו את המרצים, אנחנו (המתרגלים) לא יודעים.
מקור: https://math-wiki.com/index.php?title=אינפי_2_לתיכוניסטים_תש%22ע_-_שאלות_ותשובות&oldid=5877