הבדלים בין גרסאות בדף "לינארית 1 לתיכוניסטים תש"ע - שאלות ותשובות"
(←שאלה כללית) |
(←שאלה בקשר לשאלה והתשובה שנשאלו פה) |
||
| (477 גרסאות ביניים של 60 משתמשים אינן מוצגות) | |||
| שורה 12: | שורה 12: | ||
'''[[לינארית 1 לתיכוניסטים תשע - שאלות ותשובות - ארכיון 4| ארכיון 4]]''' - תרגיל 3 | '''[[לינארית 1 לתיכוניסטים תשע - שאלות ותשובות - ארכיון 4| ארכיון 4]]''' - תרגיל 3 | ||
| + | |||
| + | '''[[לינארית 1 לתיכוניסטים תשע - שאלות ותשובות - ארכיון 5| ארכיון 5]]''' - תרגיל 4 | ||
=שאלות= | =שאלות= | ||
| − | |||
| − | |||
| − | == | + | =שאלות= |
| − | + | ||
| − | + | ||
| − | == | + | == ציונים סופיים == |
| − | + | עוד מעט מתחיל סמס א', | |
| + | מתי יפורסמו הציונים הסופיים? | ||
| − | == | + | ==פגישה== |
| − | + | הפגישה היום (י"א תשרי) בקשר לרישום, היא עם הורים? | |
| + | |||
| + | עוד שאלה, באיזה שעה היא ואיפה? | ||
| + | |||
| + | ==שאלה בקשר לפתרון של מועד ב== | ||
| + | בשאלה 8 א כתבת ש (1,0) != (1,6) אבל אנחנו נמצאים בz3 אז זה לא אומר ש (1,6)=(1,0) ואז הטענה אינה נכונה? | ||
===תשובה=== | ===תשובה=== | ||
| − | + | נכון! בכלל לא שמתי לב לשאלה. מזל שאני לא נבחנתי על זה. אני אתקן ואעלה מחדש | |
| − | + | ||
| − | + | ==תרגילים נוספים?== | |
| + | שלום רב, | ||
| + | האם היו תרגולים נוספים אשר היינו אמורים להגיש (בחלקו העליון של דף זה נכתב: "הודעה חשובה !!! - יש להגיש את התרגילים הנוספים (13 , ו 14 כרשות למי שמגיש ) עד ,וכולל , 16.9.2010 ! למשל לתא הבודקת הילה הלוי בכר , או לתומר ביום רביעי או לניר ביום חמישי - בתרגולי החזרה . אנא הודיעו למי שאתם יודעים שלא יגיע לתרגולים אלו . תודה:):") או שזו טעות? תדה מראש. | ||
| + | |||
| + | ===תשובה=== | ||
| + | זה לא קשור לקורס הזה בשום צורה, הייתה טעות... פה יש 5 תרגילים בלבד | ||
| + | |||
| + | ==ציוני תרגיל== | ||
| + | הגשתי את תרגיל 4 ומופיע כאילו לא הגשתי אותו (מס' ת.ז. 205632516) | ||
| + | ==שאלה 1.ג במבחן== | ||
| + | האם כדי להוכיח סכום ישר, לא צריך להוכיח גם סכום ז"א ש- U+W=V. | ||
| + | |||
| + | ===תשובה=== | ||
| + | ברור שכן, שכחתי להוסיף את זה. אני אעלה עוד כמה דקות תוספת לפתרון. | ||
| + | |||
| + | :העלאתי את התוספת הדרושה. --[[משתמש:ארז שיינר|ארז שיינר]] 22:52, 13 בספטמבר 2010 (IST) | ||
| + | |||
| + | ==תרגילי בית== | ||
| + | היכן ניתן למצוא תרגילי בית שלא קיבלתי חזרה? | ||
| + | |||
| + | :לא ניתן למצוא אותם בשלב זה. | ||
| + | |||
| + | == בקשר לציוני התרגיל == | ||
| + | אנחנו נקבל את הציונים של תרגילים 4 ו5? | ||
| + | עברו כבר שבועיים והמבחן.. | ||
| + | |||
| + | אני צריך לדעת בשביל להחליט אם לעשות מועד ב'. | ||
| + | |||
| + | ===תשובה=== | ||
| + | הנה רשימת הציונים שיש בינתיים '''[[מדיה:10Linear1TargilTempGrade.pdf|ציוני תרגיל 1-4]]''' | ||
| + | |||
| + | ==בקשת הבהרה== | ||
| + | למה כוונתכם באמירה "הבוחן יהיה ציון מגן בלבד": | ||
| + | 1. אם הוא גבוה משיעורי הבית אז הוא יהיה במקומם. | ||
| + | 2. אם הוא גבוה מהמבחן אז החלוקה תהיה 80% מבחן, 10% בוחן, 10% שיעורים. | ||
| + | 3. אם הוא גבוה מהשיעורים אז החלוקה תהיה 80% מבחן, 10% בוחן, 10% שיעורים. | ||
| + | 4. אחר? | ||
| + | |||
| + | תודה, גל. | ||
| + | |||
| + | ===תשובה=== | ||
| + | מתוך ציון התרגיל בלבד הוא מגן. כלומר המבחן 80 אחוז בכל מקרה (אמנם זה כמו שרשמת, אבל רשמת רק אופציה אחת). | ||
| + | |||
| + | אם הוא גבוה משיעורי הבית זה יהיה 10 אחוז 10 אחוז, ואם נמוך זה יהיה 20 אחוז שיעורי בית. | ||
====תשובה לתשובה==== | ====תשובה לתשובה==== | ||
| − | תודה | + | תודה רבה על התשובה המהירה. |
| + | כרגע רשום באתר המידע האישי שהמבחן 85%, אני מניח שזה יתעדכן? | ||
| + | ומתי נקבל את ציוני תרגול 4-5 ואת השקלול הסופי של הציונים בתרגולים? | ||
| + | שוב תודה, גל. | ||
| − | + | :זה מוזר שרשום שם 85... או שזה יתעדכן או שזה ישאר ככה. אני לא חושב שזה הפרש משמעותי במיוחד. תקבלו את שאר הציונים כאשר אני אקבל אותם. | |
| − | + | ||
| − | + | ||
| − | ==שאלה | + | ==ציונים== |
| − | + | מתי יפרסמו את הציון הסופי או את הרכב הציון (אחוזים לכל דבר)? | |
| + | זה יכול להשפיע בהחלטה האם לגשת למועד ב'. | ||
| + | אשמח לתשובה מהירה. | ||
| + | ==שאלה== | ||
| + | :האתר לא פועל בחגים, ואני עוד לא ראיתי את הציון שלי, יש דרך כלשהי לראות את הציונים שלי? | ||
| + | :ועוד משהו, הציונים שעלו, הם רק בלינארית, או שזה גם בבדידה? תודה רבה, ושנה טובה לכולם! | ||
| + | ==ציון ביניים== | ||
| + | מה זה אומר בדיוק? וכמה עולה לצפות במחברות הבחינה? תודה. (אגב, ציוני הביניים עלו!!) | ||
| + | : ציון ביניים = חלקי הציון הכללי לפני מעבר שקלול. הציון הסופי יעלה רק לאחר שיעלו כל ציוני הביניים. | ||
| + | : עלות צפייה במחברת בחינה 5 ש"ח דרך כ"א. אפשר לצפות בה דרך האתר, אפשר גם להוריד אותה (ע"י לחיצה על כפתור השמירה תוך כדי הצפייה במחברת). (אינני מתרגל) | ||
| + | |||
| + | ==ציון מעבר== | ||
| + | הודיעו מתישהו מה הציון הכללי שצריך כדי לעבור? בכל מקרה, מה הציון? | ||
| + | :באופן כללי באוניברסיטה ציון מבחן עובר הוא 60 [[משתמש:ארז שיינר|ארז שיינר]] 21:44, 7 בספטמבר 2010 (IDT) | ||
| + | ::מה זה אומר שהציון עובר, או נכשל - במבחן? מה, אי אפשר לעבור את הקורס עם נכשל במבחן? | ||
| + | :::התכוונתי לציון סופי, לא ציון מבחן. ציון סופי 60 זה עובר (אחרי השקלול של ציון התרגיל). [[משתמש:ארז שיינר|ארז שיינר]] 23:10, 7 בספטמבר 2010 (IDT) | ||
| + | |||
| + | ==פקטור== | ||
| + | היה במבחן בלינארית פקטור? אם כן, כמה? | ||
| + | |||
| + | ==אחוזים== | ||
| + | בתחילת הסמסטר אמרו לנו שהציון מורכב מ: 80% מבחן, 10% בוחן, 10% ש.ב.. | ||
| + | רציתי לדעת האם יש שינוי בהרכב הציון? | ||
| + | |||
| + | :לא בטוח. אתם תראו את הציון הסופי כאשר הוא יופיע | ||
| + | |||
| + | ==תרגולים 4-5== | ||
| + | האם תעלו את הציונים שלהם בהמשך? תודה מראש. | ||
| + | :כן, כאשר הם יתקבלו | ||
| + | |||
| + | ==הערה== | ||
| + | קודם כל אני רוצה להגיד תודה על כל העזרה עם השאלות באלגברה לינארית. אני יודע שזאת בקשה גדולה ואתם לא חייבים להיענות לה, אך המתרגלים שעד עכשיו ענו על תשובות לאלגברה לינארית, יכולים לעזור גם בבדידה? כי נראה לי שאף אחד לא נכנס לדף של בדידה... תודה רבה!! | ||
| + | |||
| + | == פתרונות == | ||
| + | איפה מופיעים הפתרונות של המבחן??? | ||
| + | :'''[[מדיה: 10LinearTestASol.pdf|פתרון המבחן]]''' | ||
| + | |||
| + | ==ציונים== | ||
| + | איפה יופיעו הציונים? | ||
| + | :ומתי? | ||
| + | ::לפי מה שידוע לי - בעוד כשבוע. אבל אשמח לתשובה ממרצה/מתרגל. | ||
| + | |||
| + | ==תגובות לגבי פתרון המבחן== | ||
| + | תיקונים: | ||
| + | |||
| + | את שאלה 1 ו-4 לא עשיתי ככה שלא התייחסתי אליהם, | ||
| + | בשאלה 2, הצבת את 1 במקום a ועדיין השארת a בפיתרון הכללי.. (ובמטריצה) | ||
| + | בשאלות האמריקאיות- היה צריך להוכיח ולהפריך או רק לרשום כן/לא? | ||
| + | תוכל בבקשה להעלות את ההגדרות, כי יש כמה גרסאות ורציתי לדעת אם יש הבדל, למשל: | ||
| + | KerT= מרחב הפתרונות של המערכת Ax=0 כאשר A מטריצה מייצגת העתקה T, נקרא הגרעין של ההעתקה T. | ||
| + | (KerT) | ||
| + | / | ||
| + | מרחב הוקטורים שההעתקה T שולחת אותם ל-0. | ||
| + | סה"כ את שתיהן המרצה כתב לנו ושתיהן הגדרות פורמליות.. | ||
===תשובה=== | ===תשובה=== | ||
| − | |||
| − | == | + | צודק לגבי ההצבות, באמת טעות טפשית. |
| − | + | ||
| + | לא היה צריך להוכיח או להפריך, אבל אחת המטרות העיקריות של התשובות היא שמי שצריך יוכל ללמוד מהפתרון למועד ב'. (וכמובן גם מי שלא ייגש - טוב שיידע את התשובות הנכונות). | ||
| + | |||
| + | לגבי ההגדרות, אני לא יודע מה המרצים יקבלו. | ||
| + | |||
| + | ==מבחן== | ||
| + | בשאלה 3 ג' בתשובות, בשלב שלפני שמתקבלת המטריצה הסופית (כפל שתי מטריצות), במטריצה השמאלית, במקום <math>a_{n,n-1}</math>, אני חושבת שאמור להיות <math>-(n-1)</math> ולא <math>-n-1</math>. נכון? | ||
| + | |||
| + | :כן, תודה. | ||
| + | |||
| + | ==שאלה== | ||
| + | אם כתבתי בשאלה 2 ב' שאין בסיס וליד זה את האות פי, זה בסדר? כי אני יודע שהבסיס הוא פי, אבל כתבתי לפני זה שאין בסיס, תודה רבה | ||
| + | :(לא מתרגלת) פי? מה הקשר של פי לקבוצה ריקה? | ||
| + | :: הכוונה היא לאות <math>\ \empty</math>, המסמנת את הקבוצה הריקה. [[משתמש:עוזי ו.|עוזי ו.]] 22:01, 31 באוגוסט 2010 (IDT) | ||
| + | : תחליט: או שאין בסיס, או שיש בסיס והוא הקבוצה הריקה. האפשרות הראשונה בוודאי אינה נכונה, משום שלכל מרחב וקטורי יש בסיס (את המקרה הסופי הוכחתם בקורס; המקרה הכללי הוא משפט של Hammel). הקבוצה הריקה היא הבסיס (היחיד) של מרחב האפס. [[משתמש:עוזי ו.|עוזי ו.]] 22:01, 31 באוגוסט 2010 (IDT) | ||
| + | :: אני כתבתי שאין בסיס וליד זה את האות <math>\ \empty</math>, כל החישובים שלי בתרגים נכונים וגם על פי התשובות שלכם אין לי טעות אחת במבחן, הדבר היחיד שלא היה טוב זה שאחרי שהגעתי לזה שהחיתוך הוא 0 כתבתי שאין בסיס, וליד זה <math>\ \empty</math>, יורידו על זה הרבה נקודות? כי זה לא שהיה לי טעות אחרת חוץ מזה, וגם כתבתי <math>\ \empty</math> בפתרון הסופי, תודה | ||
| + | :::יורידו אולי נקודות, אני לא יודע מראש כמה. אם אין לך טעויות חוץ מזה יהיה לך ציון טוב. [[משתמש:ארז שיינר|ארז שיינר]] 12:09, 1 בספטמבר 2010 (IDT) | ||
| + | |||
| + | ==כמה שאלות לגבי פתרונות המבחן== | ||
| + | 1. בשאלה 3א האם אפשר היה להוכיח את היותה של הקבוצה בסיס על ידי שימוש בכך ש: | ||
| + | |||
| + | א. <math>|B|=N</math> ולכן משום היותה בסיס <math>dimV=n</math> ומשום <math>|C|=n</math> עפ"י הגדרתו אז <math>dimV=|C|</math>. | ||
| + | |||
| + | ב. בת"ל (וגם לא הוכחתי כפי שאתם הוכחתם אלא הוכחתי בשלילה, אמנם יצא לי יותר ארוך אבל אני מניח שזה בסדר, לא?!?). | ||
| + | |||
| + | 2. ב-3ב לא יותר קצר למצוא את המטריצה הנדרשת באותו אופן שאתם מצאתם את ההופכית שלה? | ||
| + | |||
| + | 3. בפתרון ל-2א יש לך טעות: הצבת a=1 וללכן לא יכול להיות שהפתרון הכללי למקרה של אינסוף פתרומנות תלוי ב-a. | ||
| + | |||
| + | 4. איך נעשית חלוקת הנקודות בין הסעיפים בין השאלות הפתוחות? לכל סעיף משקל שווה? | ||
| + | |||
| + | |||
| + | תודה מראש ושנה טובה! | ||
===תשובה=== | ===תשובה=== | ||
| − | |||
| + | 1. בת"ל ובגודל n + השלישי חינם זה סבבה. | ||
| − | + | 2. אפשרי, קצר זה עניין של דעה :) | |
| − | + | ||
| − | + | 3. כן, העירו לי על כך. תודה. כמובן שצריך להציב בכל מקום שם את a ולא רק בחלק מהמקומות :) | |
| − | + | 4. לא ידוע, יוחלט בעת הבדיקה. | |
| − | == | + | שנה טובה ומבורכת. |
| − | + | ||
| − | + | ==שאלה אחרונה== | |
| − | + | למה אם rankAB < min{rankA,rankB} אז A וגם B אינן הפיכות? תודה! | |
===תשובה=== | ===תשובה=== | ||
| − | + | כי אם A או B הפיכות, אז AB היא בעצם A או B שמבצעים עליה פעולות אלמנטריות, עשיית פעולות אלה לא משנות את מרחב השורות ובטח לא את מימדו, ואז המימד של מרחב השורות של AB היה שווה למימד המינימלי בין A ו-B ולא קטן ממש. | |
| + | :תודה רבה על התשובה בשעה מוקדמת! אשמח אם תוכל לענות לי על השאלה השניה לפני המבחן! תודה! | ||
| − | + | ==שאלה== | |
| + | במבחן 2003 מועד ב' שאלה 1 (צריך למצוא את [v]c, יש טעות בתשובה? עשיתי כמה פעמים מכל הכיוונים ויצא לי תשובה 4 ולא 2. תודה! | ||
| − | + | ==6.14 עמוד 62 בחוברת== | |
| + | בתשובות שבאתר הוספת לבסיס את (1,0,0). למה, לפי מה? | ||
| − | + | :מדרגים ומוסיפים את e_i עבור כל העמודות i של המשתנים החופשיים (כלומר משלימים איברים פותחים) | |
| − | + | ::אהה.. באמת? חידשת לי. תמיד כשרוצים להשלים קבוצה בת"ל לקבוצה פורשת אז שמים את הוקטורים מהקבוצה הבת"ל בשורות מטריצה, מדרגים, ורואים אילו משתנים חופשיים יש. לאחר מכן מוסיפים קבוצה ובה וקטורים <math>e_i</math>, עבור כל עמודה i שבה יש משתנים חופשיים? יש איזה משפט קשור או משהו שמסביר למה עושים דווקא ככה? תודה. | |
| − | + | ||
| + | :::זה פשוט מאד, כמו שאמרתי - משלימים את האיברים הפותחים. לאחר התוספת יש n איברים פותחים (אם יש n עמודות) ואז מרחב השורות הוא ממימד n ובהכרח מרחב השורות הוא כל F^n. | ||
| + | |||
| + | ==עזרה== | ||
| + | איך מוכיחים את המשפט: יהי בסיס v1,..,vn לV וקבוצה w1,..wn בW, אז יש העתקה לינארית כך ש T(vi(=Wi? תודה! | ||
===תשובה=== | ===תשובה=== | ||
| − | + | לא יודע איך הוכיחו לכם בכיתה (כנראה אחרת) אבל אפשר עם המטריצה המייצגת. כלומר למצוא את המטריצה המייצגת לפי ההגדרה נקרא לה A ואז ההעתקה Tx=Ax היא העתקה לינארית שמקיימת את הדרישה. | |
| + | :המטריצה המייצגת '''הוגדרה''' בהתבסס על המשפט הזה ולכן אני לא חושב שמותר להשתמש בה (אני לא מתרגל). | ||
| − | == | + | ==שיחלוף== |
| − | + | במשוואה שכוללת מטריצות, מותר לשחלף את שני האגפים וזה ישמור על שיוויון, בלי להסביר או להוכיח (אם זה לא התרגיל), נכון? | |
| + | :אתה מתכוון ש-<math>A=B\iff A^T=B^T</math>? בטח שזה נכון. זו בדיוק אותה מטריצה, ופעולת השיחלוף מוגדרת היטב (חד-ערכית). אני לא מתרגל, אבל אני כמעט בטוח שלא צריך להסביר או להוכיח. | ||
| + | |||
| + | ==העתקת המטריצה== | ||
| + | בחוברת עמוד 52 שאלה 1.10 ב' - או שלא הבנתי את ההגדרה, או שיש טעות בהגדרת הטווח של ההעתקות T,S. למשל עבור העתקה T: הרי כפל של מטריצה מסדר m על n בוקטור מסדר n על 1 נותן וקטור מסדר m על 1 ולא הפוך! | ||
| + | |||
| + | |||
| + | ועוד דבר - צריך לזכור בעל פה את ההגדרות של העתקת המטריצה, ההעתקות <math>L_A</math>, <math>T_A</math> ועוד? אם לא, אז אילו הגדרות של העתקות כן צריך לזכור בעל פה? | ||
===תשובה=== | ===תשובה=== | ||
| − | + | אתה צודק זה באמת צריך להיות הפוך. | |
| − | + | לא בטוח למה אתה מתכוון, אלה דברים שלמדתם בהרצאה, תלוי מה המרצה אמר שצריך לזכור. | |
| − | + | ==מושג== | |
| + | מה זה "מרחב האפס"? | ||
| + | :קבוצה שהאיבר היחיד בה הוא 0, והקבוצה הזאת היא מרחב וקטורי כל התנאים של מרחב וקטורי מתקיימים. | ||
| + | ::תודה. בעמוד 50 שאלה 11.15 ד' (בחוברת), אומרים "מצא בסיס למרחב האפס של A". מה הכוונה? | ||
| + | :::<s>הכוונה היא שתמצא בסיס למרחב <math>\{\vec0_A\}</math>, כלומר המרחב שכולל את האיבר הנייטרלי לחיבור ב-A.</s> | ||
| − | == | + | ===תשובה=== |
| − | + | מרחב האפס בלי הקשר הוא אכן המרחב שמכיל בלבד את אפס. מרחב האפס של מטריצה, בד"כ, הוא מרחב הפתרונות של המערכת ההומוגנית. | |
| − | + | :תודה! | |
| − | ==שאלה | + | ==שאלה 8 ממבחן 2002 מועד א'== |
| − | + | למה סכום איברי המטריצה הוא 1?? מאיפה בתשובות הוא הביא את התשיעית הזאת? המטריצה P היא <math>(0,2,1),(1,0,2),(2,1,0)</math> ולכן סכום איברי המטריצה הוא 0+2+1+1+0+2+2+1+0=9, למה 1?? תודה! | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | אתה רשמת את מטריצת המעבר מB לC. אבל P היא ההופכית שלה, מטריצת המעבר מC לB. | |
| + | :וואלה, תודה.. | ||
| − | + | ==החוברת עמוד 48== | |
| + | כתוב שם שמרחב העמודות הוא תת מרחב של <math>F^n</math> כאשר <math>A</math> מסדר <math>mxn</math> ואני חושבת שמרחב העמודות הוא תת מרחב של <math>F^m</math>. לא? (כנ"ל לגבי מרחב השורות, רק הפוך) | ||
| − | : | + | :נכון זו טעות בחוברת. |
| − | + | ==שאלה 8 ממבחן 2002 מועד א'== | |
| + | איך ניגשים לשאלה כזאת? מה הקשר בין הפיכות של הפונקציה לRANK שלה? אפשר הסבר מפורט בבקשה? זה ממש מבלבל! וגם, למה נתונה מטריצה B אם היא נמצאת בשאלה בכלל? תודה רבה מראש | ||
| − | == | + | ===תשובה=== |
| − | + | יש כמה קשרים בין השניים. למשל הrank של מטריצה ריבועית מגודל n שווה לn אם"ם היא הפיכה. אם נסתכל על זה בתור העתקות ליאריות, אז הrank הוא מימד התמונה והוא קטן ככל שמימד הגרעין גדל. | |
| + | :'''למה אני אמור להסיק שA אינה הפיכה ב3?''' | ||
| + | ::אם תסתכל על המשפט שרשמתי אז תראה שA הפיכה אם"ם הrank שלה הוא n אם הrank של A^2 קטן מהrank של A בוודאי הוא קטן מn ולא יכול להיות שהיא הפיכה. אבל אם A הפיכה בוודאי A^2 הייתה צריכה להיות הפיכה. | ||
| + | |||
| + | ==שאלה 1 מקובץ מצורף תרגול 4== | ||
| + | שלום רב. בשאלה התבקשנו להוכיח ש- <math>[I]_C^B</math> הפיכה. האם לא מספיק פשוט לומר ש- <math>([I]_C^B)^{-1}=[I]_B^C</math> ע"י בדיקה שאכן מתקיים שמכפלתן משני הצדדים היא <math>I</math> תודה, גל. | ||
===תשובה=== | ===תשובה=== | ||
| − | + | אפשר, אם ידוע המשפט שקיימת מטריצת מעבר בין כל שני בסיסים ואז להשתמש בנוסחא של מטריצת מעבר. | |
| − | : | + | :כלומר ש'''אם''' מבקשים ממני במהלך המבחן להוכיח את זה אסור לי להשתמש במה שאמרתי? |
| − | :: | + | ::תלוי מה יבקשו ספציפי. אם השאלה הייתה מופיעה כמו שהיא במבחן זה היה בסדר. תשאל בזמן המבחן. |
| − | + | ||
| − | + | ==שאלה== | |
| + | אם v מוכל בw וגם dim של v שווה לdim של w אזי v=w זה משפט? וכיצד ניתן להוכיח? | ||
| − | == | + | ===תשובה=== |
| + | שאלה 7.7 תרגיל 4. | ||
| − | + | ===לא ענית לי על שתי השאלות: זה משפט? איך מוכיחים?=== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | זה עובדה, ומוכיחים כמו בפתרונות שיש באתר כמובן. | |
| − | + | ||
| − | + | אפשר להשתמש בזה אלא אם צריך להוכיח את זה במפורש. | |
| − | + | ||
| − | + | ==mod== | |
| + | המספר -1 בZ5 כלומר <math>-1 mod 5</math> זה 1 או 4? תודה! | ||
| − | + | ===תשובה=== | |
| + | <math>-1 = 4 +(-1)\cdot 5</math> ולכן זה 4. | ||
| + | ==שאלה== | ||
| + | למה אם למערכת הומוגנית Ax=0 יש פתרון יחיד, אזי A הפיכה? תודה! | ||
===תשובה=== | ===תשובה=== | ||
| − | + | קודם כל זה נכון רק אם '''A ריבועית'''. יש כמה וכמה הוכחות, למשל מטריצה ריבועית שקולת שורה למטריצת היחידה אם"ם היא הפיכה, ואם הצורה הקנונית של מטריצה ריבועית היא לא מטריצת היחידה סימן שיש לה משתנים חופשיים ולכן יותר מפתרון אחד. | |
| − | יותר | + | דרך אחרת להסתכל על זה היא שעמודות A בת"ל אם"ם למערכת Ax=0 יש פתרון יחיד, וידוע שעמודות מטריצה ריבועית בת"ל אם"ם היא הפיכה. |
| + | :תודה! | ||
| + | |||
| + | ==פרטים על המבחן בעמוד הראשי== | ||
| + | פרטים על המבחן בעמוד הראשי | ||
| + | :מה לגבי כמה זמן המבחן ומה המבנה שלו? | ||
| + | ::כבר אמרו את זה בהרצאות. | ||
| + | :::ומי שלא הקשיב או לא היה מרוכז? או לא היה בשיעור? | ||
| + | ::::שישאל את החברים שלו. שאלות לגבי המבחן צריכות להיות מופנות למרצים ולא למתרגלים. | ||
| + | |||
| + | ===שאלה קטנה=== | ||
| + | איפה זה בניין 507? זה הבניין שאנחנו בדרך כלל לומדים בו או בניין אחר? תודה! | ||
| + | :אנחנו לומדים ב-604. | ||
| + | ::אז אפשר הכוונה לגבי איפה זה 507? | ||
| + | :::507 זה הבניין הגדול עם המבנה המיוחד והמגני דויד למעלה, ממש ליד הבניין שאתם לומדים בו. | ||
| + | |||
| + | ==שאלה/בקשה== | ||
| + | נכון יש משפט שאומר (אני לא יודע ממש איך לכתוב בשפה המתמטית בפורום, לכן הבינו ש2 אותיות אחרי הT פירושן שהאות הראשונה למעלה מימין והשנייה למטה מימין וכו'): <math>[T]FG=[Iw]HG[T]EH[Iv]FE</math>? אז השאלה שלי היא, למה צריך את המשפט הזה תכלס? מתי המשפט הזה עוזר? והאם מתרגל יכול, בבקשה, להביא תרגיל אחד שבו חייבים/ רצוי מאוד להשתמש במשפט הזה? תודה רבה! | ||
| + | |||
| + | ===תשובה=== | ||
| + | <math>[T]_G^F=[Iw]_G^H[T]_H^E[Iv]_E^F</math> | ||
| + | |||
| + | השתמשנו בנוסחא הזו בשאלה הקודמת שלך... פשוט שם הייתה גם המטריצה <math>[I]_S^S</math> שהיא שווה למטריצת היחידה ולכן לא הזכרנו אותה. | ||
| + | |||
| + | == שאלה == | ||
| + | מבחן 2004 מועד א' שאלה אמריקאית 3.. איך מוצאים את המימדים של U ו W? | ||
| + | :(אני לא מתרגל)- 2 הSPANים פורשים, רק תבדוק אם יש בכל אחד מהSPANים איברים שתלויים אחד בשני, אם יש- תוריד אותם, ותישאר עם בסיסים לU וW. | ||
| + | |||
| + | ===תשובה=== | ||
| + | מעבירים לצורה וקטורית שמים בשורות מטריצה ומדרגים. | ||
| + | |||
| + | ==מבחן תשס"ד מועד ב' חלק אמריקאי שאלה 2== | ||
| + | התשובה לא אמורה להיות A^-1*B במקום B*A^-1? כי <math>[T]AB=[I]SB*[T]AS=(A^-1)*B</math> לא? תודה! | ||
| + | |||
| + | ===תשובה=== | ||
| + | לא נתון שB הוא בסיס בכלל. [T] צריכה לקיים את המשוואה <math>[T][v]=[Tv]</math>. לכן <math>[T][v_i]=[T]v_i=[Tv_i]=w_i</math> (כי הקואורדינטות לפי הבסיס הסטנדרטי שוות לוקטור עצמו). אבל <math>A^{-1}v_i=e_i</math> ואז <math>BA^{-1}v_i=Be_i=C_i(B)=w_i</math> כפי שרצינו. | ||
| + | |||
| + | |||
| + | דרך אחרת להוכיח: (פשוט הרבה יותר) | ||
| + | |||
| + | <math>[T]=[T]_S^S=[T]_S^A\cdot [I]_A^S=BA^{-1}</math> | ||
| + | |||
| + | ==שאלה על הוכחה== | ||
| + | האם ההוכחה הזאת קבילה?: נתון ש<math>AB=I</math> וכי <math>T:F^{n\times{n}}\rightarrow{F^{n\times{n}}}</math> כך ש:<math>T(X)=BX</math>, אני צריך להוכיח ש<math>T</math> על: | ||
| + | "נניח -T לא על: לכן קיים <math>Q\in{F^{n\times{n}}}</math> כך שלכל <math>Z\in{F^{n\times{n}}}</math> | ||
| + | <math>T(Z)\not=Q</math> לכן <math>BZ\not=Q</math> לכן <math>ABZ\not=AQ</math> כלומר- <math>Z\not=AQ</math> בסטירה לכך שהטענה נכונה עבור כל <math>Z\in{F^{n\times{n}}}</math> לכן T על? האם זה נכון? | ||
| + | |||
| + | ===תשובה=== | ||
| + | כן, עדיף הוכחות כאלה לבצע בחיוב ולא בשלילה. תהי Q מטריצה כלשהיא, אזי המקור שלה הוא AQ ולהוכיח את זה. | ||
| + | כן אבל בתרגיל הספציפי הזה אסור היה להשתמש במשפט ש<math>AB=BA=I</math> היה נתון רק ש<math>AB=I</math> | ||
| + | |||
| + | == שאלה== | ||
| + | מבחן 2 שאלה אמריקאית 2.. | ||
| + | הטענה חייבת להיות לכל Im(z)==0 אחרת זה לא יכול להתקיים | ||
| + | : מה זה מבחן 2? איזו שנה? איזה מועד? | ||
| + | ::2005 מועד א' | ||
| + | :::נראה לי שאתה צודק... יהי <math>z=x+yi</math> ולכן <math>z^3=x^3+3x^2yi-3xy^2-y^3i=x^3-3x^2yi+3xy^2+y^3i=(x-yi)^3</math> נפשט ונקבל ש- <math>6x^2yi-6xy^2-2y^3i=-6xy^2+(6x^2y-2y^3)i=0</math>. לאחר השוואה אני קיבלתי שאמנם ישנם אינסוף מקרים אבל בכולם <math>y=0=Im(z)</math> | ||
| + | |||
| + | ===תשובה=== | ||
| + | [[#שאלה ממבחן 2005 מועד א]] | ||
| + | |||
| + | ==מטריצות סימטריות ואנטי סימצטריות== | ||
| + | שאלה: אם <math>A</math> ו-<math>B</math> סימטריות (שתיהן ריבועיות מאותו גודל) אז: האם <math>ABA</math> סימטרית? | ||
| + | חשבתי על לפתור בדרך הזו: לפי סימטריות מתקיים ש: <math>A=A^t</math> וגם <math>B=B^t</math> ולכן <math>ABA=A^tB^tA^t=(BA)^tA^t=(A(BA))^t=(ABA)^t</math>. אי לכך גם <math>ABA</math> סימטרית. עם זאת, במבחן של 2003 (מועד א), זוהי שאלה 8 בחלק של האמריקאיות. אם מה שאני אומר נכון הרי שהתשובה אמורה להיות 3, אבל באתר כתוב שהתשובה היא 1. מה הטעות שלי? תודה, גל. | ||
| + | |||
| + | |||
| + | ===תשובה=== | ||
| + | אתה צודק, ABA סימטרית אם A,B סימטריות מאותו גודל | ||
| + | |||
| + | ==מבחן תשס"ד מועד א' חלק אמריקאי שאלה 11== | ||
| + | איך פותרים שאלה כזאת? הצלחתי להבין ש | ||
| + | <math>[T]B=(u1,u2,u3;0,0,0;w1,w2,w3)</math> (; מפריד בין עמודות) | ||
| + | אבל איך יודעים איפה יש עוד אפסים? אם התשובה היא 2 או 4? תודה רבה! | ||
| + | ===תשובה=== | ||
| + | אני לא מתרגל אבל נראה לי שאני יכול לרמוז לך- תסתכל על הבסיס של האימג'- כל איבר בתמונה אתה יכול להציד כצירוף ליניארי שלהם. | ||
| + | :לא הייתי עולה זה בחיים, אבל הבנתי- תודה רבה! | ||
| + | |||
| + | ==מבחן תשס"ד מועד א' חלק אמריקאי שאלה 9== | ||
| + | למה התשובה הנכונה היא- כל התשובות לא נכונות? אני זוכר שלמדנו משפטון שאומר שאם v1,..vk בת"ל אזי Tv1,..Tvk בתל כלומר 3 היא התשובה הנכונה.. לא? תודה! | ||
| + | |||
| + | ===תשובה=== | ||
| + | המשפטון שאתה מזכיר מחייב T '''חח"ע'''. למשל העתקת האפס תהווה דוגמא נגדית לסעיף זה | ||
| + | |||
| + | ==מבחן תשס"ד מועד א' חלק אמריקאי שאלה 4== | ||
| + | הצלחתי להבין, בשיטת האלימנציה, שהתשובה היא T32=0, אבל אני ממש לא יודע בדיוק למה, אפשר בבקשה הסבר קצר על למה אפשר לדעת בוודאות שT32=0 ואיך אפשר להוכיח את זה? תודה! | ||
| + | |||
| + | |||
| + | ===תשובה=== | ||
| + | נבנה בסיס לגרעין של ההעתקה. הגרעין של T^2 בהכרח '''גדול ממש''' מהגרעין של T אחרת ההעתקה תתקע על אותו מצב ולא תתאפס בחיים (אבל נתון שהיא מתאפסת). ולכן מימד הגרעין גדול ב1 לפחות. אחרי 32 צעדים כאלה נגיע לגרעין בגודל 32 - כלומר העתקת האפס. | ||
| + | |||
| + | מדוע ההעתקה תתקע? אני אשאיר את זה כתרגיל. | ||
| + | :למה גרעין בגודל 32 הוא העתקת האפס? כי המימד הוא 32? | ||
| + | :וזה נכון לומר שהגרעין של TT חייב להיות גדול ממש מהגרעין שלT כי אם היה להם אותו מספר של איברים בגרעין אז מה שמאפס את T^1024 מאפס גם את T^1023 ואז זה אומר ש T^1023 הוא העתקת האפס, וככה עד שמגיעים ל-שT היא העתקת האפס תמיד, אבל יודעים שהיא לא העתקת האפס תמיד? תודה | ||
| + | |||
| + | ::קודם כל כן, אם הגרעין בגודל 32 אז הוא כל המרחב ולכן זו העתקת האפס. | ||
| + | |||
| + | ::שנית, לא זו לא הוכחה נכונה. צריך להוכיח שאם נשלים את הבסיס של הגרעין של T^n לבסיס למרחב כולו, אזי הוקטורים שהשלמנו מהווים גם בסיס לתמונה של T^{n+1} ואז ברור שההעתקה חוזרת על עצמה. לא בטוח שזו הוכחה כל כך פשוטה. | ||
| + | |||
| + | ==מבחן תשס"ד מועד א' חלק אמריקאי שאלה 1== | ||
| + | כל מה שאני יודע הוא שהאפסיות של T היא לפחות 1 כי בטוח שV שהוא לא וקטור האפס נמצא בגרעין, וגם ש TT=0 ולכן לכל u מתקיים T(Tu)=0 ולכן התמונה מוכלת בגרעין ולכן dim(ImT)<=dim(KerT). אבל כל מה שזה נותן לי זה שהמימד של V הוא לא אפס! אפשר עזרה? תודה רבה! | ||
| + | ===תשובה=== | ||
| + | המימד הוא בטוח לא 4 כי 4 זה המימד של כל ההעתקות הלינאריות, והקבוצה הזו לא מכילה את כולם. המימד הוא גם לא אפס, יש יש העתקות שונות מאפס כאלה. | ||
| + | |||
| + | נותר לבחור בין 1 לבין 2. נשלים את v לבסיס בעזרת u. אם ההעתקה שונה מאפס, u חייב להשלח לסקלר כפול v (אחרת פעם שנייה שנפעיל את ההעתקה היא לא תתאפס, ישאר שם גורם עם u.) לכן כל שתי העתקות יהיו ת"ל על ידי איפוס הסקלר הזה, ולכן המימד הוא אחד. | ||
| + | :תודה רבה, רק עוד שאלה קטנה, איך יודעים שהמימד של כל ההעתקות הוא 4? תודה! | ||
| + | |||
| + | ::זה משפט שיש איזומורפיזם בין מרחב ההעתקות למרחב המטריצות. ואנחנו יודעים מהו המימד של מרחב המטריצות 2 על 2 | ||
| + | :::הבנתי, תודה! | ||
| + | |||
| + | ==שאלה על מכפלת מטריצת הפיכה והשחלוף שלה== | ||
| + | טענה: עבור <math>A</math> הפיכה הרי שיתקיים ש- <math>A^t</math> הפיכה (עפ"י משפט) ולכן <math>A^tA</math> הפיכה כי מכפלת שתי מטריצות הפיכות תתן מטריצה הפיכה נוספת. | ||
| + | השאלה שלי האם זה הסבר מספק לקיום טענה זו. אם לא, מה עליי להוסיף? | ||
| + | ובלי קשר, האם עליי להוסיף הערה מדוע המכפלה <math>A^tA</math> מוגדרת או שזה ברור? | ||
| + | תודה, גל. | ||
| + | |||
| + | |||
| + | :בגדול זה בסדר, תלוי מה אתה נדרש להוכיח. בזמן מבחן שואלים את המרצה אם צריך להוכיח כך וכך. | ||
| + | |||
| + | :: אוקי תודה. האם יהיו מתרגלים או מרצים כלשהם במבחן (אלי אמר שהוא לא יהיה)? אם כן, איך זה הולך? אתם נכנסים לשאלות או שחייבים לשאול לפני הבחינה? | ||
| + | |||
| + | :::יהיה מי שיענה על שאלות בזמן המבחן (על שאלון המבחן ולא רמזים לפתרון כמובן) | ||
| + | |||
| + | == קישורים למבחנים == | ||
| + | כשעשיתם עריכה לדף של לינארית הוצאתם את הקישורים למבחנים לדוגמא אפשר להחזיר אותם? תודה(: | ||
| + | :זה נמצא ב[http://www.math-wiki.com/index.php?title=%D7%A2%D7%9E%D7%95%D7%93_%D7%A8%D7%90%D7%A9%D7%99&oldid=5475 היסטורית הדף]. | ||
| + | |||
| + | |||
| + | ::הם פשוט הועברו בטעות לבדידה במקום ללינארית. הם הוחזרו למקום בדף של לינארית | ||
| + | |||
| + | ==שאלה== | ||
| + | האם נושא הדטרמיננטות כלול בחומר למבחן? | ||
| + | |||
| + | אני לא מתרגל, אבל ודאי שלא | ||
| + | |||
| + | ==שאלה דחופה== | ||
| + | מחר צריך לבוא בזמן של ההרצאה (9) או בזמן של התרגול (13:00)? תודה רבה! | ||
| + | |||
| + | :לא יודע מתי המרצים יגיעו. המתרגלים בגדול אמורים לבוא בזמן התרגול הרגיל. | ||
| + | |||
| + | :לפי מה שידוע לי אצלנו (אלי) מתחילים ב-0900. | ||
| + | |||
| + | מי שלומד עם אפי מתי צריך להגיע?? | ||
| + | לפי מה שזכור לי הוא אמר שהוא לא יבוא.. אנחנו צריכים לבוא ב9 או ב1? | ||
| + | ::אז כנראה שמי שלומד עם אפי צריך להגיע ב1, כי שיעור החזרה שלנו היה ביום שישי, ומחר יהיה לנו רק שיעור חזרה עם המתרגלים ב1.. | ||
| + | |||
| + | ==חח"ע ועל של ה"ל== | ||
| + | שלום רב, | ||
| + | נניח ונתונה לי ה"ל <math>T:V->V</math>. האם נכון לומר ש <math>T</math> חח"ע אם"ם <math>T</math> על? ואם כן, האם עליי להסביר במבחן מדוע? | ||
| + | |||
| + | תודה, גל. | ||
| + | |||
| + | ===תשובה=== | ||
| + | זה נכון ונובע ממשפט הדרגה V=dimKer+dimIm (צריך לצטט את המשפט ולהסביר למה זה נובע) | ||
| + | |||
| + | למעשה הטענה היא יותר כללית. תהי T:V->W כך שהמימדים של V,W שווים, אזי T על אם"ם T חח"ע. | ||
| + | |||
| + | ==2.15ב'== | ||
| + | אם אני רוצה למצוא את kerTa אז מה שצריך לעשות זה לכפול את המטריצה A במטריצה כללית מסדר 2x2 ולהשוות לאפס- ואז למצוא את המטריצה הכללית?- הכוונה במטריצה כללית זה שאני אסמן a b c d במקום קבועים במטריצה ואז אבדוק מה אני אקבל.. וזה יהיה הker? | ||
| + | |||
| + | :כן, הגרעין זה מה שנשלח לאפס על ידי ההעתקה. | ||
| + | |||
| + | ==שאלה== | ||
| + | אם אני יודע ש:<math>\dim (W+U)= \dim W + \dim U</math> וגם <math>\dim V= \dim W + \dim U</math> | ||
| + | כאשר<math>U,W\le V</math> אז אני יכול להגיד ש:<math>U\oplus W=V</math> ? | ||
| + | |||
| + | ===תשובה=== | ||
| + | כן | ||
| + | |||
| + | :(לא אני שאלתי את השאלה) למה כן? אם למשל <math>U=\{(a,0,0)\}</math>, <math>W=\{(0,a,0)\}</math>, <math>V=\{(a,0,b)\}</math>? (כך ש-a,b שייכים ל-R) | ||
| + | :ומה ז"א: <math>U,W\le V</math>? | ||
| + | ::אתה צודק, זה לא נכון (לא אני רשמתי את התשובה הקודמת). אם נוסיף את התנאי ש-<math>U+W=V</math> זה כן יהיה נכון. <math>U,W\le V</math> משמעו <math>U,W</math> תת מרחבים של V. | ||
| + | |||
| + | ===תשובת מתרגל=== | ||
| + | המשפט נכון, והרי הוכחה: | ||
| + | |||
| + | נתון U,W תתי מרחב של V. אזי ברור ש<math>U+W\subseteq V</math>. לכן לפי הנתון <math>dim(W+U)=dimV</math> יש לנו תת מרחב עם מימד שווה למרחב ולכן הם שווים <math>U+W=V</math>. | ||
| + | |||
| + | כעת לפי משפט המימדים <math>dim(U+W)=dimU+dimW + dim(U\cap W)</math> ולכן לפי הנתון <math>dim(U\cap W)=0</math> ולכן <math>U \cap W = \{0\}</math>. | ||
| + | |||
| + | וזה מה שצריך על מנת להוכיח סכום ישר. | ||
| + | |||
| + | תודה רבה! ואגב לזה שהביא את הדוגמה, בדוגמה שלך W לא תת מרחב של V. | ||
| + | אפשר להשתמש בזה או שצריך להוכיח? | ||
| + | :נכון, זה בגלל שלא הבנתי מה אומר סימן ה"קטן-שווה". מצטרפת לשאלה. | ||
| + | ::צריך להוכיח. | ||
| + | |||
| + | ==char-ים במבחן== | ||
| + | כמעט לא התעסקנו ב-char-ים בשיעורים, לא תרגלנו והמרצים/מתרגלים בד"כ הזכירו את זה כהערת אגב. יהיו char-ים במבחן? תודה, 16:11, 28 באוגוסט 2010 (IDT) | ||
| + | |||
| + | ===תשובה=== | ||
| + | לא יהיה מעבר לדברים דומים למה שעשינו בכיתה. | ||
| + | |||
| + | ==1.28== | ||
| + | לא הבנתי את התרגיל בכלל. את <math>T(f)</math> אמנם מצאתי בלי בעיה, אבל איך מוצאים את <math>T^{-1}(f)</math>? קראתי פה שאלה ותשובה: | ||
| + | |||
| + | '''''איך אני מחשב את ההעתקה ההפיכה?''''' | ||
| + | '''יש כמה דרכים. אחת מהן למדתם בהרצאה- בעזרת ההופכית של המטריצה המייצגת. הדרך השנייה היא לפי משפט ההגדרה - מספיק לבחור בסיס בתמונה ולראות מה המקור שלו וכך אפשר לחשב את המטריצה המייצגת של ההעתקה ההופכית.''' | ||
| + | |||
| + | ולא הבנתי בכלל. מה הקשר למטריצות? (אני יודעת מה זו מטריצה מייצגת, קראתי את הקובץ, וגם במחברת, ונראה לי שהבנתי, אבל מה הקשר לתרגיל הזה? בכלל לא הבנתי מה השימוש של המטריצה המייצגת, מלבד לפתרון של תרגילים מסוג "מצא את מטריצה המייצגת"). | ||
| + | |||
| + | ומה זה "בסיס בתמונה", בתרגיל הזה הבסיס הוא <math>\{1,x,x^2\}</math>? את המקור אמצא בעזרת מערכת משוואת כזו: <math>aT(1)+bT(x)+cT(x^2)=1</math> , <math>aT(1)+bT(x)+cT(x^2)=x</math> , <math>aT(1)+bT(x)+cT(x^2)=x^2</math> ? ואז.. מה אני עושה עם המקור הזה? שוב, מה קשורה המטריצה המייצגת? | ||
| + | |||
| + | תודה רבה מראש, מקווה להסבר מפורט. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ניסיתי עכשיו לפתור איך שראיתי לנכון, בלי מטריצות וכל זה... סימנתי <math>T^{-1}(f)=mx^2+nx+d</math>. לאחר מכן אמרתי ש-<math>TT^{-1}(f)=I_{R_2[x]}(f)=f=cx^2+bx+a</math> (ה-<math>f</math> הוא סימון). מצד שני, <math>TT^{-1}(f)=T(T^{-1}(f))=T(mx^2+nx+d)</math> וזה שווה למה שמצאתי קודם, הרי יש לי את <math>T(f)</math>. קיבלתי מערכת של 3 משוואות (לפי המקדמים של <math>x^2</math>, <math>x</math>, <math>1</math>) ואז ביטאתי את <math>m</math>,<math>n</math>,<math>d</math> באמצעות <math>a</math>,<math>b</math>,<math>c</math> וקיבלתי את <math>T^{-1}(f)</math>. | ||
| + | |||
| + | בלי מטריצות, רק אלגברה. הגיוני? או שבכלל לא הבנתי את התרגיל? | ||
| + | |||
| + | |||
| + | ===תשובה=== | ||
| + | *למדנו הרי כיצד למצוא העתקה '''מפורשת''' באמצעות מטריצה מייצגת. | ||
| + | *אנחנו יודעים שהתמונה היא מרחב וקטורי, ולכן יש לה בסיס נסמן אותו <math>u_1,...,u_n</math> | ||
| + | *נמצא w_i כך ש <math>Tw_1=u_1,...,Tw_n=u_n</math> | ||
| + | *לכן <math>T^{-1}u_i=w_i</math> וכך אפשר למצוא את ההעתקה בצורה מפורשת כמו בתרגיל. | ||
| + | |||
| + | דרך שנייה: | ||
| + | *נמצא את המטריצה המייצגת של T | ||
| + | *נהפוך אותה על מנת לקבל מטריצה מייצגת של <math>T^{-1}</math> | ||
| + | *נמצא את ההעתקה במפורש מתוך המטריצה המייצגת, כמו בתרגיל. | ||
====תשובה לתשובה==== | ====תשובה לתשובה==== | ||
| − | תודה, | + | תודה רבה על התשובה! |
| + | |||
| + | לגבי הדרך הראשונה: | ||
| + | *מה זה אומר העתקה '''מפורשת'''? | ||
| + | *האם לכל <math>T(u)=v</math>, מתקיים <math>T^{-1}(v)=u</math>? | ||
| + | *תודה, הצלחתי לפתור את התרגיל בדרך הזו! והתשובה יצאה לי כמו זו שיצאה בדרך שעשיתי קודם (זו שפירטתי למעלה). מעניין איזו קצרה יותר או עדיפה מאיזושהי סיבה. יש העדפה כלשהי באופן כללי, ובמבחן בפרט? | ||
| + | |||
| + | לגבי הדרך השנייה: | ||
| + | *המטריצה המייצגת של <math>T</math> שהיא במקרה הזה פשוט מטריצה <math>[T]_S^S</math> כאשר <math>S</math> הבסיס הסטנדרטי של <math>R_2[x]</math>, בעצם מטריצה שעמודותיה הן (1,0,0), (0,2,3), (0,3,0) - כלומר הצורה הוקטורית של התמונות המתקבלות עבור מקורות מאיברי הבסיס. נכון? | ||
| + | *ישנו משפט שאומר שהמטריצה ההופכית של המטריצה המייצגת של <math>T</math> היא המטריצה המייצגת של <math>T^{-1}</math>? (זה קל להוכחה אבל האם צריך להוכיח בכל פעם?) | ||
| + | *איך מוצאים את ההעתקה במפורש מתוך המטריצה המייצגת? ואיזה תרגיל? | ||
=====תשובה===== | =====תשובה===== | ||
| − | + | *צורה בה אתה יודע לאין איבר כללי הולך. לדוגמא: <math>T(x,y,z)=3x+y+z</math> | |
| + | *כן, זו כמעט ההגדרה של ההעתקה ההופכית. | ||
| + | *יש העדפה לדרכים שאני הצעתי, בניגוד לפתרון הרבה מערכות משוואות. | ||
| − | + | *לא עקבתי ביחס לתרגיל, אבל בגדול מה שאמרת נשמע נכון. | |
| − | + | *צריך לצטט את המשפט בלבד אלא ביקשו מכם להוכיח במפורש | |
| − | + | *עשינו תרגיל כזה בכיתה. אתה מחשב מטריצה מייצגת שמעבירה מהבסיס הסטנדרטי לאנשהו ואז אתה מקבל נוסחא כזו: | |
| + | <math>[T]_B^S[v]_S=[Tv]_B</math>. לכן <math>(x,y,z)</math> הולך לצירוף הלינארי של איברי הבסיס B עם המקדמים מהכפל של המטריצה המייצגת בוקטור <math>(x,y,z)</math> | ||
| − | + | ======השאלות שנשארו====== | |
| + | *בעצם מה שאני צריכה למצוא בתרגיל הזה. אוקיי תודה. | ||
| + | *וניתן להשתמש בזה בלי להוכיח, נכון? | ||
| + | *דרך הפתרון שלי דווקא פשוטה (רק 3 משוואות קלות), אבל באמת כדאי שאבין את עניין השימוש במטריצה המייצגת. | ||
| − | : | + | *טוב. |
| + | *מהו הניסוח המדוייק של המשפט הזה? | ||
| + | *הנוסחה היא ממש משפט, לא? אבל לא הבנתי מה כתבת פה: '''לכן <math>(x,y,z)</math> הולך לצירוף הלינארי של איברי הבסיס B עם המקדמים מהכפל של המטריצה המייצגת בוקטור <math>(x,y,z)</math>.''' בבקשה תסביר ברור יותר, ממש חשוב לי להבין את זה (והתרגיל מהכיתה לא כתוב לי, העדפתי להקשיב). | ||
| − | |||
| − | |||
| − | |||
| + | * | ||
| + | *כן | ||
| + | *חשוב להבין כי יהיו שאלות '''ישירות''' על מטריצה מייצגת שלא תוכלי להתחמק מזה. | ||
| + | |||
| + | * | ||
| + | *תחפשי במחברת הרצאה הכי טוב | ||
| + | *הנוסחא היא משפט כן. את יודעת ש<math>[T]_B^S[v]_S=[Tv]_B</math>. מה המשוואה הזו אומרת? מצד שמאל יש את המכפלה של המטריצה המייצגת בוקטור <math>(x,y,z)</math>. מצד ימין מקבלים את הקואורדינטות של Tv לפי הבסיס B. לכן צירוף לינארי של איברי הבסיס B עם המקדמים שהם המכפלה משמאל שווים בדיוק לTv (הרי זו ההגדרה של קואורדינטות). | ||
| + | |||
| + | מובן? | ||
| + | |||
| + | :אהה.. נראה לי שהבנתי! תודה רבה!! אנסה לפתור את התרגיל בשתי הדרכים. | ||
| + | |||
| + | ==2.15== | ||
| + | מה הכוננה של (v(Ta בסעיף ב'? תודה | ||
| + | |||
| + | :ההגדרה בעמוד 56 | ||
| + | |||
| + | ==מבחן תשסה מועד ב' שאלות אמריקאיות שאלה 10== | ||
| + | למה הטענות הנכונות הן א' וד'? אני חושב ש ב' וג' לא נכונות וגם א' לא נכון. למה א' נכון? א' אומר שכל הפונקציות מR לR הן כל הפונקציות הזוגיות סכום ישר עם כל הפונקציות האיזוגיות. זה לא נכון, כי יש פונקציות שהן לא זוגיות ולא איזוגיות ולא הסכום שלהן, כמו f(x)=x+1 או f(x) =rootX. (שורש של X). ויש גם פונקציות שהן גם זוגיות וגם איזוגיות, כמו f(x)=0 לא? כי אני זוכר מהבגרות שפונקציות זוגיות הן סימטריות ביחס לציר הX (מתקיים) ופונקציות אי זוגיות סימטריות ביחס לציר ה-X "ואז" לY (כלומר לשקף את מה שמימין לציר הX ומשמאל לציר הX ואז זה אמור להיות סימטרי ביחס לציר הY). אני טועה? תודה | ||
===תשובה=== | ===תשובה=== | ||
| − | * | + | * כל פונקציה היא סכום של זוגית ואי זוגית, ספציפית עשינו את זה בתרגיל. <math>f(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}</math> |
| − | * | + | *אתה יודע למה ב' לא נכון? מעל הממשיים הוא כן נכון. הבעייה היא, למשל, מעל <math>\mathbb{Z}_2</math> שם יש את המטריצה <math>\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}</math> שהיא גם סימטרית וגם אנטי סימטרית ושונה מאפס. |
| + | :שתי דברים: דבר ראשון, לא הבנתי מהדוגמה שלך למה כל פונקציה היא סכום של פו' זוגית ואי זוגית (ואני לא זוכר שעשינו את זה בתרגיל). דבר שני, אז מה אם הפונקציה f(x)=0, היא לא גם זוגית וגם אי זוגית? תודה | ||
| − | == | + | ::אתה יכול לוודא בקלות ש<math>\frac{f(x)-f(-x)}{2}</math> אי זוגית ו<math>\frac{f(x)+f(-x)}{2}</math> זוגית. 0 היא בוודאי גם אי זוגית וגם זוגית. לכן החיתוך הוא אפס, בדיוק כמו שאנחנו מצפים מסכום ישר. |
| − | + | ||
| + | ==מבחן תשסה מועד ב' שאלות אמריקאיות שאלה 3== | ||
| + | אוקי, עכשיו אני בטוח שיש פה טעות כלשהי. בתשובות כתוב שאפשרות 3 היא הבחירה הנכונה, כלומר 3 לא נכונה. זה לא הגיוני, כי לפי השאלה, יש לבחור רק תשובה אחת לא נכונה, כלומר אם 3 לא נכונה אז 1 2 ו4 נכונות- אבל תשובה 2 אומרת שאף אחת מהתשובות האחרות היא אינה נכונה, שאת המשפט הזה אפשר להבין ב2 דרכים: | ||
| + | -כל התשובות האחרות לא נכונות, שזה לא יכול להיות כי עם 3 הוא לא נכון זה אומר ש 1 ו4 נכונות בסתירה לכך שכל התשובות האחרות לא נכונות. | ||
| + | -כל התשובות האחרות נכונות, שזה לא הגיוני כי 3 הוא לא נכון. | ||
| + | אז נכון שיש טעות כלשהי? אני חושב שהתשובה ההגיונית היחידה היא 2. תודה | ||
===תשובה=== | ===תשובה=== | ||
| − | + | תשובה 3 היא משפט שקר. | |
| − | + | אתה צודק שגם 2 הוא משפט שקר, זה פשוט בלבול של כותב השאלה. | |
| − | : | + | ==rank== |
| + | הrank של מטריצת האפס הוא אפס, נכון? | ||
| + | :כן | ||
| − | == | + | ==טעות במספר תעודת זהות== |
| − | + | שלום,בציוני הבוחן והתרגילים ישנה אותה טעות במספר תעודת זהות שלי,בשניהם כתוב 205403933 אך המספר הנכון הוא 205413933. | |
| + | אשמח אם תוכלו לתקן זאת | ||
| + | |||
| + | |||
| + | :בסדר, תודה. | ||
| + | |||
| + | ==שאלה על rank== | ||
| + | יהי T:V->V ה"ל וB,C בסיסים בV. מה זה rankT? מה זה rank([T]BC)? (כשBC אומר שיש B קטן בצד למעלה ימין של [T] וC קטן בצד ימין למטה)? תודה | ||
===תשובה=== | ===תשובה=== | ||
| − | + | <math>rank([T]_C^B)</math> זה דרגה של המטריצה המייצגת ואנחנו יודעים את ההגדרה של דרגה של מטריצה. הדרגה של העתקה rankT זה המימד של התמונה (עמוד 56 בחוברת). | |
| − | == | + | ==שאלה ממבחן== |
| − | + | במבחן השני מועד א' שאלה אמריקאית 11, מה זה אומר שT היא מעל השדה Zp? זה אומר שהיא מZp לZp? מה זה אומר? איך זה יכול להיות שT היא מF לF כשF שדה, העתקה לינארית צריכה להיות ממרחב וקטורי למרחב וקטורי, לא? למה התשובה הנכונה היא 3? תודה. | |
| − | + | ===תשובה=== | |
| + | שדה הוא תמיד מ"ו מעל עצמו ממימד 1. לכן זו העתקה ממרחב וקטורי למרחב וקטורי. בשאלה מסתכלים על F כמ"ו מעל Z_p בכלל. | ||
| − | + | בכל אופן לא למדתם מאפיין ולכן השאלה לא ממש רלוונטית. | |
| − | + | ||
| − | + | ==שאלה ממבחן== | |
| + | במבחן השני מועד א' שאלה אמריקאית 10, למה התשובה היא א,ב,ג, ולא כל הטענות נכונות?? הצלחתי למצוא מטריצות כך שכל הטענות יהיו נכונות- | ||
| + | |||
| + | א' וב' שתי מטריצות האפס | ||
| + | |||
| + | ג' A מטריצת האפס וB מטריצה גדולה ללא אפסים | ||
| + | |||
| + | ד' A מטריצה גדולה ללא אפסים וB מטריצת האפס.. | ||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | בד', AB=0 איך הדרגה שלו תהיה שווה לדרגה של A בדיוק? | |
| − | :תודה! | + | ==שאלה ממבחן== |
| + | במבחן השני מועד א' שאלה אמריקאית 9, למה הפתרון הוא 3? שמתי משתנים, דירגתי והגעתי למטריצת הזהות, כלומר כל האיקסים שווים לאפס? זה בטוח לא יכול להיות <math>(0,t,0,0,0)</math>! יש טעות? תודה | ||
| + | |||
| + | ===תשובה=== | ||
| + | למעשה המשתנה השני *חייב* להיות חופשי. בגלל שאם היה לו איבר פותח המטריצה לא הייתה מדורגת כלל. לעומת זאת בעמודות האחרות ניתן להוסיף איבר פותח כך שכל שאר המשתנים יהיו אפס. | ||
| + | כמובן שעוד פתרונות יתכנו, אבל לא פתרונות 1,2,4 בהם המשתנה השני אינו חופשי. | ||
| + | :"בגלל שאם היה לו איבר פותח המטריצה לא הייתה מדורגת כלל. לעומת זאת בעמודות האחרות ניתן להוסיף איבר פותח כך שכל שאר המשתנים יהיו אפס"- סליחה, ממש לא הבנתי למה התכוונת. מה זה איבר פותח, למה המשתנה השני חייב להיות חופשי, מה זה אומר שאם לא היה איבר פותח המטריצה לא הייתה מדורגת? גם אם הייתי יודע מה זה איבר פותח, למה דווקא המשתנה השני חייב להיות חופשי, למה לא השלישי הרביעי החמישי או הראשון? תודה | ||
| + | |||
| + | |||
| + | ::כמו שאמרתי, חלק מהאחרים גם יכולים להיות חופשיים. אבל השני '''חייב''' להיות חופשי. איבר פותח או איבר ציר זה האיבר הראשון בשורה ששונה מאפס. איך יודעים אם משתנה הוא חופשי? אם אין איבר פותח בעמודה שלו. האופציה היחידה לשים איבר שונה מאפס בעמודה של המשתנה השני היא בשורה האחרונה. אבל השורה האחרונה חייבת להיות שורת אפסים על מנת שהמטריצה תהיה אכן מדורגת. | ||
| + | :::מה?? המשתנה השני חייב להיות חופשי כי אין איבר פותח בעמודה שלו? אבל אפשר להחליף בין העמודה השניה לחמישית! והשורה האחרונה לא חייבת להיות שורת אפסים, דירגתי והגעתי לשורה ראשונה עם איבר פותח בעמודה הראשונה, שורה שנייה עם איבר פותח בעמודה השניה וככה לכל השורות! | ||
| + | |||
| + | ::::אי אפשר להחליף עמודות, ממתי מותר? נתונה מטריצה '''בצורה קנונית'''. אתה לא יכול לשים איזה מספרים שאתה רוצה, רק מספרים שישאירו את המטריצה מדורגת קנונית. נובע מכך, '''בהכרח''', שהשורה האחרונה היא שורת אפסים. אחרת יש איבר פותח שאינו נמצא מימין ממש לאיבר הפותח שלפניו (והאיבר הפותח לפניו בעמודה האחרונה). | ||
| + | |||
| + | ==שיעור חזרה ביום ראשון== | ||
| + | שיעור החזרה יהיה במתכונת של שאלות ותשובות, או שהמתרגל יפתור תרגילים? | ||
| − | + | פשוט אני עוברת על כל המחברת ועד עכשיו יש לי בערך 7 שאלות, כדאי לשאול אותן פה, או לחכות לשיעור? (קשה יותר לשאול ולהסביר פה..) | |
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | שיעור החזרה יהיה עם חומר מוכן מראש. | |
| − | + | ||
| − | == | + | פרט לכך, נשאר אתכם כמה שצריך אחרי כן לענות על שאלות (לא כל המתרגלים, אבל לפחות אני). |
| − | + | ||
| − | + | בנוסף, אפשר לרשום פה בוודאי. | |
| − | + | ||
| − | + | :תודה על התשובה המהירה! מי אתה? | |
| + | |||
| + | ::ארז. | ||
| + | :::אה יופי אתה המתרגל שלי. | ||
| + | |||
| + | ==עמוד 49 שאלה 11.8== | ||
| + | עבור מטריצה A=1-0-0,0-1-0 (מסדר 2 על 3), אני טוענת ש-rankA=2. צריך להסביר משהו מעבר ל: "לפי הבסיס הסטנדרטי rankA=2"? | ||
| + | |||
| + | תודה. | ||
===תשובה=== | ===תשובה=== | ||
| − | + | מה הכוונה לפי הבסיס הסטנדרטי? ניתן לומר "זו מטריצה מדורגת. דרגת המטריצה שווה למספר השורות השונות מאפס בצורה המודרגת שלה. יש פה 2 שורות שונות מאפס" | |
| + | :טוב.. פשוט זה נורא ארוך לתרגיל שכולו 2 שורות ><. תודה. | ||
| + | :יש לי רעיון, אכתוב "דרגת מטריצה מדורגת שווה למספר השורות השונות מ-0 בצורתה המדורגת" ואסמן בכוכבית, ואז בכל פעם אכתוב "לפי * rankA=2". אחרת, זה נורא ארוך וסתמי, לחזור על אותו המשפט 9 פעמים! | ||
| − | + | ==שאלה ממבחן 2005 מועד א== | |
| − | + | במבחן השני מועד א' שאלה אמריקאית 2, z^3=x3 כשx שווה לצמוד של z. למה אף אחת מהתשובות לא נכונה? יצא לי שim(z)=0 גם כשהתעסקתי בZ כa+bi וגם כrcisO. זו טעות או שאני טועה? תודה | |
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===תשובה=== | |
| − | : | + | מה לגבי <math>cis(\frac{\pi}{3})</math>? |
| + | |||
| + | ==2.11== | ||
| + | בשאלה 2.11 בב' כתוב שיש העתקהה s:v -> v וs לא שווה לאפס. לא נאמר ש S העתקה לינארית, האם כשאני מוכיל שב' שקול לא' אני צריך להוכיח שS לינארית, או שהיא סתם העתקה? | ||
| + | תודה | ||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | הכוונה לS העתקה לינארית, אחרת מה קשור משפט ההגדרה? | |
| − | + | ==שאלה ממבחן== | |
| − | ::תודה! | + | אם נתון לי ש |
| + | :T(1+2x+xx)= (1,1,2) | ||
| + | :T(1+x+2xx)=(2,1,1) | ||
| + | :T(2+x+xx)=(1,2,1) | ||
| + | אז אני יכול להגיד שפשוט T(axx+bx+c)= (c,b,a) ואז זה ממש ממש פשוט להוכיח שT חח"ע ועל? | ||
| + | ועוד שאלה קטנה, כתוב בתחילת השאלה שT העתקה לינארית, אז זה אומר שכדי להוכיח שT איזומורפיזם אני לא צריך להוכיח שהיא העתקה לינארית נכון? תודה. | ||
| + | |||
| + | ===תשובה=== | ||
| + | אי אפשר פשוט להגיד את זה, צריך להוכיח את זה. | ||
| + | |||
| + | אף פעם לא צריך להוכיח את הנתון. אם רשום "נתונה העתקה לינארית" אין צורך להוכיח את זה. | ||
| + | |||
| + | ==2.8== | ||
| + | סלחו לי אם אני כותב את התשובה, אבל לא קיבלתי מענה האם ההוכחה שלי נכונה או לא- האם אני יכול להוכיח שv=imT1=imT2 כך? | ||
| + | x שייך לimT1 וy שייך לimT2 וv שייך לV. | ||
| + | :x+y /T1() -> =T1(x)+ T1(y) /+T2(v) -> =T1x+T1y+T2v ->T2() -> =T1T2x+T1T2y+T2T2v =0+T2T2v =T2v | ||
| + | :v /T1() -> =T1v /+T2v -> = T1v+T2v =Iv=v /T2() -> =T2v | ||
| + | (עשיתי אותן פעולות והגעתי לכך ששני האגפים שווים). ואז רק להוכיח שחיתוך הimים זר, וזה בסדר? או שזה לא נכון? תודה! | ||
| + | |||
| + | :לא קיבלת מענה, כי בשביל זה יש בדיקת תרגילים. ביום ראשון יפורסמו פתרונות לתרגילים בכל מקרה. | ||
| + | ::אני לא יקבל את התרגיל עד המבחן ואני רוצה לדעת אם הפתרון שלי גם בסדר... | ||
| + | |||
| + | :::אז תשאל שוב יום ראשון. | ||
| + | ::::למחוק את השאלה? | ||
| + | |||
| + | :::::זה בסדר, תודה :) | ||
| + | |||
| + | ==6.14== | ||
| + | סעיף א: האם צריך להשלים את הה"ל לפי הבסיס הסטנדרטי , ואז למצוא את T בצורה מפורשת? וכן בסע' ב' האם לשלוח את הוקטורים הנתונים ל-0, ולהמציא וקטור שלישי (בת"ל בשניים הנתונים) ו"לשלוח אותו" לסתם וקטור כלשהו, ואז למצוא את T... אבל אז סע' ב' וג' יכלים להיות זהים? נכון? | ||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | בסעיף א' צריך למצוא את ההעתקה בצורה מפורשת. מה להשלים למה זה בחירה שלך, העיקר שיקיים את תנאיי הסעיף. | |
| + | |||
| + | כנ"ל לגבי הסעיפים האחרים. | ||
| + | |||
| + | בוודאי שכל העתקה לינארית מסעיף ג' עונה על התנאים של סעיף ב'. | ||
| + | ====שאלה בקשר לתשובה==== | ||
| + | האם צריך להראות איך הגענו לההעתקה המסויימת או שפשוט להראות שהיא מקיימת את התנאים? | ||
| + | |||
| + | =====תשובה===== | ||
| + | צריך לפרט בתרגיל הזה, שכן הוא בוחן את ההבנה של משפט ההגדרה, ומציאת העתקה המפורשת מתוך ההגדרה | ||
| + | :התכוונתי האם צריך להסביר איך הגעתי להעתקה עצמה או להראות שזה מתקיים עבור בסיס כלשהו ואז להשתמש במשפט ההגדרה ולהגיע לכללית? (האם צריך להסביר למה בחרתי ככה את ההעתקה עבור האיברים של הבסיס ואיך הגעתי אליה??) ודבר נוסף האם מותר לי להגדיר את ההעתקה שלי כלינארית ואז להשתמש במשפט ההגדרה (כי אני נותן את הערכים שאליהם נשלח הבסיס) ולהגיע להעתקה הכללית? (מותר לי להגדיר אותה כלינארית בכלל בתרגיל הזה? לא שאני רואה דרך אחרת..) | ||
| + | |||
| + | ==1.28== | ||
| + | האם זה נכון להוכיח ש imT1=kerT2, ומכאן נובע שהסכום ישר לפי 2.7 ב. כי T2 אידמפוטנטית? | ||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | אם זה נכון זה בסדר, ואם זה לא נכון אז לא :) | |
| − | + | ==כמה שאלות== | |
| + | *'''דורש הוכחה או טריוויאלי?''' קבוצה D פורשת מ"ו V. ב-D יש n איברים. האם צריך להסביר למה מכך נובע ש- dimV<=n? (אפשר להניח בשלילה ש-k=dimV>n ואז אם d שייך ל-D, נוסיף ל-D עוד k-n איברים מהצורה ad כאשר a בשדה. נקבל קבוצה חדשה E שפורשת את V וגם dimE=k לכן E בסיס ל-V, אבל E ת"ל כי <math>d+a_1ad=0</math> כאשר <math>a_1</math> בשדה אבל <math>a_1=-a^{-1}</math> שונה מ-0. קיבלנו סתירה לכך שבסיס הוא בת"ל, מ.ש.ל) ההוכחה די ארוכה והיא לא מטרת התרגיל (11.2), אבל מצד שני, האורך שלה מראה על כך שהיא לא ממש טריוויאלית.. בקיצור - צריך או לא צריך? | ||
| + | *מה זה cspan? אם יש כזה דבר בכלל..? | ||
| + | *הציון שלי של תרגיל 3 לא מופיע, למה ומה לעשות בנושא? (הגשתי אותו!) | ||
| − | + | תודה מראש!! | |
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | *לא צריך להוכיח את זה אלא מבקשים במפורש. מספיק לצטט את המשפט מההרצאה. | |
| − | אני | + | *אני מנחש שזה קיצור של Columne Spane כלומר מרחב העמודות. אני לא נתקלתי בזה, אני לא יודע אם ראיתם את זה בהרצאה או לא. |
| − | + | *לשלוח למתרגל שלך מייל בנושא. | |
| + | ====תשובה לתשובה==== | ||
| + | תודה! | ||
| + | *איזה משפט בדיוק? | ||
| + | *אני ראיתי את זה בשאלה שמתחת לזו... | ||
| + | *אוקיי תודה. | ||
| − | |||
| − | + | :לא יודע, תפתח מחברת ותחפש. כנראה שיהיה מספיק לכתוב "לפי משפט, מספר האיברים בקבוצה פורשת גדול או שווה למימד" | |
| − | + | ||
| − | + | ::נראה לי שהמשפט שאומר שאם יש קבוצה שפורשת את V, וקבוצה בת"ל מוכלת ב-V אז מספר האיברים בפורשת גדול שווה ממספר האיברים בבת"ל. | |
| − | + | ||
| − | + | ==המבחן== | |
| − | + | ביום שלישי יש מבחן בלינארית. כמה זמן המבחן? מתי הוא מתחיל? כמה שאלות? מה המבנה? | |
| + | |||
===תשובה=== | ===תשובה=== | ||
| − | + | מה שאמרו בהרצאה. אם לא אמרו, אפשר לשאול ביום ראשון בחזרה | |
| − | + | מה אמרו בהרצאה? אני לא יכול להגיע ביום ראשון לחזרה, אתם משאירים אותי פה במתח. | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | == 11.10 == | ||
| + | האם אני יכול להגיד ש- dim(cspan(A)+cspan(B))=rank(A+B)? | ||
===תשובה=== | ===תשובה=== | ||
| − | + | לא, זה לא נכון. קח (A=(-B | |
| − | == שאלה == | + | ==שאלה 6.14== |
| − | + | אפשר הכוונה לגבי 6.14? תודה רבה! | |
| + | |||
| + | :הרמז שרשום שם מכוון מצויין.. משפט ההגדרה, השלמה לבסיס. אם תוכל לכוון אותי לבעייה, אני אוכל לכוון אותך לפתרון. | ||
| + | ::התכוונתי לגבי א'. תודה | ||
| + | :::כן, לגבי א'. משפט ההגדרה במפורש. הרי התמונה של ההעתקה היא המרחב הנפרש על ידי ה-w_i מהמשפט. | ||
| + | |||
| + | ==2.8== | ||
| + | מה זה אומר ש T1+T2 = Iv? אני יודע מה זה Iv, אני מתכוון ל-מה זה אומר הסכום שלהם? כאילו ש T1v1+T2v2=v1+v2 או ש T1v+T2v=v? או מה? זה ממש לא מובן. תודה | ||
===תשובה=== | ===תשובה=== | ||
| − | למדנו | + | תקרא את אותה שאלה עם התשובה למטה. |
| + | :סליחה לא שמתי לב! אני די בטוח שלא למדנו את זה אבל לא נורא. תודה | ||
| + | |||
| + | ::אני בטוח לחלוטין (כמעט) שכן למדתם את זה ולכן זה דיי נורא כי זה חומר חשוב למבחן. | ||
| + | ===שאלה נוספת=== | ||
| + | וכשכתוב בב' T1T2, הכוונה היא הפעם לכפל של העתקות, כמו סכום? כי בדרך כלל זה הרכבה, אבל עכשיו נראה יותר מתאים שזה יהיה כפל. נכון? תודה | ||
| + | |||
| + | :ואז איך תגדיר? כפל של שני וקטורים? אין כזה דבר כפל של שני וקטורים. כפל בין העתקות לינארית הוא בלבד הרכבה. כפי שלמדנו <math>T^2=TT=T\circ T</math> | ||
| + | ::אה, חשבתי שאם א. זה חיבור אז ב. זה יהיה כפל כזה D=TS -> D(v) = T(v)*S(v) אבל לא משנה. | ||
| + | ===עוד שאלה, לגבי דרך הפתרון=== | ||
| + | האם אני יכול להניח שקיימים x ששייך לimT1 וy ששייך לimT2 ואז להראות שאחרי כמה פעולות imT1+imT2 שווה לv ששייך לV אחרי אותן פעולות? אני ממש לא בטוח אם זה נכון, יש משהו לא נכון בהוכחה שלי? בנוסף, אני חושב שלא השתמשתי בעובדה שזה סכום ישר. זה בסדר? תודה! | ||
| + | |||
| + | :אין עובדה שזה סכום ישר, זה מה שצריך להוכיח. אם לא הוכחת את זה אז זה לא בסדר. | ||
| − | + | :ואתה לא צריך להראות שסכום של x וy הוא איבר בV זה טריוויאלי מסגירות. אתה צריך להוכיח ש'''כל''' v בV הוא מהצורה v=x+y עבור x,y כלשהם בIm-ים המתאימים. | |
| + | ::אוקיי, אז אם אני לוקח v ששייך לV, ואחרי כמה פעולות מגיע ממנו לX+Y, זה בסדר? | ||
| + | ::האם מותר לי גם (יהיה לי הרבה יותר קל אם כן) להניח שקיימים v,x,y כמו מקודם, ואז להראות אחרי כמה פעולות ש v=a וגם x+y=a | ||
| + | ::(a ביטוי מסוים שלא אכתוב כדי לא לגלות את התשובה). זה בסדר? אפשר להגיד שאם זה ואם אין חיתוך בין הim-ים, אז ה-דרוש מתקיים? | ||
| + | ::ועוד דבר, אני יכול להניח שT1 וT2 הפיכות? תודה! | ||
| − | + | ::: אי אפשר להניח דברים שלא בנתון. ושוב, אתה חייב להראות ש'''כל''' v הוא מהצורה הנ"ל. איך תעשה את זה? זו החלטה שלך. הניסוח שלך קצת מצחיק- תקח x,y,v כללים ותוכיח שתמיד x+y=v? הרי וודאי לא יכול להיות שתצליח בזה. | |
| − | == | + | ==2.7== |
| − | מה | + | אם אני מוכיח ב א' T היא העתקה הזהות זה בעצם מקיים את מה שהם מבקשים? או שצריך להראות שייש מקרים עבורם T שווה למינוס העתקת הזהות?(לפי מה שניסיתי לראות המקרה השני בכלל לא הגיוני וניתן לסתור אותו,אז אם צריך להראות שניתן שיתקיים שT שווה למינוס אז זו בעצם הפרחה, לא?) |
===תשובה=== | ===תשובה=== | ||
| − | + | הלוגיקה חשובה במתמטיקה. אני אענה לשאלה, אבל חשוב לי להבהיר שאתם צריכים להיות מסוגלים להבין שאלה כזו לבד. | |
| − | ==שאלה | + | כאשר אומרים הוכח/הפרך, יש לומר אם המשפט הוא משפט שקר או משפט אמת. |
| − | + | ||
| + | במקרה הזה המשפט הוא: | ||
| + | '''T המקיימת את תנאי השאלה היא בהכרח העתקת הזהות או מינוס העתקת הזהות.''' | ||
| + | |||
| + | אם כל T שמקיימת את תנאי השאלה היא העתקת הזהות או מינוס העתקת הזהות אזי המשפט נכון (מהגדרה). | ||
| + | |||
| + | לעומת זאת, אם קיימת T שמקיימת את תנאי השאלה ושונה מהעתקת הזהות '''וגם''' שונה ממינוס העתקת הזהות אזי המשפט הוא משפט שקר והפרכנו אותו. | ||
| + | :ככה חשבתי, פשוט זה נראה לי מוזר שבכלל הוסיפו את העניין עם המינוס אם הוא לא משנה בכלל, אז העדפתי לשאול. תודה | ||
| + | ::יופי. תמיד טוב לשאול. | ||
| + | ===שאלה בקשר לשאלה והתשובה שנשאלו פה=== | ||
| + | רגע, אבל מה עם העתקת האפס, זה לא סותר את מה שאמרתם, העתקת האפס לא שווה להעתקת היחידה? לא? | ||
| + | |||
| + | |||
| + | יש לשים לב כי העתקה אידמפוטנטית מוגדרת <math>T^2 = T</math> פרט ל-0 (בדר"כ) - בהסתמך על הערך "אידמפוטנט" [http://he.wikipedia.org/wiki/%D7%90%D7%99%D7%93%D7%9E%D7%A4%D7%95%D7%98%D7%A0%D7%98%D7%99%D7%95%D7%AA] | ||
| + | |||
| + | == 1.28 == | ||
| + | המטריצה המייצגת יצאה לי (x^2 2*x+3 3*x) זה הגיוני?ואז אני מדרג?הרי זה כמו וקטור שורה איך אני יכול לדרג? | ||
| + | (לא ענית לי למטה..)תודה! | ||
===תשובה=== | ===תשובה=== | ||
| − | + | כי מה שרשמת זה לא מטריצה. העמודות של המטריצה צריכות להיות וקטורי הקואורדינטות, בוודאי פולינום אינו יכול להיות עמודה של מטריצה. | |
| + | |||
| + | ממליץ בחום רב לקרוא את המסמך על קואורדינטות ומטריצות מייצגות, יש שם דוגמאות והסברים לכל התהליך. | ||
| + | |||
| + | ==שאלה (שקשורה ל6.14)== | ||
| + | האם העתקה T:V->W חייבת להיות מוגדרת לכל v בV? אני יודע שבהעתקות, לא חייב להיות לכל וקטור בW מקור, כי אני זוכר שהעתקה יכולה להיות על ולא על, אבל האם היא חייבת "לקחת" את כל הקטורים מV אל איברים בW אל לא? | ||
| + | למשל, אם אני מגדיר העתקה מR4 לR4, האם אני יכול להגיד אותה כך? T(a,b,00) = T(0,0,a,b) אפילו שהוא לא מוגדר לכל V, או לא? תודה | ||
| + | |||
| + | ===תשובה=== | ||
| + | חייב להיות מוגדר לכל v, באופן כללי פונקציה צריכה להיות ח"ע ושלימה (כמו בבדידה) | ||
| + | |||
| + | == 1.14 == | ||
| + | אפשר בבקשה הכוונה איך אני מוכיח את א'? עם ב' הסתדרתי.. | ||
| + | |||
| + | :אין סעיפים בשאלה 1.14 | ||
| + | |||
| + | ::התכוונתי להעתקת האפס!! | ||
| + | |||
| + | :::מוכיחים את זה באמצעות הקריטריון המקוצר לבדיקת העתקה לינארית. | ||
| + | |||
| + | ::::אני יכול לעשות מעבר כזה: T(v+u) =0 כיוון ש לכל v ששיך לV מתקיים T(v)=0? | ||
| + | |||
| + | :::::מן הסתם... זו ההגדרה של העתקת האפס. | ||
| + | |||
| + | :::::תודה:) | ||
==שאלה== | ==שאלה== | ||
| − | + | הדרגה של מטריצה עם 2 שורות ו2 עמודות שונות משורות אפסים, היא 2 או 4? לפי תשובה קודמת, נראה שכתבתם שהדרגה היא 2, | |
| − | + | אבל זה מביא לסתירה מסוימת, כי אם rank(A) =2 אם A מטריצה מגודל 2 על 2, אז זה אומר גם שהמימד של המרחב R2x2 הוא 2, לא? אבל חשבתי שהמימד של המרחב R2x2 הוא 4, כי בבסיס שלו 4 איברים {(0,0,0,1)(0010)(0100)(1000)} ? איפה אני טועה? תודה | |
| − | תודה | + | |
| + | ===תשובה=== | ||
| + | לפי תשובה קודמת, ראינו מטריצה כזו עם דרגה 1. אין קשר בין המימד של מרחב המטריצות, לפי המימד של מרחב השורות של המטריצה. הדרגה של מטריצה בגודל nxm היא קטנה שווה למינימום בין n,m. לעומת זאת מימד כל המטריצות הוא nm. | ||
| + | |||
| + | אם המטריצה בצורה מדורגת, הדרגה שלה היא '''מספר השורות השונה מאפס'''. בפרט, הדרגה לא יכולה להיות גדולה ממספר השורות. | ||
| + | :כמה שאלות: -מהי הגדרה של הדרגה של מטריצה? אם היא קטנה או שווה למינימום בין M,N, זה אומר שאי אפשר לחשב אותה במדויק? | ||
| + | :-אם יש מטריצה (מטריצות) שנראית כך: a, b, c, a+b+c | ||
| + | :(a וb בשורה הראשונה וה2 האחרים בשורה השניה), אז מימד המטריצות האלה הוא עדיין MN? אפילו שאחד האיברים במטריצה תלוי באחרים? | ||
| + | :-rankT כך שT הוא ממטריצות MxN למטריצות מאותו הגודל, הוא MN או המינימום? יש דבר כזה rankA וגם rankT כשA מטריצה וT העתקה? הם 2 סימונים ל2 דברים שונים? תודה רבה | ||
===תשובה=== | ===תשובה=== | ||
| − | + | ההגדרה רשומה בעמוד זה, מספר פעמים. למשל [[#שאלה לתשובה]] ושתי שאלות מתחתיה. | |
| − | + | אם תיקח תת מרחב של מרחב כל המטריצות שלא מכיל את כל המטריצות האפשריות, המימד שלו בהכרח יהיה קטן יותר. לגבי הדוגמא הספציפית צריך לוודא שזה אכן תת מרחב אחרת אין הגדרה למימד שלו. | |
| + | |||
| + | rankT היא הדרגה של העתקה, אני לא יודע אם למדתם את זה או לא. אם כן, יש הגדרה במחברת שלכם. אם T העתקה לינארית ממרחב המטריצות למרחב המטריצות, היא העתקה בין מרחבים וקטוריים ממימד NM ולכן המטריצה שמייצגת אותה היא מגודל NMxNM, ולכן יכול להיות שהדרגה של המטריצה המייצגת הינה NM. | ||
| + | ::::תודה לגבי כל השאר, יש לי רק עוד דבר לא פתור: נניח שיש מטריצה (בוא נגיד, מסדר 2 על 2) כאשר אחד או יותר מהמקומות במטריצה הוא תלוי\ים במקומות האחרים (כמו בדוגמה שנתתי קודם, רק אם הדוגמה שנתתי לא טובה (כי היא לא תת מרחב וכדומה) אז דוגמה אחרת דומה -- המימד של המטריצות מהסוג הזה הוא עדיין MxN או לא? תודה. | ||
| + | |||
| + | |||
| + | דוגמא: | ||
| + | |||
| + | יהי מרחב המטריצות <math>V=F^{2\times 2}</math> ויהי <math>W=\{A\in V : a_{11}+a_{12}+a_{21}=a_{22}\}</math>. | ||
| + | |||
| + | אזי קל לוודא שW תת מרחב של V ושהבסיס שלו הינו | ||
| + | <math>B=\{ | ||
| + | \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}, | ||
| + | \begin{bmatrix} 0 & 1 \\ 0 & 1\end{bmatrix}, | ||
| + | \begin{bmatrix} 0 & 0 \\ 1 & 1\end{bmatrix} | ||
| + | \}</math> | ||
| + | |||
| + | לכן המימד של W הינו 3. | ||
| + | |||
| + | המימד של V לעומת זאת הוא 4. | ||
| + | |||
| + | :איך מצאת את הבסיס של W? | ||
| + | |||
| + | == 1.28 == | ||
| + | מה הכוונה וקטור כללי מ R2[X ? נניח (1,1,1) הוא טוב? | ||
| + | |||
| + | ===תשובה=== | ||
| + | |||
| + | 1. (1,1,1) הוא וקטור '''ספציפי''' - ההפך מ'''כללי''' | ||
| + | |||
| + | 2. במרחב הפולינומים <math>\mathbb{R}_2[x]</math> הוקטורים הם '''פולינומים''' מדרגה קטנה שווה 2. לכן וקטור כללי במרחב זה הוא <math>a+bx+cx^2</math> | ||
| + | |||
| + | :את האמת שזה מה שחשבתי רק שלא הייתי בטוח.. | ||
| + | :בכל מקרה, איך אני מחשב את ההעתקה ההפיכה? | ||
| + | |||
| + | ::יש כמה דרכים. אחת מהן למדתם בהרצאה- בעזרת ההופכית של המטריצה המייצגת. הדרך השנייה היא לפי משפט ההגדרה - מספיק לבחור בסיס בתמונה ולראות מה המקור שלו וכך אפשר לחשב את המטריצה המייצגת של ההעתקה ההופכית. | ||
| + | |||
| + | :::ראיתי הגדרה שאומרת: תהי f:A->B פונקציה. אם קיימת g:B->A כך ש f הרכבה g =למטריצה היחידה של A ו g הרכבה f= למטריצת היחידה של B נאמר | ||
| + | :::שf הפיכה וg נקראת הפונקציה ההופכית של f. | ||
| + | :::אי אפשר להשתמש בזה עבור הרכבה של העתקות לינאריות? | ||
| + | |||
| + | :::: אפשר לומר את זה על העתקות לינאריות, עם הסייג הבא: הרכבה של העתקות לינאריות אינה מטריצה אלא העתקה. כלומר ההרכבה של ההעתקות היא ההעתקת הזהות והמכפלה של המטריצות המייצגות היא מטריצת היחידה (שכן המטריצה המייצגת של העתקת הזהות מבסיס לעצמו היא תמיד מטריצת היחידה). | ||
| + | |||
| + | ::::המטריצה המייצגת יצאה לי (x^2 2*x+3 3*x) זה הגיוני?ואז אני מדרג?הרי זה כמו וקטור שורה איך אני יכול לדרג? | ||
== שאלה == | == שאלה == | ||
| − | |||
| − | |||
| − | + | צריך למבחן לדעת את העתקת האינטגרל, הנגזרת ועוד נושאים המוזכרים בחוברת של בועז צבאן ולא למדנו אותם?? | |
| + | |||
| + | === תשובה=== | ||
| + | אין צורך לדעת דברים שלא נלמדו בהרצאה, בתרגיל או נתנו בשיעורי הבית. | ||
| + | |||
| + | כמובן שלא מזיק לפתור תרגילים נוספים, אבל אין צורך לזכור הגדרות אחרות. | ||
| + | |||
| + | ==שאלה למתרגלים (או למתרגל הספציפי שלי, אדם צ'פמן== | ||
| + | למדנו נושא שלם (דטרמיננטות) שלא הזכרנו אותו אפילו בתרגול עם אדם צ'פמן. למה? המרצה אמר שהוא יכול להיות במבחן! | ||
| + | תודה. | ||
| + | |||
| + | :מוזר, אנחנו מהקבוצה השנייה(עם אלי בגנו) לא למדנו דטרמיננטות בכלל גם לא בתרגול. | ||
===תשובה=== | ===תשובה=== | ||
| − | + | אם הנושא יהיה במבחן, הוא יהיה בהתחשב בכך שלא היה תרגול. בהסמך על מה שלמדתם בהרצאה בלבד. | |
| − | + | כמובן שלמי שלא למד את זה בהרצאה, זה לא יהיה במבחן. | |
| − | + | ==תרגיל 11.8== | |
| + | מבקשים ממני בתרגיל לתת דוגמות למטריצות אשר מקיימות את התנאי המתבקש. | ||
| + | האם אני צריך להסביר כיצד הגעתי לדרגה של המטריצות A ו-B שבחרתי או שפשוט לכתוב: "דרגתה של המטריצה A שנבחרה היא ... " | ||
| + | ואותו כנ"ל עבור AB. | ||
| − | + | תודה מראש, גל. | |
| − | : | + | :צריך רק להראות שהדרגה שלהן היא אכן כפי שאתה טוען. |
| − | + | ||
| − | + | ==תרגיל 11.2== | |
| + | האם x הוא בהכרח וקטור מסדר n*1 או שהוא יכול להיות מטריצה? | ||
| + | ===תשובה=== | ||
| + | הכוונה היא שb וx שניהם וקטורי עמודה (כלומר מגודל nx1 כפי שציינת) | ||
| + | :תודה! | ||
| + | :ועוד שאלה: כאשר נתון ש-<math>V</math> הוא מרחב העמודות של <math>A</math>, האם אני יכולה פשוט בלי להסביר כלום לכתוב ש: <math>V=span\{v_1,v_2,...,v_n\}</math> כאשר <math>v_1,v_2,...v_n</math> הם וקטורי העמודות של <math>A</math>? | ||
| − | + | ::כן, זו ההגדרה. | |
| − | + | ==בסיס== | |
| − | + | הוצאתי חוברת לינארית מהספרייה, ובספר כתוב שכדי לוודא שוקטורים מסויימים a1,a2,...ak בת"ל, צריך לשים את הוקטורים כעמודות של מטריצה הומוגנית, ואז לצטט את שני המשפטים הבאים: במטריצה המורכבת מהעמודות a1,a2,...,ak,b (כך שכל עמודה היא וקטור), הוקטור b הוא צירוף לינארי של a1,...,ak כך שהמקדם של ai לכל i הוא xi אם"ם (x1,...xk) הוא פתרון של המערכת שלמעלה. בנוסף ידוע כי מטריצת מקדמים מצומצמת (כלומר מקדמים של מערכת משוואות לינאריות הומוגניות) היא שקולה למטריצת היחידה אם"ם אין למערכת פתרון לא טריוויאלי. כלומר נוכיח שהמטריצה שהרכבנו מהעמודות a1,...,ak,b שקולה למטריצת היחידה עפ"י פעולות שורה אלמנטריות, ולפי זה פתרון המערכת x1,...,xk הוא טריוויאלי כלומר 0=(x1,...,xk) ולכן ל- 0=x1a1+x2a2+...+xkak יש רק פתרון טריוויאלי לכן לפי הגדרה הווקטורים a1,...,ak בת"ל. | |
| + | |||
| + | השאלה שלי היא האם מספיק לנמק: ידוע שאם מטריצה שקולה למטריצת היחידה אז כל עמודותיה בת"ל? | ||
| + | נימוק כזה קצר יכול לחסוך המון זמן וכאב ראש... | ||
| − | |||
| − | |||
===תשובה=== | ===תשובה=== | ||
| − | + | למדנו את התיאור הראשון בתרגיל - וגם השתמשנו בזה בפתרון תרגיל 3 (בקובץ המצורף). כמו כן למדנו שניתן לדרג את המטריצה ולראות האם שורות התאפסו לנו. אלה שתי שיטות שונות ושתיהן נכונות. | |
| − | + | חשוב לשים לב ששקילות למטריצה היחידה היא רלוונטית רק כאשר מדובר על מטריצה ריבועית. וקטורים יכולים להיות בת"ל גם אם תשים אותם בעמודות מטריצה והיא תהיה לא ריבועית. | |
| − | + | ||
| − | + | חשוב לזכור שכאשר אנו שמים וקטורים בעמודות ומדרגים - אנו מסתכלים על מרחב הפתרונות. כאשר אנו שמים את הוקטורים בעמודות ומדרגים - אנו מסתכלים על מרחב השורות. | |
| − | == | + | == 11.10 == |
| − | + | המטריצות A B הן שתיהן מגודל MXN?ובהוכחה אני אמורה להניח שהשורות הן בת"ל ושהדרגה שווה למס' השורות? | |
| + | אם שתי המטריצות הן מגודל MXN אז מה הדרגה? | ||
===תשובה=== | ===תשובה=== | ||
| − | + | לעולם לא מניחים דברים שלא כתובים בנתון. הגדלים של המטריצות נתונים - וזה נכון. | |
| − | + | השורות לא חייבות להיות בת"ל בכלל. | |
| − | + | ||
| + | == שאלה לתשובה == | ||
| − | + | תודה על התשובה אבל לא כ"כ עזרת לי, ברור לי שאי אפשר להניח משהו שהוא לא נתון, השאלה שלי היתה האם | |
| − | + | כדי להוכיח את מה שרצו אני מניחה שהם בת"ל,הרי במקרה כללי אני חייבת להניח את זה..לא?ובנוסף לא ענית לי מהי הדרגה | |
| + | של מטריצה(כללית, כלומר שלא יודעם את אבריה) MXN?מימד מרחב השורות/העמודות? | ||
| − | + | ===תשובה=== | |
| + | זה כמו לשאול: האם x זוגי? התשובה המתבקשת כמובן היא תלוי מהו x. | ||
| + | אי אפשר להניח ששורות המטריצה בת"ל, הרי בוודאי יש מטריצות ששורותיהן תלויות לינארית. למה שתניחי דבר שהוא לא בהכרח נכון? | ||
| − | + | אין כזה דבר דרגה של מטריצת כללית. שוב, הדבר דומה לשאלה מהם הגורמים הראשוניים של מספר כללי x. | |
| − | == | + | |
| − | + | כאשר מנסים לפתור תרגיל כזה צריך לגשת אליו בצורה טכנית. לתת שמות לשורות המטריצות A,B ואז לראות מהן שורות המטריצה A+B, ואז לראות איך אפשר לחשב את הדרגה כפונקציה של השורות האלה וככה לנסות לפתור את התרגיל. | |
| + | |||
| + | |||
| + | באופן כללי יש משפט לפיו דרגת המטריצה = מימד מרחב העמודות = מימד מרחב השורות = מספר המשתנים התלויים במערכת ההומוגנית = מספר השורות השונות מאפס בצורה המדורגת של המטריצה | ||
| + | |||
| + | ==תרגיל 2.8== | ||
| + | מה הכוונה ב(א) שכתוב <math> T1 + T2 = Iv </math> ? כלומר מה הכוונה בחיבור העתקות ליניאריות? תודה רבה... XD | ||
===תשובה=== | ===תשובה=== | ||
| − | + | כמו שלמדנו בהרצאה ובתרגיל על המרחב הוקטורי של העתקות לינאריות - <math>Hom(V,W)</math>: | |
| − | == | + | יהיו 2 העתקות לינאריות T,S. נגדיר את ההעתקה הלינארית שהיא החיבור שלהן D=T+S, על ידי <math>\forall v\in V :D(v)=S(v)+T(v)</math> |
| − | + | ||
| − | + | ===תשובה לתשובה=== | |
| − | + | ||
| − | + | תודה רבה XD :P :) :D | |
| + | |||
| + | ==מרחב עמודות ***עוד שאלה***== | ||
| + | איך מחשבים את הדרגה של A, כלומר את מספר האיברים בבסיס של מרחב העמודות של A? איך מוצאים את הבסיס? | ||
| + | מהי הדרגה של מטריצת האפס? למה? תודה. | ||
===תשובה=== | ===תשובה=== | ||
| − | + | *הדרגה של המטריצה היא מספר השורות השונות מאפס בצורה המדורגת שלה. | |
| + | |||
| + | *אפשר למצוא בסיס למרחב העמודות על ידי: | ||
| + | **שחלוף המטריצה A | ||
| + | **דירוג המטריצה המשוחלפת | ||
| + | **שורות הצורה המדורגת של המטריצה המשוחלפת השונות מאפס, מהוות בסיס למרחב העמודות (כאשר מסתכלים עליהן כעמודות כמובן) | ||
| + | *מטריצה האפס היא בצורה מדורגת, אין שורות שונות מאפס ולכן הדרגה היא אפס. | ||
| + | :תודה, אבל נראה לי (לפי הגיון) שהדרגה של מטריצה היא מספר השורות שגם לא תלויות אחת בשניה (בת"ל), לא? נגיד המטריצה | ||
| + | |||
| + | 1 2 | ||
| + | |||
| + | 2 4 | ||
| + | |||
| + | הדרגה שלה היא 1 או 2? תודה. | ||
| + | |||
| + | :הדרגה היא אחד. המושג הכללי שאתה מתאר (מספר השורות שלא תלויות אחת בשנייה) מוגדר במדויק - הוא נקרא מימד. מימד הוא מספר האיברים בבסיס. ואם תביא את המטריצה הזו לצורה מדורגת תראה בקלות שיש רק שורה אחת שונה מאפס בצורה המדורגת, והיא מהווה בסיס למרחב השורות. | ||
| + | |||
| + | ==תרגיל 11.2ב== | ||
| + | מהי המטריצה A|b? | ||
| + | |||
| + | :המטריצה A שהוסיפו לה מימין את העמודה b. | ||
| + | |||
| + | == סכום ישר == | ||
| + | |||
| + | לא הבנתי עד הסוף את הנושא של הסכום הישר! אתה יכול לתת דוגמא? | ||
| + | |||
| + | גם היתה דוג' בהרצאה שלא ממש הבנתי, | ||
| + | |||
| + | V=R^3 u=sp{(1,1,1)}, w={(x1,x2,x3)|x1+x2+x3=0, x1,x2,x3 in R טענה- v=u+w | ||
| + | |||
| + | צ"ל : | ||
| + | |||
| + | 1. U+W מוכל בV. | ||
| + | |||
| + | 2.V תת מרחב של U+W | ||
| + | |||
| + | 3.U חיתוך W שווה 0. | ||
| + | |||
| + | למה צריך להוכיח את 2?? | ||
| + | |||
| + | ===תשובה=== | ||
| + | הביטוי <math>V=U\oplus W</math> אומר את שני הדברים הבאים לפי הגדרה: | ||
| + | |||
| + | א. V=U+W | ||
| + | |||
| + | ב. <math>U\cap W = \{0\}</math> | ||
| + | |||
| + | |||
| + | על מנת להוכיח את א, צריך להוכיח את 1+2 שלך (זו סה"כ הכלה דו כיוונית שמוכיחה שיוויון). | ||
| + | |||
| + | ב' הוא בדיוק 3 שלך. | ||
| − | |||
| − | |||
<!------------------------------[שאלות חדשות יש לכתוב בראש הדף, לא בסופו. נא לא לכתוב מתחת לקו זה]------------------------------> | <!------------------------------[שאלות חדשות יש לכתוב בראש הדף, לא בסופו. נא לא לכתוב מתחת לקו זה]------------------------------> | ||
גרסה אחרונה מ־14:44, 15 באוגוסט 2011
תוכן עניינים
- 1 הוראות
- 2 ארכיון
- 3 שאלות
- 4 שאלות
- 4.1 ציונים סופיים
- 4.2 פגישה
- 4.3 שאלה בקשר לפתרון של מועד ב
- 4.4 תרגילים נוספים?
- 4.5 ציוני תרגיל
- 4.6 שאלה 1.ג במבחן
- 4.7 תרגילי בית
- 4.8 בקשר לציוני התרגיל
- 4.9 בקשת הבהרה
- 4.10 ציונים
- 4.11 שאלה
- 4.12 ציון ביניים
- 4.13 ציון מעבר
- 4.14 פקטור
- 4.15 אחוזים
- 4.16 תרגולים 4-5
- 4.17 הערה
- 4.18 פתרונות
- 4.19 ציונים
- 4.20 תגובות לגבי פתרון המבחן
- 4.21 מבחן
- 4.22 שאלה
- 4.23 כמה שאלות לגבי פתרונות המבחן
- 4.24 שאלה אחרונה
- 4.25 שאלה
- 4.26 6.14 עמוד 62 בחוברת
- 4.27 עזרה
- 4.28 שיחלוף
- 4.29 העתקת המטריצה
- 4.30 מושג
- 4.31 שאלה 8 ממבחן 2002 מועד א'
- 4.32 החוברת עמוד 48
- 4.33 שאלה 8 ממבחן 2002 מועד א'
- 4.34 שאלה 1 מקובץ מצורף תרגול 4
- 4.35 שאלה
- 4.36 mod
- 4.37 שאלה
- 4.38 פרטים על המבחן בעמוד הראשי
- 4.39 שאלה/בקשה
- 4.40 שאלה
- 4.41 מבחן תשס"ד מועד ב' חלק אמריקאי שאלה 2
- 4.42 שאלה על הוכחה
- 4.43 שאלה
- 4.44 מטריצות סימטריות ואנטי סימצטריות
- 4.45 מבחן תשס"ד מועד א' חלק אמריקאי שאלה 11
- 4.46 מבחן תשס"ד מועד א' חלק אמריקאי שאלה 9
- 4.47 מבחן תשס"ד מועד א' חלק אמריקאי שאלה 4
- 4.48 מבחן תשס"ד מועד א' חלק אמריקאי שאלה 1
- 4.49 שאלה על מכפלת מטריצת הפיכה והשחלוף שלה
- 4.50 קישורים למבחנים
- 4.51 שאלה
- 4.52 שאלה דחופה
- 4.53 חח"ע ועל של ה"ל
- 4.54 2.15ב'
- 4.55 שאלה
- 4.56 char-ים במבחן
- 4.57 1.28
- 4.58 2.15
- 4.59 מבחן תשסה מועד ב' שאלות אמריקאיות שאלה 10
- 4.60 מבחן תשסה מועד ב' שאלות אמריקאיות שאלה 3
- 4.61 rank
- 4.62 טעות במספר תעודת זהות
- 4.63 שאלה על rank
- 4.64 שאלה ממבחן
- 4.65 שאלה ממבחן
- 4.66 שאלה ממבחן
- 4.67 שיעור חזרה ביום ראשון
- 4.68 עמוד 49 שאלה 11.8
- 4.69 שאלה ממבחן 2005 מועד א
- 4.70 2.11
- 4.71 שאלה ממבחן
- 4.72 2.8
- 4.73 6.14
- 4.74 1.28
- 4.75 כמה שאלות
- 4.76 המבחן
- 4.77 11.10
- 4.78 שאלה 6.14
- 4.79 2.8
- 4.80 2.7
- 4.81 1.28
- 4.82 שאלה (שקשורה ל6.14)
- 4.83 1.14
- 4.84 שאלה
- 4.85 1.28
- 4.86 שאלה
- 4.87 שאלה למתרגלים (או למתרגל הספציפי שלי, אדם צ'פמן
- 4.88 תרגיל 11.8
- 4.89 תרגיל 11.2
- 4.90 בסיס
- 4.91 11.10
- 4.92 שאלה לתשובה
- 4.93 תרגיל 2.8
- 4.94 מרחב עמודות ***עוד שאלה***
- 4.95 תרגיל 11.2ב
- 4.96 סכום ישר
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין
הודעה חשובה !!! - יש להגיש את התרגילים הנוספים (13 , ו 14 כרשות למי שמגיש ) עד ,וכולל , 16.9.2010 ! למשל לתא הבודקת הילה הלוי בכר , או לתומר ביום רביעי או לניר ביום חמישי - בתרגולי החזרה . אנא הודיעו למי שאתם יודעים שלא יגיע לתרגולים אלו . תודה:)
ארכיון
ארכיון 1 - תרגיל 1
ארכיון 2 - תרגיל 2
ארכיון 3 - בוחן + תרגיל 3
ארכיון 4 - תרגיל 3
ארכיון 5 - תרגיל 4
שאלות
שאלות
ציונים סופיים
עוד מעט מתחיל סמס א', מתי יפורסמו הציונים הסופיים?
פגישה
הפגישה היום (י"א תשרי) בקשר לרישום, היא עם הורים?
עוד שאלה, באיזה שעה היא ואיפה?
שאלה בקשר לפתרון של מועד ב
בשאלה 8 א כתבת ש (1,0) != (1,6) אבל אנחנו נמצאים בz3 אז זה לא אומר ש (1,6)=(1,0) ואז הטענה אינה נכונה?
תשובה
נכון! בכלל לא שמתי לב לשאלה. מזל שאני לא נבחנתי על זה. אני אתקן ואעלה מחדש
תרגילים נוספים?
שלום רב, האם היו תרגולים נוספים אשר היינו אמורים להגיש (בחלקו העליון של דף זה נכתב: "הודעה חשובה !!! - יש להגיש את התרגילים הנוספים (13 , ו 14 כרשות למי שמגיש ) עד ,וכולל , 16.9.2010 ! למשל לתא הבודקת הילה הלוי בכר , או לתומר ביום רביעי או לניר ביום חמישי - בתרגולי החזרה . אנא הודיעו למי שאתם יודעים שלא יגיע לתרגולים אלו . תודה:):") או שזו טעות? תדה מראש.
תשובה
זה לא קשור לקורס הזה בשום צורה, הייתה טעות... פה יש 5 תרגילים בלבד
ציוני תרגיל
הגשתי את תרגיל 4 ומופיע כאילו לא הגשתי אותו (מס' ת.ז. 205632516)
שאלה 1.ג במבחן
האם כדי להוכיח סכום ישר, לא צריך להוכיח גם סכום ז"א ש- U+W=V.
תשובה
ברור שכן, שכחתי להוסיף את זה. אני אעלה עוד כמה דקות תוספת לפתרון.
- העלאתי את התוספת הדרושה. --ארז שיינר 22:52, 13 בספטמבר 2010 (IST)
תרגילי בית
היכן ניתן למצוא תרגילי בית שלא קיבלתי חזרה?
- לא ניתן למצוא אותם בשלב זה.
בקשר לציוני התרגיל
אנחנו נקבל את הציונים של תרגילים 4 ו5? עברו כבר שבועיים והמבחן..
אני צריך לדעת בשביל להחליט אם לעשות מועד ב'.
תשובה
הנה רשימת הציונים שיש בינתיים ציוני תרגיל 1-4
בקשת הבהרה
למה כוונתכם באמירה "הבוחן יהיה ציון מגן בלבד": 1. אם הוא גבוה משיעורי הבית אז הוא יהיה במקומם. 2. אם הוא גבוה מהמבחן אז החלוקה תהיה 80% מבחן, 10% בוחן, 10% שיעורים. 3. אם הוא גבוה מהשיעורים אז החלוקה תהיה 80% מבחן, 10% בוחן, 10% שיעורים. 4. אחר?
תודה, גל.
תשובה
מתוך ציון התרגיל בלבד הוא מגן. כלומר המבחן 80 אחוז בכל מקרה (אמנם זה כמו שרשמת, אבל רשמת רק אופציה אחת).
אם הוא גבוה משיעורי הבית זה יהיה 10 אחוז 10 אחוז, ואם נמוך זה יהיה 20 אחוז שיעורי בית.
תשובה לתשובה
תודה רבה על התשובה המהירה. כרגע רשום באתר המידע האישי שהמבחן 85%, אני מניח שזה יתעדכן? ומתי נקבל את ציוני תרגול 4-5 ואת השקלול הסופי של הציונים בתרגולים? שוב תודה, גל.
- זה מוזר שרשום שם 85... או שזה יתעדכן או שזה ישאר ככה. אני לא חושב שזה הפרש משמעותי במיוחד. תקבלו את שאר הציונים כאשר אני אקבל אותם.
ציונים
מתי יפרסמו את הציון הסופי או את הרכב הציון (אחוזים לכל דבר)? זה יכול להשפיע בהחלטה האם לגשת למועד ב'. אשמח לתשובה מהירה.
שאלה
- האתר לא פועל בחגים, ואני עוד לא ראיתי את הציון שלי, יש דרך כלשהי לראות את הציונים שלי?
- ועוד משהו, הציונים שעלו, הם רק בלינארית, או שזה גם בבדידה? תודה רבה, ושנה טובה לכולם!
ציון ביניים
מה זה אומר בדיוק? וכמה עולה לצפות במחברות הבחינה? תודה. (אגב, ציוני הביניים עלו!!)
- ציון ביניים = חלקי הציון הכללי לפני מעבר שקלול. הציון הסופי יעלה רק לאחר שיעלו כל ציוני הביניים.
- עלות צפייה במחברת בחינה 5 ש"ח דרך כ"א. אפשר לצפות בה דרך האתר, אפשר גם להוריד אותה (ע"י לחיצה על כפתור השמירה תוך כדי הצפייה במחברת). (אינני מתרגל)
ציון מעבר
הודיעו מתישהו מה הציון הכללי שצריך כדי לעבור? בכל מקרה, מה הציון?
- באופן כללי באוניברסיטה ציון מבחן עובר הוא 60 ארז שיינר 21:44, 7 בספטמבר 2010 (IDT)
- מה זה אומר שהציון עובר, או נכשל - במבחן? מה, אי אפשר לעבור את הקורס עם נכשל במבחן?
- התכוונתי לציון סופי, לא ציון מבחן. ציון סופי 60 זה עובר (אחרי השקלול של ציון התרגיל). ארז שיינר 23:10, 7 בספטמבר 2010 (IDT)
- מה זה אומר שהציון עובר, או נכשל - במבחן? מה, אי אפשר לעבור את הקורס עם נכשל במבחן?
פקטור
היה במבחן בלינארית פקטור? אם כן, כמה?
אחוזים
בתחילת הסמסטר אמרו לנו שהציון מורכב מ: 80% מבחן, 10% בוחן, 10% ש.ב.. רציתי לדעת האם יש שינוי בהרכב הציון?
- לא בטוח. אתם תראו את הציון הסופי כאשר הוא יופיע
תרגולים 4-5
האם תעלו את הציונים שלהם בהמשך? תודה מראש.
- כן, כאשר הם יתקבלו
הערה
קודם כל אני רוצה להגיד תודה על כל העזרה עם השאלות באלגברה לינארית. אני יודע שזאת בקשה גדולה ואתם לא חייבים להיענות לה, אך המתרגלים שעד עכשיו ענו על תשובות לאלגברה לינארית, יכולים לעזור גם בבדידה? כי נראה לי שאף אחד לא נכנס לדף של בדידה... תודה רבה!!
פתרונות
איפה מופיעים הפתרונות של המבחן???
ציונים
איפה יופיעו הציונים?
- ומתי?
- לפי מה שידוע לי - בעוד כשבוע. אבל אשמח לתשובה ממרצה/מתרגל.
תגובות לגבי פתרון המבחן
תיקונים:
את שאלה 1 ו-4 לא עשיתי ככה שלא התייחסתי אליהם, בשאלה 2, הצבת את 1 במקום a ועדיין השארת a בפיתרון הכללי.. (ובמטריצה) בשאלות האמריקאיות- היה צריך להוכיח ולהפריך או רק לרשום כן/לא? תוכל בבקשה להעלות את ההגדרות, כי יש כמה גרסאות ורציתי לדעת אם יש הבדל, למשל: KerT= מרחב הפתרונות של המערכת Ax=0 כאשר A מטריצה מייצגת העתקה T, נקרא הגרעין של ההעתקה T. (KerT) / מרחב הוקטורים שההעתקה T שולחת אותם ל-0. סה"כ את שתיהן המרצה כתב לנו ושתיהן הגדרות פורמליות..
תשובה
צודק לגבי ההצבות, באמת טעות טפשית.
לא היה צריך להוכיח או להפריך, אבל אחת המטרות העיקריות של התשובות היא שמי שצריך יוכל ללמוד מהפתרון למועד ב'. (וכמובן גם מי שלא ייגש - טוב שיידע את התשובות הנכונות).
לגבי ההגדרות, אני לא יודע מה המרצים יקבלו.
מבחן
בשאלה 3 ג' בתשובות, בשלב שלפני שמתקבלת המטריצה הסופית (כפל שתי מטריצות), במטריצה השמאלית, במקום 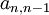 , אני חושבת שאמור להיות
, אני חושבת שאמור להיות 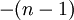 ולא
ולא 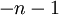 . נכון?
. נכון?
- כן, תודה.
שאלה
אם כתבתי בשאלה 2 ב' שאין בסיס וליד זה את האות פי, זה בסדר? כי אני יודע שהבסיס הוא פי, אבל כתבתי לפני זה שאין בסיס, תודה רבה
- (לא מתרגלת) פי? מה הקשר של פי לקבוצה ריקה?
- הכוונה היא לאות
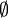 , המסמנת את הקבוצה הריקה. עוזי ו. 22:01, 31 באוגוסט 2010 (IDT)
, המסמנת את הקבוצה הריקה. עוזי ו. 22:01, 31 באוגוסט 2010 (IDT)
- הכוונה היא לאות
- תחליט: או שאין בסיס, או שיש בסיס והוא הקבוצה הריקה. האפשרות הראשונה בוודאי אינה נכונה, משום שלכל מרחב וקטורי יש בסיס (את המקרה הסופי הוכחתם בקורס; המקרה הכללי הוא משפט של Hammel). הקבוצה הריקה היא הבסיס (היחיד) של מרחב האפס. עוזי ו. 22:01, 31 באוגוסט 2010 (IDT)
- אני כתבתי שאין בסיס וליד זה את האות
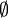 , כל החישובים שלי בתרגים נכונים וגם על פי התשובות שלכם אין לי טעות אחת במבחן, הדבר היחיד שלא היה טוב זה שאחרי שהגעתי לזה שהחיתוך הוא 0 כתבתי שאין בסיס, וליד זה
, כל החישובים שלי בתרגים נכונים וגם על פי התשובות שלכם אין לי טעות אחת במבחן, הדבר היחיד שלא היה טוב זה שאחרי שהגעתי לזה שהחיתוך הוא 0 כתבתי שאין בסיס, וליד זה 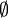 , יורידו על זה הרבה נקודות? כי זה לא שהיה לי טעות אחרת חוץ מזה, וגם כתבתי
, יורידו על זה הרבה נקודות? כי זה לא שהיה לי טעות אחרת חוץ מזה, וגם כתבתי 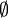 בפתרון הסופי, תודה
בפתרון הסופי, תודה
- יורידו אולי נקודות, אני לא יודע מראש כמה. אם אין לך טעויות חוץ מזה יהיה לך ציון טוב. ארז שיינר 12:09, 1 בספטמבר 2010 (IDT)
- אני כתבתי שאין בסיס וליד זה את האות
כמה שאלות לגבי פתרונות המבחן
1. בשאלה 3א האם אפשר היה להוכיח את היותה של הקבוצה בסיס על ידי שימוש בכך ש:
א. 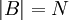 ולכן משום היותה בסיס
ולכן משום היותה בסיס 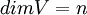 ומשום
ומשום 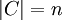 עפ"י הגדרתו אז
עפ"י הגדרתו אז 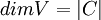 .
.
ב. בת"ל (וגם לא הוכחתי כפי שאתם הוכחתם אלא הוכחתי בשלילה, אמנם יצא לי יותר ארוך אבל אני מניח שזה בסדר, לא?!?).
2. ב-3ב לא יותר קצר למצוא את המטריצה הנדרשת באותו אופן שאתם מצאתם את ההופכית שלה?
3. בפתרון ל-2א יש לך טעות: הצבת a=1 וללכן לא יכול להיות שהפתרון הכללי למקרה של אינסוף פתרומנות תלוי ב-a.
4. איך נעשית חלוקת הנקודות בין הסעיפים בין השאלות הפתוחות? לכל סעיף משקל שווה?
תודה מראש ושנה טובה!
תשובה
1. בת"ל ובגודל n + השלישי חינם זה סבבה.
2. אפשרי, קצר זה עניין של דעה :)
3. כן, העירו לי על כך. תודה. כמובן שצריך להציב בכל מקום שם את a ולא רק בחלק מהמקומות :)
4. לא ידוע, יוחלט בעת הבדיקה.
שנה טובה ומבורכת.
שאלה אחרונה
למה אם rankAB < min{rankA,rankB} אז A וגם B אינן הפיכות? תודה!
תשובה
כי אם A או B הפיכות, אז AB היא בעצם A או B שמבצעים עליה פעולות אלמנטריות, עשיית פעולות אלה לא משנות את מרחב השורות ובטח לא את מימדו, ואז המימד של מרחב השורות של AB היה שווה למימד המינימלי בין A ו-B ולא קטן ממש.
- תודה רבה על התשובה בשעה מוקדמת! אשמח אם תוכל לענות לי על השאלה השניה לפני המבחן! תודה!
שאלה
במבחן 2003 מועד ב' שאלה 1 (צריך למצוא את [v]c, יש טעות בתשובה? עשיתי כמה פעמים מכל הכיוונים ויצא לי תשובה 4 ולא 2. תודה!
6.14 עמוד 62 בחוברת
בתשובות שבאתר הוספת לבסיס את (1,0,0). למה, לפי מה?
- מדרגים ומוסיפים את e_i עבור כל העמודות i של המשתנים החופשיים (כלומר משלימים איברים פותחים)
- אהה.. באמת? חידשת לי. תמיד כשרוצים להשלים קבוצה בת"ל לקבוצה פורשת אז שמים את הוקטורים מהקבוצה הבת"ל בשורות מטריצה, מדרגים, ורואים אילו משתנים חופשיים יש. לאחר מכן מוסיפים קבוצה ובה וקטורים
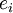 , עבור כל עמודה i שבה יש משתנים חופשיים? יש איזה משפט קשור או משהו שמסביר למה עושים דווקא ככה? תודה.
, עבור כל עמודה i שבה יש משתנים חופשיים? יש איזה משפט קשור או משהו שמסביר למה עושים דווקא ככה? תודה.
- אהה.. באמת? חידשת לי. תמיד כשרוצים להשלים קבוצה בת"ל לקבוצה פורשת אז שמים את הוקטורים מהקבוצה הבת"ל בשורות מטריצה, מדרגים, ורואים אילו משתנים חופשיים יש. לאחר מכן מוסיפים קבוצה ובה וקטורים
- זה פשוט מאד, כמו שאמרתי - משלימים את האיברים הפותחים. לאחר התוספת יש n איברים פותחים (אם יש n עמודות) ואז מרחב השורות הוא ממימד n ובהכרח מרחב השורות הוא כל F^n.
עזרה
איך מוכיחים את המשפט: יהי בסיס v1,..,vn לV וקבוצה w1,..wn בW, אז יש העתקה לינארית כך ש T(vi(=Wi? תודה!
תשובה
לא יודע איך הוכיחו לכם בכיתה (כנראה אחרת) אבל אפשר עם המטריצה המייצגת. כלומר למצוא את המטריצה המייצגת לפי ההגדרה נקרא לה A ואז ההעתקה Tx=Ax היא העתקה לינארית שמקיימת את הדרישה.
- המטריצה המייצגת הוגדרה בהתבסס על המשפט הזה ולכן אני לא חושב שמותר להשתמש בה (אני לא מתרגל).
שיחלוף
במשוואה שכוללת מטריצות, מותר לשחלף את שני האגפים וזה ישמור על שיוויון, בלי להסביר או להוכיח (אם זה לא התרגיל), נכון?
- אתה מתכוון ש-
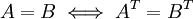 ? בטח שזה נכון. זו בדיוק אותה מטריצה, ופעולת השיחלוף מוגדרת היטב (חד-ערכית). אני לא מתרגל, אבל אני כמעט בטוח שלא צריך להסביר או להוכיח.
? בטח שזה נכון. זו בדיוק אותה מטריצה, ופעולת השיחלוף מוגדרת היטב (חד-ערכית). אני לא מתרגל, אבל אני כמעט בטוח שלא צריך להסביר או להוכיח.
העתקת המטריצה
בחוברת עמוד 52 שאלה 1.10 ב' - או שלא הבנתי את ההגדרה, או שיש טעות בהגדרת הטווח של ההעתקות T,S. למשל עבור העתקה T: הרי כפל של מטריצה מסדר m על n בוקטור מסדר n על 1 נותן וקטור מסדר m על 1 ולא הפוך!
ועוד דבר - צריך לזכור בעל פה את ההגדרות של העתקת המטריצה, ההעתקות  ,
,  ועוד? אם לא, אז אילו הגדרות של העתקות כן צריך לזכור בעל פה?
ועוד? אם לא, אז אילו הגדרות של העתקות כן צריך לזכור בעל פה?
תשובה
אתה צודק זה באמת צריך להיות הפוך.
לא בטוח למה אתה מתכוון, אלה דברים שלמדתם בהרצאה, תלוי מה המרצה אמר שצריך לזכור.
מושג
מה זה "מרחב האפס"?
- קבוצה שהאיבר היחיד בה הוא 0, והקבוצה הזאת היא מרחב וקטורי כל התנאים של מרחב וקטורי מתקיימים.
- תודה. בעמוד 50 שאלה 11.15 ד' (בחוברת), אומרים "מצא בסיס למרחב האפס של A". מה הכוונה?
הכוונה היא שתמצא בסיס למרחב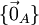 , כלומר המרחב שכולל את האיבר הנייטרלי לחיבור ב-A.
, כלומר המרחב שכולל את האיבר הנייטרלי לחיבור ב-A.
- תודה. בעמוד 50 שאלה 11.15 ד' (בחוברת), אומרים "מצא בסיס למרחב האפס של A". מה הכוונה?
תשובה
מרחב האפס בלי הקשר הוא אכן המרחב שמכיל בלבד את אפס. מרחב האפס של מטריצה, בד"כ, הוא מרחב הפתרונות של המערכת ההומוגנית.
- תודה!
שאלה 8 ממבחן 2002 מועד א'
למה סכום איברי המטריצה הוא 1?? מאיפה בתשובות הוא הביא את התשיעית הזאת? המטריצה P היא 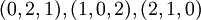 ולכן סכום איברי המטריצה הוא 0+2+1+1+0+2+2+1+0=9, למה 1?? תודה!
ולכן סכום איברי המטריצה הוא 0+2+1+1+0+2+2+1+0=9, למה 1?? תודה!
תשובה
אתה רשמת את מטריצת המעבר מB לC. אבל P היא ההופכית שלה, מטריצת המעבר מC לB.
- וואלה, תודה..
החוברת עמוד 48
כתוב שם שמרחב העמודות הוא תת מרחב של 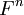 כאשר
כאשר  מסדר
מסדר 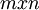 ואני חושבת שמרחב העמודות הוא תת מרחב של
ואני חושבת שמרחב העמודות הוא תת מרחב של 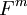 . לא? (כנ"ל לגבי מרחב השורות, רק הפוך)
. לא? (כנ"ל לגבי מרחב השורות, רק הפוך)
- נכון זו טעות בחוברת.
שאלה 8 ממבחן 2002 מועד א'
איך ניגשים לשאלה כזאת? מה הקשר בין הפיכות של הפונקציה לRANK שלה? אפשר הסבר מפורט בבקשה? זה ממש מבלבל! וגם, למה נתונה מטריצה B אם היא נמצאת בשאלה בכלל? תודה רבה מראש
תשובה
יש כמה קשרים בין השניים. למשל הrank של מטריצה ריבועית מגודל n שווה לn אם"ם היא הפיכה. אם נסתכל על זה בתור העתקות ליאריות, אז הrank הוא מימד התמונה והוא קטן ככל שמימד הגרעין גדל.
- למה אני אמור להסיק שA אינה הפיכה ב3?
- אם תסתכל על המשפט שרשמתי אז תראה שA הפיכה אם"ם הrank שלה הוא n אם הrank של A^2 קטן מהrank של A בוודאי הוא קטן מn ולא יכול להיות שהיא הפיכה. אבל אם A הפיכה בוודאי A^2 הייתה צריכה להיות הפיכה.
שאלה 1 מקובץ מצורף תרגול 4
שלום רב. בשאלה התבקשנו להוכיח ש- ![[I]_C^B](/images/math/0/3/a/03ab7b30c95f95155684b42997329afe.png) הפיכה. האם לא מספיק פשוט לומר ש-
הפיכה. האם לא מספיק פשוט לומר ש- ![([I]_C^B)^{-1}=[I]_B^C](/images/math/7/4/6/746dd537cd9e4c42a19773f235f5e152.png) ע"י בדיקה שאכן מתקיים שמכפלתן משני הצדדים היא
ע"י בדיקה שאכן מתקיים שמכפלתן משני הצדדים היא 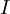 תודה, גל.
תודה, גל.
תשובה
אפשר, אם ידוע המשפט שקיימת מטריצת מעבר בין כל שני בסיסים ואז להשתמש בנוסחא של מטריצת מעבר.
- כלומר שאם מבקשים ממני במהלך המבחן להוכיח את זה אסור לי להשתמש במה שאמרתי?
- תלוי מה יבקשו ספציפי. אם השאלה הייתה מופיעה כמו שהיא במבחן זה היה בסדר. תשאל בזמן המבחן.
שאלה
אם v מוכל בw וגם dim של v שווה לdim של w אזי v=w זה משפט? וכיצד ניתן להוכיח?
תשובה
שאלה 7.7 תרגיל 4.
לא ענית לי על שתי השאלות: זה משפט? איך מוכיחים?
זה עובדה, ומוכיחים כמו בפתרונות שיש באתר כמובן.
אפשר להשתמש בזה אלא אם צריך להוכיח את זה במפורש.
mod
המספר -1 בZ5 כלומר 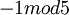 זה 1 או 4? תודה!
זה 1 או 4? תודה!
תשובה
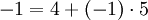 ולכן זה 4.
ולכן זה 4.
שאלה
למה אם למערכת הומוגנית Ax=0 יש פתרון יחיד, אזי A הפיכה? תודה!
תשובה
קודם כל זה נכון רק אם A ריבועית. יש כמה וכמה הוכחות, למשל מטריצה ריבועית שקולת שורה למטריצת היחידה אם"ם היא הפיכה, ואם הצורה הקנונית של מטריצה ריבועית היא לא מטריצת היחידה סימן שיש לה משתנים חופשיים ולכן יותר מפתרון אחד.
דרך אחרת להסתכל על זה היא שעמודות A בת"ל אם"ם למערכת Ax=0 יש פתרון יחיד, וידוע שעמודות מטריצה ריבועית בת"ל אם"ם היא הפיכה.
- תודה!
פרטים על המבחן בעמוד הראשי
פרטים על המבחן בעמוד הראשי
- מה לגבי כמה זמן המבחן ומה המבנה שלו?
- כבר אמרו את זה בהרצאות.
- ומי שלא הקשיב או לא היה מרוכז? או לא היה בשיעור?
- שישאל את החברים שלו. שאלות לגבי המבחן צריכות להיות מופנות למרצים ולא למתרגלים.
- ומי שלא הקשיב או לא היה מרוכז? או לא היה בשיעור?
- כבר אמרו את זה בהרצאות.
שאלה קטנה
איפה זה בניין 507? זה הבניין שאנחנו בדרך כלל לומדים בו או בניין אחר? תודה!
- אנחנו לומדים ב-604.
- אז אפשר הכוונה לגבי איפה זה 507?
- 507 זה הבניין הגדול עם המבנה המיוחד והמגני דויד למעלה, ממש ליד הבניין שאתם לומדים בו.
- אז אפשר הכוונה לגבי איפה זה 507?
שאלה/בקשה
נכון יש משפט שאומר (אני לא יודע ממש איך לכתוב בשפה המתמטית בפורום, לכן הבינו ש2 אותיות אחרי הT פירושן שהאות הראשונה למעלה מימין והשנייה למטה מימין וכו'): ![[T]FG=[Iw]HG[T]EH[Iv]FE](/images/math/8/b/f/8bf4d310298f5cc7e8d14ae009c8e465.png) ? אז השאלה שלי היא, למה צריך את המשפט הזה תכלס? מתי המשפט הזה עוזר? והאם מתרגל יכול, בבקשה, להביא תרגיל אחד שבו חייבים/ רצוי מאוד להשתמש במשפט הזה? תודה רבה!
? אז השאלה שלי היא, למה צריך את המשפט הזה תכלס? מתי המשפט הזה עוזר? והאם מתרגל יכול, בבקשה, להביא תרגיל אחד שבו חייבים/ רצוי מאוד להשתמש במשפט הזה? תודה רבה!
תשובה
![[T]_G^F=[Iw]_G^H[T]_H^E[Iv]_E^F](/images/math/2/6/4/2643a5dfa8133d40863a7a1ce0ad7f33.png)
השתמשנו בנוסחא הזו בשאלה הקודמת שלך... פשוט שם הייתה גם המטריצה ![[I]_S^S](/images/math/4/e/e/4ee200c344ec5f920a71ec5118d8e6e8.png) שהיא שווה למטריצת היחידה ולכן לא הזכרנו אותה.
שהיא שווה למטריצת היחידה ולכן לא הזכרנו אותה.
שאלה
מבחן 2004 מועד א' שאלה אמריקאית 3.. איך מוצאים את המימדים של U ו W?
- (אני לא מתרגל)- 2 הSPANים פורשים, רק תבדוק אם יש בכל אחד מהSPANים איברים שתלויים אחד בשני, אם יש- תוריד אותם, ותישאר עם בסיסים לU וW.
תשובה
מעבירים לצורה וקטורית שמים בשורות מטריצה ומדרגים.
מבחן תשס"ד מועד ב' חלק אמריקאי שאלה 2
התשובה לא אמורה להיות A^-1*B במקום B*A^-1? כי ![[T]AB=[I]SB*[T]AS=(A^-1)*B](/images/math/6/b/0/6b0a2b2be3372b864cd0e4c410088699.png) לא? תודה!
לא? תודה!
תשובה
לא נתון שB הוא בסיס בכלל. [T] צריכה לקיים את המשוואה ![[T][v]=[Tv]](/images/math/c/6/8/c6805daa449e0209f6b1562c08ab372e.png) . לכן
. לכן ![[T][v_i]=[T]v_i=[Tv_i]=w_i](/images/math/5/9/1/591cdc5f7cde30f4e5a4aee340034393.png) (כי הקואורדינטות לפי הבסיס הסטנדרטי שוות לוקטור עצמו). אבל
(כי הקואורדינטות לפי הבסיס הסטנדרטי שוות לוקטור עצמו). אבל 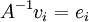 ואז
ואז 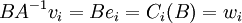 כפי שרצינו.
כפי שרצינו.
דרך אחרת להוכיח: (פשוט הרבה יותר)
![[T]=[T]_S^S=[T]_S^A\cdot [I]_A^S=BA^{-1}](/images/math/9/2/7/9273746fd79d92336f40b0f256f05546.png)
שאלה על הוכחה
האם ההוכחה הזאת קבילה?: נתון ש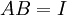 וכי
וכי 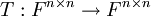 כך ש:
כך ש: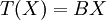 , אני צריך להוכיח ש
, אני צריך להוכיח ש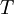 על:
"נניח -T לא על: לכן קיים
על:
"נניח -T לא על: לכן קיים 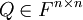 כך שלכל
כך שלכל 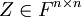
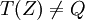 לכן
לכן 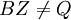 לכן
לכן 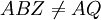 כלומר-
כלומר- 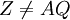 בסטירה לכך שהטענה נכונה עבור כל
בסטירה לכך שהטענה נכונה עבור כל 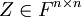 לכן T על? האם זה נכון?
לכן T על? האם זה נכון?
תשובה
כן, עדיף הוכחות כאלה לבצע בחיוב ולא בשלילה. תהי Q מטריצה כלשהיא, אזי המקור שלה הוא AQ ולהוכיח את זה.
כן אבל בתרגיל הספציפי הזה אסור היה להשתמש במשפט שהיה נתון רק ש
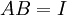
שאלה
מבחן 2 שאלה אמריקאית 2.. הטענה חייבת להיות לכל Im(z)==0 אחרת זה לא יכול להתקיים
- מה זה מבחן 2? איזו שנה? איזה מועד?
- 2005 מועד א'
- נראה לי שאתה צודק... יהי
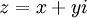 ולכן
ולכן 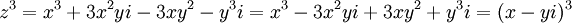 נפשט ונקבל ש-
נפשט ונקבל ש- 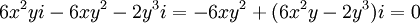 . לאחר השוואה אני קיבלתי שאמנם ישנם אינסוף מקרים אבל בכולם
. לאחר השוואה אני קיבלתי שאמנם ישנם אינסוף מקרים אבל בכולם 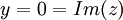
- נראה לי שאתה צודק... יהי
- 2005 מועד א'
תשובה
מטריצות סימטריות ואנטי סימצטריות
שאלה: אם  ו-
ו- סימטריות (שתיהן ריבועיות מאותו גודל) אז: האם
סימטריות (שתיהן ריבועיות מאותו גודל) אז: האם  סימטרית?
חשבתי על לפתור בדרך הזו: לפי סימטריות מתקיים ש:
סימטרית?
חשבתי על לפתור בדרך הזו: לפי סימטריות מתקיים ש: 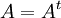 וגם
וגם 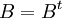 ולכן
ולכן  . אי לכך גם
. אי לכך גם  סימטרית. עם זאת, במבחן של 2003 (מועד א), זוהי שאלה 8 בחלק של האמריקאיות. אם מה שאני אומר נכון הרי שהתשובה אמורה להיות 3, אבל באתר כתוב שהתשובה היא 1. מה הטעות שלי? תודה, גל.
סימטרית. עם זאת, במבחן של 2003 (מועד א), זוהי שאלה 8 בחלק של האמריקאיות. אם מה שאני אומר נכון הרי שהתשובה אמורה להיות 3, אבל באתר כתוב שהתשובה היא 1. מה הטעות שלי? תודה, גל.
תשובה
אתה צודק, ABA סימטרית אם A,B סימטריות מאותו גודל
מבחן תשס"ד מועד א' חלק אמריקאי שאלה 11
איך פותרים שאלה כזאת? הצלחתי להבין ש
![[T]B=(u1,u2,u3;0,0,0;w1,w2,w3)](/images/math/f/6/f/f6f4f2e023a5d2ae84a838b5c857bae9.png) (; מפריד בין עמודות)
אבל איך יודעים איפה יש עוד אפסים? אם התשובה היא 2 או 4? תודה רבה!
(; מפריד בין עמודות)
אבל איך יודעים איפה יש עוד אפסים? אם התשובה היא 2 או 4? תודה רבה!
תשובה
אני לא מתרגל אבל נראה לי שאני יכול לרמוז לך- תסתכל על הבסיס של האימג'- כל איבר בתמונה אתה יכול להציד כצירוף ליניארי שלהם.
- לא הייתי עולה זה בחיים, אבל הבנתי- תודה רבה!
מבחן תשס"ד מועד א' חלק אמריקאי שאלה 9
למה התשובה הנכונה היא- כל התשובות לא נכונות? אני זוכר שלמדנו משפטון שאומר שאם v1,..vk בת"ל אזי Tv1,..Tvk בתל כלומר 3 היא התשובה הנכונה.. לא? תודה!
תשובה
המשפטון שאתה מזכיר מחייב T חח"ע. למשל העתקת האפס תהווה דוגמא נגדית לסעיף זה
מבחן תשס"ד מועד א' חלק אמריקאי שאלה 4
הצלחתי להבין, בשיטת האלימנציה, שהתשובה היא T32=0, אבל אני ממש לא יודע בדיוק למה, אפשר בבקשה הסבר קצר על למה אפשר לדעת בוודאות שT32=0 ואיך אפשר להוכיח את זה? תודה!
תשובה
נבנה בסיס לגרעין של ההעתקה. הגרעין של T^2 בהכרח גדול ממש מהגרעין של T אחרת ההעתקה תתקע על אותו מצב ולא תתאפס בחיים (אבל נתון שהיא מתאפסת). ולכן מימד הגרעין גדול ב1 לפחות. אחרי 32 צעדים כאלה נגיע לגרעין בגודל 32 - כלומר העתקת האפס.
מדוע ההעתקה תתקע? אני אשאיר את זה כתרגיל.
- למה גרעין בגודל 32 הוא העתקת האפס? כי המימד הוא 32?
- וזה נכון לומר שהגרעין של TT חייב להיות גדול ממש מהגרעין שלT כי אם היה להם אותו מספר של איברים בגרעין אז מה שמאפס את T^1024 מאפס גם את T^1023 ואז זה אומר ש T^1023 הוא העתקת האפס, וככה עד שמגיעים ל-שT היא העתקת האפס תמיד, אבל יודעים שהיא לא העתקת האפס תמיד? תודה
- קודם כל כן, אם הגרעין בגודל 32 אז הוא כל המרחב ולכן זו העתקת האפס.
- שנית, לא זו לא הוכחה נכונה. צריך להוכיח שאם נשלים את הבסיס של הגרעין של T^n לבסיס למרחב כולו, אזי הוקטורים שהשלמנו מהווים גם בסיס לתמונה של T^{n+1} ואז ברור שההעתקה חוזרת על עצמה. לא בטוח שזו הוכחה כל כך פשוטה.
מבחן תשס"ד מועד א' חלק אמריקאי שאלה 1
כל מה שאני יודע הוא שהאפסיות של T היא לפחות 1 כי בטוח שV שהוא לא וקטור האפס נמצא בגרעין, וגם ש TT=0 ולכן לכל u מתקיים T(Tu)=0 ולכן התמונה מוכלת בגרעין ולכן dim(ImT)<=dim(KerT). אבל כל מה שזה נותן לי זה שהמימד של V הוא לא אפס! אפשר עזרה? תודה רבה!
תשובה
המימד הוא בטוח לא 4 כי 4 זה המימד של כל ההעתקות הלינאריות, והקבוצה הזו לא מכילה את כולם. המימד הוא גם לא אפס, יש יש העתקות שונות מאפס כאלה.
נותר לבחור בין 1 לבין 2. נשלים את v לבסיס בעזרת u. אם ההעתקה שונה מאפס, u חייב להשלח לסקלר כפול v (אחרת פעם שנייה שנפעיל את ההעתקה היא לא תתאפס, ישאר שם גורם עם u.) לכן כל שתי העתקות יהיו ת"ל על ידי איפוס הסקלר הזה, ולכן המימד הוא אחד.
- תודה רבה, רק עוד שאלה קטנה, איך יודעים שהמימד של כל ההעתקות הוא 4? תודה!
- זה משפט שיש איזומורפיזם בין מרחב ההעתקות למרחב המטריצות. ואנחנו יודעים מהו המימד של מרחב המטריצות 2 על 2
- הבנתי, תודה!
- זה משפט שיש איזומורפיזם בין מרחב ההעתקות למרחב המטריצות. ואנחנו יודעים מהו המימד של מרחב המטריצות 2 על 2
שאלה על מכפלת מטריצת הפיכה והשחלוף שלה
טענה: עבור  הפיכה הרי שיתקיים ש-
הפיכה הרי שיתקיים ש-  הפיכה (עפ"י משפט) ולכן
הפיכה (עפ"י משפט) ולכן 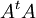 הפיכה כי מכפלת שתי מטריצות הפיכות תתן מטריצה הפיכה נוספת.
השאלה שלי האם זה הסבר מספק לקיום טענה זו. אם לא, מה עליי להוסיף?
ובלי קשר, האם עליי להוסיף הערה מדוע המכפלה
הפיכה כי מכפלת שתי מטריצות הפיכות תתן מטריצה הפיכה נוספת.
השאלה שלי האם זה הסבר מספק לקיום טענה זו. אם לא, מה עליי להוסיף?
ובלי קשר, האם עליי להוסיף הערה מדוע המכפלה 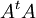 מוגדרת או שזה ברור?
תודה, גל.
מוגדרת או שזה ברור?
תודה, גל.
- בגדול זה בסדר, תלוי מה אתה נדרש להוכיח. בזמן מבחן שואלים את המרצה אם צריך להוכיח כך וכך.
- אוקי תודה. האם יהיו מתרגלים או מרצים כלשהם במבחן (אלי אמר שהוא לא יהיה)? אם כן, איך זה הולך? אתם נכנסים לשאלות או שחייבים לשאול לפני הבחינה?
- יהיה מי שיענה על שאלות בזמן המבחן (על שאלון המבחן ולא רמזים לפתרון כמובן)
קישורים למבחנים
כשעשיתם עריכה לדף של לינארית הוצאתם את הקישורים למבחנים לדוגמא אפשר להחזיר אותם? תודה(:
- זה נמצא בהיסטורית הדף.
- הם פשוט הועברו בטעות לבדידה במקום ללינארית. הם הוחזרו למקום בדף של לינארית
שאלה
האם נושא הדטרמיננטות כלול בחומר למבחן?
אני לא מתרגל, אבל ודאי שלא
שאלה דחופה
מחר צריך לבוא בזמן של ההרצאה (9) או בזמן של התרגול (13:00)? תודה רבה!
- לא יודע מתי המרצים יגיעו. המתרגלים בגדול אמורים לבוא בזמן התרגול הרגיל.
- לפי מה שידוע לי אצלנו (אלי) מתחילים ב-0900.
מי שלומד עם אפי מתי צריך להגיע?? לפי מה שזכור לי הוא אמר שהוא לא יבוא.. אנחנו צריכים לבוא ב9 או ב1?
- אז כנראה שמי שלומד עם אפי צריך להגיע ב1, כי שיעור החזרה שלנו היה ביום שישי, ומחר יהיה לנו רק שיעור חזרה עם המתרגלים ב1..
חח"ע ועל של ה"ל
שלום רב,
נניח ונתונה לי ה"ל 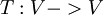 . האם נכון לומר ש
. האם נכון לומר ש  חח"ע אם"ם
חח"ע אם"ם 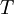 על? ואם כן, האם עליי להסביר במבחן מדוע?
על? ואם כן, האם עליי להסביר במבחן מדוע?
תודה, גל.
תשובה
זה נכון ונובע ממשפט הדרגה V=dimKer+dimIm (צריך לצטט את המשפט ולהסביר למה זה נובע)
למעשה הטענה היא יותר כללית. תהי T:V->W כך שהמימדים של V,W שווים, אזי T על אם"ם T חח"ע.
2.15ב'
אם אני רוצה למצוא את kerTa אז מה שצריך לעשות זה לכפול את המטריצה A במטריצה כללית מסדר 2x2 ולהשוות לאפס- ואז למצוא את המטריצה הכללית?- הכוונה במטריצה כללית זה שאני אסמן a b c d במקום קבועים במטריצה ואז אבדוק מה אני אקבל.. וזה יהיה הker?
- כן, הגרעין זה מה שנשלח לאפס על ידי ההעתקה.
שאלה
אם אני יודע ש: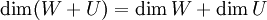 וגם
וגם 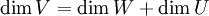 כאשר
כאשר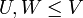 אז אני יכול להגיד ש:
אז אני יכול להגיד ש: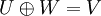 ?
?
תשובה
כן
- (לא אני שאלתי את השאלה) למה כן? אם למשל
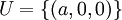 ,
, 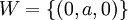 ,
, 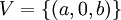 ? (כך ש-a,b שייכים ל-R)
? (כך ש-a,b שייכים ל-R) - ומה ז"א:
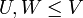 ?
?
- אתה צודק, זה לא נכון (לא אני רשמתי את התשובה הקודמת). אם נוסיף את התנאי ש-
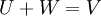 זה כן יהיה נכון.
זה כן יהיה נכון. 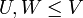 משמעו
משמעו  תת מרחבים של V.
תת מרחבים של V.
- אתה צודק, זה לא נכון (לא אני רשמתי את התשובה הקודמת). אם נוסיף את התנאי ש-
תשובת מתרגל
המשפט נכון, והרי הוכחה:
נתון U,W תתי מרחב של V. אזי ברור ש . לכן לפי הנתון
. לכן לפי הנתון 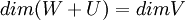 יש לנו תת מרחב עם מימד שווה למרחב ולכן הם שווים
יש לנו תת מרחב עם מימד שווה למרחב ולכן הם שווים 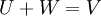 .
.
כעת לפי משפט המימדים 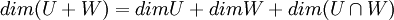 ולכן לפי הנתון
ולכן לפי הנתון 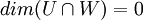 ולכן
ולכן 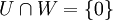 .
.
וזה מה שצריך על מנת להוכיח סכום ישר.
תודה רבה! ואגב לזה שהביא את הדוגמה, בדוגמה שלך W לא תת מרחב של V. אפשר להשתמש בזה או שצריך להוכיח?
- נכון, זה בגלל שלא הבנתי מה אומר סימן ה"קטן-שווה". מצטרפת לשאלה.
- צריך להוכיח.
char-ים במבחן
כמעט לא התעסקנו ב-char-ים בשיעורים, לא תרגלנו והמרצים/מתרגלים בד"כ הזכירו את זה כהערת אגב. יהיו char-ים במבחן? תודה, 16:11, 28 באוגוסט 2010 (IDT)
תשובה
לא יהיה מעבר לדברים דומים למה שעשינו בכיתה.
1.28
לא הבנתי את התרגיל בכלל. את 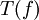 אמנם מצאתי בלי בעיה, אבל איך מוצאים את
אמנם מצאתי בלי בעיה, אבל איך מוצאים את 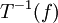 ? קראתי פה שאלה ותשובה:
? קראתי פה שאלה ותשובה:
איך אני מחשב את ההעתקה ההפיכה? יש כמה דרכים. אחת מהן למדתם בהרצאה- בעזרת ההופכית של המטריצה המייצגת. הדרך השנייה היא לפי משפט ההגדרה - מספיק לבחור בסיס בתמונה ולראות מה המקור שלו וכך אפשר לחשב את המטריצה המייצגת של ההעתקה ההופכית.
ולא הבנתי בכלל. מה הקשר למטריצות? (אני יודעת מה זו מטריצה מייצגת, קראתי את הקובץ, וגם במחברת, ונראה לי שהבנתי, אבל מה הקשר לתרגיל הזה? בכלל לא הבנתי מה השימוש של המטריצה המייצגת, מלבד לפתרון של תרגילים מסוג "מצא את מטריצה המייצגת").
ומה זה "בסיס בתמונה", בתרגיל הזה הבסיס הוא 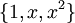 ? את המקור אמצא בעזרת מערכת משוואת כזו:
? את המקור אמצא בעזרת מערכת משוואת כזו: 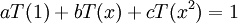 ,
, 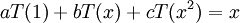 ,
, 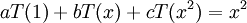 ? ואז.. מה אני עושה עם המקור הזה? שוב, מה קשורה המטריצה המייצגת?
? ואז.. מה אני עושה עם המקור הזה? שוב, מה קשורה המטריצה המייצגת?
תודה רבה מראש, מקווה להסבר מפורט.
ניסיתי עכשיו לפתור איך שראיתי לנכון, בלי מטריצות וכל זה... סימנתי 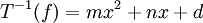 . לאחר מכן אמרתי ש-
. לאחר מכן אמרתי ש-![TT^{-1}(f)=I_{R_2[x]}(f)=f=cx^2+bx+a](/images/math/4/3/7/4373e64eaaa3ccc76eb4a5f7e357c518.png) (ה-
(ה- הוא סימון). מצד שני,
הוא סימון). מצד שני,  וזה שווה למה שמצאתי קודם, הרי יש לי את
וזה שווה למה שמצאתי קודם, הרי יש לי את  . קיבלתי מערכת של 3 משוואות (לפי המקדמים של
. קיבלתי מערכת של 3 משוואות (לפי המקדמים של  ,
,  ,
, 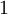 ) ואז ביטאתי את
) ואז ביטאתי את  ,
, ,
, באמצעות
באמצעות  ,
, ,
,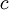 וקיבלתי את
וקיבלתי את 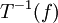 .
.
בלי מטריצות, רק אלגברה. הגיוני? או שבכלל לא הבנתי את התרגיל?
תשובה
- למדנו הרי כיצד למצוא העתקה מפורשת באמצעות מטריצה מייצגת.
- אנחנו יודעים שהתמונה היא מרחב וקטורי, ולכן יש לה בסיס נסמן אותו
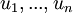
- נמצא w_i כך ש
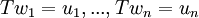
- לכן
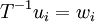 וכך אפשר למצוא את ההעתקה בצורה מפורשת כמו בתרגיל.
וכך אפשר למצוא את ההעתקה בצורה מפורשת כמו בתרגיל.
דרך שנייה:
- נמצא את המטריצה המייצגת של T
- נהפוך אותה על מנת לקבל מטריצה מייצגת של
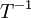
- נמצא את ההעתקה במפורש מתוך המטריצה המייצגת, כמו בתרגיל.
תשובה לתשובה
תודה רבה על התשובה!
לגבי הדרך הראשונה:
- מה זה אומר העתקה מפורשת?
- האם לכל
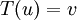 , מתקיים
, מתקיים 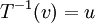 ?
? - תודה, הצלחתי לפתור את התרגיל בדרך הזו! והתשובה יצאה לי כמו זו שיצאה בדרך שעשיתי קודם (זו שפירטתי למעלה). מעניין איזו קצרה יותר או עדיפה מאיזושהי סיבה. יש העדפה כלשהי באופן כללי, ובמבחן בפרט?
לגבי הדרך השנייה:
- המטריצה המייצגת של
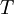 שהיא במקרה הזה פשוט מטריצה
שהיא במקרה הזה פשוט מטריצה ![[T]_S^S](/images/math/8/8/2/8829be5dc91eaff44b495a7234be6b3b.png) כאשר
כאשר  הבסיס הסטנדרטי של
הבסיס הסטנדרטי של ![R_2[x]](/images/math/c/d/d/cdd846d7f5270c4fa600e24b4cfd8f10.png) , בעצם מטריצה שעמודותיה הן (1,0,0), (0,2,3), (0,3,0) - כלומר הצורה הוקטורית של התמונות המתקבלות עבור מקורות מאיברי הבסיס. נכון?
, בעצם מטריצה שעמודותיה הן (1,0,0), (0,2,3), (0,3,0) - כלומר הצורה הוקטורית של התמונות המתקבלות עבור מקורות מאיברי הבסיס. נכון? - ישנו משפט שאומר שהמטריצה ההופכית של המטריצה המייצגת של
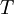 היא המטריצה המייצגת של
היא המטריצה המייצגת של 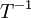 ? (זה קל להוכחה אבל האם צריך להוכיח בכל פעם?)
? (זה קל להוכחה אבל האם צריך להוכיח בכל פעם?) - איך מוצאים את ההעתקה במפורש מתוך המטריצה המייצגת? ואיזה תרגיל?
תשובה
- צורה בה אתה יודע לאין איבר כללי הולך. לדוגמא:
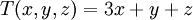
- כן, זו כמעט ההגדרה של ההעתקה ההופכית.
- יש העדפה לדרכים שאני הצעתי, בניגוד לפתרון הרבה מערכות משוואות.
- לא עקבתי ביחס לתרגיל, אבל בגדול מה שאמרת נשמע נכון.
- צריך לצטט את המשפט בלבד אלא ביקשו מכם להוכיח במפורש
- עשינו תרגיל כזה בכיתה. אתה מחשב מטריצה מייצגת שמעבירה מהבסיס הסטנדרטי לאנשהו ואז אתה מקבל נוסחא כזו:
![[T]_B^S[v]_S=[Tv]_B](/images/math/9/3/0/930685633edbb07f165ed090dd111cc2.png) . לכן
. לכן  הולך לצירוף הלינארי של איברי הבסיס B עם המקדמים מהכפל של המטריצה המייצגת בוקטור
הולך לצירוף הלינארי של איברי הבסיס B עם המקדמים מהכפל של המטריצה המייצגת בוקטור 
השאלות שנשארו
- בעצם מה שאני צריכה למצוא בתרגיל הזה. אוקיי תודה.
- וניתן להשתמש בזה בלי להוכיח, נכון?
- דרך הפתרון שלי דווקא פשוטה (רק 3 משוואות קלות), אבל באמת כדאי שאבין את עניין השימוש במטריצה המייצגת.
- טוב.
- מהו הניסוח המדוייק של המשפט הזה?
- הנוסחה היא ממש משפט, לא? אבל לא הבנתי מה כתבת פה: לכן
 הולך לצירוף הלינארי של איברי הבסיס B עם המקדמים מהכפל של המטריצה המייצגת בוקטור
הולך לצירוף הלינארי של איברי הבסיס B עם המקדמים מהכפל של המטריצה המייצגת בוקטור  . בבקשה תסביר ברור יותר, ממש חשוב לי להבין את זה (והתרגיל מהכיתה לא כתוב לי, העדפתי להקשיב).
. בבקשה תסביר ברור יותר, ממש חשוב לי להבין את זה (והתרגיל מהכיתה לא כתוב לי, העדפתי להקשיב).
- כן
- חשוב להבין כי יהיו שאלות ישירות על מטריצה מייצגת שלא תוכלי להתחמק מזה.
- תחפשי במחברת הרצאה הכי טוב
- הנוסחא היא משפט כן. את יודעת ש
![[T]_B^S[v]_S=[Tv]_B](/images/math/9/3/0/930685633edbb07f165ed090dd111cc2.png) . מה המשוואה הזו אומרת? מצד שמאל יש את המכפלה של המטריצה המייצגת בוקטור
. מה המשוואה הזו אומרת? מצד שמאל יש את המכפלה של המטריצה המייצגת בוקטור  . מצד ימין מקבלים את הקואורדינטות של Tv לפי הבסיס B. לכן צירוף לינארי של איברי הבסיס B עם המקדמים שהם המכפלה משמאל שווים בדיוק לTv (הרי זו ההגדרה של קואורדינטות).
. מצד ימין מקבלים את הקואורדינטות של Tv לפי הבסיס B. לכן צירוף לינארי של איברי הבסיס B עם המקדמים שהם המכפלה משמאל שווים בדיוק לTv (הרי זו ההגדרה של קואורדינטות).
מובן?
- אהה.. נראה לי שהבנתי! תודה רבה!! אנסה לפתור את התרגיל בשתי הדרכים.
2.15
מה הכוננה של (v(Ta בסעיף ב'? תודה
- ההגדרה בעמוד 56
מבחן תשסה מועד ב' שאלות אמריקאיות שאלה 10
למה הטענות הנכונות הן א' וד'? אני חושב ש ב' וג' לא נכונות וגם א' לא נכון. למה א' נכון? א' אומר שכל הפונקציות מR לR הן כל הפונקציות הזוגיות סכום ישר עם כל הפונקציות האיזוגיות. זה לא נכון, כי יש פונקציות שהן לא זוגיות ולא איזוגיות ולא הסכום שלהן, כמו f(x)=x+1 או f(x) =rootX. (שורש של X). ויש גם פונקציות שהן גם זוגיות וגם איזוגיות, כמו f(x)=0 לא? כי אני זוכר מהבגרות שפונקציות זוגיות הן סימטריות ביחס לציר הX (מתקיים) ופונקציות אי זוגיות סימטריות ביחס לציר ה-X "ואז" לY (כלומר לשקף את מה שמימין לציר הX ומשמאל לציר הX ואז זה אמור להיות סימטרי ביחס לציר הY). אני טועה? תודה
תשובה
- כל פונקציה היא סכום של זוגית ואי זוגית, ספציפית עשינו את זה בתרגיל.
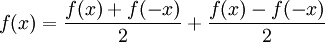
- אתה יודע למה ב' לא נכון? מעל הממשיים הוא כן נכון. הבעייה היא, למשל, מעל
 שם יש את המטריצה
שם יש את המטריצה  שהיא גם סימטרית וגם אנטי סימטרית ושונה מאפס.
שהיא גם סימטרית וגם אנטי סימטרית ושונה מאפס.
- שתי דברים: דבר ראשון, לא הבנתי מהדוגמה שלך למה כל פונקציה היא סכום של פו' זוגית ואי זוגית (ואני לא זוכר שעשינו את זה בתרגיל). דבר שני, אז מה אם הפונקציה f(x)=0, היא לא גם זוגית וגם אי זוגית? תודה
- אתה יכול לוודא בקלות ש
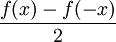 אי זוגית ו
אי זוגית ו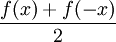 זוגית. 0 היא בוודאי גם אי זוגית וגם זוגית. לכן החיתוך הוא אפס, בדיוק כמו שאנחנו מצפים מסכום ישר.
זוגית. 0 היא בוודאי גם אי זוגית וגם זוגית. לכן החיתוך הוא אפס, בדיוק כמו שאנחנו מצפים מסכום ישר.
- אתה יכול לוודא בקלות ש
מבחן תשסה מועד ב' שאלות אמריקאיות שאלה 3
אוקי, עכשיו אני בטוח שיש פה טעות כלשהי. בתשובות כתוב שאפשרות 3 היא הבחירה הנכונה, כלומר 3 לא נכונה. זה לא הגיוני, כי לפי השאלה, יש לבחור רק תשובה אחת לא נכונה, כלומר אם 3 לא נכונה אז 1 2 ו4 נכונות- אבל תשובה 2 אומרת שאף אחת מהתשובות האחרות היא אינה נכונה, שאת המשפט הזה אפשר להבין ב2 דרכים: -כל התשובות האחרות לא נכונות, שזה לא יכול להיות כי עם 3 הוא לא נכון זה אומר ש 1 ו4 נכונות בסתירה לכך שכל התשובות האחרות לא נכונות. -כל התשובות האחרות נכונות, שזה לא הגיוני כי 3 הוא לא נכון. אז נכון שיש טעות כלשהי? אני חושב שהתשובה ההגיונית היחידה היא 2. תודה
תשובה
תשובה 3 היא משפט שקר.
אתה צודק שגם 2 הוא משפט שקר, זה פשוט בלבול של כותב השאלה.
rank
הrank של מטריצת האפס הוא אפס, נכון?
- כן
טעות במספר תעודת זהות
שלום,בציוני הבוחן והתרגילים ישנה אותה טעות במספר תעודת זהות שלי,בשניהם כתוב 205403933 אך המספר הנכון הוא 205413933. אשמח אם תוכלו לתקן זאת
- בסדר, תודה.
שאלה על rank
יהי T:V->V ה"ל וB,C בסיסים בV. מה זה rankT? מה זה rank([T]BC)? (כשBC אומר שיש B קטן בצד למעלה ימין של [T] וC קטן בצד ימין למטה)? תודה
תשובה
![rank([T]_C^B)](/images/math/f/0/6/f066ad93f39914e1457bd47190af2041.png) זה דרגה של המטריצה המייצגת ואנחנו יודעים את ההגדרה של דרגה של מטריצה. הדרגה של העתקה rankT זה המימד של התמונה (עמוד 56 בחוברת).
זה דרגה של המטריצה המייצגת ואנחנו יודעים את ההגדרה של דרגה של מטריצה. הדרגה של העתקה rankT זה המימד של התמונה (עמוד 56 בחוברת).
שאלה ממבחן
במבחן השני מועד א' שאלה אמריקאית 11, מה זה אומר שT היא מעל השדה Zp? זה אומר שהיא מZp לZp? מה זה אומר? איך זה יכול להיות שT היא מF לF כשF שדה, העתקה לינארית צריכה להיות ממרחב וקטורי למרחב וקטורי, לא? למה התשובה הנכונה היא 3? תודה.
תשובה
שדה הוא תמיד מ"ו מעל עצמו ממימד 1. לכן זו העתקה ממרחב וקטורי למרחב וקטורי. בשאלה מסתכלים על F כמ"ו מעל Z_p בכלל.
בכל אופן לא למדתם מאפיין ולכן השאלה לא ממש רלוונטית.
שאלה ממבחן
במבחן השני מועד א' שאלה אמריקאית 10, למה התשובה היא א,ב,ג, ולא כל הטענות נכונות?? הצלחתי למצוא מטריצות כך שכל הטענות יהיו נכונות-
א' וב' שתי מטריצות האפס
ג' A מטריצת האפס וB מטריצה גדולה ללא אפסים
ד' A מטריצה גדולה ללא אפסים וB מטריצת האפס..
תשובה
בד', AB=0 איך הדרגה שלו תהיה שווה לדרגה של A בדיוק?
שאלה ממבחן
במבחן השני מועד א' שאלה אמריקאית 9, למה הפתרון הוא 3? שמתי משתנים, דירגתי והגעתי למטריצת הזהות, כלומר כל האיקסים שווים לאפס? זה בטוח לא יכול להיות 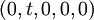 ! יש טעות? תודה
! יש טעות? תודה
תשובה
למעשה המשתנה השני *חייב* להיות חופשי. בגלל שאם היה לו איבר פותח המטריצה לא הייתה מדורגת כלל. לעומת זאת בעמודות האחרות ניתן להוסיף איבר פותח כך שכל שאר המשתנים יהיו אפס. כמובן שעוד פתרונות יתכנו, אבל לא פתרונות 1,2,4 בהם המשתנה השני אינו חופשי.
- "בגלל שאם היה לו איבר פותח המטריצה לא הייתה מדורגת כלל. לעומת זאת בעמודות האחרות ניתן להוסיף איבר פותח כך שכל שאר המשתנים יהיו אפס"- סליחה, ממש לא הבנתי למה התכוונת. מה זה איבר פותח, למה המשתנה השני חייב להיות חופשי, מה זה אומר שאם לא היה איבר פותח המטריצה לא הייתה מדורגת? גם אם הייתי יודע מה זה איבר פותח, למה דווקא המשתנה השני חייב להיות חופשי, למה לא השלישי הרביעי החמישי או הראשון? תודה
- כמו שאמרתי, חלק מהאחרים גם יכולים להיות חופשיים. אבל השני חייב להיות חופשי. איבר פותח או איבר ציר זה האיבר הראשון בשורה ששונה מאפס. איך יודעים אם משתנה הוא חופשי? אם אין איבר פותח בעמודה שלו. האופציה היחידה לשים איבר שונה מאפס בעמודה של המשתנה השני היא בשורה האחרונה. אבל השורה האחרונה חייבת להיות שורת אפסים על מנת שהמטריצה תהיה אכן מדורגת.
- מה?? המשתנה השני חייב להיות חופשי כי אין איבר פותח בעמודה שלו? אבל אפשר להחליף בין העמודה השניה לחמישית! והשורה האחרונה לא חייבת להיות שורת אפסים, דירגתי והגעתי לשורה ראשונה עם איבר פותח בעמודה הראשונה, שורה שנייה עם איבר פותח בעמודה השניה וככה לכל השורות!
- כמו שאמרתי, חלק מהאחרים גם יכולים להיות חופשיים. אבל השני חייב להיות חופשי. איבר פותח או איבר ציר זה האיבר הראשון בשורה ששונה מאפס. איך יודעים אם משתנה הוא חופשי? אם אין איבר פותח בעמודה שלו. האופציה היחידה לשים איבר שונה מאפס בעמודה של המשתנה השני היא בשורה האחרונה. אבל השורה האחרונה חייבת להיות שורת אפסים על מנת שהמטריצה תהיה אכן מדורגת.
- אי אפשר להחליף עמודות, ממתי מותר? נתונה מטריצה בצורה קנונית. אתה לא יכול לשים איזה מספרים שאתה רוצה, רק מספרים שישאירו את המטריצה מדורגת קנונית. נובע מכך, בהכרח, שהשורה האחרונה היא שורת אפסים. אחרת יש איבר פותח שאינו נמצא מימין ממש לאיבר הפותח שלפניו (והאיבר הפותח לפניו בעמודה האחרונה).
שיעור חזרה ביום ראשון
שיעור החזרה יהיה במתכונת של שאלות ותשובות, או שהמתרגל יפתור תרגילים?
פשוט אני עוברת על כל המחברת ועד עכשיו יש לי בערך 7 שאלות, כדאי לשאול אותן פה, או לחכות לשיעור? (קשה יותר לשאול ולהסביר פה..)
תשובה
שיעור החזרה יהיה עם חומר מוכן מראש.
פרט לכך, נשאר אתכם כמה שצריך אחרי כן לענות על שאלות (לא כל המתרגלים, אבל לפחות אני).
בנוסף, אפשר לרשום פה בוודאי.
- תודה על התשובה המהירה! מי אתה?
- ארז.
- אה יופי אתה המתרגל שלי.
- ארז.
עמוד 49 שאלה 11.8
עבור מטריצה A=1-0-0,0-1-0 (מסדר 2 על 3), אני טוענת ש-rankA=2. צריך להסביר משהו מעבר ל: "לפי הבסיס הסטנדרטי rankA=2"?
תודה.
תשובה
מה הכוונה לפי הבסיס הסטנדרטי? ניתן לומר "זו מטריצה מדורגת. דרגת המטריצה שווה למספר השורות השונות מאפס בצורה המודרגת שלה. יש פה 2 שורות שונות מאפס"
- טוב.. פשוט זה נורא ארוך לתרגיל שכולו 2 שורות ><. תודה.
- יש לי רעיון, אכתוב "דרגת מטריצה מדורגת שווה למספר השורות השונות מ-0 בצורתה המדורגת" ואסמן בכוכבית, ואז בכל פעם אכתוב "לפי * rankA=2". אחרת, זה נורא ארוך וסתמי, לחזור על אותו המשפט 9 פעמים!
שאלה ממבחן 2005 מועד א
במבחן השני מועד א' שאלה אמריקאית 2, z^3=x3 כשx שווה לצמוד של z. למה אף אחת מהתשובות לא נכונה? יצא לי שim(z)=0 גם כשהתעסקתי בZ כa+bi וגם כrcisO. זו טעות או שאני טועה? תודה
תשובה
מה לגבי 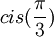 ?
?
2.11
בשאלה 2.11 בב' כתוב שיש העתקהה s:v -> v וs לא שווה לאפס. לא נאמר ש S העתקה לינארית, האם כשאני מוכיל שב' שקול לא' אני צריך להוכיח שS לינארית, או שהיא סתם העתקה? תודה
תשובה
הכוונה לS העתקה לינארית, אחרת מה קשור משפט ההגדרה?
שאלה ממבחן
אם נתון לי ש
- T(1+2x+xx)= (1,1,2)
- T(1+x+2xx)=(2,1,1)
- T(2+x+xx)=(1,2,1)
אז אני יכול להגיד שפשוט T(axx+bx+c)= (c,b,a) ואז זה ממש ממש פשוט להוכיח שT חח"ע ועל? ועוד שאלה קטנה, כתוב בתחילת השאלה שT העתקה לינארית, אז זה אומר שכדי להוכיח שT איזומורפיזם אני לא צריך להוכיח שהיא העתקה לינארית נכון? תודה.
תשובה
אי אפשר פשוט להגיד את זה, צריך להוכיח את זה.
אף פעם לא צריך להוכיח את הנתון. אם רשום "נתונה העתקה לינארית" אין צורך להוכיח את זה.
2.8
סלחו לי אם אני כותב את התשובה, אבל לא קיבלתי מענה האם ההוכחה שלי נכונה או לא- האם אני יכול להוכיח שv=imT1=imT2 כך? x שייך לimT1 וy שייך לimT2 וv שייך לV.
- x+y /T1() -> =T1(x)+ T1(y) /+T2(v) -> =T1x+T1y+T2v ->T2() -> =T1T2x+T1T2y+T2T2v =0+T2T2v =T2v
- v /T1() -> =T1v /+T2v -> = T1v+T2v =Iv=v /T2() -> =T2v
(עשיתי אותן פעולות והגעתי לכך ששני האגפים שווים). ואז רק להוכיח שחיתוך הimים זר, וזה בסדר? או שזה לא נכון? תודה!
- לא קיבלת מענה, כי בשביל זה יש בדיקת תרגילים. ביום ראשון יפורסמו פתרונות לתרגילים בכל מקרה.
- אני לא יקבל את התרגיל עד המבחן ואני רוצה לדעת אם הפתרון שלי גם בסדר...
- אז תשאל שוב יום ראשון.
- למחוק את השאלה?
- אז תשאל שוב יום ראשון.
- זה בסדר, תודה :)
6.14
סעיף א: האם צריך להשלים את הה"ל לפי הבסיס הסטנדרטי , ואז למצוא את T בצורה מפורשת? וכן בסע' ב' האם לשלוח את הוקטורים הנתונים ל-0, ולהמציא וקטור שלישי (בת"ל בשניים הנתונים) ו"לשלוח אותו" לסתם וקטור כלשהו, ואז למצוא את T... אבל אז סע' ב' וג' יכלים להיות זהים? נכון?
תשובה
בסעיף א' צריך למצוא את ההעתקה בצורה מפורשת. מה להשלים למה זה בחירה שלך, העיקר שיקיים את תנאיי הסעיף.
כנ"ל לגבי הסעיפים האחרים.
בוודאי שכל העתקה לינארית מסעיף ג' עונה על התנאים של סעיף ב'.
שאלה בקשר לתשובה
האם צריך להראות איך הגענו לההעתקה המסויימת או שפשוט להראות שהיא מקיימת את התנאים?
תשובה
צריך לפרט בתרגיל הזה, שכן הוא בוחן את ההבנה של משפט ההגדרה, ומציאת העתקה המפורשת מתוך ההגדרה
- התכוונתי האם צריך להסביר איך הגעתי להעתקה עצמה או להראות שזה מתקיים עבור בסיס כלשהו ואז להשתמש במשפט ההגדרה ולהגיע לכללית? (האם צריך להסביר למה בחרתי ככה את ההעתקה עבור האיברים של הבסיס ואיך הגעתי אליה??) ודבר נוסף האם מותר לי להגדיר את ההעתקה שלי כלינארית ואז להשתמש במשפט ההגדרה (כי אני נותן את הערכים שאליהם נשלח הבסיס) ולהגיע להעתקה הכללית? (מותר לי להגדיר אותה כלינארית בכלל בתרגיל הזה? לא שאני רואה דרך אחרת..)
1.28
האם זה נכון להוכיח ש imT1=kerT2, ומכאן נובע שהסכום ישר לפי 2.7 ב. כי T2 אידמפוטנטית?
תשובה
אם זה נכון זה בסדר, ואם זה לא נכון אז לא :)
כמה שאלות
- דורש הוכחה או טריוויאלי? קבוצה D פורשת מ"ו V. ב-D יש n איברים. האם צריך להסביר למה מכך נובע ש- dimV<=n? (אפשר להניח בשלילה ש-k=dimV>n ואז אם d שייך ל-D, נוסיף ל-D עוד k-n איברים מהצורה ad כאשר a בשדה. נקבל קבוצה חדשה E שפורשת את V וגם dimE=k לכן E בסיס ל-V, אבל E ת"ל כי
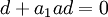 כאשר
כאשר 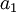 בשדה אבל
בשדה אבל 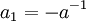 שונה מ-0. קיבלנו סתירה לכך שבסיס הוא בת"ל, מ.ש.ל) ההוכחה די ארוכה והיא לא מטרת התרגיל (11.2), אבל מצד שני, האורך שלה מראה על כך שהיא לא ממש טריוויאלית.. בקיצור - צריך או לא צריך?
שונה מ-0. קיבלנו סתירה לכך שבסיס הוא בת"ל, מ.ש.ל) ההוכחה די ארוכה והיא לא מטרת התרגיל (11.2), אבל מצד שני, האורך שלה מראה על כך שהיא לא ממש טריוויאלית.. בקיצור - צריך או לא צריך? - מה זה cspan? אם יש כזה דבר בכלל..?
- הציון שלי של תרגיל 3 לא מופיע, למה ומה לעשות בנושא? (הגשתי אותו!)
תודה מראש!!
תשובה
- לא צריך להוכיח את זה אלא מבקשים במפורש. מספיק לצטט את המשפט מההרצאה.
- אני מנחש שזה קיצור של Columne Spane כלומר מרחב העמודות. אני לא נתקלתי בזה, אני לא יודע אם ראיתם את זה בהרצאה או לא.
- לשלוח למתרגל שלך מייל בנושא.
תשובה לתשובה
תודה!
- איזה משפט בדיוק?
- אני ראיתי את זה בשאלה שמתחת לזו...
- אוקיי תודה.
- לא יודע, תפתח מחברת ותחפש. כנראה שיהיה מספיק לכתוב "לפי משפט, מספר האיברים בקבוצה פורשת גדול או שווה למימד"
- נראה לי שהמשפט שאומר שאם יש קבוצה שפורשת את V, וקבוצה בת"ל מוכלת ב-V אז מספר האיברים בפורשת גדול שווה ממספר האיברים בבת"ל.
המבחן
ביום שלישי יש מבחן בלינארית. כמה זמן המבחן? מתי הוא מתחיל? כמה שאלות? מה המבנה?
תשובה
מה שאמרו בהרצאה. אם לא אמרו, אפשר לשאול ביום ראשון בחזרה
מה אמרו בהרצאה? אני לא יכול להגיע ביום ראשון לחזרה, אתם משאירים אותי פה במתח.
11.10
האם אני יכול להגיד ש- dim(cspan(A)+cspan(B))=rank(A+B)?
תשובה
לא, זה לא נכון. קח (A=(-B
שאלה 6.14
אפשר הכוונה לגבי 6.14? תודה רבה!
- הרמז שרשום שם מכוון מצויין.. משפט ההגדרה, השלמה לבסיס. אם תוכל לכוון אותי לבעייה, אני אוכל לכוון אותך לפתרון.
- התכוונתי לגבי א'. תודה
- כן, לגבי א'. משפט ההגדרה במפורש. הרי התמונה של ההעתקה היא המרחב הנפרש על ידי ה-w_i מהמשפט.
- התכוונתי לגבי א'. תודה
2.8
מה זה אומר ש T1+T2 = Iv? אני יודע מה זה Iv, אני מתכוון ל-מה זה אומר הסכום שלהם? כאילו ש T1v1+T2v2=v1+v2 או ש T1v+T2v=v? או מה? זה ממש לא מובן. תודה
תשובה
תקרא את אותה שאלה עם התשובה למטה.
- סליחה לא שמתי לב! אני די בטוח שלא למדנו את זה אבל לא נורא. תודה
- אני בטוח לחלוטין (כמעט) שכן למדתם את זה ולכן זה דיי נורא כי זה חומר חשוב למבחן.
שאלה נוספת
וכשכתוב בב' T1T2, הכוונה היא הפעם לכפל של העתקות, כמו סכום? כי בדרך כלל זה הרכבה, אבל עכשיו נראה יותר מתאים שזה יהיה כפל. נכון? תודה
- ואז איך תגדיר? כפל של שני וקטורים? אין כזה דבר כפל של שני וקטורים. כפל בין העתקות לינארית הוא בלבד הרכבה. כפי שלמדנו
- אה, חשבתי שאם א. זה חיבור אז ב. זה יהיה כפל כזה D=TS -> D(v) = T(v)*S(v) אבל לא משנה.
עוד שאלה, לגבי דרך הפתרון
האם אני יכול להניח שקיימים x ששייך לimT1 וy ששייך לimT2 ואז להראות שאחרי כמה פעולות imT1+imT2 שווה לv ששייך לV אחרי אותן פעולות? אני ממש לא בטוח אם זה נכון, יש משהו לא נכון בהוכחה שלי? בנוסף, אני חושב שלא השתמשתי בעובדה שזה סכום ישר. זה בסדר? תודה!
- אין עובדה שזה סכום ישר, זה מה שצריך להוכיח. אם לא הוכחת את זה אז זה לא בסדר.
- ואתה לא צריך להראות שסכום של x וy הוא איבר בV זה טריוויאלי מסגירות. אתה צריך להוכיח שכל v בV הוא מהצורה v=x+y עבור x,y כלשהם בIm-ים המתאימים.
- אוקיי, אז אם אני לוקח v ששייך לV, ואחרי כמה פעולות מגיע ממנו לX+Y, זה בסדר?
- האם מותר לי גם (יהיה לי הרבה יותר קל אם כן) להניח שקיימים v,x,y כמו מקודם, ואז להראות אחרי כמה פעולות ש v=a וגם x+y=a
- (a ביטוי מסוים שלא אכתוב כדי לא לגלות את התשובה). זה בסדר? אפשר להגיד שאם זה ואם אין חיתוך בין הim-ים, אז ה-דרוש מתקיים?
- ועוד דבר, אני יכול להניח שT1 וT2 הפיכות? תודה!
- אי אפשר להניח דברים שלא בנתון. ושוב, אתה חייב להראות שכל v הוא מהצורה הנ"ל. איך תעשה את זה? זו החלטה שלך. הניסוח שלך קצת מצחיק- תקח x,y,v כללים ותוכיח שתמיד x+y=v? הרי וודאי לא יכול להיות שתצליח בזה.
2.7
אם אני מוכיח ב א' T היא העתקה הזהות זה בעצם מקיים את מה שהם מבקשים? או שצריך להראות שייש מקרים עבורם T שווה למינוס העתקת הזהות?(לפי מה שניסיתי לראות המקרה השני בכלל לא הגיוני וניתן לסתור אותו,אז אם צריך להראות שניתן שיתקיים שT שווה למינוס אז זו בעצם הפרחה, לא?)
תשובה
הלוגיקה חשובה במתמטיקה. אני אענה לשאלה, אבל חשוב לי להבהיר שאתם צריכים להיות מסוגלים להבין שאלה כזו לבד.
כאשר אומרים הוכח/הפרך, יש לומר אם המשפט הוא משפט שקר או משפט אמת.
במקרה הזה המשפט הוא: T המקיימת את תנאי השאלה היא בהכרח העתקת הזהות או מינוס העתקת הזהות.
אם כל T שמקיימת את תנאי השאלה היא העתקת הזהות או מינוס העתקת הזהות אזי המשפט נכון (מהגדרה).
לעומת זאת, אם קיימת T שמקיימת את תנאי השאלה ושונה מהעתקת הזהות וגם שונה ממינוס העתקת הזהות אזי המשפט הוא משפט שקר והפרכנו אותו.
- ככה חשבתי, פשוט זה נראה לי מוזר שבכלל הוסיפו את העניין עם המינוס אם הוא לא משנה בכלל, אז העדפתי לשאול. תודה
- יופי. תמיד טוב לשאול.
שאלה בקשר לשאלה והתשובה שנשאלו פה
רגע, אבל מה עם העתקת האפס, זה לא סותר את מה שאמרתם, העתקת האפס לא שווה להעתקת היחידה? לא?
יש לשים לב כי העתקה אידמפוטנטית מוגדרת  פרט ל-0 (בדר"כ) - בהסתמך על הערך "אידמפוטנט" [1]
פרט ל-0 (בדר"כ) - בהסתמך על הערך "אידמפוטנט" [1]
1.28
המטריצה המייצגת יצאה לי (x^2 2*x+3 3*x) זה הגיוני?ואז אני מדרג?הרי זה כמו וקטור שורה איך אני יכול לדרג? (לא ענית לי למטה..)תודה!
תשובה
כי מה שרשמת זה לא מטריצה. העמודות של המטריצה צריכות להיות וקטורי הקואורדינטות, בוודאי פולינום אינו יכול להיות עמודה של מטריצה.
ממליץ בחום רב לקרוא את המסמך על קואורדינטות ומטריצות מייצגות, יש שם דוגמאות והסברים לכל התהליך.
שאלה (שקשורה ל6.14)
האם העתקה T:V->W חייבת להיות מוגדרת לכל v בV? אני יודע שבהעתקות, לא חייב להיות לכל וקטור בW מקור, כי אני זוכר שהעתקה יכולה להיות על ולא על, אבל האם היא חייבת "לקחת" את כל הקטורים מV אל איברים בW אל לא? למשל, אם אני מגדיר העתקה מR4 לR4, האם אני יכול להגיד אותה כך? T(a,b,00) = T(0,0,a,b) אפילו שהוא לא מוגדר לכל V, או לא? תודה
תשובה
חייב להיות מוגדר לכל v, באופן כללי פונקציה צריכה להיות ח"ע ושלימה (כמו בבדידה)
1.14
אפשר בבקשה הכוונה איך אני מוכיח את א'? עם ב' הסתדרתי..
- אין סעיפים בשאלה 1.14
- התכוונתי להעתקת האפס!!
- מוכיחים את זה באמצעות הקריטריון המקוצר לבדיקת העתקה לינארית.
- אני יכול לעשות מעבר כזה: T(v+u) =0 כיוון ש לכל v ששיך לV מתקיים T(v)=0?
- מן הסתם... זו ההגדרה של העתקת האפס.
- תודה:)
שאלה
הדרגה של מטריצה עם 2 שורות ו2 עמודות שונות משורות אפסים, היא 2 או 4? לפי תשובה קודמת, נראה שכתבתם שהדרגה היא 2, אבל זה מביא לסתירה מסוימת, כי אם rank(A) =2 אם A מטריצה מגודל 2 על 2, אז זה אומר גם שהמימד של המרחב R2x2 הוא 2, לא? אבל חשבתי שהמימד של המרחב R2x2 הוא 4, כי בבסיס שלו 4 איברים {(0,0,0,1)(0010)(0100)(1000)} ? איפה אני טועה? תודה
תשובה
לפי תשובה קודמת, ראינו מטריצה כזו עם דרגה 1. אין קשר בין המימד של מרחב המטריצות, לפי המימד של מרחב השורות של המטריצה. הדרגה של מטריצה בגודל nxm היא קטנה שווה למינימום בין n,m. לעומת זאת מימד כל המטריצות הוא nm.
אם המטריצה בצורה מדורגת, הדרגה שלה היא מספר השורות השונה מאפס. בפרט, הדרגה לא יכולה להיות גדולה ממספר השורות.
- כמה שאלות: -מהי הגדרה של הדרגה של מטריצה? אם היא קטנה או שווה למינימום בין M,N, זה אומר שאי אפשר לחשב אותה במדויק?
- -אם יש מטריצה (מטריצות) שנראית כך: a, b, c, a+b+c
- (a וb בשורה הראשונה וה2 האחרים בשורה השניה), אז מימד המטריצות האלה הוא עדיין MN? אפילו שאחד האיברים במטריצה תלוי באחרים?
- -rankT כך שT הוא ממטריצות MxN למטריצות מאותו הגודל, הוא MN או המינימום? יש דבר כזה rankA וגם rankT כשA מטריצה וT העתקה? הם 2 סימונים ל2 דברים שונים? תודה רבה
תשובה
ההגדרה רשומה בעמוד זה, מספר פעמים. למשל #שאלה לתשובה ושתי שאלות מתחתיה.
אם תיקח תת מרחב של מרחב כל המטריצות שלא מכיל את כל המטריצות האפשריות, המימד שלו בהכרח יהיה קטן יותר. לגבי הדוגמא הספציפית צריך לוודא שזה אכן תת מרחב אחרת אין הגדרה למימד שלו.
rankT היא הדרגה של העתקה, אני לא יודע אם למדתם את זה או לא. אם כן, יש הגדרה במחברת שלכם. אם T העתקה לינארית ממרחב המטריצות למרחב המטריצות, היא העתקה בין מרחבים וקטוריים ממימד NM ולכן המטריצה שמייצגת אותה היא מגודל NMxNM, ולכן יכול להיות שהדרגה של המטריצה המייצגת הינה NM.
- תודה לגבי כל השאר, יש לי רק עוד דבר לא פתור: נניח שיש מטריצה (בוא נגיד, מסדר 2 על 2) כאשר אחד או יותר מהמקומות במטריצה הוא תלוי\ים במקומות האחרים (כמו בדוגמה שנתתי קודם, רק אם הדוגמה שנתתי לא טובה (כי היא לא תת מרחב וכדומה) אז דוגמה אחרת דומה -- המימד של המטריצות מהסוג הזה הוא עדיין MxN או לא? תודה.
דוגמא:
יהי מרחב המטריצות 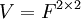 ויהי
ויהי 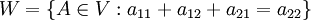 .
.
אזי קל לוודא שW תת מרחב של V ושהבסיס שלו הינו
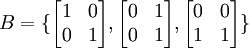
לכן המימד של W הינו 3.
המימד של V לעומת זאת הוא 4.
- איך מצאת את הבסיס של W?
1.28
מה הכוונה וקטור כללי מ R2[X ? נניח (1,1,1) הוא טוב?
תשובה
1. (1,1,1) הוא וקטור ספציפי - ההפך מכללי
2. במרחב הפולינומים ![\mathbb{R}_2[x]](/images/math/7/8/3/7833d694c27dce59ed3967e13de49400.png) הוקטורים הם פולינומים מדרגה קטנה שווה 2. לכן וקטור כללי במרחב זה הוא
הוקטורים הם פולינומים מדרגה קטנה שווה 2. לכן וקטור כללי במרחב זה הוא 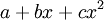
- את האמת שזה מה שחשבתי רק שלא הייתי בטוח..
- בכל מקרה, איך אני מחשב את ההעתקה ההפיכה?
- יש כמה דרכים. אחת מהן למדתם בהרצאה- בעזרת ההופכית של המטריצה המייצגת. הדרך השנייה היא לפי משפט ההגדרה - מספיק לבחור בסיס בתמונה ולראות מה המקור שלו וכך אפשר לחשב את המטריצה המייצגת של ההעתקה ההופכית.
- ראיתי הגדרה שאומרת: תהי f:A->B פונקציה. אם קיימת g:B->A כך ש f הרכבה g =למטריצה היחידה של A ו g הרכבה f= למטריצת היחידה של B נאמר
- שf הפיכה וg נקראת הפונקציה ההופכית של f.
- אי אפשר להשתמש בזה עבור הרכבה של העתקות לינאריות?
- אפשר לומר את זה על העתקות לינאריות, עם הסייג הבא: הרכבה של העתקות לינאריות אינה מטריצה אלא העתקה. כלומר ההרכבה של ההעתקות היא ההעתקת הזהות והמכפלה של המטריצות המייצגות היא מטריצת היחידה (שכן המטריצה המייצגת של העתקת הזהות מבסיס לעצמו היא תמיד מטריצת היחידה).
- המטריצה המייצגת יצאה לי (x^2 2*x+3 3*x) זה הגיוני?ואז אני מדרג?הרי זה כמו וקטור שורה איך אני יכול לדרג?
שאלה
צריך למבחן לדעת את העתקת האינטגרל, הנגזרת ועוד נושאים המוזכרים בחוברת של בועז צבאן ולא למדנו אותם??
תשובה
אין צורך לדעת דברים שלא נלמדו בהרצאה, בתרגיל או נתנו בשיעורי הבית.
כמובן שלא מזיק לפתור תרגילים נוספים, אבל אין צורך לזכור הגדרות אחרות.
שאלה למתרגלים (או למתרגל הספציפי שלי, אדם צ'פמן
למדנו נושא שלם (דטרמיננטות) שלא הזכרנו אותו אפילו בתרגול עם אדם צ'פמן. למה? המרצה אמר שהוא יכול להיות במבחן! תודה.
- מוזר, אנחנו מהקבוצה השנייה(עם אלי בגנו) לא למדנו דטרמיננטות בכלל גם לא בתרגול.
תשובה
אם הנושא יהיה במבחן, הוא יהיה בהתחשב בכך שלא היה תרגול. בהסמך על מה שלמדתם בהרצאה בלבד.
כמובן שלמי שלא למד את זה בהרצאה, זה לא יהיה במבחן.
תרגיל 11.8
מבקשים ממני בתרגיל לתת דוגמות למטריצות אשר מקיימות את התנאי המתבקש. האם אני צריך להסביר כיצד הגעתי לדרגה של המטריצות A ו-B שבחרתי או שפשוט לכתוב: "דרגתה של המטריצה A שנבחרה היא ... " ואותו כנ"ל עבור AB.
תודה מראש, גל.
- צריך רק להראות שהדרגה שלהן היא אכן כפי שאתה טוען.
תרגיל 11.2
האם x הוא בהכרח וקטור מסדר n*1 או שהוא יכול להיות מטריצה?
תשובה
הכוונה היא שb וx שניהם וקטורי עמודה (כלומר מגודל nx1 כפי שציינת)
- תודה!
- ועוד שאלה: כאשר נתון ש-
 הוא מרחב העמודות של
הוא מרחב העמודות של  , האם אני יכולה פשוט בלי להסביר כלום לכתוב ש:
, האם אני יכולה פשוט בלי להסביר כלום לכתוב ש: 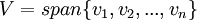 כאשר
כאשר  הם וקטורי העמודות של
הם וקטורי העמודות של  ?
?
- כן, זו ההגדרה.
בסיס
הוצאתי חוברת לינארית מהספרייה, ובספר כתוב שכדי לוודא שוקטורים מסויימים a1,a2,...ak בת"ל, צריך לשים את הוקטורים כעמודות של מטריצה הומוגנית, ואז לצטט את שני המשפטים הבאים: במטריצה המורכבת מהעמודות a1,a2,...,ak,b (כך שכל עמודה היא וקטור), הוקטור b הוא צירוף לינארי של a1,...,ak כך שהמקדם של ai לכל i הוא xi אם"ם (x1,...xk) הוא פתרון של המערכת שלמעלה. בנוסף ידוע כי מטריצת מקדמים מצומצמת (כלומר מקדמים של מערכת משוואות לינאריות הומוגניות) היא שקולה למטריצת היחידה אם"ם אין למערכת פתרון לא טריוויאלי. כלומר נוכיח שהמטריצה שהרכבנו מהעמודות a1,...,ak,b שקולה למטריצת היחידה עפ"י פעולות שורה אלמנטריות, ולפי זה פתרון המערכת x1,...,xk הוא טריוויאלי כלומר 0=(x1,...,xk) ולכן ל- 0=x1a1+x2a2+...+xkak יש רק פתרון טריוויאלי לכן לפי הגדרה הווקטורים a1,...,ak בת"ל.
השאלה שלי היא האם מספיק לנמק: ידוע שאם מטריצה שקולה למטריצת היחידה אז כל עמודותיה בת"ל? נימוק כזה קצר יכול לחסוך המון זמן וכאב ראש...
תשובה
למדנו את התיאור הראשון בתרגיל - וגם השתמשנו בזה בפתרון תרגיל 3 (בקובץ המצורף). כמו כן למדנו שניתן לדרג את המטריצה ולראות האם שורות התאפסו לנו. אלה שתי שיטות שונות ושתיהן נכונות.
חשוב לשים לב ששקילות למטריצה היחידה היא רלוונטית רק כאשר מדובר על מטריצה ריבועית. וקטורים יכולים להיות בת"ל גם אם תשים אותם בעמודות מטריצה והיא תהיה לא ריבועית.
חשוב לזכור שכאשר אנו שמים וקטורים בעמודות ומדרגים - אנו מסתכלים על מרחב הפתרונות. כאשר אנו שמים את הוקטורים בעמודות ומדרגים - אנו מסתכלים על מרחב השורות.
11.10
המטריצות A B הן שתיהן מגודל MXN?ובהוכחה אני אמורה להניח שהשורות הן בת"ל ושהדרגה שווה למס' השורות? אם שתי המטריצות הן מגודל MXN אז מה הדרגה?
תשובה
לעולם לא מניחים דברים שלא כתובים בנתון. הגדלים של המטריצות נתונים - וזה נכון.
השורות לא חייבות להיות בת"ל בכלל.
שאלה לתשובה
תודה על התשובה אבל לא כ"כ עזרת לי, ברור לי שאי אפשר להניח משהו שהוא לא נתון, השאלה שלי היתה האם כדי להוכיח את מה שרצו אני מניחה שהם בת"ל,הרי במקרה כללי אני חייבת להניח את זה..לא?ובנוסף לא ענית לי מהי הדרגה של מטריצה(כללית, כלומר שלא יודעם את אבריה) MXN?מימד מרחב השורות/העמודות?
תשובה
זה כמו לשאול: האם x זוגי? התשובה המתבקשת כמובן היא תלוי מהו x.
אי אפשר להניח ששורות המטריצה בת"ל, הרי בוודאי יש מטריצות ששורותיהן תלויות לינארית. למה שתניחי דבר שהוא לא בהכרח נכון?
אין כזה דבר דרגה של מטריצת כללית. שוב, הדבר דומה לשאלה מהם הגורמים הראשוניים של מספר כללי x.
כאשר מנסים לפתור תרגיל כזה צריך לגשת אליו בצורה טכנית. לתת שמות לשורות המטריצות A,B ואז לראות מהן שורות המטריצה A+B, ואז לראות איך אפשר לחשב את הדרגה כפונקציה של השורות האלה וככה לנסות לפתור את התרגיל.
באופן כללי יש משפט לפיו דרגת המטריצה = מימד מרחב העמודות = מימד מרחב השורות = מספר המשתנים התלויים במערכת ההומוגנית = מספר השורות השונות מאפס בצורה המדורגת של המטריצה
תרגיל 2.8
מה הכוונה ב(א) שכתוב 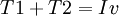 ? כלומר מה הכוונה בחיבור העתקות ליניאריות? תודה רבה... XD
? כלומר מה הכוונה בחיבור העתקות ליניאריות? תודה רבה... XD
תשובה
כמו שלמדנו בהרצאה ובתרגיל על המרחב הוקטורי של העתקות לינאריות -  :
:
יהיו 2 העתקות לינאריות T,S. נגדיר את ההעתקה הלינארית שהיא החיבור שלהן D=T+S, על ידי 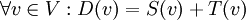
תשובה לתשובה
תודה רבה XD :P :) :D
מרחב עמודות ***עוד שאלה***
איך מחשבים את הדרגה של A, כלומר את מספר האיברים בבסיס של מרחב העמודות של A? איך מוצאים את הבסיס? מהי הדרגה של מטריצת האפס? למה? תודה.
תשובה
- הדרגה של המטריצה היא מספר השורות השונות מאפס בצורה המדורגת שלה.
- אפשר למצוא בסיס למרחב העמודות על ידי:
- שחלוף המטריצה A
- דירוג המטריצה המשוחלפת
- שורות הצורה המדורגת של המטריצה המשוחלפת השונות מאפס, מהוות בסיס למרחב העמודות (כאשר מסתכלים עליהן כעמודות כמובן)
- מטריצה האפס היא בצורה מדורגת, אין שורות שונות מאפס ולכן הדרגה היא אפס.
- תודה, אבל נראה לי (לפי הגיון) שהדרגה של מטריצה היא מספר השורות שגם לא תלויות אחת בשניה (בת"ל), לא? נגיד המטריצה
1 2
2 4
הדרגה שלה היא 1 או 2? תודה.
- הדרגה היא אחד. המושג הכללי שאתה מתאר (מספר השורות שלא תלויות אחת בשנייה) מוגדר במדויק - הוא נקרא מימד. מימד הוא מספר האיברים בבסיס. ואם תביא את המטריצה הזו לצורה מדורגת תראה בקלות שיש רק שורה אחת שונה מאפס בצורה המדורגת, והיא מהווה בסיס למרחב השורות.
תרגיל 11.2ב
מהי המטריצה A|b?
- המטריצה A שהוסיפו לה מימין את העמודה b.
סכום ישר
לא הבנתי עד הסוף את הנושא של הסכום הישר! אתה יכול לתת דוגמא?
גם היתה דוג' בהרצאה שלא ממש הבנתי,
V=R^3 u=sp{(1,1,1)}, w={(x1,x2,x3)|x1+x2+x3=0, x1,x2,x3 in R טענה- v=u+w
צ"ל :
1. U+W מוכל בV.
2.V תת מרחב של U+W
3.U חיתוך W שווה 0.
למה צריך להוכיח את 2??
תשובה
הביטוי  אומר את שני הדברים הבאים לפי הגדרה:
אומר את שני הדברים הבאים לפי הגדרה:
א. V=U+W
ב. 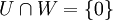
על מנת להוכיח את א, צריך להוכיח את 1+2 שלך (זו סה"כ הכלה דו כיוונית שמוכיחה שיוויון).
ב' הוא בדיוק 3 שלך.