הבדלים בין גרסאות בדף "בדידה לתיכוניסטים תש"ע - שאלות ותשובות"
(←שאלה 2א מועד ב 2009) |
(←שאלות) |
||
| (164 גרסאות ביניים של 24 משתמשים אינן מוצגות) | |||
| שורה 13: | שורה 13: | ||
'''[[בדידה לתיכוניסטים תש"ע - שאלות ותשובות - ארכיון 4| ארכיון 4]]''' - תרגיל 4 | '''[[בדידה לתיכוניסטים תש"ע - שאלות ותשובות - ארכיון 4| ארכיון 4]]''' - תרגיל 4 | ||
| + | '''[[בדידה לתיכוניסטים תש"ע - שאלות ותשובות - ארכיון 5| ארכיון 5]]''' - לקראת המבחן | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | =שאלות= | |
| + | ==המבחן=== | ||
| + | באיזה בניין וחדר יהיה המועד ב' בבדידה? | ||
| − | + | ==הפגישה== | |
| + | באיזה שעה הפגישה והיכן? | ||
| + | ==פקטור== | ||
| + | היה פקטור במבחן? | ||
| − | + | ===תשובה=== | |
| + | כן | ||
| − | + | ==חלוקת הציון== | |
| − | + | כיצד מחלקים את הציון? כמו בלינארית או שהבוחן ייחשב לכולם? ואם כן באיזה אופן? | |
| − | + | ||
תודה מראש, גל. | תודה מראש, גל. | ||
| + | ==ציונים== | ||
| + | מישהו יודע מתי יהיו ציונים? | ||
| + | ==שאלה חשובה ממבחן== | ||
| + | בכמה דרכים ניתן לחלק 40 עטים ממוספרים <math>(1,2,...,40)</math> בין 30 סטודנטים? | ||
| − | + | לא הבנתי את השאלה: | |
| − | + | *האם צריך לחלק את כל ה-40, כך שיהיו 10 סטודנטים שיקבלו 2 עטים? או לחלק רק 30 עטים? | |
| − | + | *האם מותר שחלק מהסטודנטים יקבלו 0 עטים? למשל - כל העטים לסטודנט אחד? | |
| − | + | ||
| − | + | אגב, תשובה סופית של השאלה תעזור לי מאוד, בשביל לבדוק את עצמי. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | == | + | ===תשובה (לא מתרגל)=== |
| − | + | כל האפשרויות הללו תופסות. אני הייתי פותר את השאלה כך: עבור כל עט יש שלושים אפשרויות, ולכן בסה"כ יש <math>30^{40}</math> אפשרויות. האם זה פתרון נכון? | |
| − | : | + | |
| − | + | :אני מניח שהכוונה ל40 עטים ספציפיים, כלומר לא יכול להיות שעט מספר 2 יהיה אצל שני תלמידים. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ::נו?תסתכל על זה כך - לעט 1 יש 30 אפשרויות (תלמיד 1 עד תלמיד 30) וגם לעט 2 יש 30 אפשרויות וגם ... וגם לעט 40 יש 30 אפשרויות. ולכן בסה"כ התשובה שציינתי מתקיימת | |
| − | + | ||
| − | + | :::צודק, טעות שלי. | |
| − | + | ||
| − | + | ||
| − | == | + | ==הוכחת יחס בפרט== |
| − | + | אם נתונה קבוצה B סופית ודי קטנה (כ-5 איברים) ואומרים יהי R יחס על B, הוכיחו ש-R יחס סדר חלקי (או שקילות, לא משנה). האם אני יכולה לכתוב בצורה מפורשת את R ופשוט לכתוב בצורה מפורשת למה היא טרנזטיבית, רפלקסיבית ואנטי סימטרית (או סימטרית), או שאני חייבת לעשות את זה באופן כללי ולא מפורש? | |
| + | ==2007 מועד ב'== | ||
| + | קישור: http://www.bis.org.il/download_Img.asp?file_name=278200810428508.pdf | ||
| − | + | בשאלה 1 צריך לרשום בצורת CNF ו-DNF שתי פונקציות שהן ביטוי לוגי. אין לי מושג על מה מדובר, אבל זה לא בחומר - נכון? | |
| − | + | שאלה 2 על דטרמיננטות - אני אמורה לדעת לפתור אותה ושאלה דומה יכולה להופיע במבחן מועד ב'? (אני עם אפי, למדנו דטרמיננטות שיעור אחד) | |
| − | == | + | בשאלה 4-ג',ד' ובשאלה 5 צריך להסביר משהו או רק לתת תשובה סופית? |
| − | + | ==מבחן 2007 מועד א'== | |
| + | קישור: http://www.bis.org.il/download_Img.asp?file_name=208200823203518.pdf | ||
| + | בחלק II שאלה 3 (שצריך להוכיח באינדוקציה), הבדיקה עבור n=1 יצאה לא נכונה! יש טעות בתרגיל או שאני טועה? | ||
| − | + | בבקשה תענו! | |
| − | + | ||
| − | + | דרך אגב, כל חלק III הוא לא בחומר, נכון? | |
| − | : | + | אה ועוד משהו: יש למישהו פתרונות של המבחן הזה? או לפחות פתרונות סופיים? אם מישהו פתר אותו, אז שיכתוב פה ונשווה :). |
| − | + | במיוחד חשובה לי השאלה בקומבינטוריקה: 1-ב', יצא לי 208. | |
| − | + | ||
| − | + | ==בקשה לפקטור== | |
| − | + | המבחן היה ברמה קשה מאוד אז נשמח לקבל פקטור. תודה! | |
| − | == | + | אני בטוח שבגלל שביקשת יהיה פקטור :) (לא שאני מתנגד ) |
| − | + | ::מצטרפת! | |
| − | + | ::מצתרף, וזה בלי קשר לבעיות הרבות שהיו, הפסקת חשמל, בעיות בתופס, ועוד.. או לפחות שיקימו מועד מיוחד כדי שהמועד ב' לא תיהיה ההזדמנות האחרונה, זה די מלחיץ, וגם באמת שהתנאים והרמה לא היו בסדר, בהצלחה לכל מי שהולך למועד ב' | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | == | + | ==שאלות על הפתרון== |
| − | + | בשאלה של התמורות, קבעתם את A להיות הקבוצה שבה איבר זוגי מסויים מופיע במקומו, ואז חישבתם את הסכום של כל הקבוצות האלו. אבל זה בעצם החיתוך של המשלימים, אז צריך לעשות את סך כל האפשרויות פחות הסכום שיצא, לא? | |
| + | ולגבי השאלה עם השוויון בין הסיגמות, אתם יכולים לכתוב את הפיתרון? (הוא לא מופיע). תודה! | ||
| − | + | ==פתרון המבחן== | |
| + | שלום. אתם יכולים בבקשה לפרסם את הפתרון של המבחן? תודה! | ||
| + | ==הצלחה במועד ב'== | ||
| + | שלום. אני נבחנתי במועד א' ונראה לי שנכשלתי ככה שגם בסופי יהיה לי ציון נכשל. אבל זה בכלל לא אומר שבמהלך כל הקורס ישבתי עם פה פעור ולא הבנתי מילה. עכשיו אני צריכה לגשת למועד ב', ובו אני רוצה להצליח. לא להצליח 80, אלא להצליח 100 לפחות. אני מוכנה לחרוש בשביל זה כמה שצריך, ואפילו יותר. אבל אני רוצה שהחרישה תהיה יעילה כמה שאפשר. אז מתרגלים, בתור מי שהצליחו באיזה קורס או שניים, בבקשה תספרו מנסיונכם, מהי הדרך הכי אפקטיבית ללמוד למבחן? מה ייתן לי את מירב הסיכויים לקבל 100? | ||
| − | |||
תודה מראש! | תודה מראש! | ||
| − | |||
| − | |||
| − | : | + | אני עדיין מחכה לתשובה, בבקשה... |
| − | + | :אני לא בטוח שהם עוד עוכבים אחרי הדף הזה, אבל אולי אם תשאל את השאלה בדף השיחה של אחד המתרגלים הם יענו לך (למשל [[שיחת משתמש:ארז שיינר]] ו[[שיחת משתמש:Adam Chapman]]. את רשימת כל מפעילי המערכת (רובם מתרגלים) תמצא [http://www.math-wiki.com/index.php?title=%D7%9E%D7%99%D7%95%D7%97%D7%93%3A%D7%A8%D7%A9%D7%99%D7%9E%D7%AA_%D7%9E%D7%A9%D7%AA%D7%9E%D7%A9%D7%99%D7%9D&username=&group=sysop&limit=50 כאן]). [[משתמש:אור שחף|אור שחף]], [[שיחת משתמש:אור שחף|שיחה]], 00:36, 10 בספטמבר 2010 (IDT) | |
| − | + | ::תודה לך :) | |
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | *קודם כל יש לוודא שיש לך את כל החומר מההרצאות ושאת מבינה כל דבר ודבר שנעשה בהרצאה (אחר כך כנ"ל לגבי התרגילים) | |
| + | *יש לעבור על מבחן מועד א' ולוודא שאת מבינה בדיוק איפה טעית, ואיך היית מקבלת 100 אם היית נגשת אליו. | ||
| + | *יש לפתור את כל תרגילי השנה ומבחנים משנים קודמות, דבר ראשון מבלי להסתכל בפתרונות, ולאחר מכן לוודא שפתרת נכון | ||
| + | *תנסי לקבוע שעת קבלה עם המתרגל שלך או מתרגל אחר בקורס שלך (עדיף באמצעות המייל, לא כולם עוקבים אחרי הדף הזה בשלב זה, כמו שאור ציין). | ||
| + | *אני אציין שמה שאמרתי הוא כללי מכיוון שאיני מתרגל בדידה ולכן איני יכול לכוון יותר למקצוע הזה. הכוונה נוספת תוכלי לקבל ממתרגלי בדידה. | ||
| − | + | בהצלחה, | |
| − | + | [[משתמש:ארז שיינר|ארז שיינר]] 00:52, 10 בספטמבר 2010 (IDT) | |
| − | + | ||
| − | + | ||
| − | + | ::תודה רבה!! | |
| − | + | ::מבין הדברים שכתבת, משנה מה אעשה קודם ומה אחר כך? ובשביל מה שעת קבלה? | |
| − | + | ||
| − | + | ||
| − | + | :::שעת קבלה לשאול שאלות (אם יש) וגם להתייעץ לגבי הלימודים ספציפית לקורס. לגבי הסדר, אני חושב שנוח לעבוד לפי נושאים הרצאה-תרגול-תרגיל בית (כלומר להבין את ההרצאה בנושא ואז את התרגול בנושא ואז תרגיל בית בנושא ואז לעבור לנושא הבא). אחרי שיש שליטה בחומר עוברים למבחנים ודברים דומים. | |
| − | + | ||
| − | == | + | ==עוד 2 שאלות קצרות ואחרונות בהחלט!== |
| − | + | יש לי עוד 2 שאלות קצרות שאפשר לענות עליהם עם תשובה סופית בלבד. | |
| + | :האם <math>P(AxB)=P(A)xP(B)</math>? | ||
| + | :נניח A=}1,2,3,{. מספר היחסים על A הוא 2 בחזקת 9 (לפי תשובה לשאלה קודמת), נכון? ומספר יחסים השקילות על A, איך מחשבים את זה? מחשבים אז זה בצורה אחרת, על ידי מספר מחלקות השקילות האפשריות נכון? המחלקות האפשריות הן 1,2,3; 12,3; 1,23; 2,13; 123; כלומר 5? או שיש לי טעות? תודה! | ||
===תשובה=== | ===תשובה=== | ||
| − | + | התשובה היא לא. <math>P(A \times B) = P(A) \times P(B)</math> זה שקר ברוב המקרים. אם <math>A=\{1,2\}</math> ו<math>B=\{3,4\}</math> אז <math>\{(1,3),(2,4)\} \in P(A \times B) \setminus P(A) \times P(B)</math>. הכי טוב להבין זאת דרך עוצמות. <math>|P(A \times | |
| − | + | B)|=2^{|A| \cdot |B|}, |P(A) \times P(B)|=2^{|A|+|B|}</math>. | |
| − | === | + | {{התנגשות}}לא. נניח בשלילה שזה נכון, אזי: |
| − | + | {| | |
| − | + | {{equation|l=<math>|\mathcal P(A\times B)|</math>|r=<math>2^{|A|\cdot|B|}</math>}} | |
| − | + | {{equation|o=<math>\not=</math>|r=<math>2^{|A|+|B|}</math>|c=קיימות <math>A</math> ו-<math>B</math> כך ש:}} | |
| − | + | {{equation|r=<math>2^{|A|}\cdot2^{|B|}</math>}} | |
| + | {{equation|r=<math>|\mathcal P(A)\times\mathcal P(B)|</math>}} | ||
| + | |} | ||
| − | + | בסתירה לכך שאם שתי קבוצות שוות אז עוצמתן שווה. [[משתמש:אור שחף|אור שחף]], [[שיחת משתמש:אור שחף|שיחה]], 14:38, 5 בספטמבר 2010 (IDT) | |
| − | + | :תודה! ובקשר לשאלה השנייה, עם מספר היחסים על A, צדקתי או שיש לי טעות? תודה | |
| − | + | ::לא משנה כבר, בהצלחה! | |
| − | + | ==2 שאלות, אם מתרגל עדיין נמצא פה..== | |
| + | -אם יש נוסחת נסיגה לא הומוגנית, שהאיבר החופשי שלה, במקום להיות מחובר מהצורה <math>a^n*q(n)</math> הוא פשוט מספר ללא n, לדוגמה 4, (כלומר: נוסחת נסיגה לדוגמה תהיה an=an-1+an-2+4) מה מציבים בנוסחת הנסיגה? פשוט k ללא n? או 4 בחזקת n כפול k? כי אם מציבים ביטוי ללא n, יש בעיה שהיא- מה להציב בan-1 וכו'. | ||
| + | -אם אפשר עזרה נוספת בנוגע[http://math-wiki.com/index.php/%D7%91%D7%93%D7%99%D7%93%D7%94_%D7%9C%D7%AA%D7%99%D7%9B%D7%95%D7%A0%D7%99%D7%A1%D7%98%D7%99%D7%9D_%D7%AA%D7%A9%22%D7%A2_-_%D7%A9%D7%90%D7%9C%D7%95%D7%AA_%D7%95%D7%AA%D7%A9%D7%95%D7%91%D7%95%D7%AA#.D7.91.D7.A2.D7.99.D7.95.D7.AA_.D7.A2.D7.A0.D7.A7.D7.99.D7.95.D7.AA_.D7.A2.D7.9D_.D7.94.D7.A8.D7.9B.D7.91.D7.AA_.D7.A4.D7.95.D7.A0.D7.A7.D7.A6.D7.99.D7.95.D7.AA..._-.D7.A2.D7.96.D7.A8.D7.94_.D7.91.D7.91.D7.A7.D7.A9.D7.94..- לשאלה הנל], תודה | ||
| − | === | + | ===תשובה=== |
| − | + | אם משוואת ההפרשים היא משהו בסגנון <math>f(n+k)=a_1 f(n+k-1)+\dots+a_k f(n)+c</math> כאשר c הוא קבוע (דהיינו מספר שלא תלוי בn) אז מחפשים פיתרון פרטי של משוואת ההפרשים שיהיה פונקציה קבועה, למשל <math>h(n)=b</math> ואז פותרים את המשוואה<math>b=a_1 b+\dots+a_k b+c</math> ומקבלים פיתרון <math>b=\frac{c}{1-(a_1+\dots+a_k)}</math> וממשיכים באלגוריתם לפיתרון נוסחת הנסיגה כרגיל. [[משתמש:Adam Chapman|Adam Chapman]] 12:55, 5 בספטמבר 2010 (IDT) | |
| − | : | + | :תודה! |
| − | == | + | ===עוד אפשרות=== |
| − | + | אם לא בא לך לזכור את כל המקרים אפשר להפוך את 4 ל- <math>(1^n)*4</math> | |
| − | + | ==שאלה לסיום== | |
| + | למדנו את הכלל-a כפול b= למקסימום של הערכים. | ||
| + | האם אפשר להסיק: | ||
| + | תהי k עוצמה. מכפלת k בעצמה שווה לk? | ||
| + | |||
| + | ===תשובה=== | ||
| + | ראשית להבהיר, למדנו את המשפט הזה לגבי עוצמות אינסופיות, עבור סופיות כמובן שזה לא עובד. | ||
| + | ושנית המכפלה תהיה שווה ל-k רק אם העוצמה קטנה או שווה ל-k | ||
| − | + | ==שיבוצי הכיתות== | |
| − | + | בניין 605 | |
| − | + | ||
| − | + | ||
| − | + | הקבוצה של אפי: <br> | |
| − | + | חדר 101: מסטודנט אבני תומר עד מלמד שירן <br> | |
| − | : | + | חדר 102: מסטודנט מרזוק חופית עד שרקנסקי אלה <br> |
| − | + | ||
| − | + | הקבוצה של שי: <br> | |
| − | + | חדר 103: מסטודנט אבוטבול עומר עד כרמל רום <br> | |
| − | : | + | חדר 104: מסטודנט לביא גל עד שרעבי רועי |
| − | == | + | ==חוקי עוצמות== |
| − | + | אחד החוקים שכתוב לי במחברת הוא שעבור עוצמות a,b,d מתקיים: אם <math>a<b</math> אז <math>a^d<b^d</math>. השאלה היא מהן העוצמות a,b,d, האם זה גם עבור עוצמות סופיות? | |
| − | : | + | השאלה היא בהמשך לדוגמה נגדית שמישהו נתן: <math>2<3</math> אבל 2 בחזקת א0 שווה 3 בחזקת א0. |
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | כנראה זה קטן שווה, גם אם d=0 יש שוויון | |
| + | :כן, כנראה. תודה. בכל מקרה, תשובה חד משמעית ממתרגל תעזור. אולי אפשר ממש להגיד מתי קורה השוויון, ואז להגביל a,b,d כך שהוא לא יקרה אף פעם? | ||
| + | ::אני לא מתרגל, אבל לפי דעתי אם זה גדול ממש זה לא תורם יותר מדי, לעומת זאת אם זה גדול שווה זה מראה על קיום פונ' חחע מצד אחד ופונ' על מצד שני. | ||
| − | + | ===תשובת מתרגל=== | |
| + | אני כן מתרגל, והאמת היא שאם קבוצות מקיימות <math>|A| \leq |B|</math> אם ורק אם קיימת פונקצייה על מB ל A שזה קורה אם ורק אם יש פונקצייה חח"ע מA לB. המשמעות של <math>|A| < |B|</math> היא שקיימת פונקצייה על מB לA אך לא קיימת פונקצייה על מA לB, שזה קורה אם ורק אם קיימת פונקצייה חח"ע מA לB אך לא קיימת פונקצייה חח"ע מB לA. | ||
| + | בהצלחה במבחן היום! [[משתמש:Adam Chapman|Adam Chapman]] 12:28, 5 בספטמבר 2010 (IDT) | ||
| − | |||
| − | + | :טעות שלי, החוק באמת כתוב עם שווה גם במחברת. | |
| − | + | ==מתי המבחן?== | |
| + | בשלוש וחצי או ארבע? האם התשובה היא ב100 אחוז? תודה! | ||
| + | : בארבע, זה הרי מה שנכתב כאן ובמערכת המידע האישי... | ||
| + | ואיפה? | ||
| + | :שוב, מערכת מידע אישי ולפי מספר קורס 88195 (ולאחר מכן 08 עבור אפי 11 עבור שי) תוכל לראות באיזה חדר אתה משובץ | ||
| − | 4 | + | ==שאלה 1, סעיף 4 בדף רקורסיה== |
| + | שלום רב, | ||
| − | + | אם מבקשים ממני את מספר תתי הקבוצות של <math>\{1,...,n\}</math> שבהן יש מספרים עוקבים (ביחס רקורסיה), האם מותר לי לפתור כך: | |
| − | + | " | |
| + | עפ"י הסעיף הקודם (סעיף 3) קיבלנו שמספר האפשרויות לתתי הקבוצות של הקבוצה הנתונה בהן אין מספרים עוקבים בכלל הוא <math>f(n)=f(n-1)+f(n-2)</math>. מכיוון שלכל תת קבוצה יש שתי אפשרויות (שתכיל עוקבים או שלא תכיל עוקביים) ויש בסה"כ <math>2^n</math> תתי קבוצות אז נגדיר <math>g(n)</math> להיות מספר הקבוצות בהן יש מספרים עוקבים ולכן <math>g(n)=2^n-f(n)=2^n-f(n-1)-f(n-2)</math>?" | ||
| − | + | אם לא, איך אני יכול לפתור? תודה, גל. | |
| + | ==תרגיל 2== | ||
| + | איפה התשובות של שאלות 8,9? (http://www.math-wiki.com/images/1/1d/10BdidaTargil2Sol.pdf) | ||
| − | + | ==אפשר עזרה בשאלה 3 2008 מועד ב' סעיף ב'?== | |
| + | אני כבר ממש מיואש, כל פונקציה שאני בונה יוצאת לא חחע ולא על! זאת שאלה ממש קשה, אבל גם ממש חשובה למבחן, אז אפשר, בבקשה, פתרון או הכוונה? תודה! | ||
| − | + | ===תשובה=== | |
| − | + | בשאלה הזו לא מצפים ממך לבנות פונקציה כי אם להשתמש בחוקים אלמנטריים שאתה יודע בחשבון עוצמות. | |
| − | + | ההוכחה שמצופה מכם היא כזו: | |
| − | + | מצד אחד <math>2^\lambda>\lambda</math> ולכן <math>(2^\lambda)^\lambda=2^\lambda</math>. | |
| − | : | + | מאידך, <math>2 \leq k \leq 2^\lambda</math> ולכן <math>2^\lambda \leq k^\lambda \leq (2^\lambda)^\lambda=2^\lambda</math> ולכן <math>k^\lambda=2^\lambda</math>.[[משתמש:Adam Chapman|Adam Chapman]] 19:33, 4 בספטמבר 2010 (IDT) |
| + | :אני פשוט לא מאמין, סתם ישבתי לי ובניתי פונקציות.. | ||
| + | :בכל מקרה, לא הבנתי אף אחד מהשלבים שעשית! קראתי שוב לאט, ובטוח גם אם הפתרון שלך נכון אז חסר בו פירוט הכרחי באיזשהו מקום- איך אתה יודע שK בחזקת גימל שווה ל2 בחזקת גימל? | ||
| + | ::כי <math>2^\lambda \leq k^\lambda \leq 2^\lambda</math> | ||
| − | |||
| − | + | ::לימדו אתכם בהרצאה שאם k אינסופית אזי לכל <math>\lambda<k</math> מתקיים <math>k^\lambda=k</math>. גם לימדו אתכם בהרצאה שאם עוצמה k קטנה מקיימת <math>\gamma \leq k \leq \gamma</math> אז <math>k=\gamma</math>. אלו הם שני החוקים שהשתמשתי בהם בהוכחה הנ"ל. [[משתמש:Adam Chapman|Adam Chapman]] 19:48, 4 בספטמבר 2010 (IDT) | |
| + | :::לא!!! התכוונתי לאיך אתה יודע את כל אחד מ2 השלבים האלה! ברור לי שאם אתה יודע שאחד גדול מהשני והשני גדול מהראשון אז על פי קנטור ברנשטיין יש שוויון!!את התוצאה <math>2^\lambda \leq k^\lambda \leq 2^\lambda</math> פשוט המצאת. כמו כן פשוט כתבת שאם<math>2^\lambda>\lambda</math> אז <math>(2^\lambda)^\lambda=2^\lambda</math> וש <math>2^\lambda>\lambda</math> אז <math>(2^\lambda)^\lambda=2^\lambda</math>בלי להסביר! מאיפה הבנת את הדברים האלה?? אתה יכול להסביר בבקשה למה K בחזקת גימל גדול מ2 בחזקת גימל ולמה להפך?? תודה | ||
| − | |||
| − | + | :::לימדו בהרצאה שאם k אינסופית אזי לכל <math>\lambda<k</math> מתקיים <math>k^\lambda=k</math>. במשפט הזה תחליף את k ב-<math>2^\lambda</math> (אינסופי כי <math>\lambda</math> אינסופית נתון). ידוע ש- <math>\lambda<2^\lambda</math> לפי קנטור. לכן לפי המשפט הזה, <math>(2^\lambda)^\lambda=2^\lambda</math>. | |
| − | + | :::חוץ מזה, ידוע שכאשר a,b,c עוצמות: אם a<b, אז <math>a^c<b^c</math> ולכן אם נתון <math>2 \leq k \leq 2^\lambda</math> אז <math>2^\lambda \leq k^\lambda \leq (2^\lambda)^\lambda=2^\lambda</math> (העלינו הכל בחזקת <math>\lambda</math> והשיוויון ממה שהוכחנו קודם). זהו עכשיו לפי קנטור ברנשטיין מ.ש.ל. אגב אני לא מתרגלת אבל מקווה שעזרתי. | |
| + | ::::תודה על העזרה, אדם, אני ממש לא רוצה להעליב, אבל אי אפשר להבין כשישר כותבים תוצאה. אבל נראה לי שיש פה טעות, כי למשל למשפט אם a<b, אז <math>a^c<b^c</math> אני יכול לתת דוגמה נגדית. ודבר שני, אני ממש לא זוכר שלמדנו בהרצאה את מה שאת ואדם אמרתם שלמדנו. תודה | ||
| − | + | :::::איזו דוגמה נגדית? (שים לב ש-c זו עוצמה, לא משלים. הסימונים שהשתמשתי בהם הם לא משהו..) אם אתה עם אפי, אז החוק הזה כתוב לך בעמוד האחרון שלפני קומבינטוריקה (מצחיק, הרגע שמתי לב שכל התרגיל הזה הוא חוק מספר 8 שכתוב שם במדוייק). | |
| − | :אם | + | :::::את מה שאדם כתב אין לי במחברת. בכלל, בקושי יש חוקים שלמדנו על עוצמות כלשהן (כשלא ידוע מהי העוצמה). אם הייתה רשימה של כל החוקים האלו זה היה כ-ל-כ-ך עוזר! |
| − | :: | + | ::::::למשל, 2 בחזקת א0 שווה ל3 בחזקת א0, לא? |
| + | :::::::וואלה, נראה לי שאתה צודק... אז אולי החוק הזה הוא אם a,b,c עוצמות אינסופיות? לא יודעת. יש איזה מתרגל שיכול לעזור פה? | ||
| − | + | ===תשובת מתרגל (אע"פ שהתשובת המתרגל כבר רשומה למעלה)=== | |
| − | : | + | אני מתרגל, ואין לי מושג מי היה המתרגל או המרצה שלכם, חברה, אך נדמה לי שלא רשמתם במחברתכם את כל מה שנאמר בהרצאות או בתרגולים. אני נתתי את רשימת החוקים של חשבון עוצמות גם בתרגול שלי וגם בתרגול העזר של הקורס. שני החוקים שרשמתי למעלה (בפרט הראשון) הם נכונים ונוסחם הוא בדיוק מה שניסחתי לכם למעלה. בהצלחה במבחן! [[משתמש:Adam Chapman|Adam Chapman]] 12:31, 5 בספטמבר 2010 (IDT) |
| − | == | + | ==בעיות ענקיות עם הרכבת פונקציות... -עזרה בבקשה..-== |
| − | + | זהו המשך לשאלה ששאלתי קודם, [http://math-wiki.com/index.php/%D7%91%D7%93%D7%99%D7%93%D7%94_%D7%9C%D7%AA%D7%99%D7%9B%D7%95%D7%A0%D7%99%D7%A1%D7%98%D7%99%D7%9D_%D7%AA%D7%A9%22%D7%A2_-_%D7%A9%D7%90%D7%9C%D7%95%D7%AA_%D7%95%D7%AA%D7%A9%D7%95%D7%91%D7%95%D7%AA#3_.D7.A9.D7.90.D7.9C.D7.95.D7.AA_.D7.A2.D7.9C_.D7.94.D7.A8.D7.9B.D7.91.D7.AA_.D7.A4.D7.95.D7.A0.D7.A7.D7.A6.D7.99.D7.95.D7.AA השאלה]. אני ממש, ממש תקוע, בסעיף א' כיוון שמאלה, ובסעיף ב' שני הכיוונים (אדם, כנראה שלא הבנתי את הפתרון שלך). למשל ב-ב', אם f חחע, אז לפי מה שהבנתי (וגם בדקתי את זה!) היא הפיכה '''משמאל''' ולא מימין. לכן קיימת פו' כך ש hf=id. אבל זה ממש בעייתי ולא עוזר לפתור את הבעיה, כי צריך להוכיח שלכל תמונה של פי, כלומר לכל gf, קיים מקור g, אבל איך אפשר להוכיח את זה, הרי גם אם נרכיב את ההופכי של f משמאל, יצא hgf, שזה לא נותן כלום! מה עושים? (אם אפשר תשובה מפורטת גם לזה וגם לסעיפים\כיוונים האחרים) תודה רבה! | |
| − | + | ||
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | אכן הייתה לי טעות בהקלדה אך כדאי שתקרא את התשובה שרשמתי למטה שוב. | |
| − | + | ||
| − | + | עכשיו אולי אוסיף משהו שיסייע להבנה: | |
| − | + | ||
| − | + | ||
| − | : | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | אם אתה רוצה להוכיח שפי היא על אתה צריך לקחת איבר בטווח ולהראות שיש לו מקור ,כלומר איזשהו g כך שgf שווה לאיבר בטווח שלקחת. אף אחד לא אומר לך שהאיבר בטווח הוא מן הצורה gf. זה מה שאתה צריך להוכיח! | |
| − | + | ||
| − | + | ||
| + | אתה צריל לקחת איבר כללי בטווח, אותו <math>\psi</math> ומראה שקיימת g כך ש<math>\psi=g \circ f</math>. | ||
| + | זה מה שעשיתי בוהכחה למטה. אני ממליץ לך לקרוא אותה שוב.[[מיוחד:תרומות/79.180.9.140|79.180.9.140]] 19:16, 4 בספטמבר 2010 (IDT) | ||
| + | : | ||
| + | :לא הבנתי את המשפט:"לכל פונקציה <math>\psi \in C^A</math> יש מקור <math>g=\psi \circ h \in C^B</math> לפי פונקציה <math>\Phi</math>, כי <math>\Phi(g)=g \circ f=\psi \circ h \circ f=\psi</math>", באמת שלא הבנתי למה G שווה לפסי הרכבה H ומה זה אומר "לפי פונקציה פי". אפשר הסבר קצת מפורט יותר? תודה! | ||
| − | == | + | ::אתה צריך להראות שקיימת g כך ש<math>\psi=g \circ f</math>. לא נתונה לך g שאתה צריך להוכיח שהיא <math>g=\psi \circ h \in C^B</math>. אתה יכול לבחור איזו g שאתה רוצה. אתה רק צריך להסביר למה אותה g שבחרת היא מקור לפסי. אני בחרתי את g להיות הפונקציה <math>\psi \circ h</math> והראיתי שהיא אכן מקור לפסי. מכיוון שפסי הוא שרירותי זה אומר שהראיתי שלכל פסי שרירותי קיים מקור, ולכן פי היא על. כדי להראות שקיים מקור לאיבר אתה צריך לציין את המקור הפוטנציאלי ולהראות שהוא אכן מקור. המקור הוא לא מ שנתון לך. [[משתמש:Adam Chapman|Adam Chapman]] 19:42, 4 בספטמבר 2010 (IDT) |
| − | + | :::'''אבל איך אתה יכול לדעת שg יכולה להיות מורכבת מפונקציה פסי ומהפונקציה h? ובאותה צורה, איך זה שאתה בוחר "פסי שרירותי" אם אתה קובע שהפסי הזה הוא הרכבה של g ושל f? אשמח לתשובה מפורטת ומובנת הפעם, שלא אצטרך לשבור את הראש כדי לנסות להבין אותה! תודה רבה!''' | |
| − | + | ||
| − | :אם | + | |
| − | + | ::::g יכולה להיות פסי הרכבה h משום שהמקור של פסי צריך להיות פונקציה מB לC ופסי הרכבה h הינה פונקציה מB לC. אני אכן בחרתי פסי שרירותי לא קבעתי שהוא הרכבה של g על f. אני בחרתי פסי שרירותי הראיתי שניתן למצוא לו מקור. מהו אותו מקור? אותו מקור הוא פסי הרכבה h. לכל פונקציה פסי מA לB, התמונה של פסי הרכבה h היא פסי ותמונה של פי מכילה את כל הפונקציות מB לC, דהיינו פי היא על. | |
| − | + | שמע, ידידי, אין לי מושג איך לסייע לך מעבר לכך. כל מה שאני יכול לומר זה שאני ממליץ לך להוכיח כתרגיל שהפונקציה <math>f: \mathbb{Z} \rightarrow \mathbb{Z}</math> שמקיימת לכל <math>x \in \mathbb{Z}</math>, <math>f(x)=x+1</math> היא על, ואז תראה שמבחינה אלגוריתמית אין הבדל בין ההוכחה הזו להוכחה שרשמתי לך למעלה. בהצלחה במבחן! [[משתמש:Adam Chapman|Adam Chapman]] 12:42, 5 בספטמבר 2010 (IDT) | |
| − | + | ==הפרכה בעזרת דוגמה== | |
| + | בתרגיל 2 שאלה 5.ב, למה אי אפשר לתת דוגמה בשביל להפריך טרנזטיביות? הרי אם מראים שקיים B '''מסויים מאוד''' שעבורו אין טרנזטיביות, אז כבר R לא טרנזטיבי...לא? | ||
| − | + | השאלה: http://www.math-wiki.com/images/8/87/10BdidaTargil2.pdf | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | התשובה: http://www.math-wiki.com/images/1/1d/10BdidaTargil2Sol.pdf | |
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | כן. אפשר לעשות גם את זה. אני לא חושב שעבור B ספציפי להראות שאין טרנזיטיביות יותר קצר מלהראות פשוט שאין טרנזיטיביות. מספיקה העובד שB מכיל שני איברים שונים. [[משתמש:Adam Chapman|Adam Chapman]] 19:25, 4 בספטמבר 2010 (IDT) | |
| − | == | + | ==שאלה 1ג מועד א 2008== |
| − | + | שלום רב, | |
| + | האם ההוכחה שלי לשאלה 1ג נכונה? | ||
| − | + | " | |
| + | נניח בשלילה שהחיתוך המתבקש אינו שווה לקבוצה ובה הקבוצה הריקה, ולכן משום שהקבוצה הריקה היא איבר המשותף לכל קבוצות החזקה קיימת קבוצה <math>X\in P(A)</math> ושמקיימת גם <math>X\in P(B)</math> (נשים לב שקבוצה זו שונה מהקבוצה הריקה)....... בסוף נקבל ש- <math>X\subseteq A \bigcap B</math> ולכן החיתוך אינו קבוצה ריקה, וזו סתירה?" | ||
| − | תודה. | + | כמובן שעם פירוט של כל השלבים באמצע. תודה מראש, גל. |
| − | === | + | ===אישור=== |
| − | + | תשובה נכונה בהחלט. [[משתמש:Adam Chapman|Adam Chapman]] 18:52, 4 בספטמבר 2010 (IDT) | |
| − | == | + | ==שאלה== |
| − | + | מהי עוצמת הקבוצה של קבוצות שאינן סופיות ואינן קו-סופיות (שהמשלים שלהן אינו סופי) מתוך הטבעיים? האם זה א כי קבוצה של קבוצות אינסופיות? או לא? תודה! | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | תודה | + | |
===תשובה=== | ===תשובה=== | ||
| − | + | התשובה היא <math>\aleph</math> אך לא כי "קבוצה של קבוצות אינסופיות". | |
| + | הקבוצה <math>\{\mathbb{N},\mathbb{R}\}</math> היא קבוצה של קבוצות אינסופיות המכילה שני איברים בדיוק. | ||
| + | בלי קשר, כפי שלמדנו, המונח "אינסופי" הוא בעל משמעות מאוד רחבה בקורס הזה ולא ניתן להיעזר במונח הזה כדי לטעון אמיתות של תשובה מדוייקת כמו <math>\aleph</math> . | ||
| − | + | העוצמה של הסופיות היא <math>\aleph_0</math> וזו גם העוצמה של הקוסופיות. | |
| − | + | העוצמה של קבוצת החזקה של הטבעיים היא <math>\aleph</math>. | |
| + | אחד מן החוקים שלימדנו אתכם לגבי חשבון עוצמות הוא שכשלוקחים קבוצה אינסופית ומפחיתים ממנה תת-קבוצה בעוצמה קטנה ממש ממנה אז העוצמה לא קטנה, ולכן אחרי שמפחיתים את תת-הקבוצות הסופיות ותת הקבוצות הקוסופיות מכלל תת-הקבוצות של הטבעיים נשארים עם קבוצה שעוצמתה <math>\aleph</math>. [[משתמש:Adam Chapman|Adam Chapman]] 18:45, 4 בספטמבר 2010 (IDT) | ||
| − | + | :למה העוצמה של הסופיות היא <math>\aleph_0</math> וזו גם העוצמה של הקוסופיות? | |
| − | + | ::אהה. הנחתי שאת זה עברנו אם הגענו כבר לשאלה מה הגודל של ההפחתה. OK, אז ככה: | |
| − | + | ||
| − | + | הגודל של תת-הקבוצות בגודל k (סופי) הוא לפחות <math>\aleph_0</math> מצד אחד, ומאידך הוא אינו עולה על <math>\aleph_0^k</math>, ומכיוון שלk סופי מקבלים שמספר תת הקבוצות בגודל k הוא <math>\aleph_0</math>. | |
| + | כעת, קבוצת התת-קבוצות הסופיות היא איחוד זר של קבוצת תת הקבוצות מגודל אחד עם תת הקבוצות מגודל 2 וכו'. דהיינו, הגודל של קבוצת תת הקבוצות הסופיות הוא <math>\aleph_0 \cdot \aleph_0</math>, שזה בעצם (לפי מה שלמדנו) <math>\aleph_0</math>. | ||
| − | + | יש התאמה חח"ע ועל בין הקבוצות הקוסופיות לקבוצות הסופיות ע"י שליחת קבוצה למשלימה, ולכן עוצמת תת הקבוצות הקו-סופיות גם היא <math>\aleph_0</math>.[[משתמש:Adam Chapman|Adam Chapman]] 19:04, 4 בספטמבר 2010 (IDT) | |
| − | + | :תודה רבה!! | |
| − | == | + | ==פרטים בקשר למבחן== |
| − | + | בחלק מהמקומות כתוב שהמבחן ב4 ובחלק 3 וחצי, אפשר שעה (וגם מיקום, אם אפשר) סופיים? תודה! | |
| + | ==הרכבה ריקה== | ||
| + | אם <math>S=\{(a,b)\}</math> ו-<math>R=\{(b,c)\}</math> אז S הרכבה R זו קבוצה ריקה, או "לא קיים"? | ||
===תשובה=== | ===תשובה=== | ||
| − | + | "לא קיים" זה מונח בעייתי. | |
| − | : | + | מונח יותר נכון הוא "לא מוגדר". |
| + | בהינתן יחסים R בין A לB וS בין C לD, ההרכבה <math>S \circ R</math> מוגדרת אם B=C. (כמו בפונקציות) | ||
| + | במקרה שהצגת למעלה אני מניח שהתכוונת שS וR הם יחסים על A כלשהי שמכילה את a, b וc, | ||
| + | ואז התשובה היא באמת קבוצה ריקה. [[משתמש:Adam Chapman|Adam Chapman]] 18:38, 4 בספטמבר 2010 (IDT) | ||
| − | :: | + | ::תודה. אני התכוונתי ש-S יחס מ-A ל-B ו-R יחס מ-B ל-C, אם כך התשובה פה היא לא מוגדר, אם הבנתי נכון. |
| − | + | ::: הבנת נכון.[[משתמש:Adam Chapman|Adam Chapman]] 18:57, 4 בספטמבר 2010 (IDT) | |
| − | == | + | ==סריג== |
| − | + | אפשר בבקשה דוגמה לסריג? | |
| − | + | ||
| − | + | ||
| − | אפשר בבקשה | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
===תשובה=== | ===תשובה=== | ||
| − | + | <math>\{a,b,c,d \}</math> עם היחס סדר חלקי "<" כדלקמן : a>b,a>c,b>d,c>d. | |
| − | + | ||
| − | + | [[משתמש:Adam Chapman|Adam Chapman]] 18:31, 4 בספטמבר 2010 (IDT) | |
| − | + | ||
| − | + | ||
| − | + | :לפי ההגדרה, לכל שני איברים צריך להיות סופרימום ואינפימום. אתה יכול בבקשה לכתוב מהם לכל שני איברים? | |
| − | : | + | ::אם תיקח שני איברים שאחד גדול מהשני תקבל שהסופרימום הוא הגדול בין השנים והאינפימום הוא הקטן בין השניים. הקושיה היחידה שנותרה היא מה קורה בין c לb ובמקרה זה האינפימום הוא d והסופרימום הוא a. [[משתמש:Adam Chapman|Adam Chapman]] 18:56, 4 בספטמבר 2010 (IDT) |
| − | + | :::אה, נראה לי שהבנתי. תודה. אבל "<" הוא לא יחס סדר חלקי, לא? (למשל אין רפלקסיביות) | |
| − | + | ||
| − | + | ::::"<" מעל המספרים הטבעיים הוא יחס סדר מלא (ולכן גם יחס סדר חלקי). פה הוא רק סימון. במקומו יכולתי לרשום R או כל דבר אחר. סתם נוח לי לרשום "<" כי אז ברור מה "כיוון" הסדר (כדי למנוע בלבול מקסימלי-מינימלי).[[משתמש:Adam Chapman|Adam Chapman]] 19:36, 4 בספטמבר 2010 (IDT) | |
| − | + | ||
| − | + | :::::אבל איך? הרי אין רפלקסיביות... | |
| + | ===תשובה לשאלות על התשובה=== | ||
| + | נו! כשכתבתי ">" יחס סדר חלקי התכוונתי שהוא מקיים רפלקסיביות+ את היחסים שרשמתי+את היחסים שמקבלים מתוך היחסים שרשמתי בהינתן הטרנזיטיביות של היחס. | ||
| + | אם אתה רוצה שארשום את כל הזוגות בצורה מפורטת אז הנה: | ||
| + | <math>R=\{(a,a),(b,b),(c,c),(d,d),(b,a),(c,a),(d,a),(d,c),(d,b)\}</math>. | ||
| + | מקווה שזה יסייע להבנה.[[משתמש:Adam Chapman|Adam Chapman]] 19:56, 4 בספטמבר 2010 (IDT) | ||
| − | + | :וואו, זה מבלבל. תודה וסליחה על ההטרחה. | |
| − | + | ==שאלה על אחת השאלות פה== | |
| + | מה זה: "מספר ה'''יחסים''' על קבוצה בעלת n איברים"? מה הכוונה? | ||
| + | :מספר היחסים מA לA (למשל "קטן מ" בקבוצה של מספרים) | ||
| + | ::תודה. הכוונה לכל יחס אפשרי? אז יש אינסוף! למשל: קטן, גדול, מקיים <math>a-b \in Z</math>, מקיים <math>a^2=b</math> ועוד ועוד ועוד... נראה לי שלא הבנתי. | ||
| + | ::ולמה זה הגודל של <math>P(A \times A)</math>? | ||
| − | + | :::העובדה שרשמת שלוש נקודות לא את הופכת הרשימה לאינסופית. יחס, כפי שלמדתם, הוא תת קבוצה של <math>A\times A</math>. הרי בין כל זוג סדור של איברים מהקבוצה יכול להתקיים היחס או לא להתקיים. היחס הוא הקבוצה של כל הזוגות הסדורים בינהם מתקיים היחס. בפרט, כל קבוצה המוכלת ב<math>A\times A</math> מהווה יחס אחד. אוסף כל היחסים הינו אוסף כל תתי הקבוצות הנ"ל וזה בדיוק <math>P(A\times A)</math>. [[משתמש:ארז שיינר|ארז שיינר]] 15:15, 4 בספטמבר 2010 (IDT) | |
| + | ::::אההה.. הבנתי. תודה! (ומה שאני רשמתי הוא אמנם אינסופי, כי למשל <math>a^n=b</math> לכל <math>n \in N</math> הוא יחס נפרד, אבל יש שם יחסים שקולים כי הקבוצה סופית). | ||
| + | :::::בדיוק, ומעל קבוצה אינסופית כמו השלמים בהחלט יש אינסוף יחסים. [[משתמש:ארז שיינר|ארז שיינר]] 15:38, 4 בספטמבר 2010 (IDT) | ||
| − | ==שאלה | + | ==שאלה 3 2008 מועד ב' סעיף ב'== |
| − | + | אני לא מאמין, כתבתי עכשיו עשרות שורות של הפתרון שלי כדי לשאול אם הוא נכון, אבל זה נמחק לי =[. אז פשוט אשאל, אם אפשר, בבקשה, פתרון נכון לשאלה 3 סעיף ב', איזה פונקציה חח"ע ועל אפשר לעשות? זו שאלה קשה אז אני בטוח שיש עוד הרבה שירצו גם פתרון. תודה!! | |
| − | + | :אני גם בדיוק עושה אותה אבל יש לי דרך תיאורטית שאני לא בטוח שהיא נכונה. הרי יודעים שK בין 2 ל2 בחזקת ג, אם מראים שבשני מקרי הקצה של K הוא שווה ל2 בחזקת ג זה לא מספיק כדי להוכיח שוויון תמידי? זה קצת מוזר שלסעיף הזהיש 5 נקודות ולסעיף הראשון יש 10, הוא הרבה יותר קל | |
| − | + | ::מצטערת בשבילך שהכל נמחק, בפעם הבאה אחרי כל כמה שורות תעתיק את כל מה שכתבת ואז תוכל להדביק במקרה הצורך. | |
| − | :אני לא | + | ==שאלה 2 מועד ב' 2008== |
| + | יש לי פתרון אבל אשמח מאם מישהו (עדיף מתרגל) ייתן את הפתרון כדי שאני אהיה בטוח, אני אנסה לכתוב את הפתרון שלי כאן: <math>(-1)^n*{1519-101n \choose 20}</math><math>{1519 \choose 20} + \sum_{n=1}^{14}</math> | ||
| + | שיאללה אני לא מאמין שהצלחתי לכתוב את זה | ||
| + | :אני לא מתרגל, יצא לי דומה לשלך רק שהכנסתי את הגורם הראשון לתוך הסכום, וגם נראה לי שצריך להוסיף כמה פעמים כל חיתוך של קבוצות מופיע, למשל יש 2 מתוך 20 פעמים חיתוך 2 Ai ים (אם עשית את זה בעיקרון הכלה והדחה וצריך לצאת בערך כמו שלך רק עם i מתוך 20 בתוך הסכום | ||
| + | ::כן כן שמתי לב לזה עכשיו, כתבתי את החלק של הכמה יש מתוך בדף אבל התלהבתי כל כך שהצלחתי לכתוב את זה באתר ששכחתי להוסיף, התוצאה שלי היא כזאת: | ||
| + | <math>((-1)^n*{1519-101n \choose 20}*{20 \choose n})</math><math>{1519 \choose 20} + \sum_{n=1}^{14}</math> | ||
| + | האמת שעכשיו אני לא בטוח אם זה צריך להיות <math>{1519-101n \choose 20}</math> או <math>{1519-101n \choose 20-n}</math> | ||
| + | ==איך להוכיח (2008 מועד ב' שאלה 1 א')== | ||
| + | האם אפשר להוכיח ככה, או שיש דרך אחרת? | ||
| + | נניח <math>f(x1,u1)=f(x2,u2)</math> וכן <math>f(x1,u1)={v1 (muchal-be) u1 | x1 (shayach-le) v1}, f(x2,u2)=cmo-x1,u1</math> ולכן לכל V1, V2 שמוכלים בU1, U2 מתקיים V1=V2 ולכן U1=U2 וגם x1=x2? משהו לא נכון בהוכחה הזאת נכון? אז איך מוכיחים? תודה! | ||
| − | + | ===תשובה+הערות כתיבה=== | |
| − | + | 1)אם רוצים לרשום לכתוב "}" אז כותבים }\ ואם רוצים לכתוב "{" אז כותבים {\. | |
| − | אם | + | |
| − | + | ||
| − | + | 2) "מוכל ב" כותבים (כשצד שמאל מוכל בצד ימין) subseteq\ וכשצד ימין מוכל בצד שמאל supseteq\. מוכל ממש זה אותה פקודה רק בלי הeq. | |
| − | + | ||
| + | 3) "שייך" ל רושמים (כשצד שמאל שייך לצד ימין) כin\ וכשצד ימין שייך לשמאל רושמים ni\. | ||
| − | + | עכשיו לגבי התשובה: | |
| − | + | התשובה שלך איננה נכונה משום שאתה מנסה להוכיח טענה שהיא שקרית, דהיינו ניתן לתת לה דוגמאות נגדיות. A כוללת לפחות שני איברים שונים, נסמנם x1 וx2. כעת <math>f(x_1,\{x_2\})=\emptyset=f(x_2,\{x_1\})</math>, משמע f לא חח"ע. | |
| + | [[משתמש:Adam Chapman|Adam Chapman]] 18:54, 4 בספטמבר 2010 (IDT) | ||
| − | == | + | ==שאלות 2א+ב מועד ב 2009== |
| − | + | שלום רב, | |
| + | כיצד עליי לנמק בפתרון השאלה 2א? התחלתי את הפתרון כך: | ||
| − | + | "ישנם <math>n</math> מספרים בקבוצה ולכן סך כל האפשרויות לתמורות שונות הוא <math>n!</math>. כמו כן קיבלנו שתי אפשרויות: | |
| − | + | 1. <math>n</math> לפני <math>n-1</math> | |
| − | + | ||
| − | + | 2. <math>n</math> אחרי <math>n-1</math>" | |
| − | + | השאלה שלי היא איך אני מנמק לאחר מכן שקיימות <math>0.5n!</math> תמורות כנדרש: | |
| − | + | 1. "...לכן לכל תמורה שתי אפשרויות ולכן בסה"כ יש <math>0.5n!</math> תמורות שעונות לתנאי זה". | |
| + | 2. "כעת נגדיר <math>A</math> קבוצת כל התמורות העונות על תנאי 1, <math>B</math> קבוצת כל התמורות העונות על תנאי 2. כמו כן נגדיר פונקציה <math>f:A->B</math> ע"י לכל <math>x</math> ב-<math>A</math> יתקיים ש<math>f(x)=y</math>כאשר <math>y</math> היא התמורה בה איברי <math>x</math> מופיעים בסדר הפוך (כלומר התמורה <math>1,2</math> תהפוך ל-<math>2,1</math>). פונקציה זו חח"ע ועל ולכן <math>|A|=|B|</math> ומכיוון שהחיתוך ביניהם זר הרי שאפשר לומר ש-<math>|A|+|B|=2|A|=|C|</math> (כאשר <math>C</math> היא קבוצת כל התמורות). נציב <math>|C|=n!</math> ונקבל את העוצמה הדרושה של <math>A</math>...". | ||
| − | + | הבעיה היא שדרך 1 נקראית לי לא מפורטת מספיק ודרך 2 היא די ארוכה. בסעיף א זה עוד נסבל אבל בסעיף ב זה בכלל נורא כי כבר קיימות 6 אפשרויות (ואז עליי לבנות 6 פונקציות) אז איך עליי לנמק את מה שאמרתי? | |
| − | + | תודה מראש, גל. | |
| + | ===תשובה=== | ||
| + | אני לא מתרגל אך יש לי את הפתרון שאדם כתב באחד התרגולים שלו. כמו שאמרת, יש סך הכל <math>n!</math> אפשרויות לסדר את המספרים. ניתן לחלק מספר זה של אפשרויות ל2 חלקים: חלק ראשון הוא האפשרויות ש<math>n-1</math> מופיע לפני <math>n</math> והחלק השני הוא ההפוך- <math>n</math> מופיע לפני <math>n-1</math>, ניתן לראות כי 2 חלקים אלה הם שווים, נניח אתה בודק את מספר האפשרויות בהן <math>n-1</math> מופיע לפני <math>n</math>, אז מספר האפשרויות ההפוך הוא אותו מספר כיוון שהפעם החלפת בכל אפשרות בין <math>n</math> ל<math>n-1</math>, ולכן התוצאה היא <math>0.5n!</math>. בסעיף ב' אתה משתמש בתוצאה של סעיף א' ואתה יודע שהיא מתחלקת ל-3 אפשרויות ובאותו אופן כמו בסעיף א' גם 3 אפשרויות אלה הן שוות ולכן בסך הכל התוצאה היא <math>1/6n!</math>. אני שוב אומר שאני לא מתרגל אבל זאת הדרך בה אדם פתר את התרגיל הזה | ||
| − | + | ===הערונת=== | |
| + | אתה מתכוון ל6 אפשרויות ולא שלוש (כל אפשרות שקולה לתמורה על שלושה איברים ומסםר התמורות על 3 איברים הוא 6), ולכן התוצאה שרשמת שהיא שישית ממספר התמורות על n איברים היא נכונה. [[משתמש:Adam Chapman|Adam Chapman]] 18:09, 4 בספטמבר 2010 (IDT) | ||
| − | + | ===תשובה להערונת=== | |
| − | : | + | התכוונתי שיש 3 אפשרויות כאשר יודעים כבר ש<math>n</math> מופיע לפני <math>n-1</math>, 3 אפשרויות אלה הן כאשר <math>n-2</math> מופיע לפני שניהם, בניהם או אחרי שניהם (זה המספר שמחפשים), ובאותו אופן כמו בסעיף הקודם, גם פה 3 האפשרויות האלה שוות, ולכן כל אחת מהן שווה ל<math>1/6n!</math> וסכומן שווה ל<math>0.5n!</math> :) אבל תאכלס אפשר לעשות את זה שוב מההתחלה כשלא מתייחסים לסעיף א' ויש <math>n!</math> אפשרויות סך הכל ואז מחלקים את זה ל!3 אפשרויות שוות, כלומר 6. |
| + | :סבבה, זו גם דרך. רק עשה לי טובה, במקרים כאלה במבחן, אם אתה מניח הנחות יסוד כאלו, כמו שאתה מדבר על "אפשרויות כאשר יודעים כבר ש<math>n</math> מופיע לפני <math>n-1</math>, 3", אז רשום זאת! אל תיתן לבודק לנחש את זה, כי זה עלול להוריד נקודות. מספיק שרשמת את שתי המילים האלו וזה כבר ניקוד מלא. בהצלחה במבחן! [[משתמש:Adam Chapman|Adam Chapman]] 12:48, 5 בספטמבר 2010 (IDT) | ||
| − | + | ==שאלה קצרצרה נוספת== | |
| − | + | מספר היחסים על קבוצה בעלת n איברים, זה בעצם מספר הפונקציות מA לA, כלומר n בחזקת n? או משהו אחר? תודה! | |
| − | ====== | + | ===תשובה=== |
| + | מספר היחסים על קבוצה A בת n איברים היא הגודל של <math>P(A \times A)</math>, שהיינו <math>2^{n^2}</math>. [[משתמש:Adam Chapman|Adam Chapman]] 11:57, 4 בספטמבר 2010 (IDT) | ||
| − | + | ==שאלה קצרה מאוד על עוצמות== | |
| − | + | קבוצת כל הפונקציות מהטבעיים לקבוצת תת הקבוצות של הטבעיים, מהי עוצמתה? לפי החישוב שלי, הקבוצה שווה לP)N( בחזקת N, כלומר העוצמה שווה ל-א בחזקת א0. אך מהי העוצמה א בחזקת א0? א? או יותר, 2 בחזקת א? איך אפשר לדעת את זה? תודה רבה! | |
| − | + | ===תשובה=== | |
| − | + | ישנן כמה נוסחאות לגבי עוצמות אינסופיות שצריך לדעת. אחת מהן היא שאם <math>k</math> אינסופית ו<math>\lambda<k</math> אזי <math>k^\lambda=k</math>. [[משתמש:Adam Chapman|Adam Chapman]] 11:29, 4 בספטמבר 2010 (IDT) | |
| − | :: | + | |
| − | == | + | ==3 שאלות על הרכבת פונקציות== |
| − | + | -אם <math>g*f=Id</math> אז <math>g(f(x))=x</math> או ש <math>f(g(x))=x</math>? כי ניתקלתי בבעיה שקשורה לזה (השאלה השניה). | |
| − | + | -אפשר להגיד ש אם F חחע אז F הפיכה משמאל ואם F על אז היא הפיכה מימין, נכון? | |
| − | + | -איך מוכיחים את מה שצריך להוכיח בשאלה 2 במבחן 2007 מועד א' (http://math-wiki.com/images/4/4f/BdidaExamMoedA2007.pdf) ? | |
| − | + | :ב-א', הוכחתי את הכיוון משמאל לימין, ע"י כך שאם g1*f=g2*f אז בגלל ש'''f הפיכה מימין''' אז נרכיב את f-1 מימין ואז g1=g2. בכיוון השני נתקעתי. | |
| − | + | :ב-ב', לא הצלחתי בכלל. התחלתי ככה: צריך להוכיח שf חחע, כלומר או שנוכיח שאם f(a1)=f(a2) אז a1=a2 או שנוכיח שהיא הפיכה משמאל (לא בטוח מה עדיף). הפונקציה הזאת שמסומנת בסימון של קבוצה ריקה היא על ולכן והפיכה מימין, ולכן O*h=Id ולכן (ופה נתקעתי, לא הייתי בטוח <math>O(h(x))=x</math> ולכן (?) <math>h(x)*f=x</math> ופה יש משהו לא הגיוני. אפשר עזרה? תודה! | |
| − | + | ===תשובה=== | |
| + | אם <math>g*f=Id</math> אז <math>g(f(x))=x</math>. | ||
| + | בקשר לשאלה במבחן הנ"ל, הפיתרון הפשוט (לדעתי) של הסעיף הוא כדלקמן: | ||
| − | + | כיוון אחד | |
| − | 1 | + | 1) אם <math>f</math> חח"ע אזי היא הפיכה משמאל ע"י איזושהי פונקציה שנסמנה <math>h : B \rightarrow A</math>. |
| − | + | ||
| − | = | + | 2) כעת, לכל פונקציה <math>\psi \in C^A</math> יש מקור <math>g=\psi \circ h \in C^B</math> לפי פונקציה <math>\Phi</math>, כי <math>\Phi(g)=g \circ f=\psi \circ h \circ f=\psi</math> ולכן <math>\Phi</math> על. |
| − | + | ||
| − | + | כיוון שני | |
| − | + | 1) אם <math>f</math> לא חח"ע אז קיימים <math>a_1,a_2 \in A</math> שונים כך ש<math>f(a_1)=f(a_2)</math>. | |
| − | + | 2) לכן לכל <math>g \in C^B</math>, הפונקציה <math>\Phi(g)=g \circ f</math> מקיימת <math>g \circ f(a_1)=g \circ f(a_2)</math>. | |
| − | + | 3) אולם, קיימות הפונקציות <math>h \in C^A</math> כך ש<math>h(a_1) \neq h(a_2)</math>, כי <math>C</math> מכילה לפחות שני איברים, וכתצואה מכך <math>\Phi</math> איננה על. | |
| − | == | + | [[משתמש:Adam Chapman|Adam Chapman]] 11:25, 4 בספטמבר 2010 (IDT) |
| − | אם | + | ====אם F חחע אז היא הפיכה '''משמאל''', לא מימין, לא?==== |
| − | + | צודק, רשמתי את ה"הפיכה מימין" כשהתכוונתי להפיכה משמאל, וגם השתמשתי בה כהפיכה משמאל כך שהמילה "ימין" צריכה פשוט להיות מוחלפת ב"משמאל". אשנה זאת מיד.[[מיוחד:תרומות/79.180.9.140|79.180.9.140]] 19:11, 4 בספטמבר 2010 (IDT) | |
| − | + | ||
| − | == | + | ==שאלה (קצת מוזרה, אבל מבלבלת) על איחוד קבוצות== |
| − | + | נניח שX שייך לA חיתוך B חיתוך C. אני יכול להגיד בוודאות ש X שייך ל | |
| − | + | :(AחיתוךBחיתוךC) איחוד (AחיתוךBחיתוךC'(משלים)) איחוד (AחיתוךB'חיתוךC') איחוד (A'חיתוךB'חיתוךC)? האם זה נכון בטוח בגלל שאחד מהגורמים באיחוד הוא A חיתוך B חיתוך C? תודה! | |
===תשובה=== | ===תשובה=== | ||
| − | + | כן. ניתן לומר זאת בודאות כי אחד הגורמים באיחוד הוא הוא A חיתוך B חיתוך C. | |
| − | + | [[משתמש:Adam Chapman|Adam Chapman]] 10:49, 4 בספטמבר 2010 (IDT) | |
| − | + | :תודה רבה אני מאוד מעריך את כל העזרה שלך!! | |
| − | ==שאלה | + | ==עזרה (מבחן 2009 מועד ב' שאלה 7 ב'2 .)== |
| − | + | הוכחתי את 1, ע"י חילוק למקרים, אם C=100 אז A וB יכולים להיות מ1 עד 99, 99 בריבוע אפשרויות, אם C=98 אז יש 98 בריבוע אפשרויות וכך הלאה ומקבלים את הסכום הדרוש. אבל לא משנה איך אני מנסה להסתכל על זה, אני לא רואה איך העוצמה של S שווה לתוצאה שכתובה ב2. אפשר עזרה לפני המבחן? תודה רבה!! | |
| + | ===תשובה=== | ||
| + | את חלק ב' מוכיחים באופן קומבינטורי. כשיש לנו שלישיה סדורה <math>(a,b,c)</math> כך ש<math>a<b \wedge a<c</math> אז קורה אחד (ואחד בלבד) משלושת הדברים הבאים:1) <math>b=c</math> או 2) <math>b<c</math> או 3) <math>b>c</math>. כל המקרים ב1) מכוסים באופן חח"ע ועל על-ידי בחירת שני איברים מתוך 100, הצבת הקטן מבין השניים באינדקס הראשון והצבת הגדול מבין השניים באינדקסים השני והשלישי; כל המקרים ב2) מכוסים באופן חח"ע ועל על-ידי בחירת 3 איברים מתוך מאה, הצבת הקטן ביותר באינדקס הראשון, הצבת האמצעי באינדקס השני והצבת הגדול ביותר באינדקס השלישי; כל המקרים ב3) מכוסים באופן חח"ע ועל על-ידי בחירת 3 איברים מתוך מאה, הצבת הקטןביותר באינדקס הראשון, הצבת הגדול ביותר באינדקס השני והצבת האמצעי באינדקס השלישי. עקב כך, מקבלים את הנוסחה הרשומה בטופס המבחן בסעיף ב'.[[משתמש:Adam Chapman|Adam Chapman]] 10:46, 4 בספטמבר 2010 (IDT) | ||
| + | :תודה | ||
| − | + | ==איחוד או חיתוך== | |
| + | סליחה שאני שואלת המון שאלות.. | ||
| − | + | איך מוכיחים שאם X מוכלת ב-A חיתוך B אז X מוכלת ב-A וגם X מוכלת ב-B? (במיוחד צריך לשים לב שההוכחה לא מתאימה גם לאיחוד במקום חיתוך, בשונה מההוכחה אצלי במחברת) | |
| − | + | ||
| − | + | ||
| + | שוב, תודה מראש! | ||
| − | + | ===שאלות זה טוב=== | |
| + | אם <math>X \subseteq A \bigcap B</math> אז לכל <math>x \in X</math> מתקיים <math>x \in A \bigcap B</math>, דהיינו <math>x \in A</math> וגם <math>x \in B</math>. מכיוון שלכל <math>x \in X</math> מתקיים <math>x \in A</math> אז <math>X \subseteq A</math>, ומכיוון שלכל <math>x \in X</math> מתקיים <math>x \in B</math> אז <math>X \subseteq B</math>. [[משתמש:Adam Chapman|Adam Chapman]] 00:16, 4 בספטמבר 2010 (IDT) | ||
| − | |||
| − | |||
| + | :תודה רבה, אבל: אם <math>X \subseteq A \bigcup B</math> אז לכל <math>x \in X</math> מתקיים <math>x \in A \bigcup B</math>, דהיינו <math>x \in A</math> או <math>x \in B</math>. לכל <math>x \in X</math> מתקיים <math>x \in A</math> ואז*** <math>X \subseteq A</math>, או <math>x \in B</math> ואז*** <math>X \subseteq B</math>. | ||
| + | :מה שמסומן ב-*** כמובן לא נכון, אבל איך מסבירים את זה שהדבר נכון רק עבור חיתוך ולא איחוד? | ||
| − | ''' | + | ::כל <math>x\in X</math> מקיים <math>x\in A</math> '''-או-''' <math>x\in B</math>. בפרט, מאד ייתכן שקיים <math>x\in X</math> כך ש<math>x\notin A</math>. אתה שינית לוגית את המשפט - במקום לומר 'כל איבר שייך לA או B' אמרת 'כל האיברים שייכים לA או כל האיברים שייכים לB'. [[משתמש:ארז שיינר|ארז שיינר]] 01:18, 4 בספטמבר 2010 (IDT) |
| − | + | :::באמת שיניתי לוגית את המשפט בלי לשים לב! אם כך, רק אם '''''לכל''''' <math>x \in X</math> מתקיים <math>x \in A</math> אז <math>X \subseteq A</math>, ובאיחוד זה לא לכל x. הבנתי, תודה לכם! | |
| − | == | + | ==הוכחה טריוויאלית== |
| − | + | מהי הדרך הנכונה ביותר להוכיח שאם <math>P(A)</math> מוכל (או שווה) ב(ל)-<math>P(B)</math> אז A מוכל (או שווה) ב(ל)-B? | |
| + | (פשוט ההוכחה אצלי במחברת לא ברורה לי) | ||
| − | + | ===תשובה=== | |
| + | אם <math>P(A) \subseteq P(B)</math> אז לכל <math>X \in P(A)</math> מתקיים <math>X \in P(B)</math>. | ||
| + | בפרט, <math>A \in P(A)</math> ולכן <math>A \in P(B)</math>, כלומר <math>A \subseteq B</math>. [[משתמש:Adam Chapman|Adam Chapman]] 23:57, 3 בספטמבר 2010 (IDT) | ||
| + | :אהה, תודה! | ||
| − | + | ==יחסים== | |
| + | האם האיבר הקטן ביותר הוא תמיד המינימלי היחיד? (כשהוא קיים) | ||
| − | == | + | ===תשובה=== |
| − | + | כן [[משתמש:Adam Chapman|Adam Chapman]] 23:32, 3 בספטמבר 2010 (IDT) | |
| − | + | :תודה! | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<!------------------------------[שאלות חדשות יש לכתוב בראש הדף, לא בסופו. נא לא לכתוב מתחת לקו זה]------------------------------> | <!------------------------------[שאלות חדשות יש לכתוב בראש הדף, לא בסופו. נא לא לכתוב מתחת לקו זה]------------------------------> | ||
| − | |||
| − | |||
גרסה אחרונה מ־11:30, 3 באוקטובר 2010
תוכן עניינים
- 1 הוראות
- 2 ארכיון
- 3 שאלות
- 3.1 המבחן=
- 3.2 הפגישה
- 3.3 פקטור
- 3.4 חלוקת הציון
- 3.5 ציונים
- 3.6 שאלה חשובה ממבחן
- 3.7 הוכחת יחס בפרט
- 3.8 2007 מועד ב'
- 3.9 מבחן 2007 מועד א'
- 3.10 בקשה לפקטור
- 3.11 שאלות על הפתרון
- 3.12 פתרון המבחן
- 3.13 הצלחה במועד ב'
- 3.14 עוד 2 שאלות קצרות ואחרונות בהחלט!
- 3.15 2 שאלות, אם מתרגל עדיין נמצא פה..
- 3.16 שאלה לסיום
- 3.17 שיבוצי הכיתות
- 3.18 חוקי עוצמות
- 3.19 מתי המבחן?
- 3.20 שאלה 1, סעיף 4 בדף רקורסיה
- 3.21 תרגיל 2
- 3.22 אפשר עזרה בשאלה 3 2008 מועד ב' סעיף ב'?
- 3.23 בעיות ענקיות עם הרכבת פונקציות... -עזרה בבקשה..-
- 3.24 הפרכה בעזרת דוגמה
- 3.25 שאלה 1ג מועד א 2008
- 3.26 שאלה
- 3.27 פרטים בקשר למבחן
- 3.28 הרכבה ריקה
- 3.29 סריג
- 3.30 שאלה על אחת השאלות פה
- 3.31 שאלה 3 2008 מועד ב' סעיף ב'
- 3.32 שאלה 2 מועד ב' 2008
- 3.33 איך להוכיח (2008 מועד ב' שאלה 1 א')
- 3.34 שאלות 2א+ב מועד ב 2009
- 3.35 שאלה קצרצרה נוספת
- 3.36 שאלה קצרה מאוד על עוצמות
- 3.37 3 שאלות על הרכבת פונקציות
- 3.38 שאלה (קצת מוזרה, אבל מבלבלת) על איחוד קבוצות
- 3.39 עזרה (מבחן 2009 מועד ב' שאלה 7 ב'2 .)
- 3.40 איחוד או חיתוך
- 3.41 הוכחה טריוויאלית
- 3.42 יחסים
הוראות
כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:
== כותרת לשאלה ==
לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין
הודעה חשובה !!! - יש להגיש את התרגילים הנוספים (13 , ו 14 כרשות למי שמגיש ) עד ,וכולל , 16.9.2010 ! למשל לתא הבודקת הילה הלוי בכר , או לתומר ביום רביעי או לניר ביום חמישי - בתרגולי החזרה . אנא הודיעו למי שאתם יודעים שלא יגיע לתרגולים אלו . תודה:)
ארכיון
ארכיון 1 - תרגיל 1
ארכיון 2 - תרגיל 2
ארכיון 3 - תרגיל 3
ארכיון 4 - תרגיל 4
ארכיון 5 - לקראת המבחן
שאלות
המבחן=
באיזה בניין וחדר יהיה המועד ב' בבדידה?
הפגישה
באיזה שעה הפגישה והיכן?
פקטור
היה פקטור במבחן?
תשובה
כן
חלוקת הציון
כיצד מחלקים את הציון? כמו בלינארית או שהבוחן ייחשב לכולם? ואם כן באיזה אופן? תודה מראש, גל.
ציונים
מישהו יודע מתי יהיו ציונים?
שאלה חשובה ממבחן
בכמה דרכים ניתן לחלק 40 עטים ממוספרים 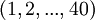 בין 30 סטודנטים?
בין 30 סטודנטים?
לא הבנתי את השאלה:
- האם צריך לחלק את כל ה-40, כך שיהיו 10 סטודנטים שיקבלו 2 עטים? או לחלק רק 30 עטים?
- האם מותר שחלק מהסטודנטים יקבלו 0 עטים? למשל - כל העטים לסטודנט אחד?
אגב, תשובה סופית של השאלה תעזור לי מאוד, בשביל לבדוק את עצמי.
תשובה (לא מתרגל)
כל האפשרויות הללו תופסות. אני הייתי פותר את השאלה כך: עבור כל עט יש שלושים אפשרויות, ולכן בסה"כ יש 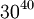 אפשרויות. האם זה פתרון נכון?
אפשרויות. האם זה פתרון נכון?
- אני מניח שהכוונה ל40 עטים ספציפיים, כלומר לא יכול להיות שעט מספר 2 יהיה אצל שני תלמידים.
- נו?תסתכל על זה כך - לעט 1 יש 30 אפשרויות (תלמיד 1 עד תלמיד 30) וגם לעט 2 יש 30 אפשרויות וגם ... וגם לעט 40 יש 30 אפשרויות. ולכן בסה"כ התשובה שציינתי מתקיימת
- צודק, טעות שלי.
הוכחת יחס בפרט
אם נתונה קבוצה B סופית ודי קטנה (כ-5 איברים) ואומרים יהי R יחס על B, הוכיחו ש-R יחס סדר חלקי (או שקילות, לא משנה). האם אני יכולה לכתוב בצורה מפורשת את R ופשוט לכתוב בצורה מפורשת למה היא טרנזטיבית, רפלקסיבית ואנטי סימטרית (או סימטרית), או שאני חייבת לעשות את זה באופן כללי ולא מפורש?
2007 מועד ב'
קישור: http://www.bis.org.il/download_Img.asp?file_name=278200810428508.pdf
בשאלה 1 צריך לרשום בצורת CNF ו-DNF שתי פונקציות שהן ביטוי לוגי. אין לי מושג על מה מדובר, אבל זה לא בחומר - נכון?
שאלה 2 על דטרמיננטות - אני אמורה לדעת לפתור אותה ושאלה דומה יכולה להופיע במבחן מועד ב'? (אני עם אפי, למדנו דטרמיננטות שיעור אחד)
בשאלה 4-ג',ד' ובשאלה 5 צריך להסביר משהו או רק לתת תשובה סופית?
מבחן 2007 מועד א'
קישור: http://www.bis.org.il/download_Img.asp?file_name=208200823203518.pdf
בחלק II שאלה 3 (שצריך להוכיח באינדוקציה), הבדיקה עבור n=1 יצאה לא נכונה! יש טעות בתרגיל או שאני טועה?
בבקשה תענו!
דרך אגב, כל חלק III הוא לא בחומר, נכון?
אה ועוד משהו: יש למישהו פתרונות של המבחן הזה? או לפחות פתרונות סופיים? אם מישהו פתר אותו, אז שיכתוב פה ונשווה :).
במיוחד חשובה לי השאלה בקומבינטוריקה: 1-ב', יצא לי 208.
בקשה לפקטור
המבחן היה ברמה קשה מאוד אז נשמח לקבל פקטור. תודה!
אני בטוח שבגלל שביקשת יהיה פקטור :) (לא שאני מתנגד )
- מצטרפת!
- מצתרף, וזה בלי קשר לבעיות הרבות שהיו, הפסקת חשמל, בעיות בתופס, ועוד.. או לפחות שיקימו מועד מיוחד כדי שהמועד ב' לא תיהיה ההזדמנות האחרונה, זה די מלחיץ, וגם באמת שהתנאים והרמה לא היו בסדר, בהצלחה לכל מי שהולך למועד ב'
שאלות על הפתרון
בשאלה של התמורות, קבעתם את A להיות הקבוצה שבה איבר זוגי מסויים מופיע במקומו, ואז חישבתם את הסכום של כל הקבוצות האלו. אבל זה בעצם החיתוך של המשלימים, אז צריך לעשות את סך כל האפשרויות פחות הסכום שיצא, לא? ולגבי השאלה עם השוויון בין הסיגמות, אתם יכולים לכתוב את הפיתרון? (הוא לא מופיע). תודה!
פתרון המבחן
שלום. אתם יכולים בבקשה לפרסם את הפתרון של המבחן? תודה!
הצלחה במועד ב'
שלום. אני נבחנתי במועד א' ונראה לי שנכשלתי ככה שגם בסופי יהיה לי ציון נכשל. אבל זה בכלל לא אומר שבמהלך כל הקורס ישבתי עם פה פעור ולא הבנתי מילה. עכשיו אני צריכה לגשת למועד ב', ובו אני רוצה להצליח. לא להצליח 80, אלא להצליח 100 לפחות. אני מוכנה לחרוש בשביל זה כמה שצריך, ואפילו יותר. אבל אני רוצה שהחרישה תהיה יעילה כמה שאפשר. אז מתרגלים, בתור מי שהצליחו באיזה קורס או שניים, בבקשה תספרו מנסיונכם, מהי הדרך הכי אפקטיבית ללמוד למבחן? מה ייתן לי את מירב הסיכויים לקבל 100?
תודה מראש!
אני עדיין מחכה לתשובה, בבקשה...
- אני לא בטוח שהם עוד עוכבים אחרי הדף הזה, אבל אולי אם תשאל את השאלה בדף השיחה של אחד המתרגלים הם יענו לך (למשל שיחת משתמש:ארז שיינר ושיחת משתמש:Adam Chapman. את רשימת כל מפעילי המערכת (רובם מתרגלים) תמצא כאן). אור שחף, שיחה, 00:36, 10 בספטמבר 2010 (IDT)
- תודה לך :)
תשובה
- קודם כל יש לוודא שיש לך את כל החומר מההרצאות ושאת מבינה כל דבר ודבר שנעשה בהרצאה (אחר כך כנ"ל לגבי התרגילים)
- יש לעבור על מבחן מועד א' ולוודא שאת מבינה בדיוק איפה טעית, ואיך היית מקבלת 100 אם היית נגשת אליו.
- יש לפתור את כל תרגילי השנה ומבחנים משנים קודמות, דבר ראשון מבלי להסתכל בפתרונות, ולאחר מכן לוודא שפתרת נכון
- תנסי לקבוע שעת קבלה עם המתרגל שלך או מתרגל אחר בקורס שלך (עדיף באמצעות המייל, לא כולם עוקבים אחרי הדף הזה בשלב זה, כמו שאור ציין).
- אני אציין שמה שאמרתי הוא כללי מכיוון שאיני מתרגל בדידה ולכן איני יכול לכוון יותר למקצוע הזה. הכוונה נוספת תוכלי לקבל ממתרגלי בדידה.
בהצלחה,
ארז שיינר 00:52, 10 בספטמבר 2010 (IDT)
- תודה רבה!!
- מבין הדברים שכתבת, משנה מה אעשה קודם ומה אחר כך? ובשביל מה שעת קבלה?
- שעת קבלה לשאול שאלות (אם יש) וגם להתייעץ לגבי הלימודים ספציפית לקורס. לגבי הסדר, אני חושב שנוח לעבוד לפי נושאים הרצאה-תרגול-תרגיל בית (כלומר להבין את ההרצאה בנושא ואז את התרגול בנושא ואז תרגיל בית בנושא ואז לעבור לנושא הבא). אחרי שיש שליטה בחומר עוברים למבחנים ודברים דומים.
עוד 2 שאלות קצרות ואחרונות בהחלט!
יש לי עוד 2 שאלות קצרות שאפשר לענות עליהם עם תשובה סופית בלבד.
- האם
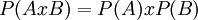 ?
? - נניח A=}1,2,3,{. מספר היחסים על A הוא 2 בחזקת 9 (לפי תשובה לשאלה קודמת), נכון? ומספר יחסים השקילות על A, איך מחשבים את זה? מחשבים אז זה בצורה אחרת, על ידי מספר מחלקות השקילות האפשריות נכון? המחלקות האפשריות הן 1,2,3; 12,3; 1,23; 2,13; 123; כלומר 5? או שיש לי טעות? תודה!
תשובה
התשובה היא לא. 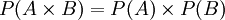 זה שקר ברוב המקרים. אם
זה שקר ברוב המקרים. אם 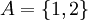 ו
ו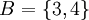 אז
אז 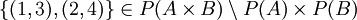 . הכי טוב להבין זאת דרך עוצמות.
. הכי טוב להבין זאת דרך עוצמות. 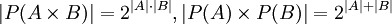 .
.
הוספתי לאחר התנגשות עריכה -לא. נניח בשלילה שזה נכון, אזי:
עיבוד הנוסחה נכשל (שגיאת לקסינג): 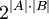
|

|
עיבוד הנוסחה נכשל (שגיאת לקסינג): 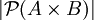
|
||||
קיימות  ו- ו- כך ש: כך ש:
|
עיבוד הנוסחה נכשל (שגיאת לקסינג): 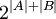
|
עיבוד הנוסחה נכשל (שגיאת לקסינג): 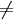
|
||||
עיבוד הנוסחה נכשל (שגיאת לקסינג): 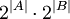
|

|
|||||
עיבוד הנוסחה נכשל (שגיאת לקסינג): 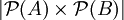
|

|
בסתירה לכך שאם שתי קבוצות שוות אז עוצמתן שווה. אור שחף, שיחה, 14:38, 5 בספטמבר 2010 (IDT)
- תודה! ובקשר לשאלה השנייה, עם מספר היחסים על A, צדקתי או שיש לי טעות? תודה
- לא משנה כבר, בהצלחה!
2 שאלות, אם מתרגל עדיין נמצא פה..
-אם יש נוסחת נסיגה לא הומוגנית, שהאיבר החופשי שלה, במקום להיות מחובר מהצורה 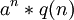 הוא פשוט מספר ללא n, לדוגמה 4, (כלומר: נוסחת נסיגה לדוגמה תהיה an=an-1+an-2+4) מה מציבים בנוסחת הנסיגה? פשוט k ללא n? או 4 בחזקת n כפול k? כי אם מציבים ביטוי ללא n, יש בעיה שהיא- מה להציב בan-1 וכו'.
-אם אפשר עזרה נוספת בנוגעלשאלה הנל, תודה
הוא פשוט מספר ללא n, לדוגמה 4, (כלומר: נוסחת נסיגה לדוגמה תהיה an=an-1+an-2+4) מה מציבים בנוסחת הנסיגה? פשוט k ללא n? או 4 בחזקת n כפול k? כי אם מציבים ביטוי ללא n, יש בעיה שהיא- מה להציב בan-1 וכו'.
-אם אפשר עזרה נוספת בנוגעלשאלה הנל, תודה
תשובה
אם משוואת ההפרשים היא משהו בסגנון 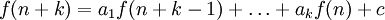 כאשר c הוא קבוע (דהיינו מספר שלא תלוי בn) אז מחפשים פיתרון פרטי של משוואת ההפרשים שיהיה פונקציה קבועה, למשל
כאשר c הוא קבוע (דהיינו מספר שלא תלוי בn) אז מחפשים פיתרון פרטי של משוואת ההפרשים שיהיה פונקציה קבועה, למשל 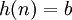 ואז פותרים את המשוואה
ואז פותרים את המשוואה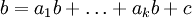 ומקבלים פיתרון
ומקבלים פיתרון 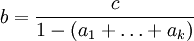 וממשיכים באלגוריתם לפיתרון נוסחת הנסיגה כרגיל. Adam Chapman 12:55, 5 בספטמבר 2010 (IDT)
וממשיכים באלגוריתם לפיתרון נוסחת הנסיגה כרגיל. Adam Chapman 12:55, 5 בספטמבר 2010 (IDT)
- תודה!
עוד אפשרות
אם לא בא לך לזכור את כל המקרים אפשר להפוך את 4 ל- 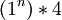
שאלה לסיום
למדנו את הכלל-a כפול b= למקסימום של הערכים. האם אפשר להסיק: תהי k עוצמה. מכפלת k בעצמה שווה לk?
תשובה
ראשית להבהיר, למדנו את המשפט הזה לגבי עוצמות אינסופיות, עבור סופיות כמובן שזה לא עובד. ושנית המכפלה תהיה שווה ל-k רק אם העוצמה קטנה או שווה ל-k
שיבוצי הכיתות
בניין 605
הקבוצה של אפי:
חדר 101: מסטודנט אבני תומר עד מלמד שירן
חדר 102: מסטודנט מרזוק חופית עד שרקנסקי אלה
הקבוצה של שי:
חדר 103: מסטודנט אבוטבול עומר עד כרמל רום
חדר 104: מסטודנט לביא גל עד שרעבי רועי
חוקי עוצמות
אחד החוקים שכתוב לי במחברת הוא שעבור עוצמות a,b,d מתקיים: אם 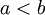 אז
אז 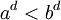 . השאלה היא מהן העוצמות a,b,d, האם זה גם עבור עוצמות סופיות?
. השאלה היא מהן העוצמות a,b,d, האם זה גם עבור עוצמות סופיות?
השאלה היא בהמשך לדוגמה נגדית שמישהו נתן: 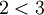 אבל 2 בחזקת א0 שווה 3 בחזקת א0.
אבל 2 בחזקת א0 שווה 3 בחזקת א0.
תשובה
כנראה זה קטן שווה, גם אם d=0 יש שוויון
- כן, כנראה. תודה. בכל מקרה, תשובה חד משמעית ממתרגל תעזור. אולי אפשר ממש להגיד מתי קורה השוויון, ואז להגביל a,b,d כך שהוא לא יקרה אף פעם?
- אני לא מתרגל, אבל לפי דעתי אם זה גדול ממש זה לא תורם יותר מדי, לעומת זאת אם זה גדול שווה זה מראה על קיום פונ' חחע מצד אחד ופונ' על מצד שני.
תשובת מתרגל
אני כן מתרגל, והאמת היא שאם קבוצות מקיימות 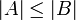 אם ורק אם קיימת פונקצייה על מB ל A שזה קורה אם ורק אם יש פונקצייה חח"ע מA לB. המשמעות של
אם ורק אם קיימת פונקצייה על מB ל A שזה קורה אם ורק אם יש פונקצייה חח"ע מA לB. המשמעות של 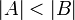 היא שקיימת פונקצייה על מB לA אך לא קיימת פונקצייה על מA לB, שזה קורה אם ורק אם קיימת פונקצייה חח"ע מA לB אך לא קיימת פונקצייה חח"ע מB לA.
בהצלחה במבחן היום! Adam Chapman 12:28, 5 בספטמבר 2010 (IDT)
היא שקיימת פונקצייה על מB לA אך לא קיימת פונקצייה על מA לB, שזה קורה אם ורק אם קיימת פונקצייה חח"ע מA לB אך לא קיימת פונקצייה חח"ע מB לA.
בהצלחה במבחן היום! Adam Chapman 12:28, 5 בספטמבר 2010 (IDT)
- טעות שלי, החוק באמת כתוב עם שווה גם במחברת.
מתי המבחן?
בשלוש וחצי או ארבע? האם התשובה היא ב100 אחוז? תודה!
- בארבע, זה הרי מה שנכתב כאן ובמערכת המידע האישי...
ואיפה?
- שוב, מערכת מידע אישי ולפי מספר קורס 88195 (ולאחר מכן 08 עבור אפי 11 עבור שי) תוכל לראות באיזה חדר אתה משובץ
שאלה 1, סעיף 4 בדף רקורסיה
שלום רב,
אם מבקשים ממני את מספר תתי הקבוצות של 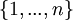 שבהן יש מספרים עוקבים (ביחס רקורסיה), האם מותר לי לפתור כך:
שבהן יש מספרים עוקבים (ביחס רקורסיה), האם מותר לי לפתור כך:
"
עפ"י הסעיף הקודם (סעיף 3) קיבלנו שמספר האפשרויות לתתי הקבוצות של הקבוצה הנתונה בהן אין מספרים עוקבים בכלל הוא 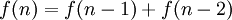 . מכיוון שלכל תת קבוצה יש שתי אפשרויות (שתכיל עוקבים או שלא תכיל עוקביים) ויש בסה"כ
. מכיוון שלכל תת קבוצה יש שתי אפשרויות (שתכיל עוקבים או שלא תכיל עוקביים) ויש בסה"כ 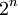 תתי קבוצות אז נגדיר
תתי קבוצות אז נגדיר 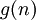 להיות מספר הקבוצות בהן יש מספרים עוקבים ולכן
להיות מספר הקבוצות בהן יש מספרים עוקבים ולכן 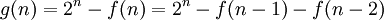 ?"
?"
אם לא, איך אני יכול לפתור? תודה, גל.
תרגיל 2
איפה התשובות של שאלות 8,9? (http://www.math-wiki.com/images/1/1d/10BdidaTargil2Sol.pdf)
אפשר עזרה בשאלה 3 2008 מועד ב' סעיף ב'?
אני כבר ממש מיואש, כל פונקציה שאני בונה יוצאת לא חחע ולא על! זאת שאלה ממש קשה, אבל גם ממש חשובה למבחן, אז אפשר, בבקשה, פתרון או הכוונה? תודה!
תשובה
בשאלה הזו לא מצפים ממך לבנות פונקציה כי אם להשתמש בחוקים אלמנטריים שאתה יודע בחשבון עוצמות. ההוכחה שמצופה מכם היא כזו:
מצד אחד 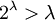 ולכן
ולכן 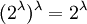 .
מאידך,
.
מאידך, 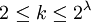 ולכן
ולכן 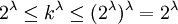 ולכן
ולכן 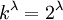 .Adam Chapman 19:33, 4 בספטמבר 2010 (IDT)
.Adam Chapman 19:33, 4 בספטמבר 2010 (IDT)
- אני פשוט לא מאמין, סתם ישבתי לי ובניתי פונקציות..
- בכל מקרה, לא הבנתי אף אחד מהשלבים שעשית! קראתי שוב לאט, ובטוח גם אם הפתרון שלך נכון אז חסר בו פירוט הכרחי באיזשהו מקום- איך אתה יודע שK בחזקת גימל שווה ל2 בחזקת גימל?
- כי
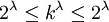
- כי
- לימדו אתכם בהרצאה שאם k אינסופית אזי לכל
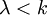 מתקיים
מתקיים 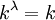 . גם לימדו אתכם בהרצאה שאם עוצמה k קטנה מקיימת
. גם לימדו אתכם בהרצאה שאם עוצמה k קטנה מקיימת 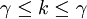 אז
אז 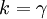 . אלו הם שני החוקים שהשתמשתי בהם בהוכחה הנ"ל. Adam Chapman 19:48, 4 בספטמבר 2010 (IDT)
. אלו הם שני החוקים שהשתמשתי בהם בהוכחה הנ"ל. Adam Chapman 19:48, 4 בספטמבר 2010 (IDT)
- לא!!! התכוונתי לאיך אתה יודע את כל אחד מ2 השלבים האלה! ברור לי שאם אתה יודע שאחד גדול מהשני והשני גדול מהראשון אז על פי קנטור ברנשטיין יש שוויון!!את התוצאה
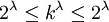 פשוט המצאת. כמו כן פשוט כתבת שאם
פשוט המצאת. כמו כן פשוט כתבת שאם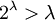 אז
אז 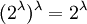 וש
וש 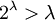 אז
אז 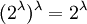 בלי להסביר! מאיפה הבנת את הדברים האלה?? אתה יכול להסביר בבקשה למה K בחזקת גימל גדול מ2 בחזקת גימל ולמה להפך?? תודה
בלי להסביר! מאיפה הבנת את הדברים האלה?? אתה יכול להסביר בבקשה למה K בחזקת גימל גדול מ2 בחזקת גימל ולמה להפך?? תודה
- לא!!! התכוונתי לאיך אתה יודע את כל אחד מ2 השלבים האלה! ברור לי שאם אתה יודע שאחד גדול מהשני והשני גדול מהראשון אז על פי קנטור ברנשטיין יש שוויון!!את התוצאה
- לימדו אתכם בהרצאה שאם k אינסופית אזי לכל
- לימדו בהרצאה שאם k אינסופית אזי לכל
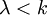 מתקיים
מתקיים 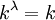 . במשפט הזה תחליף את k ב-
. במשפט הזה תחליף את k ב-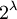 (אינסופי כי
(אינסופי כי  אינסופית נתון). ידוע ש-
אינסופית נתון). ידוע ש- 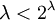 לפי קנטור. לכן לפי המשפט הזה,
לפי קנטור. לכן לפי המשפט הזה, 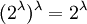 .
.
- לימדו בהרצאה שאם k אינסופית אזי לכל
- חוץ מזה, ידוע שכאשר a,b,c עוצמות: אם a<b, אז
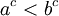 ולכן אם נתון
ולכן אם נתון 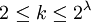 אז
אז 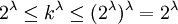 (העלינו הכל בחזקת
(העלינו הכל בחזקת  והשיוויון ממה שהוכחנו קודם). זהו עכשיו לפי קנטור ברנשטיין מ.ש.ל. אגב אני לא מתרגלת אבל מקווה שעזרתי.
והשיוויון ממה שהוכחנו קודם). זהו עכשיו לפי קנטור ברנשטיין מ.ש.ל. אגב אני לא מתרגלת אבל מקווה שעזרתי.
- תודה על העזרה, אדם, אני ממש לא רוצה להעליב, אבל אי אפשר להבין כשישר כותבים תוצאה. אבל נראה לי שיש פה טעות, כי למשל למשפט אם a<b, אז
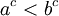 אני יכול לתת דוגמה נגדית. ודבר שני, אני ממש לא זוכר שלמדנו בהרצאה את מה שאת ואדם אמרתם שלמדנו. תודה
אני יכול לתת דוגמה נגדית. ודבר שני, אני ממש לא זוכר שלמדנו בהרצאה את מה שאת ואדם אמרתם שלמדנו. תודה
- תודה על העזרה, אדם, אני ממש לא רוצה להעליב, אבל אי אפשר להבין כשישר כותבים תוצאה. אבל נראה לי שיש פה טעות, כי למשל למשפט אם a<b, אז
- חוץ מזה, ידוע שכאשר a,b,c עוצמות: אם a<b, אז
- איזו דוגמה נגדית? (שים לב ש-c זו עוצמה, לא משלים. הסימונים שהשתמשתי בהם הם לא משהו..) אם אתה עם אפי, אז החוק הזה כתוב לך בעמוד האחרון שלפני קומבינטוריקה (מצחיק, הרגע שמתי לב שכל התרגיל הזה הוא חוק מספר 8 שכתוב שם במדוייק).
- את מה שאדם כתב אין לי במחברת. בכלל, בקושי יש חוקים שלמדנו על עוצמות כלשהן (כשלא ידוע מהי העוצמה). אם הייתה רשימה של כל החוקים האלו זה היה כ-ל-כ-ך עוזר!
- למשל, 2 בחזקת א0 שווה ל3 בחזקת א0, לא?
- וואלה, נראה לי שאתה צודק... אז אולי החוק הזה הוא אם a,b,c עוצמות אינסופיות? לא יודעת. יש איזה מתרגל שיכול לעזור פה?
- למשל, 2 בחזקת א0 שווה ל3 בחזקת א0, לא?
תשובת מתרגל (אע"פ שהתשובת המתרגל כבר רשומה למעלה)
אני מתרגל, ואין לי מושג מי היה המתרגל או המרצה שלכם, חברה, אך נדמה לי שלא רשמתם במחברתכם את כל מה שנאמר בהרצאות או בתרגולים. אני נתתי את רשימת החוקים של חשבון עוצמות גם בתרגול שלי וגם בתרגול העזר של הקורס. שני החוקים שרשמתי למעלה (בפרט הראשון) הם נכונים ונוסחם הוא בדיוק מה שניסחתי לכם למעלה. בהצלחה במבחן! Adam Chapman 12:31, 5 בספטמבר 2010 (IDT)
בעיות ענקיות עם הרכבת פונקציות... -עזרה בבקשה..-
זהו המשך לשאלה ששאלתי קודם, השאלה. אני ממש, ממש תקוע, בסעיף א' כיוון שמאלה, ובסעיף ב' שני הכיוונים (אדם, כנראה שלא הבנתי את הפתרון שלך). למשל ב-ב', אם f חחע, אז לפי מה שהבנתי (וגם בדקתי את זה!) היא הפיכה משמאל ולא מימין. לכן קיימת פו' כך ש hf=id. אבל זה ממש בעייתי ולא עוזר לפתור את הבעיה, כי צריך להוכיח שלכל תמונה של פי, כלומר לכל gf, קיים מקור g, אבל איך אפשר להוכיח את זה, הרי גם אם נרכיב את ההופכי של f משמאל, יצא hgf, שזה לא נותן כלום! מה עושים? (אם אפשר תשובה מפורטת גם לזה וגם לסעיפים\כיוונים האחרים) תודה רבה!
תשובה
אכן הייתה לי טעות בהקלדה אך כדאי שתקרא את התשובה שרשמתי למטה שוב.
עכשיו אולי אוסיף משהו שיסייע להבנה:
אם אתה רוצה להוכיח שפי היא על אתה צריך לקחת איבר בטווח ולהראות שיש לו מקור ,כלומר איזשהו g כך שgf שווה לאיבר בטווח שלקחת. אף אחד לא אומר לך שהאיבר בטווח הוא מן הצורה gf. זה מה שאתה צריך להוכיח!
אתה צריל לקחת איבר כללי בטווח, אותו 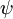 ומראה שקיימת g כך ש
ומראה שקיימת g כך ש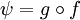 .
זה מה שעשיתי בוהכחה למטה. אני ממליץ לך לקרוא אותה שוב.79.180.9.140 19:16, 4 בספטמבר 2010 (IDT)
.
זה מה שעשיתי בוהכחה למטה. אני ממליץ לך לקרוא אותה שוב.79.180.9.140 19:16, 4 בספטמבר 2010 (IDT)
- לא הבנתי את המשפט:"לכל פונקציה
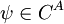 יש מקור
יש מקור 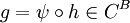 לפי פונקציה
לפי פונקציה 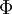 , כי
, כי 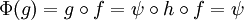 ", באמת שלא הבנתי למה G שווה לפסי הרכבה H ומה זה אומר "לפי פונקציה פי". אפשר הסבר קצת מפורט יותר? תודה!
", באמת שלא הבנתי למה G שווה לפסי הרכבה H ומה זה אומר "לפי פונקציה פי". אפשר הסבר קצת מפורט יותר? תודה!
- אתה צריך להראות שקיימת g כך ש
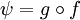 . לא נתונה לך g שאתה צריך להוכיח שהיא
. לא נתונה לך g שאתה צריך להוכיח שהיא 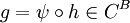 . אתה יכול לבחור איזו g שאתה רוצה. אתה רק צריך להסביר למה אותה g שבחרת היא מקור לפסי. אני בחרתי את g להיות הפונקציה
. אתה יכול לבחור איזו g שאתה רוצה. אתה רק צריך להסביר למה אותה g שבחרת היא מקור לפסי. אני בחרתי את g להיות הפונקציה 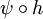 והראיתי שהיא אכן מקור לפסי. מכיוון שפסי הוא שרירותי זה אומר שהראיתי שלכל פסי שרירותי קיים מקור, ולכן פי היא על. כדי להראות שקיים מקור לאיבר אתה צריך לציין את המקור הפוטנציאלי ולהראות שהוא אכן מקור. המקור הוא לא מ שנתון לך. Adam Chapman 19:42, 4 בספטמבר 2010 (IDT)
והראיתי שהיא אכן מקור לפסי. מכיוון שפסי הוא שרירותי זה אומר שהראיתי שלכל פסי שרירותי קיים מקור, ולכן פי היא על. כדי להראות שקיים מקור לאיבר אתה צריך לציין את המקור הפוטנציאלי ולהראות שהוא אכן מקור. המקור הוא לא מ שנתון לך. Adam Chapman 19:42, 4 בספטמבר 2010 (IDT)
- אבל איך אתה יכול לדעת שg יכולה להיות מורכבת מפונקציה פסי ומהפונקציה h? ובאותה צורה, איך זה שאתה בוחר "פסי שרירותי" אם אתה קובע שהפסי הזה הוא הרכבה של g ושל f? אשמח לתשובה מפורטת ומובנת הפעם, שלא אצטרך לשבור את הראש כדי לנסות להבין אותה! תודה רבה!
- אתה צריך להראות שקיימת g כך ש
- g יכולה להיות פסי הרכבה h משום שהמקור של פסי צריך להיות פונקציה מB לC ופסי הרכבה h הינה פונקציה מB לC. אני אכן בחרתי פסי שרירותי לא קבעתי שהוא הרכבה של g על f. אני בחרתי פסי שרירותי הראיתי שניתן למצוא לו מקור. מהו אותו מקור? אותו מקור הוא פסי הרכבה h. לכל פונקציה פסי מA לB, התמונה של פסי הרכבה h היא פסי ותמונה של פי מכילה את כל הפונקציות מB לC, דהיינו פי היא על.
שמע, ידידי, אין לי מושג איך לסייע לך מעבר לכך. כל מה שאני יכול לומר זה שאני ממליץ לך להוכיח כתרגיל שהפונקציה 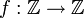 שמקיימת לכל
שמקיימת לכל 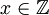 ,
, 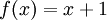 היא על, ואז תראה שמבחינה אלגוריתמית אין הבדל בין ההוכחה הזו להוכחה שרשמתי לך למעלה. בהצלחה במבחן! Adam Chapman 12:42, 5 בספטמבר 2010 (IDT)
היא על, ואז תראה שמבחינה אלגוריתמית אין הבדל בין ההוכחה הזו להוכחה שרשמתי לך למעלה. בהצלחה במבחן! Adam Chapman 12:42, 5 בספטמבר 2010 (IDT)
הפרכה בעזרת דוגמה
בתרגיל 2 שאלה 5.ב, למה אי אפשר לתת דוגמה בשביל להפריך טרנזטיביות? הרי אם מראים שקיים B מסויים מאוד שעבורו אין טרנזטיביות, אז כבר R לא טרנזטיבי...לא?
השאלה: http://www.math-wiki.com/images/8/87/10BdidaTargil2.pdf
התשובה: http://www.math-wiki.com/images/1/1d/10BdidaTargil2Sol.pdf
תשובה
כן. אפשר לעשות גם את זה. אני לא חושב שעבור B ספציפי להראות שאין טרנזיטיביות יותר קצר מלהראות פשוט שאין טרנזיטיביות. מספיקה העובד שB מכיל שני איברים שונים. Adam Chapman 19:25, 4 בספטמבר 2010 (IDT)
שאלה 1ג מועד א 2008
שלום רב, האם ההוכחה שלי לשאלה 1ג נכונה?
"
נניח בשלילה שהחיתוך המתבקש אינו שווה לקבוצה ובה הקבוצה הריקה, ולכן משום שהקבוצה הריקה היא איבר המשותף לכל קבוצות החזקה קיימת קבוצה 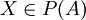 ושמקיימת גם
ושמקיימת גם 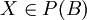 (נשים לב שקבוצה זו שונה מהקבוצה הריקה)....... בסוף נקבל ש-
(נשים לב שקבוצה זו שונה מהקבוצה הריקה)....... בסוף נקבל ש- 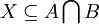 ולכן החיתוך אינו קבוצה ריקה, וזו סתירה?"
ולכן החיתוך אינו קבוצה ריקה, וזו סתירה?"
כמובן שעם פירוט של כל השלבים באמצע. תודה מראש, גל.
אישור
תשובה נכונה בהחלט. Adam Chapman 18:52, 4 בספטמבר 2010 (IDT)
שאלה
מהי עוצמת הקבוצה של קבוצות שאינן סופיות ואינן קו-סופיות (שהמשלים שלהן אינו סופי) מתוך הטבעיים? האם זה א כי קבוצה של קבוצות אינסופיות? או לא? תודה!
תשובה
התשובה היא 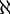 אך לא כי "קבוצה של קבוצות אינסופיות".
הקבוצה
אך לא כי "קבוצה של קבוצות אינסופיות".
הקבוצה 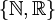 היא קבוצה של קבוצות אינסופיות המכילה שני איברים בדיוק.
בלי קשר, כפי שלמדנו, המונח "אינסופי" הוא בעל משמעות מאוד רחבה בקורס הזה ולא ניתן להיעזר במונח הזה כדי לטעון אמיתות של תשובה מדוייקת כמו
היא קבוצה של קבוצות אינסופיות המכילה שני איברים בדיוק.
בלי קשר, כפי שלמדנו, המונח "אינסופי" הוא בעל משמעות מאוד רחבה בקורס הזה ולא ניתן להיעזר במונח הזה כדי לטעון אמיתות של תשובה מדוייקת כמו 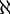 .
.
העוצמה של הסופיות היא 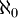 וזו גם העוצמה של הקוסופיות.
העוצמה של קבוצת החזקה של הטבעיים היא
וזו גם העוצמה של הקוסופיות.
העוצמה של קבוצת החזקה של הטבעיים היא 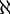 .
אחד מן החוקים שלימדנו אתכם לגבי חשבון עוצמות הוא שכשלוקחים קבוצה אינסופית ומפחיתים ממנה תת-קבוצה בעוצמה קטנה ממש ממנה אז העוצמה לא קטנה, ולכן אחרי שמפחיתים את תת-הקבוצות הסופיות ותת הקבוצות הקוסופיות מכלל תת-הקבוצות של הטבעיים נשארים עם קבוצה שעוצמתה
.
אחד מן החוקים שלימדנו אתכם לגבי חשבון עוצמות הוא שכשלוקחים קבוצה אינסופית ומפחיתים ממנה תת-קבוצה בעוצמה קטנה ממש ממנה אז העוצמה לא קטנה, ולכן אחרי שמפחיתים את תת-הקבוצות הסופיות ותת הקבוצות הקוסופיות מכלל תת-הקבוצות של הטבעיים נשארים עם קבוצה שעוצמתה 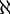 . Adam Chapman 18:45, 4 בספטמבר 2010 (IDT)
. Adam Chapman 18:45, 4 בספטמבר 2010 (IDT)
- למה העוצמה של הסופיות היא
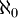 וזו גם העוצמה של הקוסופיות?
וזו גם העוצמה של הקוסופיות?
- אהה. הנחתי שאת זה עברנו אם הגענו כבר לשאלה מה הגודל של ההפחתה. OK, אז ככה:
הגודל של תת-הקבוצות בגודל k (סופי) הוא לפחות 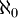 מצד אחד, ומאידך הוא אינו עולה על
מצד אחד, ומאידך הוא אינו עולה על 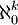 , ומכיוון שלk סופי מקבלים שמספר תת הקבוצות בגודל k הוא
, ומכיוון שלk סופי מקבלים שמספר תת הקבוצות בגודל k הוא 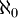 .
כעת, קבוצת התת-קבוצות הסופיות היא איחוד זר של קבוצת תת הקבוצות מגודל אחד עם תת הקבוצות מגודל 2 וכו'. דהיינו, הגודל של קבוצת תת הקבוצות הסופיות הוא
.
כעת, קבוצת התת-קבוצות הסופיות היא איחוד זר של קבוצת תת הקבוצות מגודל אחד עם תת הקבוצות מגודל 2 וכו'. דהיינו, הגודל של קבוצת תת הקבוצות הסופיות הוא 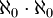 , שזה בעצם (לפי מה שלמדנו)
, שזה בעצם (לפי מה שלמדנו) 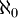 .
.
יש התאמה חח"ע ועל בין הקבוצות הקוסופיות לקבוצות הסופיות ע"י שליחת קבוצה למשלימה, ולכן עוצמת תת הקבוצות הקו-סופיות גם היא 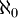 .Adam Chapman 19:04, 4 בספטמבר 2010 (IDT)
.Adam Chapman 19:04, 4 בספטמבר 2010 (IDT)
- תודה רבה!!
פרטים בקשר למבחן
בחלק מהמקומות כתוב שהמבחן ב4 ובחלק 3 וחצי, אפשר שעה (וגם מיקום, אם אפשר) סופיים? תודה!
הרכבה ריקה
אם 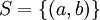 ו-
ו-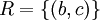 אז S הרכבה R זו קבוצה ריקה, או "לא קיים"?
אז S הרכבה R זו קבוצה ריקה, או "לא קיים"?
תשובה
"לא קיים" זה מונח בעייתי.
מונח יותר נכון הוא "לא מוגדר".
בהינתן יחסים R בין A לB וS בין C לD, ההרכבה 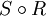 מוגדרת אם B=C. (כמו בפונקציות)
במקרה שהצגת למעלה אני מניח שהתכוונת שS וR הם יחסים על A כלשהי שמכילה את a, b וc,
ואז התשובה היא באמת קבוצה ריקה. Adam Chapman 18:38, 4 בספטמבר 2010 (IDT)
מוגדרת אם B=C. (כמו בפונקציות)
במקרה שהצגת למעלה אני מניח שהתכוונת שS וR הם יחסים על A כלשהי שמכילה את a, b וc,
ואז התשובה היא באמת קבוצה ריקה. Adam Chapman 18:38, 4 בספטמבר 2010 (IDT)
- תודה. אני התכוונתי ש-S יחס מ-A ל-B ו-R יחס מ-B ל-C, אם כך התשובה פה היא לא מוגדר, אם הבנתי נכון.
- הבנת נכון.Adam Chapman 18:57, 4 בספטמבר 2010 (IDT)
- תודה. אני התכוונתי ש-S יחס מ-A ל-B ו-R יחס מ-B ל-C, אם כך התשובה פה היא לא מוגדר, אם הבנתי נכון.
סריג
אפשר בבקשה דוגמה לסריג?
תשובה
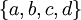 עם היחס סדר חלקי "<" כדלקמן : a>b,a>c,b>d,c>d.
עם היחס סדר חלקי "<" כדלקמן : a>b,a>c,b>d,c>d.
Adam Chapman 18:31, 4 בספטמבר 2010 (IDT)
- לפי ההגדרה, לכל שני איברים צריך להיות סופרימום ואינפימום. אתה יכול בבקשה לכתוב מהם לכל שני איברים?
- אם תיקח שני איברים שאחד גדול מהשני תקבל שהסופרימום הוא הגדול בין השנים והאינפימום הוא הקטן בין השניים. הקושיה היחידה שנותרה היא מה קורה בין c לb ובמקרה זה האינפימום הוא d והסופרימום הוא a. Adam Chapman 18:56, 4 בספטמבר 2010 (IDT)
- אה, נראה לי שהבנתי. תודה. אבל "<" הוא לא יחס סדר חלקי, לא? (למשל אין רפלקסיביות)
- "<" מעל המספרים הטבעיים הוא יחס סדר מלא (ולכן גם יחס סדר חלקי). פה הוא רק סימון. במקומו יכולתי לרשום R או כל דבר אחר. סתם נוח לי לרשום "<" כי אז ברור מה "כיוון" הסדר (כדי למנוע בלבול מקסימלי-מינימלי).Adam Chapman 19:36, 4 בספטמבר 2010 (IDT)
- אבל איך? הרי אין רפלקסיביות...
תשובה לשאלות על התשובה
נו! כשכתבתי ">" יחס סדר חלקי התכוונתי שהוא מקיים רפלקסיביות+ את היחסים שרשמתי+את היחסים שמקבלים מתוך היחסים שרשמתי בהינתן הטרנזיטיביות של היחס.
אם אתה רוצה שארשום את כל הזוגות בצורה מפורטת אז הנה:
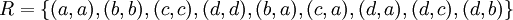 .
מקווה שזה יסייע להבנה.Adam Chapman 19:56, 4 בספטמבר 2010 (IDT)
.
מקווה שזה יסייע להבנה.Adam Chapman 19:56, 4 בספטמבר 2010 (IDT)
- וואו, זה מבלבל. תודה וסליחה על ההטרחה.
שאלה על אחת השאלות פה
מה זה: "מספר היחסים על קבוצה בעלת n איברים"? מה הכוונה?
- מספר היחסים מA לA (למשל "קטן מ" בקבוצה של מספרים)
- תודה. הכוונה לכל יחס אפשרי? אז יש אינסוף! למשל: קטן, גדול, מקיים
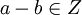 , מקיים
, מקיים 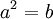 ועוד ועוד ועוד... נראה לי שלא הבנתי.
ועוד ועוד ועוד... נראה לי שלא הבנתי. - ולמה זה הגודל של
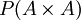 ?
?
- תודה. הכוונה לכל יחס אפשרי? אז יש אינסוף! למשל: קטן, גדול, מקיים
- העובדה שרשמת שלוש נקודות לא את הופכת הרשימה לאינסופית. יחס, כפי שלמדתם, הוא תת קבוצה של
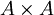 . הרי בין כל זוג סדור של איברים מהקבוצה יכול להתקיים היחס או לא להתקיים. היחס הוא הקבוצה של כל הזוגות הסדורים בינהם מתקיים היחס. בפרט, כל קבוצה המוכלת ב
. הרי בין כל זוג סדור של איברים מהקבוצה יכול להתקיים היחס או לא להתקיים. היחס הוא הקבוצה של כל הזוגות הסדורים בינהם מתקיים היחס. בפרט, כל קבוצה המוכלת ב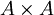 מהווה יחס אחד. אוסף כל היחסים הינו אוסף כל תתי הקבוצות הנ"ל וזה בדיוק
מהווה יחס אחד. אוסף כל היחסים הינו אוסף כל תתי הקבוצות הנ"ל וזה בדיוק 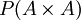 . ארז שיינר 15:15, 4 בספטמבר 2010 (IDT)
. ארז שיינר 15:15, 4 בספטמבר 2010 (IDT)
- אההה.. הבנתי. תודה! (ומה שאני רשמתי הוא אמנם אינסופי, כי למשל
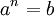 לכל
לכל 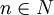 הוא יחס נפרד, אבל יש שם יחסים שקולים כי הקבוצה סופית).
הוא יחס נפרד, אבל יש שם יחסים שקולים כי הקבוצה סופית).
- בדיוק, ומעל קבוצה אינסופית כמו השלמים בהחלט יש אינסוף יחסים. ארז שיינר 15:38, 4 בספטמבר 2010 (IDT)
- אההה.. הבנתי. תודה! (ומה שאני רשמתי הוא אמנם אינסופי, כי למשל
- העובדה שרשמת שלוש נקודות לא את הופכת הרשימה לאינסופית. יחס, כפי שלמדתם, הוא תת קבוצה של
שאלה 3 2008 מועד ב' סעיף ב'
אני לא מאמין, כתבתי עכשיו עשרות שורות של הפתרון שלי כדי לשאול אם הוא נכון, אבל זה נמחק לי =[. אז פשוט אשאל, אם אפשר, בבקשה, פתרון נכון לשאלה 3 סעיף ב', איזה פונקציה חח"ע ועל אפשר לעשות? זו שאלה קשה אז אני בטוח שיש עוד הרבה שירצו גם פתרון. תודה!!
- אני גם בדיוק עושה אותה אבל יש לי דרך תיאורטית שאני לא בטוח שהיא נכונה. הרי יודעים שK בין 2 ל2 בחזקת ג, אם מראים שבשני מקרי הקצה של K הוא שווה ל2 בחזקת ג זה לא מספיק כדי להוכיח שוויון תמידי? זה קצת מוזר שלסעיף הזהיש 5 נקודות ולסעיף הראשון יש 10, הוא הרבה יותר קל
- מצטערת בשבילך שהכל נמחק, בפעם הבאה אחרי כל כמה שורות תעתיק את כל מה שכתבת ואז תוכל להדביק במקרה הצורך.
שאלה 2 מועד ב' 2008
יש לי פתרון אבל אשמח מאם מישהו (עדיף מתרגל) ייתן את הפתרון כדי שאני אהיה בטוח, אני אנסה לכתוב את הפתרון שלי כאן: 
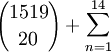 שיאללה אני לא מאמין שהצלחתי לכתוב את זה
שיאללה אני לא מאמין שהצלחתי לכתוב את זה
- אני לא מתרגל, יצא לי דומה לשלך רק שהכנסתי את הגורם הראשון לתוך הסכום, וגם נראה לי שצריך להוסיף כמה פעמים כל חיתוך של קבוצות מופיע, למשל יש 2 מתוך 20 פעמים חיתוך 2 Ai ים (אם עשית את זה בעיקרון הכלה והדחה וצריך לצאת בערך כמו שלך רק עם i מתוך 20 בתוך הסכום
- כן כן שמתי לב לזה עכשיו, כתבתי את החלק של הכמה יש מתוך בדף אבל התלהבתי כל כך שהצלחתי לכתוב את זה באתר ששכחתי להוסיף, התוצאה שלי היא כזאת:
האמת שעכשיו אני לא בטוח אם זה צריך להיות 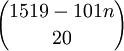 או
או 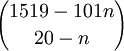
איך להוכיח (2008 מועד ב' שאלה 1 א')
האם אפשר להוכיח ככה, או שיש דרך אחרת?
נניח 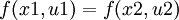 וכן
וכן 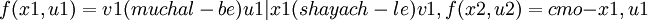 ולכן לכל V1, V2 שמוכלים בU1, U2 מתקיים V1=V2 ולכן U1=U2 וגם x1=x2? משהו לא נכון בהוכחה הזאת נכון? אז איך מוכיחים? תודה!
ולכן לכל V1, V2 שמוכלים בU1, U2 מתקיים V1=V2 ולכן U1=U2 וגם x1=x2? משהו לא נכון בהוכחה הזאת נכון? אז איך מוכיחים? תודה!
תשובה+הערות כתיבה
1)אם רוצים לרשום לכתוב "}" אז כותבים }\ ואם רוצים לכתוב "{" אז כותבים {\.
2) "מוכל ב" כותבים (כשצד שמאל מוכל בצד ימין) subseteq\ וכשצד ימין מוכל בצד שמאל supseteq\. מוכל ממש זה אותה פקודה רק בלי הeq.
3) "שייך" ל רושמים (כשצד שמאל שייך לצד ימין) כin\ וכשצד ימין שייך לשמאל רושמים ni\.
עכשיו לגבי התשובה:
התשובה שלך איננה נכונה משום שאתה מנסה להוכיח טענה שהיא שקרית, דהיינו ניתן לתת לה דוגמאות נגדיות. A כוללת לפחות שני איברים שונים, נסמנם x1 וx2. כעת 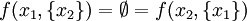 , משמע f לא חח"ע.
Adam Chapman 18:54, 4 בספטמבר 2010 (IDT)
, משמע f לא חח"ע.
Adam Chapman 18:54, 4 בספטמבר 2010 (IDT)
שאלות 2א+ב מועד ב 2009
שלום רב, כיצד עליי לנמק בפתרון השאלה 2א? התחלתי את הפתרון כך:
"ישנם  מספרים בקבוצה ולכן סך כל האפשרויות לתמורות שונות הוא
מספרים בקבוצה ולכן סך כל האפשרויות לתמורות שונות הוא 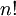 . כמו כן קיבלנו שתי אפשרויות:
. כמו כן קיבלנו שתי אפשרויות:
1.  לפני
לפני 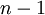
2.  אחרי
אחרי 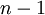 "
"
השאלה שלי היא איך אני מנמק לאחר מכן שקיימות 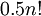 תמורות כנדרש:
תמורות כנדרש:
1. "...לכן לכל תמורה שתי אפשרויות ולכן בסה"כ יש 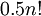 תמורות שעונות לתנאי זה".
תמורות שעונות לתנאי זה".
2. "כעת נגדיר  קבוצת כל התמורות העונות על תנאי 1,
קבוצת כל התמורות העונות על תנאי 1,  קבוצת כל התמורות העונות על תנאי 2. כמו כן נגדיר פונקציה
קבוצת כל התמורות העונות על תנאי 2. כמו כן נגדיר פונקציה 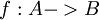 ע"י לכל
ע"י לכל  ב-
ב- יתקיים ש
יתקיים ש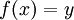 כאשר
כאשר 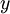 היא התמורה בה איברי
היא התמורה בה איברי  מופיעים בסדר הפוך (כלומר התמורה
מופיעים בסדר הפוך (כלומר התמורה 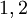 תהפוך ל-
תהפוך ל-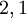 ). פונקציה זו חח"ע ועל ולכן
). פונקציה זו חח"ע ועל ולכן 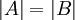 ומכיוון שהחיתוך ביניהם זר הרי שאפשר לומר ש-
ומכיוון שהחיתוך ביניהם זר הרי שאפשר לומר ש-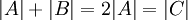 (כאשר
(כאשר 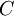 היא קבוצת כל התמורות). נציב
היא קבוצת כל התמורות). נציב 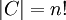 ונקבל את העוצמה הדרושה של
ונקבל את העוצמה הדרושה של  ...".
...".
הבעיה היא שדרך 1 נקראית לי לא מפורטת מספיק ודרך 2 היא די ארוכה. בסעיף א זה עוד נסבל אבל בסעיף ב זה בכלל נורא כי כבר קיימות 6 אפשרויות (ואז עליי לבנות 6 פונקציות) אז איך עליי לנמק את מה שאמרתי? תודה מראש, גל.
תשובה
אני לא מתרגל אך יש לי את הפתרון שאדם כתב באחד התרגולים שלו. כמו שאמרת, יש סך הכל 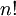 אפשרויות לסדר את המספרים. ניתן לחלק מספר זה של אפשרויות ל2 חלקים: חלק ראשון הוא האפשרויות ש
אפשרויות לסדר את המספרים. ניתן לחלק מספר זה של אפשרויות ל2 חלקים: חלק ראשון הוא האפשרויות ש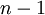 מופיע לפני
מופיע לפני  והחלק השני הוא ההפוך-
והחלק השני הוא ההפוך-  מופיע לפני
מופיע לפני 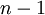 , ניתן לראות כי 2 חלקים אלה הם שווים, נניח אתה בודק את מספר האפשרויות בהן
, ניתן לראות כי 2 חלקים אלה הם שווים, נניח אתה בודק את מספר האפשרויות בהן 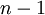 מופיע לפני
מופיע לפני  , אז מספר האפשרויות ההפוך הוא אותו מספר כיוון שהפעם החלפת בכל אפשרות בין
, אז מספר האפשרויות ההפוך הוא אותו מספר כיוון שהפעם החלפת בכל אפשרות בין  ל
ל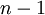 , ולכן התוצאה היא
, ולכן התוצאה היא 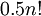 . בסעיף ב' אתה משתמש בתוצאה של סעיף א' ואתה יודע שהיא מתחלקת ל-3 אפשרויות ובאותו אופן כמו בסעיף א' גם 3 אפשרויות אלה הן שוות ולכן בסך הכל התוצאה היא
. בסעיף ב' אתה משתמש בתוצאה של סעיף א' ואתה יודע שהיא מתחלקת ל-3 אפשרויות ובאותו אופן כמו בסעיף א' גם 3 אפשרויות אלה הן שוות ולכן בסך הכל התוצאה היא 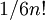 . אני שוב אומר שאני לא מתרגל אבל זאת הדרך בה אדם פתר את התרגיל הזה
. אני שוב אומר שאני לא מתרגל אבל זאת הדרך בה אדם פתר את התרגיל הזה
הערונת
אתה מתכוון ל6 אפשרויות ולא שלוש (כל אפשרות שקולה לתמורה על שלושה איברים ומסםר התמורות על 3 איברים הוא 6), ולכן התוצאה שרשמת שהיא שישית ממספר התמורות על n איברים היא נכונה. Adam Chapman 18:09, 4 בספטמבר 2010 (IDT)
תשובה להערונת
התכוונתי שיש 3 אפשרויות כאשר יודעים כבר ש מופיע לפני
מופיע לפני 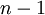 , 3 אפשרויות אלה הן כאשר
, 3 אפשרויות אלה הן כאשר 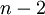 מופיע לפני שניהם, בניהם או אחרי שניהם (זה המספר שמחפשים), ובאותו אופן כמו בסעיף הקודם, גם פה 3 האפשרויות האלה שוות, ולכן כל אחת מהן שווה ל
מופיע לפני שניהם, בניהם או אחרי שניהם (זה המספר שמחפשים), ובאותו אופן כמו בסעיף הקודם, גם פה 3 האפשרויות האלה שוות, ולכן כל אחת מהן שווה ל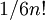 וסכומן שווה ל
וסכומן שווה ל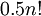 :) אבל תאכלס אפשר לעשות את זה שוב מההתחלה כשלא מתייחסים לסעיף א' ויש
:) אבל תאכלס אפשר לעשות את זה שוב מההתחלה כשלא מתייחסים לסעיף א' ויש 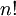 אפשרויות סך הכל ואז מחלקים את זה ל!3 אפשרויות שוות, כלומר 6.
אפשרויות סך הכל ואז מחלקים את זה ל!3 אפשרויות שוות, כלומר 6.
- סבבה, זו גם דרך. רק עשה לי טובה, במקרים כאלה במבחן, אם אתה מניח הנחות יסוד כאלו, כמו שאתה מדבר על "אפשרויות כאשר יודעים כבר ש
 מופיע לפני
מופיע לפני 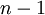 , 3", אז רשום זאת! אל תיתן לבודק לנחש את זה, כי זה עלול להוריד נקודות. מספיק שרשמת את שתי המילים האלו וזה כבר ניקוד מלא. בהצלחה במבחן! Adam Chapman 12:48, 5 בספטמבר 2010 (IDT)
, 3", אז רשום זאת! אל תיתן לבודק לנחש את זה, כי זה עלול להוריד נקודות. מספיק שרשמת את שתי המילים האלו וזה כבר ניקוד מלא. בהצלחה במבחן! Adam Chapman 12:48, 5 בספטמבר 2010 (IDT)
שאלה קצרצרה נוספת
מספר היחסים על קבוצה בעלת n איברים, זה בעצם מספר הפונקציות מA לA, כלומר n בחזקת n? או משהו אחר? תודה!
תשובה
מספר היחסים על קבוצה A בת n איברים היא הגודל של 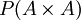 , שהיינו
, שהיינו 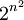 . Adam Chapman 11:57, 4 בספטמבר 2010 (IDT)
. Adam Chapman 11:57, 4 בספטמבר 2010 (IDT)
שאלה קצרה מאוד על עוצמות
קבוצת כל הפונקציות מהטבעיים לקבוצת תת הקבוצות של הטבעיים, מהי עוצמתה? לפי החישוב שלי, הקבוצה שווה לP)N( בחזקת N, כלומר העוצמה שווה ל-א בחזקת א0. אך מהי העוצמה א בחזקת א0? א? או יותר, 2 בחזקת א? איך אפשר לדעת את זה? תודה רבה!
תשובה
ישנן כמה נוסחאות לגבי עוצמות אינסופיות שצריך לדעת. אחת מהן היא שאם 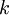 אינסופית ו
אינסופית ו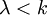 אזי
אזי 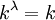 . Adam Chapman 11:29, 4 בספטמבר 2010 (IDT)
. Adam Chapman 11:29, 4 בספטמבר 2010 (IDT)
3 שאלות על הרכבת פונקציות
-אם 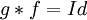 אז
אז 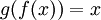 או ש
או ש 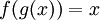 ? כי ניתקלתי בבעיה שקשורה לזה (השאלה השניה).
-אפשר להגיד ש אם F חחע אז F הפיכה משמאל ואם F על אז היא הפיכה מימין, נכון?
-איך מוכיחים את מה שצריך להוכיח בשאלה 2 במבחן 2007 מועד א' (http://math-wiki.com/images/4/4f/BdidaExamMoedA2007.pdf) ?
? כי ניתקלתי בבעיה שקשורה לזה (השאלה השניה).
-אפשר להגיד ש אם F חחע אז F הפיכה משמאל ואם F על אז היא הפיכה מימין, נכון?
-איך מוכיחים את מה שצריך להוכיח בשאלה 2 במבחן 2007 מועד א' (http://math-wiki.com/images/4/4f/BdidaExamMoedA2007.pdf) ?
- ב-א', הוכחתי את הכיוון משמאל לימין, ע"י כך שאם g1*f=g2*f אז בגלל שf הפיכה מימין אז נרכיב את f-1 מימין ואז g1=g2. בכיוון השני נתקעתי.
- ב-ב', לא הצלחתי בכלל. התחלתי ככה: צריך להוכיח שf חחע, כלומר או שנוכיח שאם f(a1)=f(a2) אז a1=a2 או שנוכיח שהיא הפיכה משמאל (לא בטוח מה עדיף). הפונקציה הזאת שמסומנת בסימון של קבוצה ריקה היא על ולכן והפיכה מימין, ולכן O*h=Id ולכן (ופה נתקעתי, לא הייתי בטוח
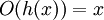 ולכן (?)
ולכן (?) 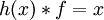 ופה יש משהו לא הגיוני. אפשר עזרה? תודה!
ופה יש משהו לא הגיוני. אפשר עזרה? תודה!
תשובה
אם 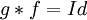 אז
אז 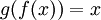 .
.
בקשר לשאלה במבחן הנ"ל, הפיתרון הפשוט (לדעתי) של הסעיף הוא כדלקמן:
כיוון אחד
1) אם  חח"ע אזי היא הפיכה משמאל ע"י איזושהי פונקציה שנסמנה
חח"ע אזי היא הפיכה משמאל ע"י איזושהי פונקציה שנסמנה 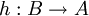 .
.
2) כעת, לכל פונקציה 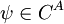 יש מקור
יש מקור 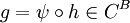 לפי פונקציה
לפי פונקציה 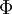 , כי
, כי 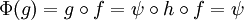 ולכן
ולכן 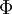 על.
על.
כיוון שני
1) אם  לא חח"ע אז קיימים
לא חח"ע אז קיימים 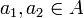 שונים כך ש
שונים כך ש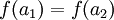 .
.
2) לכן לכל 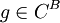 , הפונקציה
, הפונקציה 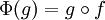 מקיימת
מקיימת 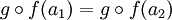 .
.
3) אולם, קיימות הפונקציות 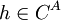 כך ש
כך ש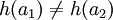 , כי
, כי 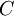 מכילה לפחות שני איברים, וכתצואה מכך
מכילה לפחות שני איברים, וכתצואה מכך 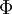 איננה על.
איננה על.
Adam Chapman 11:25, 4 בספטמבר 2010 (IDT)
אם F חחע אז היא הפיכה משמאל, לא מימין, לא?
צודק, רשמתי את ה"הפיכה מימין" כשהתכוונתי להפיכה משמאל, וגם השתמשתי בה כהפיכה משמאל כך שהמילה "ימין" צריכה פשוט להיות מוחלפת ב"משמאל". אשנה זאת מיד.79.180.9.140 19:11, 4 בספטמבר 2010 (IDT)
שאלה (קצת מוזרה, אבל מבלבלת) על איחוד קבוצות
נניח שX שייך לA חיתוך B חיתוך C. אני יכול להגיד בוודאות ש X שייך ל
- (AחיתוךBחיתוךC) איחוד (AחיתוךBחיתוךC'(משלים)) איחוד (AחיתוךB'חיתוךC') איחוד (A'חיתוךB'חיתוךC)? האם זה נכון בטוח בגלל שאחד מהגורמים באיחוד הוא A חיתוך B חיתוך C? תודה!
תשובה
כן. ניתן לומר זאת בודאות כי אחד הגורמים באיחוד הוא הוא A חיתוך B חיתוך C.
Adam Chapman 10:49, 4 בספטמבר 2010 (IDT)
- תודה רבה אני מאוד מעריך את כל העזרה שלך!!
עזרה (מבחן 2009 מועד ב' שאלה 7 ב'2 .)
הוכחתי את 1, ע"י חילוק למקרים, אם C=100 אז A וB יכולים להיות מ1 עד 99, 99 בריבוע אפשרויות, אם C=98 אז יש 98 בריבוע אפשרויות וכך הלאה ומקבלים את הסכום הדרוש. אבל לא משנה איך אני מנסה להסתכל על זה, אני לא רואה איך העוצמה של S שווה לתוצאה שכתובה ב2. אפשר עזרה לפני המבחן? תודה רבה!!
תשובה
את חלק ב' מוכיחים באופן קומבינטורי. כשיש לנו שלישיה סדורה 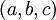 כך ש
כך ש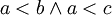 אז קורה אחד (ואחד בלבד) משלושת הדברים הבאים:1)
אז קורה אחד (ואחד בלבד) משלושת הדברים הבאים:1) 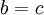 או 2)
או 2) 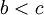 או 3)
או 3) 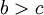 . כל המקרים ב1) מכוסים באופן חח"ע ועל על-ידי בחירת שני איברים מתוך 100, הצבת הקטן מבין השניים באינדקס הראשון והצבת הגדול מבין השניים באינדקסים השני והשלישי; כל המקרים ב2) מכוסים באופן חח"ע ועל על-ידי בחירת 3 איברים מתוך מאה, הצבת הקטן ביותר באינדקס הראשון, הצבת האמצעי באינדקס השני והצבת הגדול ביותר באינדקס השלישי; כל המקרים ב3) מכוסים באופן חח"ע ועל על-ידי בחירת 3 איברים מתוך מאה, הצבת הקטןביותר באינדקס הראשון, הצבת הגדול ביותר באינדקס השני והצבת האמצעי באינדקס השלישי. עקב כך, מקבלים את הנוסחה הרשומה בטופס המבחן בסעיף ב'.Adam Chapman 10:46, 4 בספטמבר 2010 (IDT)
. כל המקרים ב1) מכוסים באופן חח"ע ועל על-ידי בחירת שני איברים מתוך 100, הצבת הקטן מבין השניים באינדקס הראשון והצבת הגדול מבין השניים באינדקסים השני והשלישי; כל המקרים ב2) מכוסים באופן חח"ע ועל על-ידי בחירת 3 איברים מתוך מאה, הצבת הקטן ביותר באינדקס הראשון, הצבת האמצעי באינדקס השני והצבת הגדול ביותר באינדקס השלישי; כל המקרים ב3) מכוסים באופן חח"ע ועל על-ידי בחירת 3 איברים מתוך מאה, הצבת הקטןביותר באינדקס הראשון, הצבת הגדול ביותר באינדקס השני והצבת האמצעי באינדקס השלישי. עקב כך, מקבלים את הנוסחה הרשומה בטופס המבחן בסעיף ב'.Adam Chapman 10:46, 4 בספטמבר 2010 (IDT)
- תודה
איחוד או חיתוך
סליחה שאני שואלת המון שאלות..
איך מוכיחים שאם X מוכלת ב-A חיתוך B אז X מוכלת ב-A וגם X מוכלת ב-B? (במיוחד צריך לשים לב שההוכחה לא מתאימה גם לאיחוד במקום חיתוך, בשונה מההוכחה אצלי במחברת)
שוב, תודה מראש!
שאלות זה טוב
אם 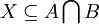 אז לכל
אז לכל 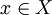 מתקיים
מתקיים 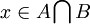 , דהיינו
, דהיינו 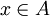 וגם
וגם 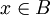 . מכיוון שלכל
. מכיוון שלכל 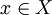 מתקיים
מתקיים 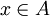 אז
אז 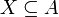 , ומכיוון שלכל
, ומכיוון שלכל 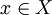 מתקיים
מתקיים 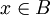 אז
אז 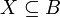 . Adam Chapman 00:16, 4 בספטמבר 2010 (IDT)
. Adam Chapman 00:16, 4 בספטמבר 2010 (IDT)
- תודה רבה, אבל: אם
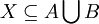 אז לכל
אז לכל 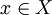 מתקיים
מתקיים 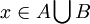 , דהיינו
, דהיינו 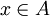 או
או 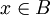 . לכל
. לכל 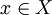 מתקיים
מתקיים 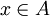 ואז***
ואז*** 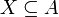 , או
, או 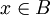 ואז***
ואז*** 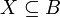 .
. - מה שמסומן ב-*** כמובן לא נכון, אבל איך מסבירים את זה שהדבר נכון רק עבור חיתוך ולא איחוד?
- כל
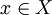 מקיים
מקיים 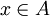 -או-
-או- 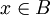 . בפרט, מאד ייתכן שקיים
. בפרט, מאד ייתכן שקיים 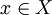 כך ש
כך ש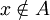 . אתה שינית לוגית את המשפט - במקום לומר 'כל איבר שייך לA או B' אמרת 'כל האיברים שייכים לA או כל האיברים שייכים לB'. ארז שיינר 01:18, 4 בספטמבר 2010 (IDT)
. אתה שינית לוגית את המשפט - במקום לומר 'כל איבר שייך לA או B' אמרת 'כל האיברים שייכים לA או כל האיברים שייכים לB'. ארז שיינר 01:18, 4 בספטמבר 2010 (IDT)
- כל
- באמת שיניתי לוגית את המשפט בלי לשים לב! אם כך, רק אם לכל
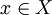 מתקיים
מתקיים 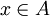 אז
אז 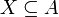 , ובאיחוד זה לא לכל x. הבנתי, תודה לכם!
, ובאיחוד זה לא לכל x. הבנתי, תודה לכם!
- באמת שיניתי לוגית את המשפט בלי לשים לב! אם כך, רק אם לכל
הוכחה טריוויאלית
מהי הדרך הנכונה ביותר להוכיח שאם 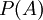 מוכל (או שווה) ב(ל)-
מוכל (או שווה) ב(ל)-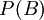 אז A מוכל (או שווה) ב(ל)-B?
אז A מוכל (או שווה) ב(ל)-B?
(פשוט ההוכחה אצלי במחברת לא ברורה לי)
תשובה
אם 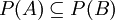 אז לכל
אז לכל 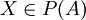 מתקיים
מתקיים 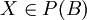 .
בפרט,
.
בפרט, 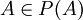 ולכן
ולכן 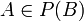 , כלומר
, כלומר 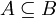 . Adam Chapman 23:57, 3 בספטמבר 2010 (IDT)
. Adam Chapman 23:57, 3 בספטמבר 2010 (IDT)
- אהה, תודה!
יחסים
האם האיבר הקטן ביותר הוא תמיד המינימלי היחיד? (כשהוא קיים)
תשובה
כן Adam Chapman 23:32, 3 בספטמבר 2010 (IDT)
- תודה!