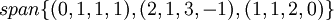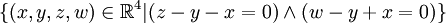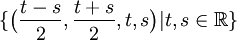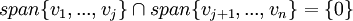הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/5"
(←תרגיל חשוב (חלק מ7.7)) |
(←פתרון) |
||
| (31 גרסאות ביניים של 6 משתמשים אינן מוצגות) | |||
| שורה 44: | שורה 44: | ||
===תכונות === | ===תכונות === | ||
יהיה <math>V</math> מ"ו. יהיו <math>A,B\subseteq V</math> תתי קבוצות ו <math>W,U\leq V</math> תתי מרחבים. אזי | יהיה <math>V</math> מ"ו. יהיו <math>A,B\subseteq V</math> תתי קבוצות ו <math>W,U\leq V</math> תתי מרחבים. אזי | ||
| − | #<math>U+W=span\{U\cup W\}</math>, וכפי שאמרנו הסכום הינו תת המרחב הקטן ביותר המכיל את שני תתי המרחבים. | + | #<math>U+W=span\{U\cup W\}</math>, וכפי שאמרנו הסכום הינו תת המרחב הקטן ביותר המכיל את שני תתי המרחבים. |
| − | + | ||
#<math>A\subseteq span(A)</math> | #<math>A\subseteq span(A)</math> | ||
| − | #<math>span( | + | #<math>A\subseteq B</math> אזי <math>span(A)\subseteq span(B)</math> |
| − | + | # בתירגול הקודם ראינו כי <math>span\{v_1,\dots v_m\}+span\{v_{m+1},\dots v_{m+k}\}=span\{v_1,\dots v_{m+k}\}</math> | |
| − | #מסקנה <math>A\subseteq span(B)</math> | + | ## באופן כללי מתקיים כי <math>span(A)+span(B)=span(A\cup B)</math>. הוכחה: מצד אחד <math>A,B\subseteq A\cup B</math> ולכן <math>span(A),span(B)\subseteq span(A\cup B)</math> ולכן <math>span(A)+span(B)\subseteq span(A\cup B)</math>מצד שני <math>A\subseteq span(A)\subseteq span(A)+span(B)</math> ובאופן דומה גם <math>B\subseteq span(A)+span(B)</math> ולכן <math>A\cup B\subseteq span(A)+span(B)</math> ולכן <math>span(A\cup B)\subseteq span(A)+span(B)</math> |
| + | #<math>span(W)=W</math> (רק אם <math>W</math> ת"מ!) | ||
| + | #מסקנה: אם <math>A\subseteq span(B)</math> אז <math>span(A)\subseteq span(B)</math> (הוכחה: <math>span(A)\subseteq span(span(B))=span(B)</math>) | ||
| + | |||
| + | ==== תרגיל ==== | ||
| + | יהא <math>V</math> מ"ו ויהיו <math>S_{1},S_{2}</math> תתי קבוצות. הוכיחו/הפירכו: | ||
| + | # <math>\sp S_{1}\triangle\sp S_{2}\supseteq\sp\left(S_{1}\triangle S_{2}\right)</math> | ||
| + | # <math>\sp S_{1}\triangle\sp S_{2}\subseteq\sp\left(S_{1}\triangle S_{2}\right)</math> | ||
===תרגילים=== | ===תרגילים=== | ||
| שורה 134: | שורה 140: | ||
\end{array}\right)\}</math> | \end{array}\right)\}</math> | ||
| − | + | הציגו את <math>span(S)</math> ע"י משוואות. מצאו, אם קיים, מטריצה שאינה ב <math>span(S)</math>. האם S בת"ל? | |
| − | + | ||
=====פתרון ===== | =====פתרון ===== | ||
שאלה שקולה: עבור אילו <math>a,b,c,d\in\mathbb{F}</math> קיימים סקלארים <math>\alpha_{1},\alpha_{2},\alpha_{3}</math> כך ש | שאלה שקולה: עבור אילו <math>a,b,c,d\in\mathbb{F}</math> קיימים סקלארים <math>\alpha_{1},\alpha_{2},\alpha_{3}</math> כך ש | ||
| שורה 155: | שורה 160: | ||
| − | נוכל להחליף את המשוואה לעיל | + | נוכל להחליף את המשוואה לעיל במשוואה |
<math>\alpha_{1}\left(\begin{array}{c} | <math>\alpha_{1}\left(\begin{array}{c} | ||
1\\ | 1\\ | ||
| שורה 313: | שורה 318: | ||
==תלות לינארית== | ==תלות לינארית== | ||
| − | |||
| − | |||
| − | |||
הגדרות: | הגדרות: | ||
| שורה 321: | שורה 323: | ||
יהא <math>V</math> מ"ו מעל <math>\mathbb{F}</math>. יהיו וקטורים <math>v_1,...,v_n\in V</math> כלשהם אזי | יהא <math>V</math> מ"ו מעל <math>\mathbb{F}</math>. יהיו וקטורים <math>v_1,...,v_n\in V</math> כלשהם אזי | ||
# ה'''צ"ל הטריוואלי''' הוא צירוף לינארי שכל המקדמים שווים 0 (ואז גם הצירוף שלהם שווה 0). כלומר הצירוף לינארי <math>0v_{1}+0v_{2}+\cdots0v_{n}=0</math> . | # ה'''צ"ל הטריוואלי''' הוא צירוף לינארי שכל המקדמים שווים 0 (ואז גם הצירוף שלהם שווה 0). כלומר הצירוף לינארי <math>0v_{1}+0v_{2}+\cdots0v_{n}=0</math> . | ||
| − | # נאמר ש <math>v_1,...,v_n\in V</math> ''' | + | # נאמר ש <math>v_1,...,v_n\in V</math> '''בלתי תלויים לינארית''' אם אם הצ"ל ה'''יחידי''' שמתאפס הוא הצ"ל הטרוויאלי. באופן שקול אם יש צ"ל שמתאפס אזי הוא הצ"ל הטרוויאלי. ובסימונים: <math>\alpha_{1}v_{1}+\alpha_{2}v_{2}+\cdots\alpha_{n}v_{n}=0 \Rightarrow \forall i \alpha_i = 0</math> |
# <math>v_1,...,v_n\in V</math> יקראו '''תלויים לינארית''' אם הם לא בלתי תלויים לינארית. באופן שקול אם קיימים סקלרים <math>a_1,...,a_n\in\mathbb{F}</math> לא כולם אפס כך שמתקיים <math>a_1v_1+...+a_nv_n=0</math> | # <math>v_1,...,v_n\in V</math> יקראו '''תלויים לינארית''' אם הם לא בלתי תלויים לינארית. באופן שקול אם קיימים סקלרים <math>a_1,...,a_n\in\mathbb{F}</math> לא כולם אפס כך שמתקיים <math>a_1v_1+...+a_nv_n=0</math> | ||
| שורה 327: | שורה 329: | ||
'''הערה:''' הקבוצה הריקה <math>\emptyset \subseteq V</math> מוגדרת כקבוצה בת"ל. | '''הערה:''' הקבוצה הריקה <math>\emptyset \subseteq V</math> מוגדרת כקבוצה בת"ל. | ||
| + | |||
| + | '''הערה/משפט''' תכונה שקולה לכך שקבוצת וקטורים היא תלויה לינארית ניתנת לניסוח באמצעות פרישה. קבוצה S היא ת"ל אמ"מ קיים לפחות וקטור אחד אשר הסרתו מהקבוצה לא פוגעת בspan (כלומר span הקבוצה איתו או בלעדיו שווה). | ||
===דוגמאות === | ===דוגמאות === | ||
| שורה 556: | שורה 560: | ||
אם כן, הצירוף הלינארי היחיד שמתאפס הינו הטריוויאלי ולכן הפולינומים בת"ל. | אם כן, הצירוף הלינארי היחיד שמתאפס הינו הטריוויאלי ולכן הפולינומים בת"ל. | ||
| + | |||
| + | ====דוגמא 6==== | ||
| + | הקבוצה <math>\{1,x,x^2,x^3,\dots \}\subseteq \mathbb{F}[x]</math> היא בת"ל | ||
===משפט=== | ===משפט=== | ||
| שורה 572: | שורה 579: | ||
'''מסקנה:''' אם <math>v_1</math> הינו צירוף לינארי של האחרים ניתן להסיר אותו במובן הבא: <math>span\{v_1,...,v_n\}=span\{v_2,...,v_n\}</math>. | '''מסקנה:''' אם <math>v_1</math> הינו צירוף לינארי של האחרים ניתן להסיר אותו במובן הבא: <math>span\{v_1,...,v_n\}=span\{v_2,...,v_n\}</math>. | ||
| + | ====תרגיל ==== | ||
| + | תרגיל: במרחב <math>V=\mathbb{R}_{2}[x]</math> נגדיר <math>p_{1}(x)=2+6x-5x^{2},p_{2}(x)=1+2x-3x^{2},p_{3}(x)=1-2x-5x^{2}</math> האם <math>p_{1}(x),p_{2}(x),p_{3}(x)</math> בת"ל? אם לא, מצאו צי"ל לא טריוואלי שמתאפס. | ||
| + | |||
| + | ====תרגיל ==== | ||
| + | תרגיל: יהא <math>V</math> מ"ו ויהיו <math>v_{1},v_{2},v_{3}</math> וקטורים. הוכיחו/הפריכו: אם <math>v_{1},v_{2},v_{3}</math> בת"ל בזוגות (כלומר כל זוג וקטורים שונים בת"ל) אזי | ||
| + | <math>\left\{ v_{1},v_{2},v_{3}\right\}</math> בת"ל. | ||
| + | |||
| + | ====תרגיל ==== | ||
| + | תרגיל: יהא V מ"ו ויהיו <math>v_{1},\dots,v_{n}</math> וקטורים. אם <math>v_{1},\dots,v_{n}</math> בת"ל אזי הוקטורים <math>v_{1},v_{2}+v_{1},\dots,v_{n}+v_{1}</math> גם בת"ל. | ||
| + | |||
| + | ====תרגיל ==== | ||
| + | יהא <math>\mathbb{F}^n</math> מ"ו ו <math>A\in\mathbb{F}^{n\times n}</math> מטריצה ריבועית. הוכיחו: (<math>A</math> הפיכה) | ||
| + | אמ"מ (לכל <math>v_{1},\dots,v_{m}</math> בת"ל מתקיים כי <math>Av_{1},\dots,Av_{m}</math> בת"ל.) | ||
| + | |||
| + | ====תרגיל ==== | ||
| + | תרגיל: יהא <math>V=\mathbb{F}^{n\times n}</math> ותהא <math>A\in V</math> הפיכה. הוכיחו/הפריכו: <math>A,A^{2}</math> בת"ל. | ||
===ושוב, בחזרה למערכות משוואות לינאריות=== | ===ושוב, בחזרה למערכות משוואות לינאריות=== | ||
====תרגיל - הקשר בין צירוף לינארי לבין פתרון מערכת משוואות לינאריות===== | ====תרגיל - הקשר בין צירוף לינארי לבין פתרון מערכת משוואות לינאריות===== | ||
| − | יהיו <math> v_1,...,v_n\in \mathbb{F}^m</math> נגדיר <math>A\in mathbb{F}^{m\times n}</math> להיות המטריצה שעמודותיה הן <math> v_1,...,v_n</math> (כלומר <math>C_i(A)=v_i</math>). | + | יהיו <math> v_1,...,v_n\in \mathbb{F}^m</math> נגדיר <math>A\in \mathbb{F}^{m\times n}</math> להיות המטריצה שעמודותיה הן <math> v_1,...,v_n</math> (כלומר <math>C_i(A)=v_i</math>). |
יהיה <math>b\in \mathbb{F}^m</math> וקטור (פתרון). | יהיה <math>b\in \mathbb{F}^m</math> וקטור (פתרון). | ||
| שורה 720: | שורה 743: | ||
טענה: יהיה <math>V</math> מרחב וקטורי מעל <math>\mathbb{F}</math>. תהא <math>S=\{v_{1},\dots v_{n}\}</math> קבוצה ונניח כי קיים <math>i</math> כך ש <math>v_i</math> תלוי באחרים. | טענה: יהיה <math>V</math> מרחב וקטורי מעל <math>\mathbb{F}</math>. תהא <math>S=\{v_{1},\dots v_{n}\}</math> קבוצה ונניח כי קיים <math>i</math> כך ש <math>v_i</math> תלוי באחרים. | ||
| − | אזי <math>span(S)= | + | אזי <math>span(S)=span(S\setminus \{v_i\})</math> |
כמובן שלפעולה זו יש סוף - מתישהו לא ניתן לזרוק אף וקטור מבלי לגרוע מהמרחב הנפרש. הקבוצה שנשארנו איתה תהיה בסיס. | כמובן שלפעולה זו יש סוף - מתישהו לא ניתן לזרוק אף וקטור מבלי לגרוע מהמרחב הנפרש. הקבוצה שנשארנו איתה תהיה בסיס. | ||
| שורה 764: | שורה 787: | ||
(חידה מטופשת: אם ניקח את המימד של צירוף לינארי נקבל מנה טעימה. מהי?) | (חידה מטופשת: אם ניקח את המימד של צירוף לינארי נקבל מנה טעימה. מהי?) | ||
| + | |||
| + | === תרגיל === | ||
| + | מצא בסיס למרחב הפתרונות של המערכת | ||
| + | |||
| + | <math> | ||
| + | \begin{pmatrix} | ||
| + | 1 &-1 &-1 & -1\\ | ||
| + | 1 &1 &-1 &1\\ | ||
| + | \end{pmatrix} | ||
| + | \cdot | ||
| + | \begin{pmatrix} | ||
| + | x_1\\ | ||
| + | x_2\\ | ||
| + | x_3\\ | ||
| + | x_4 | ||
| + | \end{pmatrix} | ||
| + | = 0 | ||
| + | </math> | ||
| + | |||
| + | פתרון: נדרג | ||
| + | |||
| + | <math> | ||
| + | \begin{pmatrix} | ||
| + | 1 &-1 &-1 & -1\\ | ||
| + | 1 &1 &-1 &1 | ||
| + | \end{pmatrix} | ||
| + | \to | ||
| + | \begin{pmatrix} | ||
| + | 1 &-1 &-1 & -1\\ | ||
| + | 0 &2 & 0 & 2\\ | ||
| + | \end{pmatrix} | ||
| + | \to \\ | ||
| + | \begin{pmatrix} | ||
| + | 1 &-1 &-1 & -1\\ | ||
| + | 0 &1 & 0 & 1\\ | ||
| + | \end{pmatrix} | ||
| + | \to | ||
| + | \begin{pmatrix} | ||
| + | 1 &0 &-1 &0\\ | ||
| + | 0 &1 & 0 & 1\\ | ||
| + | \end{pmatrix} | ||
| + | |||
| + | </math> | ||
| + | |||
| + | ולכן הפתרונות הן | ||
| + | |||
| + | <math> | ||
| + | \{ | ||
| + | \begin{pmatrix} | ||
| + | s \\ | ||
| + | -t\\ | ||
| + | s\\ | ||
| + | t | ||
| + | \end{pmatrix} | ||
| + | |||
| + | : t,s\in \mathbb{R} | ||
| + | \} | ||
| + | |||
| + | =span | ||
| + | \{ | ||
| + | \begin{pmatrix} | ||
| + | 1 \\ | ||
| + | 0\\ | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{pmatrix}, | ||
| + | \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | -1\\ | ||
| + | 0\\ | ||
| + | 1 | ||
| + | \end{pmatrix} | ||
| + | |||
| + | \} | ||
| + | |||
| + | </math> | ||
| + | |||
| + | אלו נקראים ה'''פתרונות היסודיים''' והם מהווים בסיס למרחב הפתרונות | ||
| + | |||
| + | === תרגיל === | ||
| + | מצא בסיס לתת המרחב | ||
| + | <math>span | ||
| + | \{\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 2\\ | ||
| + | 1 | ||
| + | \end{array}\right),\left(\begin{array}{c} | ||
| + | -1\\ | ||
| + | -3\\ | ||
| + | 0 | ||
| + | \end{array}\right),\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | -1\\ | ||
| + | 1 | ||
| + | \end{array}\right)\} | ||
| + | </math> | ||
| + | של | ||
| + | <math>V=\mathbb{R}^{3}</math> | ||
| + | |||
| + | פתרון: | ||
| + | |||
| + | כיוון שיש לנו כבר קבוצה פורשת, נותר רק ל"זרוק" את הוקטורים התלויים לינארית. נעשה זאת ע"י ע"י דירוג מטריצה | ||
| + | |||
| + | <math>\left(\begin{array}{ccc} | ||
| + | 1 & -1 & 0\\ | ||
| + | 2 & -3 & -1\\ | ||
| + | 1 & 0 & 1 | ||
| + | \end{array}\right)\to\left(\begin{array}{ccc} | ||
| + | 1 & -1 & 0\\ | ||
| + | 0 & -1 & -1\\ | ||
| + | 0 & 1 & 1 | ||
| + | \end{array}\right)\to\left(\begin{array}{ccc} | ||
| + | 1 & -1 & 0\\ | ||
| + | 0 & 1 & 1\\ | ||
| + | 0 & 0 & 0 | ||
| + | \end{array}\right)\to\left(\begin{array}{ccc} | ||
| + | 1 & 0 & 1\\ | ||
| + | 0 & 1 & 1\\ | ||
| + | 0 & 0 & 0 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | כלומר הוקטור השלישי תלוי לינארית בשניים הראשונים ולכן | ||
| + | |||
| + | <math>span | ||
| + | \{\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 2\\ | ||
| + | 1 | ||
| + | \end{array}\right),\left(\begin{array}{c} | ||
| + | -1\\ | ||
| + | -3\\ | ||
| + | 0 | ||
| + | \end{array}\right),\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | -1\\ | ||
| + | 1 | ||
| + | \end{array}\right)\} | ||
| + | = | ||
| + | span | ||
| + | \{\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 2\\ | ||
| + | 1 | ||
| + | \end{array}\right),\left(\begin{array}{c} | ||
| + | -1\\ | ||
| + | -3\\ | ||
| + | 0 | ||
| + | \end{array}\right) | ||
| + | \} | ||
| + | </math> | ||
| + | |||
| + | וזהו בסיס כי הוקטורים האלה כבר בת"ל | ||
===משפט השלישי חינם=== | ===משפט השלישי חינם=== | ||
| שורה 829: | שורה 1,004: | ||
# <math>B</math> בת"ל. | # <math>B</math> בת"ל. | ||
| − | עפי השלישי חינם, כיוון ש <math>B</math> בת"ל + <math>#B=n=\dim V</math> מתקיים כי <math>span(B)=V</math>. ומכאן ש <math>W=span(B)=V</math> | + | עפי השלישי חינם, כיוון ש <math>B</math> בת"ל + <math>\#B=n=\dim V</math> מתקיים כי <math>span(B)=V</math>. ומכאן ש <math>W=span(B)=V</math> |
'''במילים: תת מרחב שמוכל בתת מרחב אחר מאותו מימד אז הם שווים''' | '''במילים: תת מרחב שמוכל בתת מרחב אחר מאותו מימד אז הם שווים''' | ||
| שורה 843: | שורה 1,018: | ||
התוצאה של תרגיל זה, כאמור, חשובה מאד. אם W תת מרחב של V והוכחנו שהם מאותו המימד זה מספיק על מנת להגיד שהם שווים. אתם תדרשו בעצם לעשות הוכחות כאלה באמצעות מימדים לא פעם ואף לא פעמיים. | התוצאה של תרגיל זה, כאמור, חשובה מאד. אם W תת מרחב של V והוכחנו שהם מאותו המימד זה מספיק על מנת להגיד שהם שווים. אתם תדרשו בעצם לעשות הוכחות כאלה באמצעות מימדים לא פעם ואף לא פעמיים. | ||
| + | |||
| + | ===תרגיל === | ||
| + | יהא <math>V= \mathbb{R}_2[x]</math>. מצא בסיס לחיתוך ובסיס לסכום. | ||
| + | |||
| + | בין <math>W_1 =\{p(x)\in V \; | \; p(1)=0\}</math> | ||
| + | |||
| + | לבין <math>W_2 =\{p(x)\in V \; | \; p(2)=0\}</math> | ||
| + | |||
| + | ==== פתרון ==== | ||
| + | |||
| + | א. '''בסיס לחיתוך:''' החיתוך הוא פשוט <math>W =\{p(x)\in V \; | \; p(1)=p(2)=0\}</math>. | ||
| + | |||
| + | מתקיים כי <math>a_0+a_1x+a_2x^2\in W</math> אמ"מ <math>a_0+a_1+a_2=0=a_0+2a_1+4a_2</math>. | ||
| + | |||
| + | רואים שזהו מערכת משוואות עם משתנה חופשי אחד (המערכת היא 2 משוואות עם 3 נעלמים) ולכן המימד של W הוא 1. | ||
| + | |||
| + | לפי משפט השלישי חינם מספיק למצוא <math>p(x)\in W</math> ואז הוא יהווה בסיס. הנה דוגמא <math>p(x)=(x-1)(x-2)</math>. | ||
| + | |||
| + | ב. '''בסיס לסכום:''' ראשית נציג אותם כנפרשים, ע"י מציאת הפתרונות למשוואות בהגדרת תתי-המרחבים: <math>W_1=span\{-1+x^2,-1+x\},W_2=span\{-4+x^2,-2+x\}</math>. לכן נקבל: <math>W_1+W_2=span\{-1+x^2,-1+x,-4+x^2,-2+x\}</math>, ואז נמצא את הבסיס ע"י למצוא מבין אלה וקטורים שהצ"ל נותן 0 אמ"ם הטריוויאלי, ונקבל ששלושת הראשונים עושים זאת. קיבלנו<math>\dim(W_1+W_2)=3=\dim(\mathbb{R}_2[x])</math>, ולכן <math>W_1+W_2=\mathbb{R}_2[x]</math>. | ||
| + | |||
| + | === תרגיל === | ||
| + | תרגיל: במרחב <math>V=\mathbb{R}^{4}</math>, מצאו בסיס ל <math>W_{1},W_{2}</math> ולסכום ולחיתוך שלהם כאשר | ||
| + | <math>W_{1}=span\left\{ \left(\begin{array}{c} | ||
| + | 2\\ | ||
| + | -1\\ | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right),\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | 1\\ | ||
| + | 0\\ | ||
| + | 1 | ||
| + | \end{array}\right)\right\}</math> | ||
| + | |||
| + | ו <math>W_{2}=\left\{ \left(\begin{array}{c} | ||
| + | a_{1}\\ | ||
| + | a_{2}\\ | ||
| + | a_{3}\\ | ||
| + | a_{4} | ||
| + | \end{array}\right)\mid\begin{array}{c} | ||
| + | a_{1}-3a_{2}-5a_{3}=a_{4}\\ | ||
| + | 4a_{2}+8a_{3}-2a_{4}=2a_{1} | ||
| + | \end{array}\right\}</math> | ||
| + | |||
| + | === תרגיל === | ||
| + | .2 תרגיל: במרחב <math>V=\mathbb{R}_{3}[x]</math>, מצאו בסיס ל <math>W_{1},W_{2}</math> ולסכום ולחיתוך שלהם כאשר | ||
| + | <math>W_{1}=span\left\{ 2-x+x^{2},x+x^{4}\right\}</math> ו <math>W_{2}=\left\{ a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}\mid\begin{array}{c} | ||
| + | a_{0}-3a_{1}-5a_{2}=a_{3}\\ | ||
| + | 4a_{1}+8a_{2}-2a_{3}=2a_{0} | ||
| + | \end{array}\right\}</math> | ||
| + | |||
| + | === תרגיל === | ||
| + | הוכיחו לכל מטריצה <math>A\in\mathbb{F}^{5\times5}</math> מתקיים שהמטריצות <math>\left\{ I,A,A^{2},\dots,A^{25}\right\}</math> ת"ל במרחב <math>V=\mathbb{F}^{n\times n}</math>. | ||
| + | |||
| + | האם קיימת מטריצה <math>A\in\mathbb{F}^{5\times5}</math> כך ש <math>\left\{ I,A,\dots,A^{24}\right\}</math> בת"ל?? (שאלה קשה!) | ||
| + | |||
| + | === תרגיל === | ||
| + | יהא <math>V</math> מ"ו. יהיו <math>W_{1}\subseteq W_{2}</math> תתי מרחבים. הוכיחו/הפירכו: כל בסיס של <math>W_{2}</math> ניתן לצמצום לבסיס של <math>W_{1}</math>. | ||
===תרגיל 7.17=== | ===תרגיל 7.17=== | ||
יהא V מ"ו, ותהא B קבוצה המוכלת בV. הוכח שהתנאים הבאים שקולים: | יהא V מ"ו, ותהא B קבוצה המוכלת בV. הוכח שהתנאים הבאים שקולים: | ||
| − | + | ||
| − | + | (1) <math>B</math> בסיס עבור <math>V</math> | |
| + | |||
| + | (2) וקטור האפס אינו שייך לB ולכל קבוצה <math>A\subseteq B</math> מתקיים <math>V=spanA\oplus span(B/A)</math> | ||
====הוכחה==== | ====הוכחה==== | ||
| − | + | <math>(2) \Leftarrow (1) </math> | |
נניח B בסיס לV, ברור מכך שB בת"ל שהוא אינו מכיל את אפס. תהי A קבוצה המוכלת בB נסמן ב.ה.כ <math>B=\{v_1,...,v_n\}</math> ו <math>A=\{v_1,...,v_j\}</math>. יש להוכיח בעצם שמתקיים <math>V=span\{v_1,...,v_j\}\oplus span\{v_{j+1},...,v_n\} </math>. לצורך זה יש להוכיח שני דברים: | נניח B בסיס לV, ברור מכך שB בת"ל שהוא אינו מכיל את אפס. תהי A קבוצה המוכלת בB נסמן ב.ה.כ <math>B=\{v_1,...,v_n\}</math> ו <math>A=\{v_1,...,v_j\}</math>. יש להוכיח בעצם שמתקיים <math>V=span\{v_1,...,v_j\}\oplus span\{v_{j+1},...,v_n\} </math>. לצורך זה יש להוכיח שני דברים: | ||
| שורה 859: | שורה 1,094: | ||
| − | + | התנאי הראשון: יהא <math>v\in span\{v_1,...,v_j\}\cap span\{v_{j+1},...,v_n\} </math> צ"ל <math>v=0</math>. מהגדרת החיתוך נובע כי קיימים סקלרים כך ש<math>a_1v_1+...+a_jv_j=v=b_{j+1}v_{j+1}+...+b_nv_n</math>. נעביר אגף ונקבל כי <math>a_1v_1+...+a_jv_j-b_{j+1}v_{j+1}-...-b_nv_n=0</math> כיוון ש <math>B</math> בת"ל נובע כי כל המקדמים שווים 0 ובפרט <math>v=0</math> כנדרש. | |
| − | + | התנאי השני: <math>span\{v_1,...,v_j\}+ span\{v_{j+1},...,v_n\}= span\{v_1,...,v_j,v_{j+1},...,v_n \}=span(B)=V</math> | |
| − | + | <math>(1) \Leftarrow (2) </math> | |
מכיוון שזה נכון לכל קבוצה A המוכלת בB, בפרט זה נכון לקבוצה הריקה. לכן יוצא ש <math>V=span\phi\oplus span (B/\phi)=spanB</math> כלומר B פורש את V. נותר להראות שB בת"ל. | מכיוון שזה נכון לכל קבוצה A המוכלת בB, בפרט זה נכון לקבוצה הריקה. לכן יוצא ש <math>V=span\phi\oplus span (B/\phi)=spanB</math> כלומר B פורש את V. נותר להראות שB בת"ל. | ||
נניח בשלילה שB אינה בת"ל, לכן וקטור אחד ממנה u הוא צירוף לינארי של האחרים. נסמן בA את הנקודון שמכיל את u כלומר <math>A=\{u\}</math> ומכייון שבהכרח <math>u \neq 0</math> נקבל סתירה לתכונת הסכום הישר (חיתוך שכולל רק את ווקטור האפס) | נניח בשלילה שB אינה בת"ל, לכן וקטור אחד ממנה u הוא צירוף לינארי של האחרים. נסמן בA את הנקודון שמכיל את u כלומר <math>A=\{u\}</math> ומכייון שבהכרח <math>u \neq 0</math> נקבל סתירה לתכונת הסכום הישר (חיתוך שכולל רק את ווקטור האפס) | ||
גרסה אחרונה מ־19:58, 31 ביולי 2021
תוכן עניינים
צירופים לינאריים והמרחב הנפרש (span)
הגדרה: יהיה  מרחב וקטורי מעל
מרחב וקטורי מעל  . יהיו
. יהיו 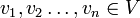 ו
ו 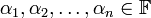 אזי ביטוי מהצורה
אזי ביטוי מהצורה 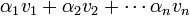 נקרא צירוף לינארי (צ"ל) של
נקרא צירוף לינארי (צ"ל) של 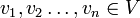 .
.
לדוגמא: 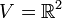 מעל
מעל 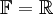 . אזי
. אזי
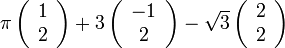
הוא צירוף לינארי.
הגדרה: המרחב הנפרש על ידי הוקטורים 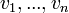 מוגדר להיות קבוצת (אוסף) כל הצירופים הלינאריים של הוקטורים הללו. כלומר,
מוגדר להיות קבוצת (אוסף) כל הצירופים הלינאריים של הוקטורים הללו. כלומר,
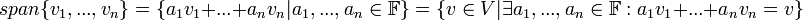 .
.
באופן כללי: תהא 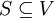 תת קבוצה של מ"ו (ייתכן קבוצה אין סופית) אזי
תת קבוצה של מ"ו (ייתכן קבוצה אין סופית) אזי
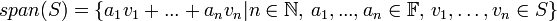
באופן שקול 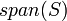 הוא איחוד כל הצירופים הלינאריים של כל תתי הקבוצות הסופיות של
הוא איחוד כל הצירופים הלינאריים של כל תתי הקבוצות הסופיות של  .
.
הערה:
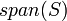 הינו תמיד תת-מרחב כפי שקל להוכיח באמצעות הקריטריון המקוצר - צירוף לינארי של צירופים לינאריים הינו צירוף לינארי בעצמו. בנוסף הוא התת מרחבב הקטן ביותר (מינימום לפי יחס ההכלה) המכיל את הקבוצה אותה הוא פורש
הינו תמיד תת-מרחב כפי שקל להוכיח באמצעות הקריטריון המקוצר - צירוף לינארי של צירופים לינאריים הינו צירוף לינארי בעצמו. בנוסף הוא התת מרחבב הקטן ביותר (מינימום לפי יחס ההכלה) המכיל את הקבוצה אותה הוא פורש
כלומר אם ת"מ 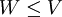 מקיים
מקיים 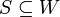 אזי
אזי 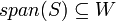
הוכחה
אם 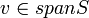 אזי קיימים וקטורים וסקלרים
אזי קיימים וקטורים וסקלרים 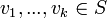 ,
, 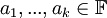 כך שמתקיים
כך שמתקיים 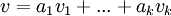 .
מתוך הנתון ש
.
מתוך הנתון ש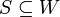 נובע ש
נובע ש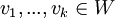 ולכן מתוך סגירות לכפל וסקלר וחיבור
ולכן מתוך סגירות לכפל וסקלר וחיבור 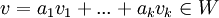 משל.
משל.
הערה: אם 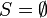 קבוצה ריקה אזי מגדירים פורמאלית כי
קבוצה ריקה אזי מגדירים פורמאלית כי 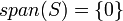
תכונות
יהיה  מ"ו. יהיו
מ"ו. יהיו 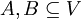 תתי קבוצות ו
תתי קבוצות ו 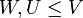 תתי מרחבים. אזי
תתי מרחבים. אזי
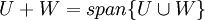 , וכפי שאמרנו הסכום הינו תת המרחב הקטן ביותר המכיל את שני תתי המרחבים.
, וכפי שאמרנו הסכום הינו תת המרחב הקטן ביותר המכיל את שני תתי המרחבים.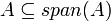
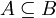 אזי
אזי 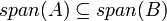
- בתירגול הקודם ראינו כי
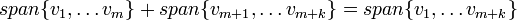
- באופן כללי מתקיים כי
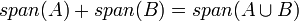 . הוכחה: מצד אחד
. הוכחה: מצד אחד 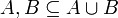 ולכן
ולכן 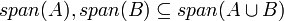 ולכן
ולכן 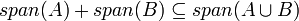 מצד שני
מצד שני 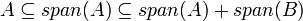 ובאופן דומה גם
ובאופן דומה גם 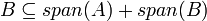 ולכן
ולכן 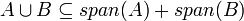 ולכן
ולכן 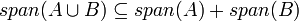
- באופן כללי מתקיים כי
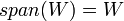 (רק אם
(רק אם 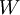 ת"מ!)
ת"מ!) - מסקנה: אם
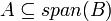 אז
אז 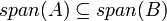 (הוכחה:
(הוכחה: 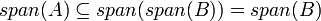 )
)
תרגיל
יהא  מ"ו ויהיו
מ"ו ויהיו 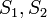 תתי קבוצות. הוכיחו/הפירכו:
תתי קבוצות. הוכיחו/הפירכו:
- עיבוד הנוסחה נכשל (פונקציה \sp לא מוכרת): \sp S_{1}\triangle\sp S_{2}\supseteq\sp\left(S_{1}\triangle S_{2}\right)
- עיבוד הנוסחה נכשל (פונקציה \sp לא מוכרת): \sp S_{1}\triangle\sp S_{2}\subseteq\sp\left(S_{1}\triangle S_{2}\right)
תרגילים
תרגיל 1
במרחב הוקטורי 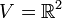 מעל
מעל 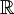 נגדיר
נגדיר
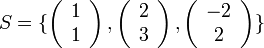
מצא עבור אילו 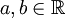 מתקיים כי
מתקיים כי
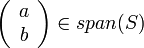
פתרון
שאלה שקולה: עבור אילו 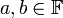 קיימים סקלארים
קיימים סקלארים 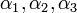 כך ש
כך ש
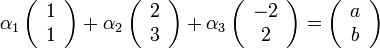
שזה בעצם לשאול האם למערכת
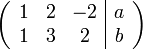 יש פתרון.
יש פתרון.
נדרג ונבדוק
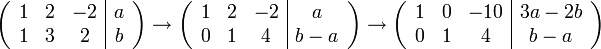
כלומר יש פתרון למערכת (אפילו אינסוף פתרונות) ולכן לכל
 מתקיים כי
מתקיים כי
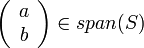
כלומר 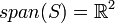
תרגיל 2
במרחב הוקטורי 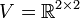 מעל
מעל 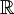 נגדיר
נגדיר
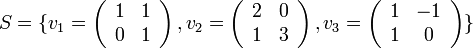
הציגו את 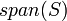 ע"י משוואות. מצאו, אם קיים, מטריצה שאינה ב
ע"י משוואות. מצאו, אם קיים, מטריצה שאינה ב 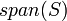 . האם S בת"ל?
. האם S בת"ל?
פתרון
שאלה שקולה: עבור אילו 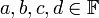 קיימים סקלארים
קיימים סקלארים 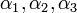 כך ש
כך ש
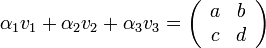
אם נייצג כל מטריצה באמצעות וקטור. למשל
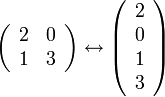
נוכל להחליף את המשוואה לעיל במשוואה
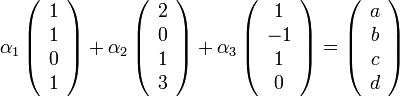
(שימו לב שאלו בדיוק אותם ארבעת המשוואות).
כעת נוכל פשוט לשאול האם למערכת
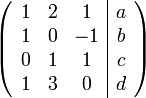 יש פתרון
יש פתרון
נדרג ונבדוק:
עיבוד הנוסחה נכשל (שגיאת תחביר): \left(\begin{array}{ccc|c} 1 & 2 & 1 & a\\ 1 & 0 & -1 & b\\ 0 & 1 & 1 & c\\ 1 & 3 & 0 & d \end{array}\right)\to\left(\begin{array}{ccc|c} 1 & 0 & -1 & b\\ 0 & 1 & 1 & c\\ 1 & 3 & 0 & d\\ 1 & 2 & 1 & a \end{array}\right)\to\\\left(\begin{array}{ccc|c} 1 & 0 & -1 & b\\ 0 & 1 & 1 & c\\ 0 & 3 & 1 & d-b\\ 0 & 2 & 2 & a-b \end{array}\right)\to\left(\begin{array}{ccc|c} 1 & 0 & -1 & b\\ 0 & 1 & 1 & c\\ 0 & 0 & -2 & d-b-3c\\ 0 & 0 & 0 & a-b-2c \end{array}\right)
רואים שיש פתרון אמ"מ 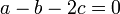
לכן התשובה הסופית היא
עיבוד הנוסחה נכשל (שגיאת תחביר): span(S)=\{\left(\begin{array}{cc} a & b\\ c & d \end{array}\right)\,|\,a-b-2c=0\}= \{\left(\begin{array}{cc} b+2c & b\\ c & d \end{array}\right)\,|\,b,c,d\in \mathbb{R}\} = \\ \{ b\left(\begin{array}{cc} 1 & 1\\ 0 & 0 \end{array}\right)+c\left(\begin{array}{cc} 2 & 0\\ 1 & 0 \end{array}\right)+d\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \,|\,b,c,d\in \mathbb{R}\} = span\{\left(\begin{array}{cc} 1 & 1\\ 0 & 0 \end{array}\right),\left(\begin{array}{cc} 2 & 0\\ 1 & 0 \end{array}\right),\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right)\}
כמו שרואים בפתרון הסופי, ניתן להביע את התת מרחב שלנו בכמה צורות.
הנה עוד דוגמא
הערה: ניתן להגדיר/להציג תת מרחב בכמה דרכים
בסעיף זה נראה מספר הצגות לאותו תת מרחב נראה שישנן שלוש דרכים שונות להציג את אותו תת המרחב הוקטורי.
תרגיל.
יהי 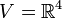 , הוכח ששלוש הקבוצות הבאות שוות:
, הוכח ששלוש הקבוצות הבאות שוות:
פתרון:
נראה שהקבוצה הראשונה שווה לשנייה. וקטור נמצא בspan של קבוצת הוקטורים אם"ם הוא צירוף לינארי שלה. לכן, 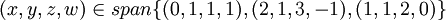 אם"ם קיימים סקלרים a,b,c כך ש
אם"ם קיימים סקלרים a,b,c כך ש 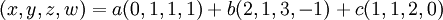 . לכן, הוקטור הוא צ"ל אם"ם קיים פתרון למערכת המשוואות הלינארית על a,b,c כאלה. בעצם, אנו רוצים לאמר על מערכת משוואות פרמטרית מתי יש לה פתרון. נביט במערכת המשוואות:
. לכן, הוקטור הוא צ"ל אם"ם קיים פתרון למערכת המשוואות הלינארית על a,b,c כאלה. בעצם, אנו רוצים לאמר על מערכת משוואות פרמטרית מתי יש לה פתרון. נביט במערכת המשוואות:
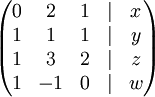
נדרג את המערכת לקבל
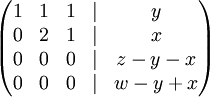
זכרו שלא מעניין אותנו פתרון המערכת, שכן אלו הסקלרים של הצירוף הלינארי. מה שמעניין אותנו הוא האם קיים פתרון למערכת ובמקרה זה קיים פתרון אם"ם 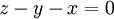 וגם
וגם 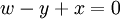 וזו בדיוק הקבוצה השנייה.
וזו בדיוק הקבוצה השנייה.
(שימו לב גם למשפט מתרגול שעבר - b נמצא במרחב העמודות של A אם ורק אם למערכת Ax=b יש פתרון. זה בדיוק מה שקיבלנו בתרגיל זה.)
כעת נראה את השיוויון בין הקבוצה השנייה לשלישית. המרחב הוא בעצם אוסף הפתרונות של מערכת המשוואות הלינארית הנתונה. נדרג אותה והפעם נחפש את הפתרון הכללי.
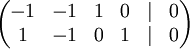
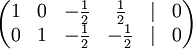
יש שני משתנים תלויים- x,y ושני משתנים חופשיים- z,w. נסמן z=t, w=s ונקבל פתרון כללי מהצורה 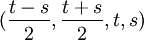
תלות לינארית
הגדרות:
יהא  מ"ו מעל
מ"ו מעל  . יהיו וקטורים
. יהיו וקטורים 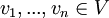 כלשהם אזי
כלשהם אזי
- הצ"ל הטריוואלי הוא צירוף לינארי שכל המקדמים שווים 0 (ואז גם הצירוף שלהם שווה 0). כלומר הצירוף לינארי
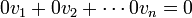 .
. - נאמר ש
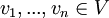 בלתי תלויים לינארית אם אם הצ"ל היחידי שמתאפס הוא הצ"ל הטרוויאלי. באופן שקול אם יש צ"ל שמתאפס אזי הוא הצ"ל הטרוויאלי. ובסימונים:
בלתי תלויים לינארית אם אם הצ"ל היחידי שמתאפס הוא הצ"ל הטרוויאלי. באופן שקול אם יש צ"ל שמתאפס אזי הוא הצ"ל הטרוויאלי. ובסימונים: 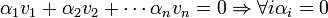
-
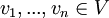 יקראו תלויים לינארית אם הם לא בלתי תלויים לינארית. באופן שקול אם קיימים סקלרים
יקראו תלויים לינארית אם הם לא בלתי תלויים לינארית. באופן שקול אם קיימים סקלרים 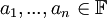 לא כולם אפס כך שמתקיים
לא כולם אפס כך שמתקיים 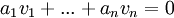
הגדרה (הכלל): קבוצה 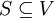 נקראת תלוייה לינארית אם קיימת בתוכה קבוצה סופית כלשהי של וקטורים, כך שוקטוריה תלויים לינארית לפי ההגדרה לעיל. [לא נתעסק בקורס זה בקבוצת אינסופיות בת"ל, אבל אתם יותר ממוזמנים לנסות לחשוב על מרחב וקטורי בעל קבוצה אינסופית בת"ל של וקטורים.]
נקראת תלוייה לינארית אם קיימת בתוכה קבוצה סופית כלשהי של וקטורים, כך שוקטוריה תלויים לינארית לפי ההגדרה לעיל. [לא נתעסק בקורס זה בקבוצת אינסופיות בת"ל, אבל אתם יותר ממוזמנים לנסות לחשוב על מרחב וקטורי בעל קבוצה אינסופית בת"ל של וקטורים.]
הערה: הקבוצה הריקה 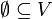 מוגדרת כקבוצה בת"ל.
מוגדרת כקבוצה בת"ל.
הערה/משפט תכונה שקולה לכך שקבוצת וקטורים היא תלויה לינארית ניתנת לניסוח באמצעות פרישה. קבוצה S היא ת"ל אמ"מ קיים לפחות וקטור אחד אשר הסרתו מהקבוצה לא פוגעת בspan (כלומר span הקבוצה איתו או בלעדיו שווה).
דוגמאות
דוגמא 1
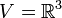 מעל
מעל 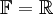
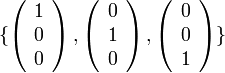 בת"ל כי
בת"ל כי
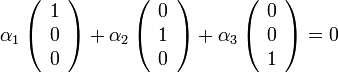
פירושו
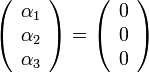
שזה גורר 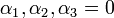 .
.
דוגמא 2
2. (דוגמא מייצגת) 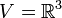 מעל
מעל 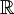 . האם הקבוצה
. האם הקבוצה
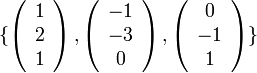 בת"ל?
בת"ל?
נתבונן ב
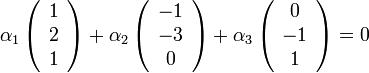 ונמיר אותו להצגה מטריצית
ונמיר אותו להצגה מטריצית
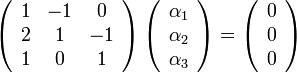
כעת השאלה שקולה האם יש פתרון לא טריאלי למערכת. נדרג ונבדוק
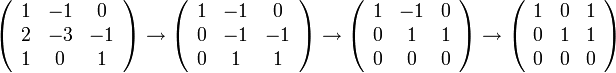
לכל הצבה  נקבל
נקבל
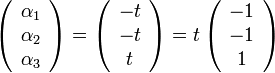 פתרון לא טרוויאלי. כלומר הוקטורים הנ"ל ת"ל.
פתרון לא טרוויאלי. כלומר הוקטורים הנ"ל ת"ל.
אם רוצים לראות את זה מפורש ניקח למשל 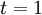 ונקבל צ"ל לא טריוואלי שמתאפס
ונקבל צ"ל לא טריוואלי שמתאפס
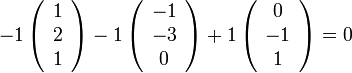
דוגמא 3
יהי 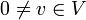 אזי
אזי 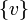 קבוצה בת"ל.
קבוצה בת"ל.
לחילופין יהי 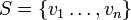 כך ש
כך ש 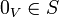 אזי
אזי  ת"ל (ניקח צ"ל שכל המקדמים שווים אפס פרט למקדם של וקטור האפס שניקח להיות שווה 1).
ת"ל (ניקח צ"ל שכל המקדמים שווים אפס פרט למקדם של וקטור האפס שניקח להיות שווה 1).
דוגמא 4
![V=\mathbb{R}_{2}[x]](/images/math/f/7/3/f73cc35842c78e71bd2b26bb136b5c6a.png) מרחב הפלינומים עד דרגה 2 מעל
מרחב הפלינומים עד דרגה 2 מעל 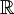 תהא
תהא 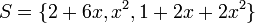 . האם
. האם  בת"ל?
בת"ל?
פתרון: צריך לבדוק האם 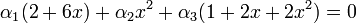 גורר שזה הצ"ל הטריאלי.
גורר שזה הצ"ל הטריאלי.
לפי השוואת מקדמים נקבל כי : 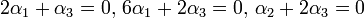
ובצורה מטריצית
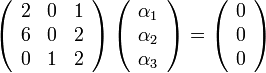
נבדוק אם למערכת יש פתרון לא טריאלי.
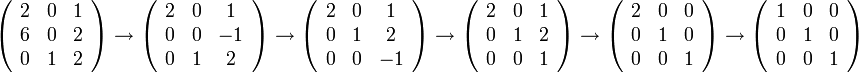
כלומר התשובה היא שלמערכת אין פתרון לא טריאלי. כלומר  בת"ל
בת"ל
דוגמא 5
תרגיל.
האם הפולינומים 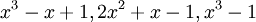 תלויים לינארית?
תלויים לינארית?
פתרון:
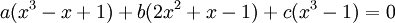 אם"ם
אם"ם
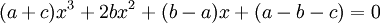 אם"ם
אם"ם
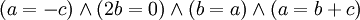 אם"ם
אם"ם
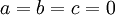
אם כן, הצירוף הלינארי היחיד שמתאפס הינו הטריוויאלי ולכן הפולינומים בת"ל.
דוגמא 6
הקבוצה ![\{1,x,x^2,x^3,\dots \}\subseteq \mathbb{F}[x]](/images/math/1/c/6/1c65551da35eaca80c68bb3035611b74.png) היא בת"ל
היא בת"ל
משפט
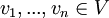 ת"ל אם"ם אחד מהוקטורים הינו צירוף לינארי של האחרים
ת"ל אם"ם אחד מהוקטורים הינו צירוף לינארי של האחרים
הוכחה
הוקטורים ת"ל אם"ם קיימים סקלרים כך ש 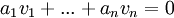 , ולפחות אחד מבין הסקלרים שונה מאפס. נניח ב.ה.כ. (בלי הגבלת הכלליות) ש
, ולפחות אחד מבין הסקלרים שונה מאפס. נניח ב.ה.כ. (בלי הגבלת הכלליות) ש 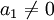 . לכן
. לכן 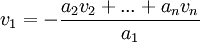 ולכן
ולכן 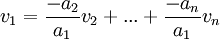 .
.
בכיוון הפוך נניח כי (ב.ה.ב) הוקטור הראשון 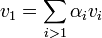 הוא צ"ל של האחרים. אזי
הוא צ"ל של האחרים. אזי 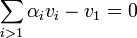 . כלומר קיבלנו צ"ל שמתאפס שיש מקדם אחד לפחות ששונה מאפס (המקדם של
. כלומר קיבלנו צ"ל שמתאפס שיש מקדם אחד לפחות ששונה מאפס (המקדם של 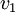 הוא
הוא 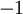 ) על פי הגדרה הוקטורים ת"ל
) על פי הגדרה הוקטורים ת"ל
שימו לב שיצא לנו שהוקטור הראשון תמיד צ"ל של האחרים, כמובן שזה לא נכון. זה נובע רק מטיעון ב.ה.כ שלנו, קל למצוא דוגמאות בהן הוקטור הראשון אינו צ"ל של האחרים.
ממשפט זה קל לנו לראות שהצלחנו בהגדרה שלנו לתלות:
מסקנה: אם 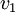 הינו צירוף לינארי של האחרים ניתן להסיר אותו במובן הבא:
הינו צירוף לינארי של האחרים ניתן להסיר אותו במובן הבא: 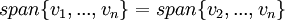 .
.
תרגיל
תרגיל: במרחב ![V=\mathbb{R}_{2}[x]](/images/math/f/7/3/f73cc35842c78e71bd2b26bb136b5c6a.png) נגדיר
נגדיר 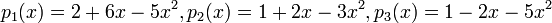 האם
האם 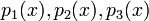 בת"ל? אם לא, מצאו צי"ל לא טריוואלי שמתאפס.
בת"ל? אם לא, מצאו צי"ל לא טריוואלי שמתאפס.
תרגיל
תרגיל: יהא  מ"ו ויהיו
מ"ו ויהיו 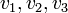 וקטורים. הוכיחו/הפריכו: אם
וקטורים. הוכיחו/הפריכו: אם 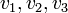 בת"ל בזוגות (כלומר כל זוג וקטורים שונים בת"ל) אזי
בת"ל בזוגות (כלומר כל זוג וקטורים שונים בת"ל) אזי
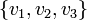 בת"ל.
בת"ל.
תרגיל
תרגיל: יהא V מ"ו ויהיו 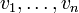 וקטורים. אם
וקטורים. אם 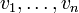 בת"ל אזי הוקטורים
בת"ל אזי הוקטורים 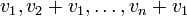 גם בת"ל.
גם בת"ל.
תרגיל
יהא 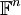 מ"ו ו
מ"ו ו 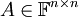 מטריצה ריבועית. הוכיחו: (
מטריצה ריבועית. הוכיחו: ( הפיכה)
אמ"מ (לכל
הפיכה)
אמ"מ (לכל 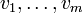 בת"ל מתקיים כי
בת"ל מתקיים כי 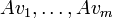 בת"ל.)
בת"ל.)
תרגיל
תרגיל: יהא 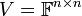 ותהא
ותהא 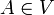 הפיכה. הוכיחו/הפריכו:
הפיכה. הוכיחו/הפריכו: 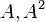 בת"ל.
בת"ל.
ושוב, בחזרה למערכות משוואות לינאריות
תרגיל - הקשר בין צירוף לינארי לבין פתרון מערכת משוואות לינאריות=
יהיו 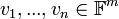 נגדיר
נגדיר 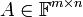 להיות המטריצה שעמודותיה הן
להיות המטריצה שעמודותיה הן 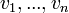 (כלומר
(כלומר 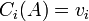 ).
).
יהיה 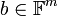 וקטור (פתרון).
וקטור (פתרון).
הוכח כי:
1. 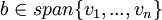 אם"ם קיים פתרון למערכת
אם"ם קיים פתרון למערכת 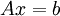
2. במקרה זה הפתרון 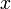 הינו וקטור הסקלרים של הצירוף הלינארי שנותן את b.
כלומר, כאשר
הינו וקטור הסקלרים של הצירוף הלינארי שנותן את b.
כלומר, כאשר 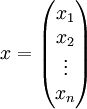 מתקיים
מתקיים 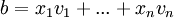
3.נניח והוקטורים שייכים למרחב 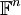 (כלומר
(כלומר 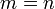 והמטריצה ריבועית). הוכח שקיים צירוף לינארי יחיד הנותן את
והמטריצה ריבועית). הוכח שקיים צירוף לינארי יחיד הנותן את 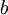 אם"ם המטריצה הינה הפיכה. מה ניתן להסיק על הוקטורים במקרה זה?
אם"ם המטריצה הינה הפיכה. מה ניתן להסיק על הוקטורים במקרה זה?
פתרון
1+2. ישירות מכפל עמודה-עמודה נקבל כי 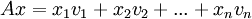 . לפיכך, ברור שקיים פתרון למערכת Ax=b אם"ם קיימים סקלרים כך ש
. לפיכך, ברור שקיים פתרון למערכת Ax=b אם"ם קיימים סקלרים כך ש 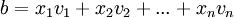 .
.
אמנם התרגיל הזה טריוויאלי למדי אך חשוב מאד לזכור תוצאה זו, היא תשמש אותנו בהמשך רבות. בניסוח קליט: 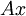 הינה צירוף לינארי של עמודות
הינה צירוף לינארי של עמודות  עם הסקלרים מ-
עם הסקלרים מ-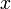 .
.
3. אם המטריצה הפיכה אזי 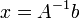 הוא הפתרון היחיד. ולהפיך אם קיים צירוף לינארי יחיד הנותן את
הוא הפתרון היחיד. ולהפיך אם קיים צירוף לינארי יחיד הנותן את 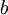 אזי אם נדרג את
אזי אם נדרג את  קנונית נגיע למטריצת היחידה. זה אומר ש
קנונית נגיע למטריצת היחידה. זה אומר ש  הפיכה.
הפיכה.
במקרה זה שהמטריצה הפיכה נסיק כי גם למערכת 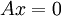 יש פתרון יחיד שהוא
יש פתרון יחיד שהוא 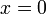 . כלומר צ"ל היחיד של עמודות
. כלומר צ"ל היחיד של עמודות  שמתאפס הוא הצ"ל הטריוויאלי. כלומר עמודות
שמתאפס הוא הצ"ל הטריוויאלי. כלומר עמודות  בת"ל.
בת"ל.
בנוסף, מכיוון שאנו יודעים שמטריצה הפיכה אם"ם המשולחפת שלה הפיכה, ניתן גם להסיק שמטריצה הינה הפיכה אם"ם שורותיה בת"ל.
בסיס ומימד
הגדרה: יהיה  מרחב וקטורי (או תת מרחב) מעל
מרחב וקטורי (או תת מרחב) מעל  . קבוצה
. קבוצה 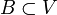 תקרא בסיס אם
תקרא בסיס אם
-
 בת"ל
בת"ל -
 פורשת את המרחב, כלומר
פורשת את המרחב, כלומר 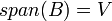
הגדרה: המימד של  הוא
הוא 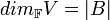 (מספר האיברים ב
(מספר האיברים ב  ) כאשר
) כאשר  הוא בסיס.
אם
הוא בסיס.
אם 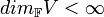 אזי
אזי  יקרא נוצר סופית.
יקרא נוצר סופית.
משפט: ההגדרה של מימד מוגדרת היטב ואינה תלויה בבחירת הבסיס. כלומר כל שתי בסיסים 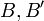 בעלי אותה עוצמה (בעלי אותו מספר איברים).
בעלי אותה עוצמה (בעלי אותו מספר איברים).
משפט: לכל מרחב וקטורי קיים בסיס
דוגמאות
בסיסים סטנדרטים:
1.
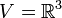 אזי
אזי
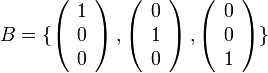 הוא בסיס. (המימד 3)
הוא בסיס. (המימד 3)
בהכללה
הבסיס הסטנדרטי ל 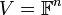 הוא
הוא 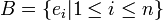 ("וקטורי היחידה")
("וקטורי היחידה")
2.
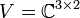 אזי
אזי
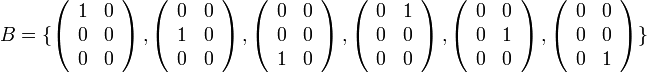 הוא בסיס. (המימד הוא
הוא בסיס. (המימד הוא 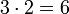 )
)
בהכללה: הבסיס הסטנדרטי ל 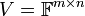 הוא
הוא 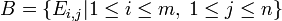 ("מטריצות היחידה")
("מטריצות היחידה")
3.
![V=\mathbb{R}_{2}[x]](/images/math/f/7/3/f73cc35842c78e71bd2b26bb136b5c6a.png) מרחב הפלינומים מדרגה 2 מעל. בסיס
מרחב הפלינומים מדרגה 2 מעל. בסיס 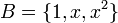 (מימד 2+1)
(מימד 2+1)
בהכללה הבסיס הסטנדרטי ל ![V=\mathbb{F}_{n}[x]](/images/math/8/0/b/80b596b0b4b56dd69cfee9bf4296613e.png) הוא
הוא 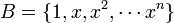
4.
מרחב הפולינומים ![\mathbb{F}[x]](/images/math/8/a/a/8aa38b82569f040ccef12e0c6ae18eca.png) . הבסיס
. הבסיס 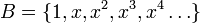 הוא בסיס אינסופי.
הוא בסיס אינסופי.
5. לפי הגדרה, הבסיס למרחב האפס  הוא הקבוצה הריקה
הוא הקבוצה הריקה 
הערה: 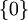 אינו בסיס כי כל קבוצה המכילה את 0 היא תלויה לינארית
אינו בסיס כי כל קבוצה המכילה את 0 היא תלויה לינארית
תכונה חשובה של בסיס
תרגיל: יהא  מרחב וקטורי,
מרחב וקטורי, 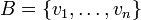 בסיס.
בסיס.
אזי כל 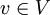 ניתן להציג כצ"ל של
ניתן להציג כצ"ל של  בצורה יחידה.
בצורה יחידה.
הוכחה
יהי 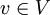
- כיוון ש
 פורשת את
פורשת את  קיים צ"ל של
קיים צ"ל של  ששווה ל
ששווה ל 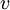
- יחידות: נניח שני צ"ל של
 שווים ל
שווים ל 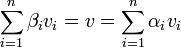 נוכיח כי זהו אותו צ"ל (כלומר המקדמים שווים). אכן אם נעביר אגף נקבל כי
נוכיח כי זהו אותו צ"ל (כלומר המקדמים שווים). אכן אם נעביר אגף נקבל כי 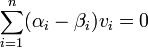 . כיוון ש
. כיוון ש  בת"ל נקבל כי
בת"ל נקבל כי 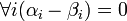 ולכן
ולכן 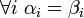 כנדרש.
כנדרש.
הגדרה יהא  מרחב וקטורי,
מרחב וקטורי, 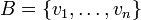 בסיס ויהי
בסיס ויהי 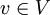 . ההצגה של
. ההצגה של 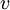 לפי בסיס
לפי בסיס  הוא וקטור המקדמים בצ"ל. כלומר
הוא וקטור המקדמים בצ"ל. כלומר
![[v]_B=
\left(\begin{array}{c}
\alpha_{1}\\
\alpha_{2}\\
\vdots\\
\alpha_{n}
\end{array}\right)\in\mathbb{F}^{n}](/images/math/7/4/d/74d094b5c206d8f2ceae7d7071d3f6b5.png) אמ"מ
אמ"מ
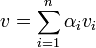
לפני שנעבור לדוגמאות יותר מסובכות נראה קריטריונים שקולים לבסיס
קריטריונים שקולים לבסיס
בהגדרה של תלות לינארית ראינו שאפשר לראות תלות לינארית בתור היכולת לזרוק וקטורים מבלי להשפיע על המרחב הנפרש.
הטענה הנ"ל באופן פורמאלי היא הטענה הבאה:
טענה: יהיה  מרחב וקטורי מעל
מרחב וקטורי מעל  . תהא
. תהא 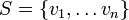 קבוצה ונניח כי קיים
קבוצה ונניח כי קיים 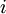 כך ש
כך ש 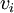 תלוי באחרים.
תלוי באחרים.
אזי 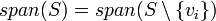
כמובן שלפעולה זו יש סוף - מתישהו לא ניתן לזרוק אף וקטור מבלי לגרוע מהמרחב הנפרש. הקבוצה שנשארנו איתה תהיה בסיס.
זוהי בניה "מלמעלה ללמטה". כלומר מתחילים עם  ו"זורקים" וקטורים כמה שניתן.
ו"זורקים" וקטורים כמה שניתן.
בניה נוספת היא בניה "מלמטה ללמעלה". מתחילים עם הקבוצה הריקה ומוסיפים וקטורים כך שהקבוצה המתקבלת היא בת"ל. כמובן שגם לפעולה זאת יש סוף (אחרי מספר צעדים השווה למימד של המרחב) - מתי שלא ניתן להוסיף אף וקטור מבלי לגרוע מ"בת"ליות" הקבוצה, הגענו לבסיס.
בניה זאת מתבססת על הטענה הבאה:
טענה:
יהיה  מרחב וקטורי מעל
מרחב וקטורי מעל  ותהא
ותהא 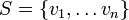 קבוצה בת"ל.
קבוצה בת"ל.
אם קיים 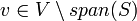 אז
אז 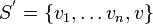 בת"ל גם כן.
בת"ל גם כן.
הוכחה: נניח 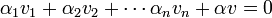
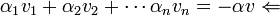
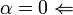 כי אחרת נקבל ש
כי אחרת נקבל ש 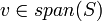 ע"י חילוק ב
ע"י חילוק ב 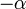
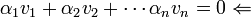
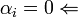 כי
כי  בת"ל.
בת"ל.
לסיכום:
משפט:
יהיה 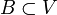 אזי התנאים הבאים שקולים:
אזי התנאים הבאים שקולים:
-
 בסיס.
בסיס. -
 קבוצה בת"ל מקסימאלית
קבוצה בת"ל מקסימאלית -
 קבוצה פורשת את
קבוצה פורשת את  - מינימאלית.
- מינימאלית.
מסקנה חשובה ממפרק זה היא
- כל קבוצה
 בת"ל ניתן להשלים לבסיס
בת"ל ניתן להשלים לבסיס - לכל קבוצה פורשת
 קיימת תת קבוצה שהיא בסיס
קיימת תת קבוצה שהיא בסיס
(חידה מטופשת: אם ניקח את המימד של צירוף לינארי נקבל מנה טעימה. מהי?)
תרגיל
מצא בסיס למרחב הפתרונות של המערכת
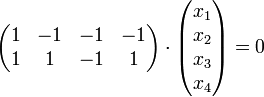
פתרון: נדרג
עיבוד הנוסחה נכשל (שגיאת תחביר): \begin{pmatrix} 1 &-1 &-1 & -1\\ 1 &1 &-1 &1 \end{pmatrix} \to \begin{pmatrix} 1 &-1 &-1 & -1\\ 0 &2 & 0 & 2\\ \end{pmatrix} \to \\ \begin{pmatrix} 1 &-1 &-1 & -1\\ 0 &1 & 0 & 1\\ \end{pmatrix} \to \begin{pmatrix} 1 &0 &-1 &0\\ 0 &1 & 0 & 1\\ \end{pmatrix}
ולכן הפתרונות הן
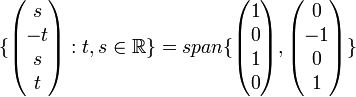
אלו נקראים הפתרונות היסודיים והם מהווים בסיס למרחב הפתרונות
תרגיל
מצא בסיס לתת המרחב
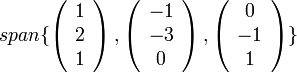 של
של
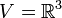
פתרון:
כיוון שיש לנו כבר קבוצה פורשת, נותר רק ל"זרוק" את הוקטורים התלויים לינארית. נעשה זאת ע"י ע"י דירוג מטריצה
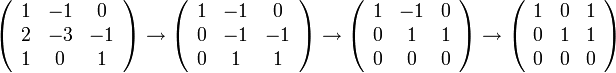
כלומר הוקטור השלישי תלוי לינארית בשניים הראשונים ולכן
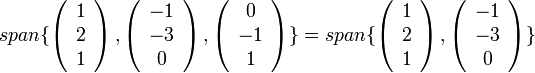
וזהו בסיס כי הוקטורים האלה כבר בת"ל
משפט השלישי חינם
יהיה  מ"ו ותהי
מ"ו ותהי  תת קבוצה.
אם שניים מבין התנאים הבאים מתקיימים, השלישי מתקיים בהכרח (בחינם) ומתקיים ש
תת קבוצה.
אם שניים מבין התנאים הבאים מתקיימים, השלישי מתקיים בהכרח (בחינם) ומתקיים ש  היא בסיס ל
היא בסיס ל  :
:
-
 בת"ל
בת"ל 
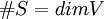 (מספר האיברים ב
(מספר האיברים ב שווה למימד של
שווה למימד של  .
.
תרגיל
תרגיל: 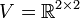 . השלם את
. השלם את
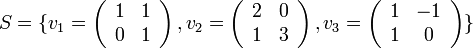 לבסיס
לבסיס
פתרון:
ראינו כבר כי
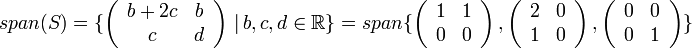
מכאן אפשר לראות בקלות כי
-
 בת"ל. כי
בת"ל. כי  פורשת את
פורשת את 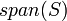 והמימד שלו 3 כמו גודל
והמימד שלו 3 כמו גודל  . על פי השלישי חינם
. על פי השלישי חינם  בת"ל.
בת"ל. -
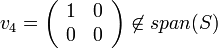 ולכן
ולכן 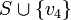 בת"ל גם כן (כמו שהוכחנו באחד התרגילים).
בת"ל גם כן (כמו שהוכחנו באחד התרגילים).
כעת קיבלנו ש 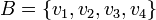 קבוצה בת"ל בת 4 איברים =
קבוצה בת"ל בת 4 איברים = 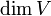 על פי השלישי חינם
על פי השלישי חינם  בסיס
בסיס
תרגיל חשוב
יהיה  מרחב וקטורי מעל
מרחב וקטורי מעל  . יהיה
. יהיה 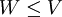 תת מרחב מאותו מימד סופי(נסמן
תת מרחב מאותו מימד סופי(נסמן 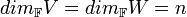 ).
).
הוכח: 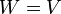
פתרון:
נבחר 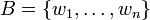 בסיס ל
בסיס ל 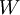 . בפרט מתקיים כי
. בפרט מתקיים כי
-
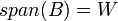
-
 בת"ל.
בת"ל.
עפי השלישי חינם, כיוון ש  בת"ל +
בת"ל + 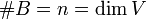 מתקיים כי
מתקיים כי 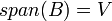 . ומכאן ש
. ומכאן ש 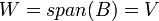
במילים: תת מרחב שמוכל בתת מרחב אחר מאותו מימד אז הם שווים
תרגיל חשוב (חלק מ7.7), הוכחה נוספת
נתון ש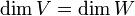 . נניח בשלילה ש
. נניח בשלילה ש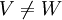 ונראה שנקבל סתירה . מכיוון שנתון
ונראה שנקבל סתירה . מכיוון שנתון 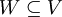 העובדה ש
העובדה ש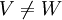 גוררת בהכרח שקיים וקטור
גוררת בהכרח שקיים וקטור 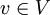 כך ש
כך ש 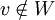 (זה תרגיל לוגי פשוט). נסמן dimW=dimV=n וניקח בסיס כלשהו לW (אנחנו יודעים שקיים כזה)
(זה תרגיל לוגי פשוט). נסמן dimW=dimV=n וניקח בסיס כלשהו לW (אנחנו יודעים שקיים כזה) 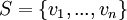 .
.
כעת, נוכיח ש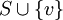 בהכרח בת"ל. נניח בשלילה שהיא כן תלוייה, לכן יש צירוף לינארי לא טריוויאלי של
בהכרח בת"ל. נניח בשלילה שהיא כן תלוייה, לכן יש צירוף לינארי לא טריוויאלי של 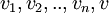 שמתאפס. נניח והמקדם של v שונה מאפס, לכן קל להראות שהוא צירוף לינארי של האחרים בסתירה לכך ש-v אינו שייך לW (הרי יש סגירות בW לצירופים לינאריים) לכן המקדם של v הינו אפס. כעת נשארנו עם צירוף לינארי לא טריוויאלי שמתאפס של
שמתאפס. נניח והמקדם של v שונה מאפס, לכן קל להראות שהוא צירוף לינארי של האחרים בסתירה לכך ש-v אינו שייך לW (הרי יש סגירות בW לצירופים לינאריים) לכן המקדם של v הינו אפס. כעת נשארנו עם צירוף לינארי לא טריוויאלי שמתאפס של 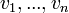 וזו סתירה לכך שהם בת"ל מתוקף הגדרתם כבסיס.
וזו סתירה לכך שהם בת"ל מתוקף הגדרתם כבסיס.
על כן, מצאנו קבוצה בת"ל המכילה n+1 וקטורים, בסתירה לכך שהמימד של W הוא n.
התוצאה של תרגיל זה, כאמור, חשובה מאד. אם W תת מרחב של V והוכחנו שהם מאותו המימד זה מספיק על מנת להגיד שהם שווים. אתם תדרשו בעצם לעשות הוכחות כאלה באמצעות מימדים לא פעם ואף לא פעמיים.
תרגיל
יהא ![V= \mathbb{R}_2[x]](/images/math/4/9/5/495528b4842c3efec23cbf769dd776da.png) . מצא בסיס לחיתוך ובסיס לסכום.
. מצא בסיס לחיתוך ובסיס לסכום.
בין 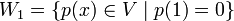
לבין 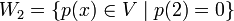
פתרון
א. בסיס לחיתוך: החיתוך הוא פשוט 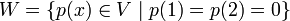 .
.
מתקיים כי 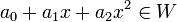 אמ"מ
אמ"מ 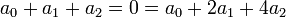 .
.
רואים שזהו מערכת משוואות עם משתנה חופשי אחד (המערכת היא 2 משוואות עם 3 נעלמים) ולכן המימד של W הוא 1.
לפי משפט השלישי חינם מספיק למצוא 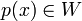 ואז הוא יהווה בסיס. הנה דוגמא
ואז הוא יהווה בסיס. הנה דוגמא 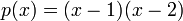 .
.
ב. בסיס לסכום: ראשית נציג אותם כנפרשים, ע"י מציאת הפתרונות למשוואות בהגדרת תתי-המרחבים: 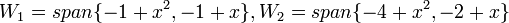 . לכן נקבל:
. לכן נקבל: 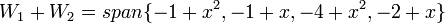 , ואז נמצא את הבסיס ע"י למצוא מבין אלה וקטורים שהצ"ל נותן 0 אמ"ם הטריוויאלי, ונקבל ששלושת הראשונים עושים זאת. קיבלנו
, ואז נמצא את הבסיס ע"י למצוא מבין אלה וקטורים שהצ"ל נותן 0 אמ"ם הטריוויאלי, ונקבל ששלושת הראשונים עושים זאת. קיבלנו![\dim(W_1+W_2)=3=\dim(\mathbb{R}_2[x])](/images/math/7/2/5/72595fe3e98a4637a204d58d1c599773.png) , ולכן
, ולכן ![W_1+W_2=\mathbb{R}_2[x]](/images/math/e/d/d/edd19d3c01c7e2a981880b1e65ce61fe.png) .
.
תרגיל
תרגיל: במרחב 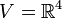 , מצאו בסיס ל
, מצאו בסיס ל 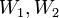 ולסכום ולחיתוך שלהם כאשר
ולסכום ולחיתוך שלהם כאשר
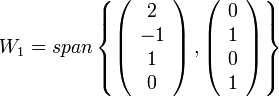
ו 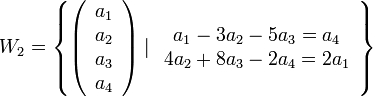
תרגיל
.2 תרגיל: במרחב ![V=\mathbb{R}_{3}[x]](/images/math/9/8/9/989d9ff01be4a27f1feb5d2881f8d85b.png) , מצאו בסיס ל
, מצאו בסיס ל 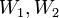 ולסכום ולחיתוך שלהם כאשר
ולסכום ולחיתוך שלהם כאשר
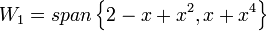 ו
ו 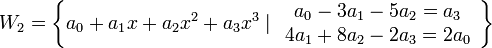
תרגיל
הוכיחו לכל מטריצה 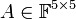 מתקיים שהמטריצות
מתקיים שהמטריצות 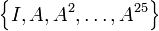 ת"ל במרחב
ת"ל במרחב 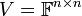 .
.
האם קיימת מטריצה 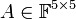 כך ש
כך ש 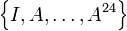 בת"ל?? (שאלה קשה!)
בת"ל?? (שאלה קשה!)
תרגיל
יהא  מ"ו. יהיו
מ"ו. יהיו 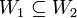 תתי מרחבים. הוכיחו/הפירכו: כל בסיס של
תתי מרחבים. הוכיחו/הפירכו: כל בסיס של 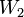 ניתן לצמצום לבסיס של
ניתן לצמצום לבסיס של 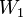 .
.
תרגיל 7.17
יהא V מ"ו, ותהא B קבוצה המוכלת בV. הוכח שהתנאים הבאים שקולים:
(1)  בסיס עבור
בסיס עבור 
(2) וקטור האפס אינו שייך לB ולכל קבוצה 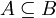 מתקיים
מתקיים 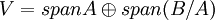
הוכחה
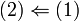
נניח B בסיס לV, ברור מכך שB בת"ל שהוא אינו מכיל את אפס. תהי A קבוצה המוכלת בB נסמן ב.ה.כ 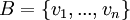 ו
ו 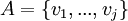 . יש להוכיח בעצם שמתקיים
. יש להוכיח בעצם שמתקיים 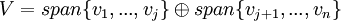 . לצורך זה יש להוכיח שני דברים:
. לצורך זה יש להוכיח שני דברים:
(שימו לב שאם A ריקה, המשפט נובע בקלות ולכן לא נתייחס עוד למקרה קצה זה.)
התנאי הראשון: יהא 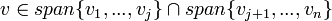 צ"ל
צ"ל 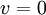 . מהגדרת החיתוך נובע כי קיימים סקלרים כך ש
. מהגדרת החיתוך נובע כי קיימים סקלרים כך ש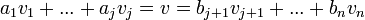 . נעביר אגף ונקבל כי
. נעביר אגף ונקבל כי 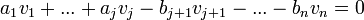 כיוון ש
כיוון ש  בת"ל נובע כי כל המקדמים שווים 0 ובפרט
בת"ל נובע כי כל המקדמים שווים 0 ובפרט 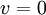 כנדרש.
כנדרש.
התנאי השני: 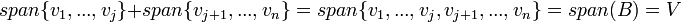
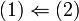
מכיוון שזה נכון לכל קבוצה A המוכלת בB, בפרט זה נכון לקבוצה הריקה. לכן יוצא ש 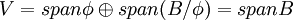 כלומר B פורש את V. נותר להראות שB בת"ל.
כלומר B פורש את V. נותר להראות שB בת"ל.
נניח בשלילה שB אינה בת"ל, לכן וקטור אחד ממנה u הוא צירוף לינארי של האחרים. נסמן בA את הנקודון שמכיל את u כלומר 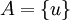 ומכייון שבהכרח
ומכייון שבהכרח 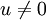 נקבל סתירה לתכונת הסכום הישר (חיתוך שכולל רק את ווקטור האפס)
נקבל סתירה לתכונת הסכום הישר (חיתוך שכולל רק את ווקטור האפס)