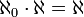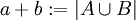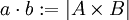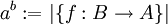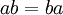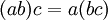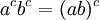הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 7"
אחיה בר-און (שיחה | תרומות) (←תרגיל) |
אחיה בר-און (שיחה | תרומות) (←תרגיל (ממבחן)) |
||
| (46 גרסאות ביניים של 6 משתמשים אינן מוצגות) | |||
| שורה 2: | שורה 2: | ||
==אריתמטיקה של עוצמות== | ==אריתמטיקה של עוצמות== | ||
| + | |||
'''הגדרה''' יהיו A,B קבוצות אזי <math>A^B:=\{f:B\rightarrow A\}</math>. | '''הגדרה''' יהיו A,B קבוצות אזי <math>A^B:=\{f:B\rightarrow A\}</math>. | ||
| + | |||
| + | ===תרגיל=== | ||
| + | יהיו A,B,C קבוצות כך ש <math>|A|\leq |B|</math>. הוכיחו כי <math>|A^C|\leq|B^C|</math>. | ||
| + | |||
| + | פתרון: נתון שקיימת <math>f:A\to B</math> חח"ע. נגדיר <math>g:A^C\to B^C</math> ע"י <math>h:C\to A\mapsto f\circ h</math>. מתקיים כי g חח"ע כי f חח"ע ויש לה הפיכה שמאלית. | ||
| + | |||
| + | הערה: <math>|A|< |B|</math> '''לא''' גורר <math>|A^C|<|B^C|</math>. | ||
| + | |||
| + | |||
| + | |||
| + | ===תרגיל=== | ||
| + | הוכח שעוצמת קבוצת החזקה של A תמיד גדולה מעוצמתה של A | ||
| + | |||
| + | '''הוכחה.''' | ||
| + | יש התאמה חח"ע ועל <math>g:P(A)\to \{0,1\}^A</math> ע"י | ||
| + | <math>\forall B\subseteq A : g(B)=f_B=\chi_B</math> | ||
| + | |||
| + | לפי תרגיל קודם <math>|A|<|\{0,1\}^A|=|P(A)|</math> | ||
| + | |||
| + | '''הערה: (למי שלמד תורת הקבוצות)''' מסיבה זו אוסף העוצמות אינו קבוצה אלא מחלקה. שכן אם הוא היה קבוצה, הייתה לו עוצמה | ||
===תרגיל=== | ===תרגיל=== | ||
| שורה 20: | שורה 41: | ||
לפי הבנייה <math>\forall a\in A f\not=f_a</math> כיוון ש <math>f(a)\not=f_a(a)</math>. סתירה לכך ש g על. | לפי הבנייה <math>\forall a\in A f\not=f_a</math> כיוון ש <math>f(a)\not=f_a(a)</math>. סתירה לכך ש g על. | ||
| − | + | הערה: התרגיל הזה הוא מסקנה מהתרגילים הקודמים כי <math>|\{0,1\}|\leq |B|</math> ולכן <math>|A|<|\{0,1\}^A|\leq |B^A|</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
'''הגדרה:''' | '''הגדרה:''' | ||
| שורה 48: | שורה 59: | ||
**<math>a^0=1</math> שכן יש פונקציה יחידה מהקבוצה הריקה לכל מקום - היחס שהוא הקבוצה הריקה. | **<math>a^0=1</math> שכן יש פונקציה יחידה מהקבוצה הריקה לכל מקום - היחס שהוא הקבוצה הריקה. | ||
**<math>0^0=1</math> זה מקרה פרטי של הסעיף הקודם, ועדיין מתקיים | **<math>0^0=1</math> זה מקרה פרטי של הסעיף הקודם, ועדיין מתקיים | ||
| + | **<math>1^a=1</math> | ||
**<math>a\neq 0 \rightarrow 0^a=0</math> אין אף פונקציה מקבוצה לא ריקה אל קבוצה ריקה, שכן יחס כזה לא יכול להיות שלם. | **<math>a\neq 0 \rightarrow 0^a=0</math> אין אף פונקציה מקבוצה לא ריקה אל קבוצה ריקה, שכן יחס כזה לא יכול להיות שלם. | ||
| − | |||
===תכונות האריתמטיקה=== | ===תכונות האריתמטיקה=== | ||
| שורה 63: | שורה 74: | ||
נוכיח למשל <math>a^ba^c=a^{b+c}</math> יהיו <math>|A|=a,|B|=b,|C|=c</math> קבוצות זרות | נוכיח למשל <math>a^ba^c=a^{b+c}</math> יהיו <math>|A|=a,|B|=b,|C|=c</math> קבוצות זרות | ||
נגדיר פונקציה מ <math>A^{B\cup C} \to A^B\times A^C</math> ע"י <math>f \mapsto (f|_B,f|_C)</math>. היא חח"ע ועל. | נגדיר פונקציה מ <math>A^{B\cup C} \to A^B\times A^C</math> ע"י <math>f \mapsto (f|_B,f|_C)</math>. היא חח"ע ועל. | ||
| + | |||
| + | נוכיח למשל <math>(a^b)^c=a^{bc}</math> יהיו <math>|A|=a,|B|=b,|C|=c</math> קבוצות זרות | ||
| + | נגדיר פונקציה מ <math>(A^B)^C \to A^{B\times C} </math> ע"י <math>f \mapsto g(b,c)= f(c)(b)</math>. היא חח"ע ועל. | ||
| שורה 90: | שורה 104: | ||
דרך ב- אריתמטיקה- | דרך ב- אריתמטיקה- | ||
| − | <math>\aleph \ | + | <math>\aleph \cdot \aleph=2^{\aleph_0}\cdot 2^{\aleph_0}=2^{\aleph_0+\aleph_0}=2^{\aleph_0}=\aleph </math> |
| − | דרך ג- מהנוסחא- <math>\aleph \ | + | דרך ג- מהנוסחא- <math>\aleph \cdot \aleph=max\{\aleph,\aleph\}=\aleph </math> |
===תרגיל=== | ===תרגיל=== | ||
| שורה 101: | שורה 115: | ||
כיוון ש <math>\mathbb{R}\backslash \mathbb{Q}</math> מוכל בממשיים עוצמתה לכל היותר אלף. נניח בשלילה כי עוצמתה שווה a קטנה ממש מאלף אזי | כיוון ש <math>\mathbb{R}\backslash \mathbb{Q}</math> מוכל בממשיים עוצמתה לכל היותר אלף. נניח בשלילה כי עוצמתה שווה a קטנה ממש מאלף אזי | ||
| − | <math>\aleph=|\mathbb{R}|=|\mathbb{R}\backslash \mathbb{Q}|+|\mathbb{Q}|=a+\ | + | <math>\aleph=|\mathbb{R}|=|\mathbb{R}\backslash \mathbb{Q}|+|\mathbb{Q}|=a+\aleph_0=a<\aleph</math>. סתירה |
| + | === תרגיל === | ||
| + | חשבו את <math>\aleph^{\aleph_0},{\aleph_0}^{\aleph}</math> | ||
| + | |||
| + | פתרון: <math>\aleph^{\aleph_0}=\aleph,{\aleph_0}^{\aleph}=2^{\aleph}</math> | ||
| + | |||
| + | הסיקו כי עוצמת קבוצת הפונקציות מהרציונאלים לממשיים היא <math>\aleph</math>. | ||
===תרגיל=== | ===תרגיל=== | ||
| − | תהא <math>A</math> קבוצה אינסופית. | + | תהא <math>A</math> קבוצה אינסופית ו <math>B\subseteq A</math> תת קבוצה. |
הוכח/הפרך | הוכח/הפרך | ||
| − | |||
1. <math>|A\backslash B|=|A|\Rightarrow |B|<|A|</math> | 1. <math>|A\backslash B|=|A|\Rightarrow |B|<|A|</math> | ||
| + | |||
| + | 2. <math>|A\backslash B|=|A|\Leftarrow |B|<|A|</math> | ||
פתרון: | פתרון: | ||
| − | 1. | + | 1. הפרכה: ניקח את השלמים והטבעיים |
| − | + | ||
| − | 2. | + | 2. נכון כי ניתן להציג A כאיחוד זר <math>A=A\backslash B \cup B</math> |
| + | ולכן <math>|A|=|A\backslash B| + |B|</math>. אם <math>|A\backslash B|<|A|</math> נקבל סתירה | ||
| + | |||
| + | === תרגיל === | ||
| + | 1. מה עוצמת <math>\mathbb{N}^\mathbb{N}</math> | ||
| + | |||
| + | פתרון: <math>\aleph_0^{\aleph_0} =2^{\aleph_0} </math> | ||
| + | |||
| + | 2. מה עוצמת <math>X=\{f\in \mathbb{N}^\mathbb{N}:f(1)\leq f(2)\}</math> | ||
| + | |||
| + | פתרון: לכל היותר <math>\mathbb{N}^\mathbb{N}</math> ולכל הפחות <math>\mathbb{N}^\mathbb{N}</math> | ||
| + | כי לכל <math>g\in \mathbb{N}^{\mathbb{N}\setminus \{1,2\}}</math> נתאים <math>f\in X</math> ע"י <math>f(1)=f(2)=1 </math> ועבור <math>x\neq 1,2</math> נגדיר <math>f(x)=g(x)</math> ולכן <math>|\mathbb{N}^{\mathbb{N}\setminus \{1,2\}}|\leq|X|\leq |\mathbb{N}^\mathbb{N}|</math> ולפי ק.ש.ב יש שיווון | ||
| + | |||
| + | 3. מה עוצמת <math>X=\{f\in \mathbb{R}^\mathbb{R}:\forall x\notin \mathbb{Q} f(x)=1\}</math> | ||
| + | |||
| + | פתרון: X שווה עוצמה ל <math>\mathbb{R}^{\mathbb{Q}}</math> כי <math>g\in\mathbb{R}^{\mathbb{Q}}</math> ממופה ל <math>f\in X</math> המוגדרת <math>f|_{\mathbb{Q}}=g,f|_{\mathbb{R}\setminus\mathbb{Q}}=1</math> | ||
| + | |||
| + | === תרגיל === | ||
| + | תהי <math>\{A_i\}_{i\in I}</math> משפחה של קבוצות הזרות זו לזו כך שעוצמת כל אחת מהן ב<math>a</math>. נגדיר <math>\sum_{i\in I} a = |\bigcup_{i\in I}A_i|</math>. | ||
| + | הוכח כי <math>\sum_{i\in I} a = |I|\cdot a</math> | ||
| + | |||
| + | פתרון: | ||
| + | |||
| + | תהא <math>A</math> קבוצה נוספת מעוצמה <math>a</math>. | ||
| + | לכל <math>i\in I</math> קיימת פונקציה חח"ע ועל | ||
| + | <math>f_i:A\rightarrow A_i</math>. | ||
| + | כעת נגדיר פונקציה <math>g:I\times A\rightarrow\bigcup_{i\in I}A_i</math> ע"י <math>g(k,x)=f_k(x)</math>. מכיוון שהקבוצות זרות ו<math>f_k</math> חח"ע ברור שg חח"ע. מכיוון ש<math>f_k</math> על גם g על ולכן קיבלנו את המבוקש. | ||
| + | |||
| + | === תרגיל === | ||
| + | נגדיר <math>F</math> להיות אוסף תתי הקבוצות הסופיות של הטבעיים <math>F=\{X\subseteq \mathbb{N}:|X|<\aleph_0\}</math>. מה עוצמתה? | ||
| + | |||
| + | פתרון: לכל <math>i\in \mathbb{N}</math> נגדיר <math>F_i=\{X\subseteq \mathbb{N}:|X|=i\}</math> (אוסף תתי הקבוצות מגודל <math>i</math>). אזי <math>|F_i|\leq \aleph_0^i=\aleph_0</math> | ||
| + | ואז <math>|F|=|\cup_{i\in \mathbb{N}}F_i|\leq \aleph_0\cdot \aleph_0 =\aleph_0</math> | ||
| + | |||
| + | === תרגיל (בש.ב.)=== | ||
| + | נגדיר <math>A</math> להיות אוסף תתי הקבוצות האינסופיות של הטבעיים. מה עוצמתה? | ||
| + | |||
| + | פתרון: מתקיים כי <math>P(\mathbb{N})=A\cup A^c</math> כאשר A היא תתי הקבוצות הסופיות מתרגיל קודם שעוצמת <math>\aleph_0</math> | ||
| + | ולכן <math>2^{\aleph_0}=\aleph_0+|A^c|=\max\{\aleph_0,|A^c|\}=|A^c|</math> | ||
| + | |||
| + | === תרגיל === | ||
| + | נגדיר <math>A=\{X\subseteq \mathbb{R}: |X|=\aleph_0 \}</math> ,מה עוצמתה? | ||
| + | |||
| + | פתרון: לכל הפחות <math>2^{\aleph_0}</math> כי תתי הקבוצות האינסופיות של הטבעיים מעוצמה זאת. בצד שני נגדיר <math>F:\mathbb{R}^{\mathbb{N}}\to P(\mathbb{R})</math> ע"י | ||
| + | <math>f\mapsto Im(f)</math> טענה: <math>A\subseteq Im(F)</math> הוכחה: תהא <math>X\in A</math> ומהגדרת A, נסיק כי X מעוצמה הטבעיים ולכן קיימת <math>f:\mathbb{N}\to X</math> חח"ע ועל ולכן <math>F(f)=Im(f)=X</math>. מסקנה מכך <math>|A|\leq |Im(F)|\leq |\mathbb{R}^{\mathbb{N}}|=\aleph^{\aleph_0}=\aleph</math>. לפי ק.ש.ב <math>|A|=2^{\aleph_0}=\aleph</math> | ||
| + | |||
| + | === תרגיל === | ||
| + | |||
| + | נגדיר <math>A=\{X\subseteq \mathbb{R}: |X|=\aleph \}</math> ,מה עוצמתה? | ||
| + | |||
| + | פתרון: לכל היותר <math>2^\aleph</math> מצד שני <math>F:P((0,1))\to A </math> המוגדרת <math>B\mapsto B\cup (1,2)</math> חח"ע ולפי ק.ש.ב. סימנו | ||
===תרגיל ממבחן תשסח מועד א (ד"ר שי סרוסי וד"ר אלי בגנו) === | ===תרגיל ממבחן תשסח מועד א (ד"ר שי סרוסי וד"ר אלי בגנו) === | ||
| שורה 141: | שורה 211: | ||
ולכן <math>2^{\aleph_0}=|P(\mathbb{N})|=2a=a</math>. | ולכן <math>2^{\aleph_0}=|P(\mathbb{N})|=2a=a</math>. | ||
| + | === תרגיל === | ||
| + | נגדיר <math>X=\left\{ 0,1\right\} ^{\mathbb{N}}</math> קבוצת כל הסדרות הבינאריות. נגדיר יחס <math>\sim</math> על <math>X</math> כך <math>f\sim g</math> אמ"מ הקבוצה<math>\left\{ n\in\mathbb{N}\mid f(n)\neq g(n)\right\}</math> סופית | ||
| + | |||
| + | הוכיחו כי <math>\sim</math> יח"ש | ||
| + | |||
| + | לכל <math>f\in X</math>, מצאו את העוצמה של <math>[f]</math>. | ||
| + | |||
| + | מצאו את העוצמה של קבוצת המנה. | ||
| + | |||
| + | === תרגיל === | ||
| + | תהא <math>X\subseteq P(\mathbb{N})</math>. | ||
| + | |||
| + | מצאו <math>X</math> המקיימת: כל <math>A,B\in X</math> שונות הן זרות (כלומר <math>A\cap B=\emptyset</math>). | ||
| + | |||
| + | ניח <math>X</math> מקיימת: כל <math>A,B\in X</math> שונות הן זרות. הוכיחו כי <math>X</math> בת מנייה. | ||
| + | |||
| + | תהא <math>C\subseteq\mathbb{N}</math>. נניח <math>X</math> מקיימת: החיתוך של <math>A,B\in X</math> שונות הוא <math>C</math> (כלומר <math>A\cap B=C</math>). הוכיחו כי <math>X</math> בת מנייה. | ||
| + | |||
| + | נניח <math>X</math> מקיימת: החיתוך של <math>A,B\in X</math> שונות הוא לכל היותר בן 10 איברים (כלומר <math>\left|A\cap B\right|\leq10</math> ). הוכיחו כי <math>X</math> בת מנייה.רמז: <math>\cup_{B\in I}X_{B}</math> כאשר <math>I=\left\{ B\subseteq\mathbb{N}\mid\left|B\right|=10\right\}</math> ו <math>X_{B}=\left\{ S\in X\mid B\subseteq S\right\}</math> | ||
===תרגיל ממבחן תשע מועד א (ד"ר שי סרוסי וד"ר אפי כהן)=== | ===תרגיל ממבחן תשע מועד א (ד"ר שי סרוסי וד"ר אפי כהן)=== | ||
| שורה 168: | שורה 257: | ||
מוגדרת: לפי ההגדרה של יחס השקילות אכן מתקיים <math>f-g\in \mathbb{Z}^{\mathbb{R}}</math> | מוגדרת: לפי ההגדרה של יחס השקילות אכן מתקיים <math>f-g\in \mathbb{Z}^{\mathbb{R}}</math> | ||
| + | נראה כי ל F קיימת הופכית. נגדיר <math>G: \mathbb{Z}^{\mathbb{R}} \to [f]</math>. ע"י <math>G(h):=f-h </math>. הפונקציה מוגדרת היטב כי <math>f-(f-h)\in \mathbb{Z}^{\mathbb{R}}</math> וקל לוודא שזוהי ההופכית | ||
| + | |||
חח"ע: נניח <math>F(g)=F(h)</math> לכן <math>\forall x\in\mathbb{R} f(x)-g(x)=f(x)-h(x)</math> ולכן h=g. | חח"ע: נניח <math>F(g)=F(h)</math> לכן <math>\forall x\in\mathbb{R} f(x)-g(x)=f(x)-h(x)</math> ולכן h=g. | ||
| שורה 180: | שורה 271: | ||
נגדיר F פונקציה השולחת את <math>f\in\mathbb{R}^\mathbb{R}</math> לפונקציה <math>F(f):=f-\lfloor f\rfloor\in [0,1)^\mathbb{R}</math>. נראה ש-F מוגדרת היטב (על קבוצת המנה)וההפעלה שלה על קבוצת המנה תהיה חח"ע ועל. | נגדיר F פונקציה השולחת את <math>f\in\mathbb{R}^\mathbb{R}</math> לפונקציה <math>F(f):=f-\lfloor f\rfloor\in [0,1)^\mathbb{R}</math>. נראה ש-F מוגדרת היטב (על קבוצת המנה)וההפעלה שלה על קבוצת המנה תהיה חח"ע ועל. | ||
| − | מוגדרות: יהיו שתי פונקציות באותה מחלקת שקילות g,f. אזי, <math>F(g)-F(f)=g-\lfloor g\rfloor -f + \lfloor f\rfloor</math>. מכיוון שזהו הפרש של שני מספרים אי שליליים קטנים מאחד, זה שווה למספר | + | מוגדרות: יהיו שתי פונקציות באותה מחלקת שקילות g,f. אזי, <math>F(g)-F(f)=g-\lfloor g\rfloor -f + \lfloor f\rfloor</math>. מכיוון שזהו הפרש של שני מספרים אי שליליים קטנים מאחד, זה שווה למספר שבערכו המוחלט קטן מאחד. מכיוון שההפרש בין f ל-g שלם, המספר הזה הוא שלם. המספר השלם האי שלילי היחיד שקטן מאחד הינו אפס |
כלומר <math>F(f)=F(g)</math>. לכן הפונקציה F מוגדרת היטב שכן היא שולחת נציגים שונים של מחלקת שקילות לאותו מקום. | כלומר <math>F(f)=F(g)</math>. לכן הפונקציה F מוגדרת היטב שכן היא שולחת נציגים שונים של מחלקת שקילות לאותו מקום. | ||
| שורה 227: | שורה 318: | ||
חח"ע: נניח <math>(X_1,...,X_n)=x\neq x'=(X'_1,...,X'_m)</math>. אזי קיים <math>X_i\not=X'_i</math>, לכן קיים יהיה <math>a\in X_i/X'_i</math> (או להיפך) ואז <math>i=f_x(a)\not= f_{x'}(a)</math> | חח"ע: נניח <math>(X_1,...,X_n)=x\neq x'=(X'_1,...,X'_m)</math>. אזי קיים <math>X_i\not=X'_i</math>, לכן קיים יהיה <math>a\in X_i/X'_i</math> (או להיפך) ואז <math>i=f_x(a)\not= f_{x'}(a)</math> | ||
כלומר <math>g(x)\not=g(x') </math> | כלומר <math>g(x)\not=g(x') </math> | ||
| + | |||
| + | דרך 2- נגדיר פונקציה <math>g:X\to P(A)^{\mathbb{N}}</math> ע"י <math>g((X_1,...,X_n))(i) = \begin{cases}X_i & \text{if } 1\leq i \leq n \\ \emptyset & \text{if } n<i \end{cases} </math> | ||
| + | |||
| + | קל לראות כי הפונקציה חח"ע ולכן <math> |X| \leq (2^{a})^{\aleph_0} = 2^{a\cdot \aleph_0} =2^a</math> | ||
| + | |||
| + | דרך 3- נציג את X כאיחוד זר <math>X=\cup_{1<n\in \mathbb {N}}Y_n</math> כאשר <math>Y_n</math> זה חלוקות סדורות של A עם n קבוצות. כעת לכל n קיימת פונקציה <math>g:Y_n \to P(A)^n</math> | ||
| + | המוגדרת <math>g((X_1,...,X_n))=X_1 \times \cdots \times X_n</math> קל לראות שהיא חח"ע ולכן <math>|Y_n|=|A|^n =|A|</math> ולכן <math>|X|\leq \sum_{1<n\in \mathbb {N}}|A|=|A|\cdot \aleph_0 =|A|</math> | ||
כעת, קל למצוא פונקציה חח"ע מקבוצת החזקה של A ל-X - נשלח כל תת קבוצה לזוג שמכיל אותה ואת המשלים שלה. | כעת, קל למצוא פונקציה חח"ע מקבוצת החזקה של A ל-X - נשלח כל תת קבוצה לזוג שמכיל אותה ואת המשלים שלה. | ||
גרסה אחרונה מ־17:46, 5 באוגוסט 2020
תוכן עניינים
- 1 אריתמטיקה של עוצמות
- 1.1 תרגיל
- 1.2 תרגיל
- 1.3 תרגיל
- 1.4 תכונות האריתמטיקה
- 1.5 תרגיל
- 1.6 תרגיל
- 1.7 תרגיל
- 1.8 תרגיל
- 1.9 תרגיל
- 1.10 תרגיל
- 1.11 תרגיל
- 1.12 תרגיל
- 1.13 תרגיל (בש.ב.)
- 1.14 תרגיל
- 1.15 תרגיל
- 1.16 תרגיל ממבחן תשסח מועד א (ד"ר שי סרוסי וד"ר אלי בגנו)
- 1.17 תרגיל
- 1.18 תרגיל
- 1.19 תרגיל ממבחן תשע מועד א (ד"ר שי סרוסי וד"ר אפי כהן)
- 1.20 תרגיל ממבחן תשע מועד ב (ד"ר שי סרוסי וד"ר אפי כהן)
אריתמטיקה של עוצמות
הגדרה יהיו A,B קבוצות אזי 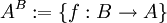 .
.
תרגיל
יהיו A,B,C קבוצות כך ש 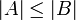 . הוכיחו כי
. הוכיחו כי 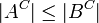 .
.
פתרון: נתון שקיימת 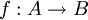 חח"ע. נגדיר
חח"ע. נגדיר 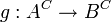 ע"י
ע"י 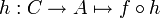 . מתקיים כי g חח"ע כי f חח"ע ויש לה הפיכה שמאלית.
. מתקיים כי g חח"ע כי f חח"ע ויש לה הפיכה שמאלית.
הערה: 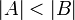 לא גורר
לא גורר 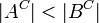 .
.
תרגיל
הוכח שעוצמת קבוצת החזקה של A תמיד גדולה מעוצמתה של A
הוכחה.
יש התאמה חח"ע ועל 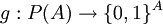 ע"י
ע"י
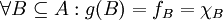
לפי תרגיל קודם 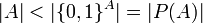
הערה: (למי שלמד תורת הקבוצות) מסיבה זו אוסף העוצמות אינו קבוצה אלא מחלקה. שכן אם הוא היה קבוצה, הייתה לו עוצמה
תרגיל
יהיו A,B קבוצות כך ש 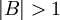 . הוכח כי
. הוכח כי 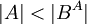 .
.
פתרון.
נבחר 2 איברים שונים 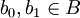 ונגדיר פונקציה חח"ע
ונגדיר פונקציה חח"ע 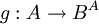 ע"י
ע"י 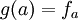 כאשר
כאשר 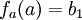 ו
ו 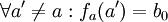 ולכן
ולכן 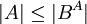 .
.
נניח בשלילה שקיים שיוויון אזי קיימת התאמה חח"ע ועל 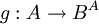 .
נסמן
.
נסמן 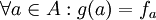 .
.
נראה באופן דומה לתירגול קודם כי g איננה על ע"י שנמצא פונקציה f שאין לה מקור:
נבחר 2 איברים שונים 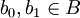 ונגדיר פונקציה באופן הבא
ונגדיר פונקציה באופן הבא 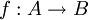 ע"י
ע"י
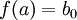 אם
אם 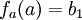 . ו-
. ו- 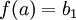 אחרת.
לפי הבנייה
אחרת.
לפי הבנייה 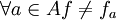 כיוון ש
כיוון ש 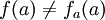 . סתירה לכך ש g על.
. סתירה לכך ש g על.
הערה: התרגיל הזה הוא מסקנה מהתרגילים הקודמים כי 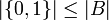 ולכן
ולכן 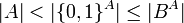
הגדרה:
יהיו שתי קבוצות זרות A,B כך ש 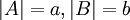 . אזי נגדיר פעולות בין עוצמות:
. אזי נגדיר פעולות בין עוצמות:
דוגמא: ראינו בתירגול קודם את הזיהוי 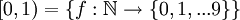 לכן
לכן 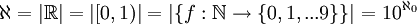
הערות:
- ההגדרות לעיל מוגדרות היטב, כלומר העוצמה נשארת זהה ללא תלות בבחירת הקבוצות המייצגות.
- בידקו שעבור המקרה הסופי מתקיים מה שמצופה.
למשל 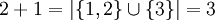
- שימו לב: מתוך הגדרה זו קל לראות את חוקי החזקות למקרי הקצה:
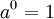 שכן יש פונקציה יחידה מהקבוצה הריקה לכל מקום - היחס שהוא הקבוצה הריקה.
שכן יש פונקציה יחידה מהקבוצה הריקה לכל מקום - היחס שהוא הקבוצה הריקה.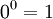 זה מקרה פרטי של הסעיף הקודם, ועדיין מתקיים
זה מקרה פרטי של הסעיף הקודם, ועדיין מתקיים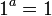
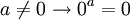 אין אף פונקציה מקבוצה לא ריקה אל קבוצה ריקה, שכן יחס כזה לא יכול להיות שלם.
אין אף פונקציה מקבוצה לא ריקה אל קבוצה ריקה, שכן יחס כזה לא יכול להיות שלם.
תכונות האריתמטיקה
יהיו a,b,c עוצמות אזי מתקיים
כלומר מתקיימים חוקי החזקות ה"רגילים"
נוכיח למשל 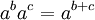 יהיו
יהיו 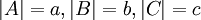 קבוצות זרות
נגדיר פונקציה מ
קבוצות זרות
נגדיר פונקציה מ 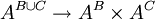 ע"י
ע"י 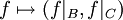 . היא חח"ע ועל.
. היא חח"ע ועל.
נוכיח למשל 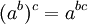 יהיו
יהיו 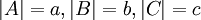 קבוצות זרות
נגדיר פונקציה מ
קבוצות זרות
נגדיר פונקציה מ 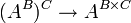 ע"י
ע"י 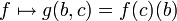 . היא חח"ע ועל.
. היא חח"ע ועל.
בנוסף אם מניחים את אקסיומת הבחירה אזי מתקיים עבור a,b עוצמות כאשר אחד מהם אין סופי
-
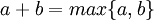
- אם שניהם אינם אפס אזי
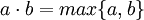
- מסקנה: אם
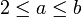 אזי
אזי 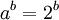
הוכחה 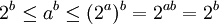
תרגיל
הוכח כי 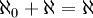
הוכחה: דרך א- ישירות מהגדרה. נבחר ![A=[\frac{1}{4},\frac{1}{2}],B=\mathbb{N}](/images/math/d/1/3/d13abcc222b0c15a4a83d85900c1a541.png) אזי
אזי
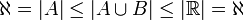
דרך ב- מהנוסחא. 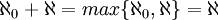
תרגיל
הוכח כי 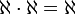
הוכחה: 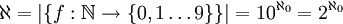
דרך א- ישירות מהגדרה. נבחר 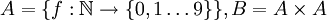 אזי
נגדיר פונקציה
אזי
נגדיר פונקציה 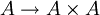 ע"י
ע"י 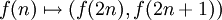 . זו פונקציה חח" ועל.
. זו פונקציה חח" ועל.
דרך ב- אריתמטיקה-
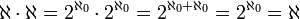
דרך ג- מהנוסחא- 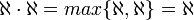
תרגיל
הוכח כי 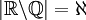
פתרון:
כיוון ש 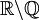 מוכל בממשיים עוצמתה לכל היותר אלף. נניח בשלילה כי עוצמתה שווה a קטנה ממש מאלף אזי
מוכל בממשיים עוצמתה לכל היותר אלף. נניח בשלילה כי עוצמתה שווה a קטנה ממש מאלף אזי
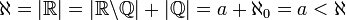 . סתירה
. סתירה
תרגיל
חשבו את 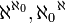
פתרון: 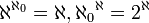
הסיקו כי עוצמת קבוצת הפונקציות מהרציונאלים לממשיים היא 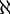 .
.
תרגיל
תהא  קבוצה אינסופית ו
קבוצה אינסופית ו 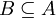 תת קבוצה.
תת קבוצה.
הוכח/הפרך
1. 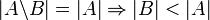
2. 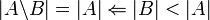
פתרון:
1. הפרכה: ניקח את השלמים והטבעיים
2. נכון כי ניתן להציג A כאיחוד זר 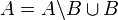 ולכן
ולכן 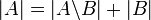 . אם
. אם 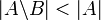 נקבל סתירה
נקבל סתירה
תרגיל
1. מה עוצמת 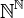
פתרון: 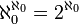
2. מה עוצמת 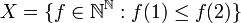
פתרון: לכל היותר 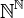 ולכל הפחות
ולכל הפחות 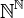 כי לכל
כי לכל 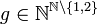 נתאים
נתאים 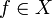 ע"י
ע"י 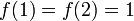 ועבור
ועבור 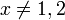 נגדיר
נגדיר 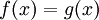 ולכן
ולכן 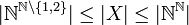 ולפי ק.ש.ב יש שיווון
ולפי ק.ש.ב יש שיווון
3. מה עוצמת 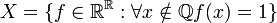
פתרון: X שווה עוצמה ל 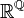 כי
כי 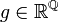 ממופה ל
ממופה ל 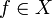 המוגדרת
המוגדרת 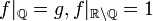
תרגיל
תהי 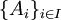 משפחה של קבוצות הזרות זו לזו כך שעוצמת כל אחת מהן ב
משפחה של קבוצות הזרות זו לזו כך שעוצמת כל אחת מהן ב . נגדיר
. נגדיר 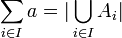 .
הוכח כי
.
הוכח כי 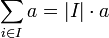
פתרון:
תהא  קבוצה נוספת מעוצמה
קבוצה נוספת מעוצמה  .
לכל
.
לכל 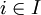 קיימת פונקציה חח"ע ועל
קיימת פונקציה חח"ע ועל
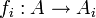 .
כעת נגדיר פונקציה
.
כעת נגדיר פונקציה 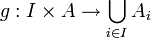 ע"י
ע"י 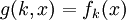 . מכיוון שהקבוצות זרות ו
. מכיוון שהקבוצות זרות ו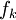 חח"ע ברור שg חח"ע. מכיוון ש
חח"ע ברור שg חח"ע. מכיוון ש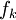 על גם g על ולכן קיבלנו את המבוקש.
על גם g על ולכן קיבלנו את המבוקש.
תרגיל
נגדיר 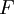 להיות אוסף תתי הקבוצות הסופיות של הטבעיים
להיות אוסף תתי הקבוצות הסופיות של הטבעיים 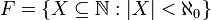 . מה עוצמתה?
. מה עוצמתה?
פתרון: לכל 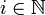 נגדיר
נגדיר 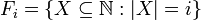 (אוסף תתי הקבוצות מגודל
(אוסף תתי הקבוצות מגודל 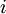 ). אזי
). אזי 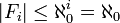 ואז
ואז 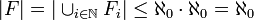
תרגיל (בש.ב.)
נגדיר  להיות אוסף תתי הקבוצות האינסופיות של הטבעיים. מה עוצמתה?
להיות אוסף תתי הקבוצות האינסופיות של הטבעיים. מה עוצמתה?
פתרון: מתקיים כי 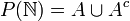 כאשר A היא תתי הקבוצות הסופיות מתרגיל קודם שעוצמת
כאשר A היא תתי הקבוצות הסופיות מתרגיל קודם שעוצמת 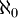 ולכן
ולכן 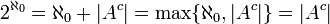
תרגיל
נגדיר 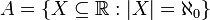 ,מה עוצמתה?
,מה עוצמתה?
פתרון: לכל הפחות 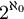 כי תתי הקבוצות האינסופיות של הטבעיים מעוצמה זאת. בצד שני נגדיר
כי תתי הקבוצות האינסופיות של הטבעיים מעוצמה זאת. בצד שני נגדיר 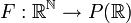 ע"י
ע"י
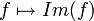 טענה:
טענה: 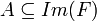 הוכחה: תהא
הוכחה: תהא 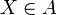 ומהגדרת A, נסיק כי X מעוצמה הטבעיים ולכן קיימת
ומהגדרת A, נסיק כי X מעוצמה הטבעיים ולכן קיימת 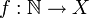 חח"ע ועל ולכן
חח"ע ועל ולכן 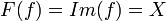 . מסקנה מכך
. מסקנה מכך 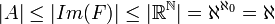 . לפי ק.ש.ב
. לפי ק.ש.ב 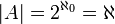
תרגיל
נגדיר 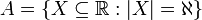 ,מה עוצמתה?
,מה עוצמתה?
פתרון: לכל היותר 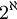 מצד שני
מצד שני 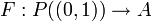 המוגדרת
המוגדרת 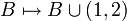 חח"ע ולפי ק.ש.ב. סימנו
חח"ע ולפי ק.ש.ב. סימנו
תרגיל ממבחן תשסח מועד א (ד"ר שי סרוסי וד"ר אלי בגנו)
תהי A קבוצה אינסופית. נסמן 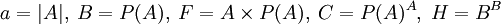
- א. מצא את
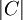
- ב. מצא את
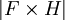
- ג. מצא את
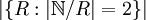 המוכלת באוסף יחסי השקילות על הטבעיים.
המוכלת באוסף יחסי השקילות על הטבעיים.
פתרון.
א. 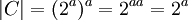
ב.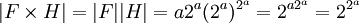
ג. כל יחס שקילות שקבוצת המנה 2 מתאים לחלוקה של 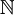 ל-2 קבוצות זרות.
ולכן יש התאמה חח"ע ועל
ל-2 קבוצות זרות.
ולכן יש התאמה חח"ע ועל 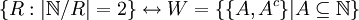 ולכן 2 הקבוצות מאותה עוצמה.
ולכן 2 הקבוצות מאותה עוצמה.
ט: 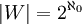
ה: נסמן 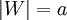 . בנוסף
. בנוסף 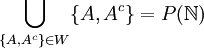 ולכן
ולכן 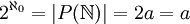 .
.
תרגיל
נגדיר 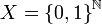 קבוצת כל הסדרות הבינאריות. נגדיר יחס
קבוצת כל הסדרות הבינאריות. נגדיר יחס 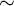 על
על 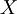 כך
כך 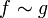 אמ"מ הקבוצה
אמ"מ הקבוצה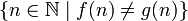 סופית
סופית
הוכיחו כי 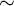 יח"ש
יח"ש
לכל 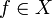 , מצאו את העוצמה של
, מצאו את העוצמה של ![[f]](/images/math/7/b/9/7b93cec8a8b3e110392556212941efcd.png) .
.
מצאו את העוצמה של קבוצת המנה.
תרגיל
תהא 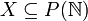 .
.
מצאו 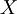 המקיימת: כל
המקיימת: כל 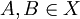 שונות הן זרות (כלומר
שונות הן זרות (כלומר 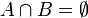 ).
).
ניח 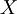 מקיימת: כל
מקיימת: כל 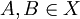 שונות הן זרות. הוכיחו כי
שונות הן זרות. הוכיחו כי 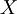 בת מנייה.
בת מנייה.
תהא 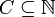 . נניח
. נניח 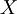 מקיימת: החיתוך של
מקיימת: החיתוך של 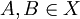 שונות הוא
שונות הוא 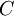 (כלומר
(כלומר 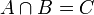 ). הוכיחו כי
). הוכיחו כי 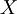 בת מנייה.
בת מנייה.
נניח 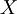 מקיימת: החיתוך של
מקיימת: החיתוך של 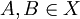 שונות הוא לכל היותר בן 10 איברים (כלומר
שונות הוא לכל היותר בן 10 איברים (כלומר 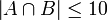 ). הוכיחו כי
). הוכיחו כי 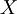 בת מנייה.רמז:
בת מנייה.רמז: 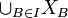 כאשר
כאשר 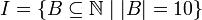 ו
ו 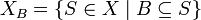
תרגיל ממבחן תשע מועד א (ד"ר שי סרוסי וד"ר אפי כהן)
יהי S יחס על 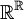 (קבוצת כל הפונקציות הממשיות), המוגדר על ידי
(קבוצת כל הפונקציות הממשיות), המוגדר על ידי 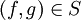 אם"ם לכל
אם"ם לכל 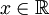 מתקיים
מתקיים 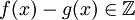
- 1. הוכיחו ש S הינו יחס שקילות
- 2. תהי
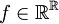 מצאו את
מצאו את ![|[f]|](/images/math/0/1/3/01364e045ffa77dc9f947de382b72c71.png)
- 3. מצאו את
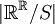
פתרון:
1.
- רפלקסיביות:
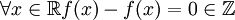
- סימטריות:
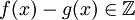 גורר שגם
גורר שגם 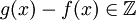 כי יש נגדי לחיבור
כי יש נגדי לחיבור - טרנזיטיביות: נובעת בקלות מסגירות לחיבור בשלמים:
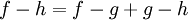
2.
עבור ![[f]\in \mathbb{R}^\mathbb{R}/S](/images/math/0/f/4/0f474b6e386c525018e9212885912aea.png) נגדיר
נגדיר ![F:[f] \to \mathbb{Z}^{\mathbb{R}}](/images/math/b/e/e/beecd5a9f541c3eabc025b24717e1ea5.png) .
ע"י
.
ע"י 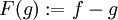 נראה כי היא מוגדרת,חח"ע ועל.
נראה כי היא מוגדרת,חח"ע ועל.
מוגדרת: לפי ההגדרה של יחס השקילות אכן מתקיים 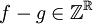
נראה כי ל F קיימת הופכית. נגדיר ![G: \mathbb{Z}^{\mathbb{R}} \to [f]](/images/math/8/3/5/83584cccb15969f10a2bf56e16a919bf.png) . ע"י
. ע"י 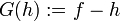 . הפונקציה מוגדרת היטב כי
. הפונקציה מוגדרת היטב כי 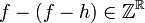 וקל לוודא שזוהי ההופכית
וקל לוודא שזוהי ההופכית
חח"ע: נניח 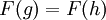 לכן
לכן 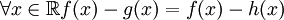 ולכן h=g.
ולכן h=g.
על: תהי h פונקציה כלשהי מהממשיים לשלמים, ברור ש(f-h) במחלקת השקילות של f והיא תהיה המקור.
אם כך, העוצמה של מחלקת השקילות זהה לעוצמה של אוסף הפונקציות מהממשיים לשלמים והוא 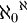 . לפי התכונות שלמדנו לעיל מתקיים
. לפי התכונות שלמדנו לעיל מתקיים 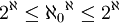 ולכן לפי קנטור מתקיים
ולכן לפי קנטור מתקיים 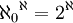
3.
נזכור בסימון 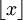 שהוא המספר השלם הגדול ביותר הקטן או שווה לx.
שהוא המספר השלם הגדול ביותר הקטן או שווה לx.
נגדיר F פונקציה השולחת את 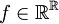 לפונקציה
לפונקציה 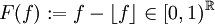 . נראה ש-F מוגדרת היטב (על קבוצת המנה)וההפעלה שלה על קבוצת המנה תהיה חח"ע ועל.
. נראה ש-F מוגדרת היטב (על קבוצת המנה)וההפעלה שלה על קבוצת המנה תהיה חח"ע ועל.
מוגדרות: יהיו שתי פונקציות באותה מחלקת שקילות g,f. אזי, 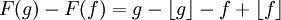 . מכיוון שזהו הפרש של שני מספרים אי שליליים קטנים מאחד, זה שווה למספר שבערכו המוחלט קטן מאחד. מכיוון שההפרש בין f ל-g שלם, המספר הזה הוא שלם. המספר השלם האי שלילי היחיד שקטן מאחד הינו אפס
כלומר
. מכיוון שזהו הפרש של שני מספרים אי שליליים קטנים מאחד, זה שווה למספר שבערכו המוחלט קטן מאחד. מכיוון שההפרש בין f ל-g שלם, המספר הזה הוא שלם. המספר השלם האי שלילי היחיד שקטן מאחד הינו אפס
כלומר 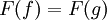 . לכן הפונקציה F מוגדרת היטב שכן היא שולחת נציגים שונים של מחלקת שקילות לאותו מקום.
. לכן הפונקציה F מוגדרת היטב שכן היא שולחת נציגים שונים של מחלקת שקילות לאותו מקום.
חח"ע: נניח 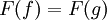 אז
אז 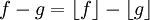 כיוון ש
כיוון ש 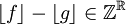 אזי הם נציגים של אותה מחלקת שקילות כלומר
אזי הם נציגים של אותה מחלקת שקילות כלומר ![[f]=[g]](/images/math/4/6/6/46691983add002759ec9845017a9a9e4.png)
על: ניקח פונקציה כלשהי r מהממשיים לקטע 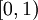 . קל לראות ש
. קל לראות ש ![F[r]=r](/images/math/d/c/4/dc489fd8ed8f9693b75a3b47a0736eda.png) שכן
שכן
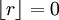 . לכן r ישמש מקור ולכן F הינה על.
. לכן r ישמש מקור ולכן F הינה על.
סה"כ קיבלנו שעוצמת קבוצת המנה שווה ל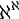 וזה שווה ל
וזה שווה ל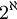 לפי התכונות לעיל.
לפי התכונות לעיל.
תרגיל ממבחן תשע מועד ב (ד"ר שי סרוסי וד"ר אפי כהן)
א. תהי A קבוצה אינסופית מעוצמה a.
- 1. נגדיר עבור :
![X=\{(X_1,...,X_n):1<n\in\mathbb{N}\and\Big[\bigcup_i X_i=A\Big] \and \Big[\forall i\neq j: X_i\cap X_j = \emptyset\Big] \and \big[ \forall i X_i \neq \emptyset\big]\}](/images/math/7/9/7/797065eef6aa5d000ce8f4fd3183b46a.png) .
.
כלומר אוסף החלקות הסופיות הלא טרי' הסדורות של A
הוכח 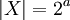
- 2. מצא את
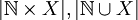 וגם את
וגם את 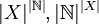
ב.תהי 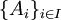 משפחה של קבוצות הזרות זו לזו. נסמן את עוצמת כל אחת מהן ב
משפחה של קבוצות הזרות זו לזו. נסמן את עוצמת כל אחת מהן ב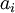 בהתאמה. נגדיר
בהתאמה. נגדיר 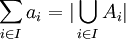 .
.
חשב את 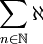
פתרון.
א.
- 1.
נביט באוסף הפונקציות 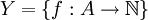 . נגדיר
. נגדיר 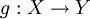 על ידי לכל
על ידי לכל 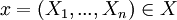
נשלח אותו ל 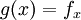 המוגדר
המוגדר
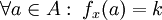 כאשר
כאשר 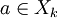 כלומר שולחת איבר לאינדקס של הקבוצה שהוא נמצא בה בחלוקה.
כלומר שולחת איבר לאינדקס של הקבוצה שהוא נמצא בה בחלוקה.
נוכיח שהפונקציה מוגדרת וחח"ע.
מוגדרת: כיוון ש x הוא חלוקה של A אזי האיבר a יופיע ויופיע בדיוק באחת מהקבוצות.
חח"ע: נניח 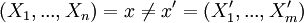 . אזי קיים
. אזי קיים 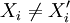 , לכן קיים יהיה
, לכן קיים יהיה 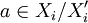 (או להיפך) ואז
(או להיפך) ואז 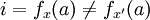 כלומר
כלומר 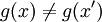
דרך 2- נגדיר פונקציה 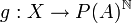 ע"י
ע"י 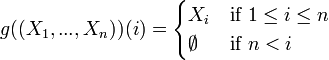
קל לראות כי הפונקציה חח"ע ולכן 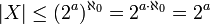
דרך 3- נציג את X כאיחוד זר 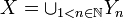 כאשר
כאשר 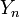 זה חלוקות סדורות של A עם n קבוצות. כעת לכל n קיימת פונקציה
זה חלוקות סדורות של A עם n קבוצות. כעת לכל n קיימת פונקציה 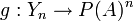 המוגדרת
המוגדרת 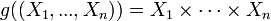 קל לראות שהיא חח"ע ולכן
קל לראות שהיא חח"ע ולכן 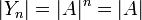 ולכן
ולכן 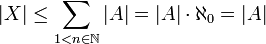
כעת, קל למצוא פונקציה חח"ע מקבוצת החזקה של A ל-X - נשלח כל תת קבוצה לזוג שמכיל אותה ואת המשלים שלה.
לכן 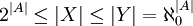 , ולפי התכונות לעיל שני הקצוות שווים. לכן עוצמת X הינה
, ולפי התכונות לעיל שני הקצוות שווים. לכן עוצמת X הינה 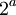 .
.
- 2.
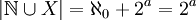
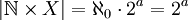
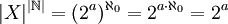
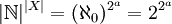
ב.
בעצם אנו רוצים לחשב איחוד בן מנייה של קבוצות מעוצמת 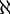 .
לכל עותק של
.
לכל עותק של 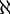 נתאים
נתאים 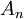 ופונקציה חח"ע ועל
ופונקציה חח"ע ועל
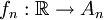 .
כעת נגדיר פונקציה
.
כעת נגדיר פונקציה 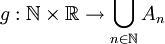 ע"י
ע"י 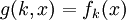 . מכיוון שהקבוצות זרות ו
. מכיוון שהקבוצות זרות ו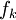 חח"ע ברור שg חח"ע. מכיוון ש
חח"ע ברור שg חח"ע. מכיוון ש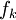 על גם g על ולכן סה"כ עוצמת הסכום הינה
על גם g על ולכן סה"כ עוצמת הסכום הינה