הבדלים בין גרסאות בדף "שיחה:89-214 סמסטר א' תשעא/תרגילים"
(←תרגיל 2 שאלה 5) |
(←איך מוכיחים \mathbb{Z}_{n}\times \mathbb{Z}_{m}\cong \mathbb{Z}_{gcd(n,m)) \times \mathbb{Z}_{lcm(n,m)}) |
||
| (103 גרסאות ביניים של 32 משתמשים אינן מוצגות) | |||
| שורה 2: | שורה 2: | ||
ראשית, קיראו את ההנחיות ב[[עמוד ראשי|עמוד הראשי]]. דף זה מיועד לשאלות בנוגע לתרגילים - כולל קושיות ותהיות מתמטיות, וגם סוגיות טכניות (לפחות עד שנגְלה את אלה לדף אחר). אנא אל תפתחו כותרות ראשיות שלא לצורך. [[משתמש:עוזי ו.|עוזי ו.]] 19:28, 7 באוקטובר 2010 (IST) | ראשית, קיראו את ההנחיות ב[[עמוד ראשי|עמוד הראשי]]. דף זה מיועד לשאלות בנוגע לתרגילים - כולל קושיות ותהיות מתמטיות, וגם סוגיות טכניות (לפחות עד שנגְלה את אלה לדף אחר). אנא אל תפתחו כותרות ראשיות שלא לצורך. [[משתמש:עוזי ו.|עוזי ו.]] 19:28, 7 באוקטובר 2010 (IST) | ||
| − | |||
| − | |||
== נושאים כלליים == | == נושאים כלליים == | ||
| + | * האם בהרכבת של פעולה בינארית יכול להיות תנאי? לדוגמה: | ||
| + | a, b שייכים ל N | ||
| + | |||
| + | a + b = | ||
| + | 1 אם a זוגי | ||
| − | + | אחרת 2 | |
| + | : בוודאי שהגדרת הפעולה יכולה להיות מסובכת; פעולה בינארית מתאימה ערך לכל זוג סדור. אין שום סיבה לצפות שהפעולה תהיה מורכבת מפעולות מוכרות. [[משתמש:עוזי ו.|עוזי ו.]] 20:44, 6 בנובמבר 2010 (IST) | ||
| − | + | * רוצים לכתוב נוסחאות מתמטיות כאן ולא יודעים איך? אתם יכולים להעזר בעורך LaTeX הבא: | |
| + | http://www.codecogs.com/latex/eqneditor.php | ||
| + | זה גם עוזר ללמוד קצת LaTeX, תוך כדי, אבל לא חייבים להפנים אם לא רוצים. כדי להכניס את הנוסחה שערכתם, בעת עריכת ההודעה לחצו על ה-<math>\sqrt{n}</math> שמופיע ב-toolbar מעל תיבת העריכה והדביקו את הנוסחה במקום הטקסט formula שיופיע. | ||
| + | --[[מיוחד:תרומות/84.110.186.131|84.110.186.131]] 15:57, 22 בנובמבר 2010 (IST) | ||
| − | האם | + | * במשפט האיזומורפיזם הראשון אמרנו כי לכל הומומורפיזם <math>\ \phi : G \rightarrow H</math>, <math>\ G/\operatorname{Ker}(\phi) \cong \operatorname{Im}(\phi)</math>. האם גם הכיוון השני נכון? כלומר, האם זה נכון כי אם <math>G/N\cong K</math> אז קיים אפימורפיזם <math>\phi: G\rightarrow K</math> שהגרעין שלו הוא <math>N</math>? --[[משתמש:Shwarto|Shwarto]] 17:56, 5 בדצמבר 2010 (IST) |
| + | :* בהחלט: ההעתקה <math>\ g \mapsto gN</math> היא אפימורפיזם. [[משתמש:עוזי ו.|עוזי ו.]] 22:03, 20 בינואר 2011 (IST) | ||
| + | ::* אז למעשה זה בשני שלבים, לפי מה שאני מבין. קודם מעתיקים לחבורת המנה <math>G/N</math>. מכיוון שהיא איזומורפית ל-<math>K</math>, עפ"י ההנחה, אז קיים איזומורפיזם מ-<math>G/N</math> ל-<math>K</math> ואז ההרכבה של ההעתקות האלה היא אותו אפימורפיזם <math>\phi: G\rightarrow K</math> שהגרעין שלו הוא <math>N</math> שרציתי לדעת אם הוא קיים. תודה. --[[משתמש:Shwarto|Shwarto]] 17:56, 22 בינואר 2011 (IST) | ||
| − | + | * לגבי '''תרגיל 7''', כתוב למעלה שהקבוצה של יום רביעי (קבוצה 5) צריכה להגיש את התרגיל עד ה-22/12 ואח"כ כתוב שעד 26/12 בשעה 12:00 לתא של מיכאל. מה נכון? | |
| + | --[[מיוחד:תרומות/84.110.207.119|84.110.207.119]] 23:22, 19 בדצמבר 2010 (IST) | ||
| + | :יש שתי קבוצות ביום רביעי (04, 05). קבוצה 04 מגישה כרגיל (22/12), קבוצה 05 מגישה עד 26/12. [[משתמש:דורון פרלמן|דורון פרלמן]] 00:57, 20 בדצמבר 2010 (IST) | ||
| − | |||
| − | == תרגיל 2 שאלה 2 == | + | * כמה תרגילים צריך להגיש סה"כ? תודה. |
| + | :7. [[משתמש:דורון פרלמן|דורון פרלמן]] 21:03, 6 בינואר 2011 (IST) | ||
| + | |||
| + | === שאלה על משפט המיון === | ||
| + | |||
| + | אפשר לקבל הסבר למשפט הבא: | ||
| + | כל חבורת P אבלית איזומורפית למכפלה ישרה של חבורות P ציקליות | ||
| + | : ראשית, יש לדייק: השימוש באות P כדי לסמן מספר ראשוני עלול לבלבל. צריך להיות "כל חבורת-p אבלית איזומורפית למכפלה ישרה של חבורות-p ציקליות". "חבורת-p" (כאשר p הוא מספר ראשוני) היא חבורה שהסדר של כל איבר שלה הוא '''חזקה''' של p. לפי משפט קושי, חבורה סופית היא חבורת-p אם ורק אם הסדר שלה הוא חזקה של p בעצמו. בפרט, חבורת-p ציקלית היא חבורה מהצורה <math>\ \mathbb{Z}_{p^m}</math> לאיזשהו m. | ||
| + | : אם כך, הטענה היא שכל חבורת-p אבלית איזומורפית למכפלה של חבורות-p ציקליות. מה לא ברור? [[משתמש:עוזי ו.|עוזי ו.]] 22:01, 20 בינואר 2011 (IST) | ||
| + | :: למה יש צורך לציין כי מדובר בחבורת-p '''אבלית'''? האם לא כל חבורה שהיא מסדר חזקה של ראשוני היא איזומורפית ל-<math>\mathbb{Z}_{p}</math> ולכן אבלית? | ||
| + | ::: כאשר משתמשים במושג "חבורת-p" הכוונה היא לחבורה שהסדר שלה הוא p^n, ולא כל חבורה מסדר זה היא אבלית (למשל, ראינו חבורות לא אבליות מסדר p^3: מטריצות משולשיות עליונות עם 1 באלכסון ושאר הכניסות ב- <math>\mathbb{Z}_{p}</math>). מיכאל. | ||
| + | ::: יש לך בלבול כלשהו. ננסה לעשות סדר. מה שאנחנו יודעים זה שכל חבורה שהיא מסדר ראשוני היא ציקלית, ושכל חבורה ציקלית מסדר n איזומורפית ל-<math>\mathbb{Z}_{n}</math>, לכן יש חבורה יחידה מכל סדר p (ראשוני) והיא <math>\mathbb{Z}_{p}</math>. בנוגע לחזקות של ראשוניים (במקרה הכללי) אנחנו לא יודעים הרבה (כן הוכחנו כמה תוצאות, למשל שהמרכז הוא לא טריוואלי, אבל ממש לא אפיינו את כל החבורות האלה). את/ה שואל/ת "האם לא כל חבורה שהיא מסדר חזקה של ראשוני היא איזומורפית ל-<math>\mathbb{Z}_{p}</math> ולכן אבלית"? ודאי שלא! ראשית, איך חבורה שהיא מסדר חזקה של ראשוני יכולה להיות איזומורפית ל-<math>\mathbb{Z}_{p}</math>? למשל איך חבורה מסדר 9 יכולה להיות איזומורפית ל-<math>\mathbb{Z}_{3}</math>? באחת יש 9 איברים ובשניה 3 איברים! מעבר לזה, ראינו שיש 5 חבורות מסדר 8 (ו-8 זה 2 בחזקת 3 לכן 8 היא חבורת-p עם p=2), ששתיים מהן לא אבליות (<math>D_{4}</math> וחבורת הקווטרניונים). לסיכום במקרה הלא אבלי אנחנו לא יודעים הרבה. במקרה האבלי אנחנו יודעים הכל: לפי המשפט שציטטת בראשית דיון זה. [[משתמש:דורון פרלמן|דורון פרלמן]] 19:21, 22 בינואר 2011 (IST) | ||
| + | ::::התכוונתי ''"כל חבורה שהיא מסדר חזקה של ראשוני היא איזומורפית ל-<math>\mathbb{Z}_{p^n}</math> ולכן אבלית"'', אבל אני מבין כעת שזו שטות גמורה בהנתן דוגמאות פשוטות כמו <math>D_{4}</math>. תודה.--[[מיוחד:תרומות/84.110.200.251|84.110.200.251]] 18:08, 23 בינואר 2011 (IST) | ||
| + | |||
| + | === שאלה === | ||
| + | U32 איזומורפי ל <3>*K. | ||
| + | האיבר 3 נבחר כי הוא מסדר האקספוננט, | ||
| + | איך בוחרים את התת חבורה הנוספת(את k)? | ||
| + | : ראשית, <math>\ K \neq k</math>. | ||
| + | : החבורה שלנו היא חבורת-2 (כלומר, חבורה שסדרה חזקה של 2; במקרה זה 16). מכיוון שהאיבר 3 מסדר השווה לאקספוננט, אפשר להפעיל את המשפט על פירוק של חבורה אבלית G למכפלה ישרה שאחד הגורמים שלה הוא חבורה ציקלית H מסדר האקספוננט (תמצית ההוכחה: בוחרים איבר מסדר p בחבורת המנה G/H, ומחליפים אותו באיבר מסדר p בחבורה G שאינו נמצא ב-H; האיבר הזה יוצר תת-חבורה Q. אחר-כך בונים את הפירוק הישר באינדוקציה בחבורה G/Q, ומרימים הכל ל-G). לחלופין, מכיוון שהסדר של 3 הוא 8, מספיק לבחור איבר מסדר 2 שאינו בתת-החבורה <math>\ \langle 3 \rangle</math>. [[משתמש:עוזי ו.|עוזי ו.]] 21:01, 22 בינואר 2011 (IST) | ||
| + | |||
| + | === אוטומורפיזמים === | ||
| + | |||
| + | *כאשר יש אוטומורפיזם מחבורה לעצמה שהוא לא הזהות האם בעצם מבחינה רעיונית זה אומר שיש 2 איברים או יותר שמתנהגים אותו הדבר אז אפשר להחליף בינהם? | ||
| + | : חסרה מלת קישור לפני "יש" או "אז". ("אם יש ... אז?", "יש ... ואז"?). תרגיל: מצאו את כל החבורות שבהן יש שני אברים שהחלפתם זה בזה (בלי לשנות אף איבר אחר) היא אוטומורפיזם. [[משתמש:עוזי ו.|עוזי ו.]] 21:03, 22 בינואר 2011 (IST) | ||
| + | |||
| + | ::*סליחה על הבלבול התכוונתי עם ו...אז. | ||
| + | ::: אז אני לא יודע למה הכוונה ב"אפשר להחליף ביניהם". אוטומורפיזם הוא סימטריה של החבורה - ואם הוא מעביר איבר אחד לאיבר אחר (ופועל באותו זמן על כל שאר החבורה, כמובן), זה אומר שאין דרך לזהות ביניהם באמצעות "שאלות חבורתיות"; זו לא חוכמה גדולה, כי האינווריאנט היחיד של '''איבר בודד''' הוא הסדר שלו. [[משתמש:עוזי ו.|עוזי ו.]] 02:04, 23 בינואר 2011 (IST) | ||
| + | |||
| + | === קבוצה יוצרת === | ||
| + | * אם עושים מתת-קבוצה S של חבורה G '''לא-אבלית''' קבוצה יוצרת (כמו שלמדנו) אז למה זה יוצא תת-חבורה? (אם G אבלית אני מבין) | ||
| + | :: כל תת-קבוצה (בכל חבורה) יוצרת, בהגדרה, את תת-החבורה הקטנה ביותר המכילה אותה. תת-החבורה הזו כוללת (בדיוק) את כל המכפלות שאפשר להרכיב מן הקבוצה היוצרת (והפכיהם), בכל סדר ובכל אורך שהוא. [[משתמש:עוזי ו.|עוזי ו.]] 02:06, 23 בינואר 2011 (IST) | ||
| + | תודה, אבל השאלה שלי היא למה יש סגירות לפעולה? | ||
| + | : כי תת-החבורה הנוצרת היא, בהגדרה, '''תת-החבורה''' הקטנה ביותר המכילה את הקבוצה. הסבר חלופי: מדובר באוסף '''כל''' המכפלות; אם מכפילים שתי מכפלות זו בזו, מתקבלת כמובן מכפלה חדשה (אולי ארוכה יותר). [[משתמש:עוזי ו.|עוזי ו.]] 20:35, 23 בינואר 2011 (IST) | ||
| + | |||
| + | === מאפיין של שדה=== | ||
| + | * כאשר נתון שדה עם סדר p בחזקת n,אז המאפיין הוא p.האם יוצא מז שכאשר מסתכלים על החבורה החיבורית של השדה,הסדר של כל איבר בשדה הוא p? | ||
| + | :: האקספוננט של החבורה החיבורית של שדה שווה למאפיין של השדה. [[משתמש:עוזי ו.|עוזי ו.]] 00:13, 24 בינואר 2011 (IST) | ||
| + | |||
| + | === "מתכון" לאוטומורפיזם === | ||
| + | הגדרנו לכל <math>g\in G</math> את הפונקציה <math>\gamma_{g}:G\rightarrow G</math> המוגדרת ע"י <math>\gamma_{g}(x)=gxg^{-1}</math> וטענו כי זה אוטומורפיזם. כמו כן, הגדרנו <math>\Gamma :G\rightarrow Aut(G)</math> לפי <math>\Gamma(g)=\gamma_{g}</math> וטענו כי <math>Inn(G)\doteq Im(\Gamma)\triangleleft Aut(G)</math>. האם נכון לומר כי הפונקציות <math>\gamma_{g}</math> אמנם מגדירות אוטומורפיזמים אך לא בהכרח את כל האוטומורפיזמים ולכן לא בהכרח מתקיים <math>Im(\Gamma)=Aut(G)</math>? כלומר, האופן בו הגדרנו את <math>\gamma_{g}</math> בסה"כ מגדיר לנו אוטומורפיזם אבל זו אינה שיטה לקבל את כל האוטומורפיזמים האפשריים. | ||
| + | אני מבין כי עבור חבורה אבלית זה לא חייב לתת את כל האוטומורפיזמים האפשריים כי לכל <math>g\in G</math> מתקיים <math>\gamma_{g} = Id</math> בעוד שאם לחבורה כזו יש יותר מיוצר אחד אז אפשר להעביר כל יוצר לכל יוצר אחר ואז לקבל אוטומורפיזם שונה - כלומר, לא רק את <math>Id</math>, אבל מה לגבי חבורות לא אבליות? | ||
| + | :: אתה צודק: לא בהכרח שחבורת האוטומורפיזמים הפנימיים תהיה חבורת כל האוטומורפיזמים. בנוסף, אתה יודע שבחבורה לא אבלית, <math>G > Z(G)</math>, ולכן חבורת המנה <math>G/Z(G)</math> איננה טריוויאלית. אבל חבורה זו איזומורפית לחבורת האוטומור' הפנימיים, ולכן בחבורה לא אבלית תמיד יש אוטומורפיזמים פנימיים. אם אינני טועה, השאלה אם עבור חבורה לא אבלית <math>G</math> מתקיים <math>Inn(G) = Aut(G)</math> כבר תלויה בחבורה עצמה. למשל, <math>Inn(S_6) = S_6</math> (למה? מהו המרכז של <math>S_6</math>?) אבל <math>Aut(S_6)</math> יותר גדולה מחבורת האוטומורפיזמים הפנימיים (זו טענה שקצת יותר קשה להוכיח). מיכאל. | ||
| + | :: אכן, בדרך כלל יש אוטומורפיזמים לא פנימיים. לגבי "חבורות אבליות עם יותר מיוצר אחד", הדברים שכתבת אינם מדוייקים. לחבורה ציקלית מסדר n יש <math>\ \phi(n)</math> אוטומורפיזמים, אבל המקרה הכללי יותר מורכב. אי אפשר סתם-כך לשלוח "כל יוצר ליוצר אחר". [[משתמש:עוזי ו.|עוזי ו.]] 13:10, 24 בינואר 2011 (IST) | ||
| + | |||
| + | === איך מוכיחים <math>\mathbb{Z}_{n}\times \mathbb{Z}_{m}\cong \mathbb{Z}_{gcd(n,m)} \times \mathbb{Z}_{lcm(n,m)}</math> === | ||
| + | * איך מוכיחים: Zn*Zm איזומורפי ל- Z(n,m)*Zlcm(n,m)? | ||
| + | : זו שאלה לא קלה בכלל. נסמן <math>\ d = (n,m)</math>, ונכתוב <math>\ d = \alpha n + \beta m</math>. מתברר ש- <math>\ (i,j) \mapsto (i-j,\frac{\beta m i + \alpha n j}{d})</math> הוא איזומורפיזם <math>\ \mathbb{Z}_n \times \mathbb{Z}_m \rightarrow \mathbb{Z}_{d} \times \mathbb{Z}_{\frac{nm}{d}}</math>. [[משתמש:עוזי ו.|עוזי ו.]] 13:35, 24 בינואר 2011 (IST) | ||
| + | *הצלחתי להוכיח מוגדרת היטב וחח"ע אבל לא הצלחתי להוכיח על... אפשר כיוון להוכחה? | ||
| + | *: החבורות בשני האגפים הן מאותו סדר, כך שאם ההעתקה חד-חד-ערכית היא גם על. [[משתמש:עוזי ו.|עוזי ו.]] 23:06, 22 בפברואר 2011 (IST) | ||
| + | |||
| + | === שאלה על מרכזים של תמורות=== | ||
| + | * באחת ההרצאות בכיתה, ניתנה הדוגמא כי <math>C_{S_4}\left ( (12)(34)\right ) = <(13)(24),(1324)></math>. | ||
| + | :הייתי מעוניין לדעת האם יש דרך לדעת את התשובה מבלי לרשום מפורשות את כל איברי S4 ולבדוק, או לחלופין כיצד הגענו לתשובה הזו. תודה. | ||
| + | |||
| + | יש כמה דרכים לחשב את המרכז של תמורה בחבורת הסימטריות. הדרך הקלה ביותר בדרך כלל היא להשתמש בחישוב על הצמדה, שלפיו כדי ש-x יתחלף עם (12)(34), צריך להתקיים השוויון <math>\ (12)(34) = (x(1) x(2)) (x(3) x(4))</math>. מכיוון שבשני האגפים מופיעים מחזורים זרים והפירוק למחזורים זרים הוא יחיד, ה"פתרון" למשוואה הזו הוא או <math>\ (12)=(x(1)x(2)), (34)=(x(3),x(4))</math> או להיפך; ובכל מקרה יש ארבעה פתרונות ל-x. [[משתמש:עוזי ו.|עוזי ו.]] 23:04, 22 בפברואר 2011 (IST) | ||
| + | |||
| + | === ציון בקורס === | ||
| + | האם צריך ציון עובר במבחן ובתרגול בנפרד, או שאם ביחד זה עובר אז זה מספיק (למרות שבמבחן הציון פחות מ-60)? | ||
| + | : הציון הקובע הוא הממוצע המשוקלל. [[משתמש:עוזי ו.|עוזי ו.]] 23:04, 22 בפברואר 2011 (IST) | ||
| + | |||
| + | == תרגיל 1 == | ||
| + | |||
| + | == תרגיל 2 == | ||
| + | |||
| + | === שאלה 2 === | ||
מהו X, הכוונה לכל X. X שייך לB, | מהו X, הכוונה לכל X. X שייך לB, | ||
| שורה 27: | שורה 102: | ||
הוא להסתכל על קבוצת כל הביטויים מהצורה <math>s+tx</math> כאשר הכפל (הפעולה) ביניהם מוגדר כפי שהוא מוגדר בשאלה (מיכאל פרידמן). | הוא להסתכל על קבוצת כל הביטויים מהצורה <math>s+tx</math> כאשר הכפל (הפעולה) ביניהם מוגדר כפי שהוא מוגדר בשאלה (מיכאל פרידמן). | ||
| − | == | + | === שאלה 5 === |
| + | |||
| + | האם בנוסף להנחות בשאלה מותר להניח כי: | ||
| + | |||
| + | <math>\frac{1}{\infty}=0</math>? | ||
| + | |||
| + | -- כן (מיכאל פרידמן) | ||
| + | |||
| + | === שאלה 6 === | ||
כדי להוכיח שהקבוצה היא מונואיד (מלבד סגירות ואבר יחידה) מספיק לומר שהרכבת טרספו' לינאריות היא אסוציאטיבית או שצריך ממש להוכיח את זה? (איך מוכיחים דבר כזה?!) | כדי להוכיח שהקבוצה היא מונואיד (מלבד סגירות ואבר יחידה) מספיק לומר שהרכבת טרספו' לינאריות היא אסוציאטיבית או שצריך ממש להוכיח את זה? (איך מוכיחים דבר כזה?!) | ||
: העתקות ליניאריות הן פונקציות. הרכבה של פונקציות היא תמיד אסוציאטיבית. [[משתמש:עוזי ו.|עוזי ו.]] 21:51, 26 באוקטובר 2010 (IST) | : העתקות ליניאריות הן פונקציות. הרכבה של פונקציות היא תמיד אסוציאטיבית. [[משתמש:עוזי ו.|עוזי ו.]] 21:51, 26 באוקטובר 2010 (IST) | ||
| + | |||
| + | === שונות === | ||
| + | |||
| + | שאלה כללית לגבי תרגיל 2 - | ||
| + | כשאני מנסה להוכיח האם קבוצה היא חבורה למחצה, | ||
| + | האם עליי להוכיח סגירות ואסוציאטיביות או שמספיק להוכיח רק אסוצ'? | ||
| + | : פורמלית, קבוצה אינה יכולה להיות חבורה למחצה: חבורה למחצה היא מערכת מתמטית הכוללת שני מרכיבים - קבוצה ופעולה בינארית. ופעולה, מעצם טיבה, היא "סגורה". לכן, אם נתונות קבוצה ופעולה, די להוכיח שהפעולה אסוציאטיבית. אם נתונות קבוצה ו"הצעה לפעולה", יש לבדוק שהפעולה אכן מוגדרת היטב, ואז שהיא גם אסוציאטיבית. | ||
| + | : לפעמים יש ברקע חבורה למחצה A עם פעולה משלה, ויש לבדוק האם תת-קבוצה B מהווה חבורה למחצה. במקרה כזה הכוונה היא לפעולה המצומצמת מ-A, כלומר לפונקציה המחזירה עבור שני אברים של B את המכפלה שלהם ב-A; א-פריורי, הפונקציה הזו עלולה להחזיר איברים של A שאינם ב-B, ואז היא אינה פעולה. הפונקציה '''מוגדרת היטב''' על B אם היא מחזירה ערך ב-B לכל שני אברים של B (כלומר, אם הקבוצה B סגורה ביחס לפעולה). מאידך, את האסוציאטיביות אין צורך לבדוק בנפרד, משום שהיא מתקבלת בירושה מ-A. [[משתמש:עוזי ו.|עוזי ו.]] 22:26, 31 באוקטובר 2010 (IST) | ||
| + | |||
| + | :: לא הבנתי איך אני מבדילה בתרגיל שקיבלנו (למשל בשאלה 1) בין פעולה "נתונה" ל"הצעה לפעולה"? --[[מיוחד:תרומות/93.172.3.238|93.172.3.238]] 03:00, 1 בנובמבר 2010 (IST) | ||
| + | :::יש לבדוק גם סגירות. [[משתמש:דורון פרלמן|דורון פרלמן]] 03:52, 1 בנובמבר 2010 (IST) | ||
| + | ::: לא כל מה שאומר "אני פעולה" הוא פעולה. לדוגמא, בסעיף ג' של שאלה 1 מבקשים שתוכיחו שהקבוצה <math>\ H=\{(x,y) \in \mathbb{Z}^2 | x^2-3y^2=1\}</math> עם ה"פעולה" <math>\ (x,y)*(z,w) = (xz+3yw,xw+yz)</math> היא חבורה למחצה. הצעד הראשון הוא לבדוק שזו באמת פעולה, כלומר, שהיא מחזירה איברים של H (ולא סתם זוגות סדורים). זו הסגירות המפורסמת. (ואכן, מה אם היו מבקשים לבדוק ש-H חבורה למחצה "תחת פעולת חיבור הוקטורים"?) אחריה, המועמד-לפעולה מקבל קידום ונעשה פעולה לכל דבר ועניין (ואז יש לבדוק שהיא אסוציאטיבית). [[משתמש:עוזי ו.|עוזי ו.]] 11:37, 1 בנובמבר 2010 (IST) | ||
| + | |||
| + | == תרגיל 3 == | ||
| + | |||
| + | * נניח שאני רוצה להגדיר חבורה (*,G). האם מותר לי לבנות את G כ-n-יה כאשר n הוא אינסוף? | ||
| + | [[מיוחד:תרומות/80.74.111.178|80.74.111.178]] 13:49, 7 בנובמבר 2010 (IST) | ||
| + | :כן. אני מניח שהתכוונת שכל אחד מאיברי G הוא n-יה אינסופית. ל-"n-יה אינסופית" קוראים בדרך כלל "סדרה" (שזו פשוט פונקציה שהתחום שלה הוא <math>\mathbb{N}</math>). בכל אופן אתה יכול להגדיר את G בכל דרך שתרצה, כל עוד הכל מוגדר היטב. [[משתמש:דורון פרלמן|דורון פרלמן]] 17:11, 7 בנובמבר 2010 (IST) | ||
| + | |||
| + | |||
| + | * שאלה 4: | ||
| + | מה הכוונה <math>sl(f) < gl(f)</math>? | ||
| + | למדנו יחס סדר בין חבורות? | ||
| + | ** הכוונה היא לאו דווקא ליחס סדר (אם כי אני לא לגמרי בטוח שזה לא מתקיים). כאן, הכוונה בביטוי <math>SL_n(\mathbb F) < GL_n(\mathbb F)</math> היא ש-<math>SL_n(\mathbb F)</math> היא תת-חבורה ("ממש") של <math>GL_n(\mathbb F)</math>. כלומר, <math>SL_n(\mathbb F)</math> היא חבורה שכל איבריה מוכלים ממש ב-<math>GL_n(\mathbb F)</math> כאשר הפעולה בשתי החבורות היא אותה פעולה. --[[משתמש:Shwarto|Shwarto]] 23:59, 8 בנובמבר 2010 (IST) | ||
| + | |||
| + | |||
| + | == תרגיל 4 == | ||
| + | |||
| + | === שאלה 1 === | ||
| + | * בסעיף א, מה הכוונה "חבורת המטריצות ההפיכות כאשר הכניסות הן ב-Z2"? זאת לא אמורה להיות חבורת המטריצות ההפיכות מגודל 2*2 מעל Z2? | ||
| + | ומעל איזו פעולה מדובר? | ||
| + | [[מיוחד:תרומות/93.172.153.180|93.172.153.180]] 15:28, 22 בנובמבר 2010 (IST) | ||
| + | **הכוונה היא שאיברי המטריצה הם ב-<math>\mathbb{Z}_2</math>. הפעולה היא כפל מטריצות. --[[מיוחד:תרומות/84.110.186.131|84.110.186.131]] 15:46, 22 בנובמבר 2010 (IST) | ||
| + | |||
| + | |||
| + | == תרגיל 5 == | ||
| + | |||
| + | * בשאלה 2 סעיף ב לא מנוסח באופן חד משמעי, האם הכוונה שלחבורה G אין תת חבורות נוספות כלל פרט לH? (הרי יש לפחות את הטריוויאליות). האם הכוונה שמסדר n אין עוד ת"ח לG פרט לH? מי הוא n? האם ניתן להניח כי <math>1<n<|G|</math> ? אולי הכוונה בכלל ש <math>|G|=n</math> ? (ואז אין בעצם כל כך מה להוכיח). אשמח להבהרות שיסבירו באופן חד משמעי מה השאלה פה. | ||
| + | ::*ניסוח יותר טוב: הוסף בתחילת הסעיף "יהי n ב-<math>\mathbb{N}</math>". (ובמילים אחרות: אתה צריך להראות שאם יש תת-חבורה כך שאין עוד תת-חבורות מאותו הסדר, אז היא נורמלית.) - דורון | ||
| + | * בשאלה 7 נתון שהחבורות <math>G_1\subseteq G_2\subseteq ...\subseteq G_n\subseteq...</math> פשוטות ויש להוכיח כי <math>G=\bigcup_{n}G_n</math> פשוטה. זה הרי נתון שהיא פשוטה, לא? כתוב על כל אחת מהן שהן פשוטות ושהן מוכלות אחת בשניה, אז האיחוד הזה הוא ממילא אותה חבורה עצמה שנתון שהיא פשוטה. לא ברור לי מה יש להוכיח כאן. | ||
| + | ::*לא הבנתי את כוונתך. "האיחוד הזה הוא ממילא אותה חבורה עצמה" - איזו חבורה עצמה? לא נתון כי G פשוטה. אתה צריך להוכיח כי היא פשוטה. [[משתמש:דורון פרלמן|דורון פרלמן]] 19:29, 27 בנובמבר 2010 (IST) | ||
| + | :::*אם הבנתי נכון, אני צריך להראות שלכל n, האיחוד הנ"ל הוא חבורה פשוטה, אבל נתון שכל <math>G_i</math> היא פשוטה. מהנתון, גם ברור כי <math>G_n</math> שווה לאיחוד של כל ה-<math>G_i</math> עבור i שקטן מ-n או שווה לו, כי היא מכילה אותם. אז בעצם ברור כי<math>G= G_n</math>, והרי נתון ש-<math>G_n</math> פשוטה, אז לא ברור לי מה יש להוכיח.--[[מיוחד:תרומות/84.110.206.83|84.110.206.83]] 09:54, 28 בנובמבר 2010 (IST) | ||
| + | ::::*עבור איזה n '''בדיוק''' מתקיים לדעתך <math>G=G_n</math>. עבור 10? 100? 1000? הרי כל G_n עשוייה להוסיף איברים חדשים, אין פה שום חבורה אחרונה. --[[משתמש:ארז שיינר|ארז שיינר]] 12:13, 28 בנובמבר 2010 (IST) | ||
| + | :::::*אז הכוונה היא להוכיח שזה נכון לכל n (וזה עדיין משהו שנתון)? או שעבור <math>n=\infty</math>? שגם זה משהו שלא כ"כ ברור לי.--[[מיוחד:תרומות/84.110.206.83|84.110.206.83]] 13:31, 28 בנובמבר 2010 (IST) | ||
| + | ::::::*יש להוכיח לאיחוד של כל החבורות הנ"ל, זוהי חבורה מסוימת. החבורה הזו מכילה את כל האיברים שנמצאים בלפחות אחת מן הקבוצות G_n. בפרט, אם איבר כלשהו שייך לG סימן שהוא שייך לאחת החבורות G_n. הבט ברמז ליד התרגיל. --[[משתמש:ארז שיינר|ארז שיינר]] 14:55, 28 בנובמבר 2010 (IST) | ||
| + | :: בסימן <math>G=\bigcup_{n}G_n</math> הכוונה היא לאיחוד <math>G=\bigcup_{n=1}^{\infty}G_n</math>. [[משתמש:עוזי ו.|עוזי ו.]] 22:11, 30 בנובמבר 2010 (IST) | ||
| + | * לקבוצה של מיכאל פרידמן ביום רביעי ב-16-18 מתבטל השיעור בגלל חנוכה, אז למתי צריך להגיש את תרגיל 5? | ||
| + | :: יש להגיש אותו לתא שלי (60) ביום ד הזה (1.12) עד 16:00. תודה, מיכאל. | ||
| + | |||
| + | == תרגיל 7 == | ||
| + | === שאלה 5 === | ||
| + | * מההקשר אני מבין שהכוונה היא למֶרְכָּז ולא למְרַכֵּז (כי אז זה עבור איבר מסויים), אבל אני רוצה לוודא. הבנתי נכון? | ||
| + | :נכון. [[משתמש:דורון פרלמן|דורון פרלמן]] 23:22, 11 בדצמבר 2010 (IST) | ||
| + | |||
| + | == תרגיל 8 == | ||
| + | === שאלה 6 === | ||
| + | * מה זה אומר ש-x,y,z בתוך סוגריים <>? ששלושתם יוצרים? | ||
| + | * x, y, z מייצגים מטריצות מעל Z5? ~~ | ||
| + | |||
| + | |||
| + | -- כן, x,y,z הם יוצרים של החבורה. עתה, חבורת המטריצות <math>G</math> איזומורפית ל(רק) אחת מהשתיים שרשומות שם. לכן x,y,z אינם (מייצגים) מטריצות מעל <math>Z_5</math> אלא שניתן לבנות איזומורפיזם מ- | ||
| + | <math>G</math> לחבורה הנוצרת ע"י x,y,z כך שכל מטריצה תעבור ל-x,y,z (או למכפלות שלהם). | ||
| + | |||
| + | שים לב - הרעיון העומד בבסיס התשובה הוא שהחבורה <math>Z_n</math> והחבורה <math><x : x^n=1></math> איזומורפיות (שלח את היוצר של <math>Z_n</math> (למשל 1) ל- <math>x</math>), אבל אינך יכול לומר ש-<math>x</math> הוא מספר בין 0 ל-<math>n-1</math> (מיכאל פרידמן). | ||
| + | |||
| + | |||
| + | == תרגיל 9 == | ||
| + | * אפשר בבקשה להעלות פתרונות לתרגילים 9-10, ככה שנספיק לעבור עליהם לפני המבחן? תודה! | ||
| + | |||
| + | == פתרונות לחוברת התרגילים == | ||
| + | |||
| + | שלום פרופ' וישנה | ||
| + | תוכל בבקשה לפרסם את קובץ הפתרונות של ספר התרגילים שכתבת בעבורינו. זה יעזור מאוד לקראת הבחינה... | ||
| + | תודה | ||
| + | : אין לי פתרונות כתובים שלא פרסמתי, ואני לא חושב שאספיק לפתור 1200 שאלות עד מחר. אני יכול לפתור שאלות שיצטטו כאן, במספר סביר. [[משתמש:עוזי ו.|עוזי ו.]] 20:33, 23 בינואר 2011 (IST) | ||
גרסה אחרונה מ־21:07, 22 בפברואר 2011
תוכן עניינים
הנחיות
ראשית, קיראו את ההנחיות בעמוד הראשי. דף זה מיועד לשאלות בנוגע לתרגילים - כולל קושיות ותהיות מתמטיות, וגם סוגיות טכניות (לפחות עד שנגְלה את אלה לדף אחר). אנא אל תפתחו כותרות ראשיות שלא לצורך. עוזי ו. 19:28, 7 באוקטובר 2010 (IST)
נושאים כלליים
- האם בהרכבת של פעולה בינארית יכול להיות תנאי? לדוגמה:
a, b שייכים ל N
a + b =
1 אם a זוגי
אחרת 2
- בוודאי שהגדרת הפעולה יכולה להיות מסובכת; פעולה בינארית מתאימה ערך לכל זוג סדור. אין שום סיבה לצפות שהפעולה תהיה מורכבת מפעולות מוכרות. עוזי ו. 20:44, 6 בנובמבר 2010 (IST)
- רוצים לכתוב נוסחאות מתמטיות כאן ולא יודעים איך? אתם יכולים להעזר בעורך LaTeX הבא:
http://www.codecogs.com/latex/eqneditor.php
זה גם עוזר ללמוד קצת LaTeX, תוך כדי, אבל לא חייבים להפנים אם לא רוצים. כדי להכניס את הנוסחה שערכתם, בעת עריכת ההודעה לחצו על ה-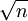 שמופיע ב-toolbar מעל תיבת העריכה והדביקו את הנוסחה במקום הטקסט formula שיופיע.
--84.110.186.131 15:57, 22 בנובמבר 2010 (IST)
שמופיע ב-toolbar מעל תיבת העריכה והדביקו את הנוסחה במקום הטקסט formula שיופיע.
--84.110.186.131 15:57, 22 בנובמבר 2010 (IST)
- במשפט האיזומורפיזם הראשון אמרנו כי לכל הומומורפיזם
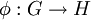 ,
, 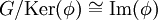 . האם גם הכיוון השני נכון? כלומר, האם זה נכון כי אם
. האם גם הכיוון השני נכון? כלומר, האם זה נכון כי אם 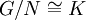 אז קיים אפימורפיזם
אז קיים אפימורפיזם 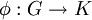 שהגרעין שלו הוא
שהגרעין שלו הוא 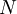 ? --Shwarto 17:56, 5 בדצמבר 2010 (IST)
? --Shwarto 17:56, 5 בדצמבר 2010 (IST)
- בהחלט: ההעתקה
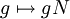 היא אפימורפיזם. עוזי ו. 22:03, 20 בינואר 2011 (IST)
היא אפימורפיזם. עוזי ו. 22:03, 20 בינואר 2011 (IST)
- אז למעשה זה בשני שלבים, לפי מה שאני מבין. קודם מעתיקים לחבורת המנה
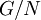 . מכיוון שהיא איזומורפית ל-
. מכיוון שהיא איזומורפית ל-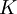 , עפ"י ההנחה, אז קיים איזומורפיזם מ-
, עפ"י ההנחה, אז קיים איזומורפיזם מ-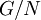 ל-
ל-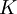 ואז ההרכבה של ההעתקות האלה היא אותו אפימורפיזם
ואז ההרכבה של ההעתקות האלה היא אותו אפימורפיזם 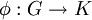 שהגרעין שלו הוא
שהגרעין שלו הוא 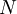 שרציתי לדעת אם הוא קיים. תודה. --Shwarto 17:56, 22 בינואר 2011 (IST)
שרציתי לדעת אם הוא קיים. תודה. --Shwarto 17:56, 22 בינואר 2011 (IST)
- אז למעשה זה בשני שלבים, לפי מה שאני מבין. קודם מעתיקים לחבורת המנה
- בהחלט: ההעתקה
- לגבי תרגיל 7, כתוב למעלה שהקבוצה של יום רביעי (קבוצה 5) צריכה להגיש את התרגיל עד ה-22/12 ואח"כ כתוב שעד 26/12 בשעה 12:00 לתא של מיכאל. מה נכון?
--84.110.207.119 23:22, 19 בדצמבר 2010 (IST)
- יש שתי קבוצות ביום רביעי (04, 05). קבוצה 04 מגישה כרגיל (22/12), קבוצה 05 מגישה עד 26/12. דורון פרלמן 00:57, 20 בדצמבר 2010 (IST)
- כמה תרגילים צריך להגיש סה"כ? תודה.
- 7. דורון פרלמן 21:03, 6 בינואר 2011 (IST)
שאלה על משפט המיון
אפשר לקבל הסבר למשפט הבא: כל חבורת P אבלית איזומורפית למכפלה ישרה של חבורות P ציקליות
- ראשית, יש לדייק: השימוש באות P כדי לסמן מספר ראשוני עלול לבלבל. צריך להיות "כל חבורת-p אבלית איזומורפית למכפלה ישרה של חבורות-p ציקליות". "חבורת-p" (כאשר p הוא מספר ראשוני) היא חבורה שהסדר של כל איבר שלה הוא חזקה של p. לפי משפט קושי, חבורה סופית היא חבורת-p אם ורק אם הסדר שלה הוא חזקה של p בעצמו. בפרט, חבורת-p ציקלית היא חבורה מהצורה
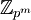 לאיזשהו m.
לאיזשהו m. - אם כך, הטענה היא שכל חבורת-p אבלית איזומורפית למכפלה של חבורות-p ציקליות. מה לא ברור? עוזי ו. 22:01, 20 בינואר 2011 (IST)
- למה יש צורך לציין כי מדובר בחבורת-p אבלית? האם לא כל חבורה שהיא מסדר חזקה של ראשוני היא איזומורפית ל-
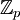 ולכן אבלית?
ולכן אבלית?
- כאשר משתמשים במושג "חבורת-p" הכוונה היא לחבורה שהסדר שלה הוא p^n, ולא כל חבורה מסדר זה היא אבלית (למשל, ראינו חבורות לא אבליות מסדר p^3: מטריצות משולשיות עליונות עם 1 באלכסון ושאר הכניסות ב-
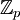 ). מיכאל.
). מיכאל. - יש לך בלבול כלשהו. ננסה לעשות סדר. מה שאנחנו יודעים זה שכל חבורה שהיא מסדר ראשוני היא ציקלית, ושכל חבורה ציקלית מסדר n איזומורפית ל-
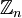 , לכן יש חבורה יחידה מכל סדר p (ראשוני) והיא
, לכן יש חבורה יחידה מכל סדר p (ראשוני) והיא 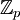 . בנוגע לחזקות של ראשוניים (במקרה הכללי) אנחנו לא יודעים הרבה (כן הוכחנו כמה תוצאות, למשל שהמרכז הוא לא טריוואלי, אבל ממש לא אפיינו את כל החבורות האלה). את/ה שואל/ת "האם לא כל חבורה שהיא מסדר חזקה של ראשוני היא איזומורפית ל-
. בנוגע לחזקות של ראשוניים (במקרה הכללי) אנחנו לא יודעים הרבה (כן הוכחנו כמה תוצאות, למשל שהמרכז הוא לא טריוואלי, אבל ממש לא אפיינו את כל החבורות האלה). את/ה שואל/ת "האם לא כל חבורה שהיא מסדר חזקה של ראשוני היא איזומורפית ל-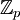 ולכן אבלית"? ודאי שלא! ראשית, איך חבורה שהיא מסדר חזקה של ראשוני יכולה להיות איזומורפית ל-
ולכן אבלית"? ודאי שלא! ראשית, איך חבורה שהיא מסדר חזקה של ראשוני יכולה להיות איזומורפית ל-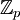 ? למשל איך חבורה מסדר 9 יכולה להיות איזומורפית ל-
? למשל איך חבורה מסדר 9 יכולה להיות איזומורפית ל-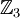 ? באחת יש 9 איברים ובשניה 3 איברים! מעבר לזה, ראינו שיש 5 חבורות מסדר 8 (ו-8 זה 2 בחזקת 3 לכן 8 היא חבורת-p עם p=2), ששתיים מהן לא אבליות (
? באחת יש 9 איברים ובשניה 3 איברים! מעבר לזה, ראינו שיש 5 חבורות מסדר 8 (ו-8 זה 2 בחזקת 3 לכן 8 היא חבורת-p עם p=2), ששתיים מהן לא אבליות (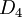 וחבורת הקווטרניונים). לסיכום במקרה הלא אבלי אנחנו לא יודעים הרבה. במקרה האבלי אנחנו יודעים הכל: לפי המשפט שציטטת בראשית דיון זה. דורון פרלמן 19:21, 22 בינואר 2011 (IST)
וחבורת הקווטרניונים). לסיכום במקרה הלא אבלי אנחנו לא יודעים הרבה. במקרה האבלי אנחנו יודעים הכל: לפי המשפט שציטטת בראשית דיון זה. דורון פרלמן 19:21, 22 בינואר 2011 (IST)
- התכוונתי "כל חבורה שהיא מסדר חזקה של ראשוני היא איזומורפית ל-
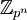 ולכן אבלית", אבל אני מבין כעת שזו שטות גמורה בהנתן דוגמאות פשוטות כמו
ולכן אבלית", אבל אני מבין כעת שזו שטות גמורה בהנתן דוגמאות פשוטות כמו 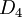 . תודה.--84.110.200.251 18:08, 23 בינואר 2011 (IST)
. תודה.--84.110.200.251 18:08, 23 בינואר 2011 (IST)
- התכוונתי "כל חבורה שהיא מסדר חזקה של ראשוני היא איזומורפית ל-
- כאשר משתמשים במושג "חבורת-p" הכוונה היא לחבורה שהסדר שלה הוא p^n, ולא כל חבורה מסדר זה היא אבלית (למשל, ראינו חבורות לא אבליות מסדר p^3: מטריצות משולשיות עליונות עם 1 באלכסון ושאר הכניסות ב-
- למה יש צורך לציין כי מדובר בחבורת-p אבלית? האם לא כל חבורה שהיא מסדר חזקה של ראשוני היא איזומורפית ל-
שאלה
U32 איזומורפי ל <3>*K. האיבר 3 נבחר כי הוא מסדר האקספוננט, איך בוחרים את התת חבורה הנוספת(את k)?
- ראשית,
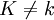 .
. - החבורה שלנו היא חבורת-2 (כלומר, חבורה שסדרה חזקה של 2; במקרה זה 16). מכיוון שהאיבר 3 מסדר השווה לאקספוננט, אפשר להפעיל את המשפט על פירוק של חבורה אבלית G למכפלה ישרה שאחד הגורמים שלה הוא חבורה ציקלית H מסדר האקספוננט (תמצית ההוכחה: בוחרים איבר מסדר p בחבורת המנה G/H, ומחליפים אותו באיבר מסדר p בחבורה G שאינו נמצא ב-H; האיבר הזה יוצר תת-חבורה Q. אחר-כך בונים את הפירוק הישר באינדוקציה בחבורה G/Q, ומרימים הכל ל-G). לחלופין, מכיוון שהסדר של 3 הוא 8, מספיק לבחור איבר מסדר 2 שאינו בתת-החבורה
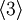 . עוזי ו. 21:01, 22 בינואר 2011 (IST)
. עוזי ו. 21:01, 22 בינואר 2011 (IST)
אוטומורפיזמים
- כאשר יש אוטומורפיזם מחבורה לעצמה שהוא לא הזהות האם בעצם מבחינה רעיונית זה אומר שיש 2 איברים או יותר שמתנהגים אותו הדבר אז אפשר להחליף בינהם?
- חסרה מלת קישור לפני "יש" או "אז". ("אם יש ... אז?", "יש ... ואז"?). תרגיל: מצאו את כל החבורות שבהן יש שני אברים שהחלפתם זה בזה (בלי לשנות אף איבר אחר) היא אוטומורפיזם. עוזי ו. 21:03, 22 בינואר 2011 (IST)
- סליחה על הבלבול התכוונתי עם ו...אז.
- אז אני לא יודע למה הכוונה ב"אפשר להחליף ביניהם". אוטומורפיזם הוא סימטריה של החבורה - ואם הוא מעביר איבר אחד לאיבר אחר (ופועל באותו זמן על כל שאר החבורה, כמובן), זה אומר שאין דרך לזהות ביניהם באמצעות "שאלות חבורתיות"; זו לא חוכמה גדולה, כי האינווריאנט היחיד של איבר בודד הוא הסדר שלו. עוזי ו. 02:04, 23 בינואר 2011 (IST)
קבוצה יוצרת
- אם עושים מתת-קבוצה S של חבורה G לא-אבלית קבוצה יוצרת (כמו שלמדנו) אז למה זה יוצא תת-חבורה? (אם G אבלית אני מבין)
- כל תת-קבוצה (בכל חבורה) יוצרת, בהגדרה, את תת-החבורה הקטנה ביותר המכילה אותה. תת-החבורה הזו כוללת (בדיוק) את כל המכפלות שאפשר להרכיב מן הקבוצה היוצרת (והפכיהם), בכל סדר ובכל אורך שהוא. עוזי ו. 02:06, 23 בינואר 2011 (IST)
תודה, אבל השאלה שלי היא למה יש סגירות לפעולה?
- כי תת-החבורה הנוצרת היא, בהגדרה, תת-החבורה הקטנה ביותר המכילה את הקבוצה. הסבר חלופי: מדובר באוסף כל המכפלות; אם מכפילים שתי מכפלות זו בזו, מתקבלת כמובן מכפלה חדשה (אולי ארוכה יותר). עוזי ו. 20:35, 23 בינואר 2011 (IST)
מאפיין של שדה
- כאשר נתון שדה עם סדר p בחזקת n,אז המאפיין הוא p.האם יוצא מז שכאשר מסתכלים על החבורה החיבורית של השדה,הסדר של כל איבר בשדה הוא p?
- האקספוננט של החבורה החיבורית של שדה שווה למאפיין של השדה. עוזי ו. 00:13, 24 בינואר 2011 (IST)
"מתכון" לאוטומורפיזם
הגדרנו לכל 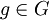 את הפונקציה
את הפונקציה 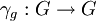 המוגדרת ע"י
המוגדרת ע"י 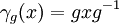 וטענו כי זה אוטומורפיזם. כמו כן, הגדרנו
וטענו כי זה אוטומורפיזם. כמו כן, הגדרנו 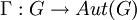 לפי
לפי 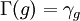 וטענו כי
וטענו כי 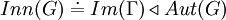 . האם נכון לומר כי הפונקציות
. האם נכון לומר כי הפונקציות 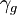 אמנם מגדירות אוטומורפיזמים אך לא בהכרח את כל האוטומורפיזמים ולכן לא בהכרח מתקיים
אמנם מגדירות אוטומורפיזמים אך לא בהכרח את כל האוטומורפיזמים ולכן לא בהכרח מתקיים 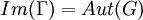 ? כלומר, האופן בו הגדרנו את
? כלומר, האופן בו הגדרנו את 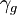 בסה"כ מגדיר לנו אוטומורפיזם אבל זו אינה שיטה לקבל את כל האוטומורפיזמים האפשריים.
אני מבין כי עבור חבורה אבלית זה לא חייב לתת את כל האוטומורפיזמים האפשריים כי לכל
בסה"כ מגדיר לנו אוטומורפיזם אבל זו אינה שיטה לקבל את כל האוטומורפיזמים האפשריים.
אני מבין כי עבור חבורה אבלית זה לא חייב לתת את כל האוטומורפיזמים האפשריים כי לכל 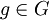 מתקיים
מתקיים 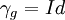 בעוד שאם לחבורה כזו יש יותר מיוצר אחד אז אפשר להעביר כל יוצר לכל יוצר אחר ואז לקבל אוטומורפיזם שונה - כלומר, לא רק את
בעוד שאם לחבורה כזו יש יותר מיוצר אחד אז אפשר להעביר כל יוצר לכל יוצר אחר ואז לקבל אוטומורפיזם שונה - כלומר, לא רק את 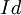 , אבל מה לגבי חבורות לא אבליות?
, אבל מה לגבי חבורות לא אבליות?
- אתה צודק: לא בהכרח שחבורת האוטומורפיזמים הפנימיים תהיה חבורת כל האוטומורפיזמים. בנוסף, אתה יודע שבחבורה לא אבלית,
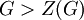 , ולכן חבורת המנה
, ולכן חבורת המנה 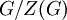 איננה טריוויאלית. אבל חבורה זו איזומורפית לחבורת האוטומור' הפנימיים, ולכן בחבורה לא אבלית תמיד יש אוטומורפיזמים פנימיים. אם אינני טועה, השאלה אם עבור חבורה לא אבלית
איננה טריוויאלית. אבל חבורה זו איזומורפית לחבורת האוטומור' הפנימיים, ולכן בחבורה לא אבלית תמיד יש אוטומורפיזמים פנימיים. אם אינני טועה, השאלה אם עבור חבורה לא אבלית 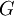 מתקיים
מתקיים 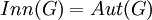 כבר תלויה בחבורה עצמה. למשל,
כבר תלויה בחבורה עצמה. למשל, 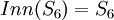 (למה? מהו המרכז של
(למה? מהו המרכז של 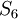 ?) אבל
?) אבל 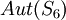 יותר גדולה מחבורת האוטומורפיזמים הפנימיים (זו טענה שקצת יותר קשה להוכיח). מיכאל.
יותר גדולה מחבורת האוטומורפיזמים הפנימיים (זו טענה שקצת יותר קשה להוכיח). מיכאל. - אכן, בדרך כלל יש אוטומורפיזמים לא פנימיים. לגבי "חבורות אבליות עם יותר מיוצר אחד", הדברים שכתבת אינם מדוייקים. לחבורה ציקלית מסדר n יש
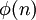 אוטומורפיזמים, אבל המקרה הכללי יותר מורכב. אי אפשר סתם-כך לשלוח "כל יוצר ליוצר אחר". עוזי ו. 13:10, 24 בינואר 2011 (IST)
אוטומורפיזמים, אבל המקרה הכללי יותר מורכב. אי אפשר סתם-כך לשלוח "כל יוצר ליוצר אחר". עוזי ו. 13:10, 24 בינואר 2011 (IST)
- אתה צודק: לא בהכרח שחבורת האוטומורפיזמים הפנימיים תהיה חבורת כל האוטומורפיזמים. בנוסף, אתה יודע שבחבורה לא אבלית,
איך מוכיחים 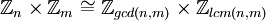
- איך מוכיחים: Zn*Zm איזומורפי ל- Z(n,m)*Zlcm(n,m)?
- זו שאלה לא קלה בכלל. נסמן
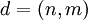 , ונכתוב
, ונכתוב 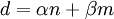 . מתברר ש-
. מתברר ש- 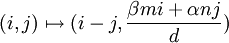 הוא איזומורפיזם
הוא איזומורפיזם 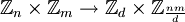 . עוזי ו. 13:35, 24 בינואר 2011 (IST)
. עוזי ו. 13:35, 24 בינואר 2011 (IST)
- הצלחתי להוכיח מוגדרת היטב וחח"ע אבל לא הצלחתי להוכיח על... אפשר כיוון להוכחה?
- החבורות בשני האגפים הן מאותו סדר, כך שאם ההעתקה חד-חד-ערכית היא גם על. עוזי ו. 23:06, 22 בפברואר 2011 (IST)
שאלה על מרכזים של תמורות
- באחת ההרצאות בכיתה, ניתנה הדוגמא כי
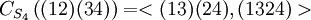 .
.
- הייתי מעוניין לדעת האם יש דרך לדעת את התשובה מבלי לרשום מפורשות את כל איברי S4 ולבדוק, או לחלופין כיצד הגענו לתשובה הזו. תודה.
יש כמה דרכים לחשב את המרכז של תמורה בחבורת הסימטריות. הדרך הקלה ביותר בדרך כלל היא להשתמש בחישוב על הצמדה, שלפיו כדי ש-x יתחלף עם (12)(34), צריך להתקיים השוויון 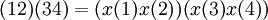 . מכיוון שבשני האגפים מופיעים מחזורים זרים והפירוק למחזורים זרים הוא יחיד, ה"פתרון" למשוואה הזו הוא או
. מכיוון שבשני האגפים מופיעים מחזורים זרים והפירוק למחזורים זרים הוא יחיד, ה"פתרון" למשוואה הזו הוא או 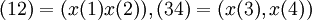 או להיפך; ובכל מקרה יש ארבעה פתרונות ל-x. עוזי ו. 23:04, 22 בפברואר 2011 (IST)
או להיפך; ובכל מקרה יש ארבעה פתרונות ל-x. עוזי ו. 23:04, 22 בפברואר 2011 (IST)
ציון בקורס
האם צריך ציון עובר במבחן ובתרגול בנפרד, או שאם ביחד זה עובר אז זה מספיק (למרות שבמבחן הציון פחות מ-60)?
- הציון הקובע הוא הממוצע המשוקלל. עוזי ו. 23:04, 22 בפברואר 2011 (IST)
תרגיל 1
תרגיל 2
שאלה 2
מהו X, הכוונה לכל X. X שייך לB,
X שייך לR??
-- ניתן לחשוב על X כעל משתנה (כמו בפולינומים), ולכן הוא לא שייך ל-R או ל-B. הרעיון
הוא להסתכל על קבוצת כל הביטויים מהצורה 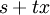 כאשר הכפל (הפעולה) ביניהם מוגדר כפי שהוא מוגדר בשאלה (מיכאל פרידמן).
כאשר הכפל (הפעולה) ביניהם מוגדר כפי שהוא מוגדר בשאלה (מיכאל פרידמן).
שאלה 5
האם בנוסף להנחות בשאלה מותר להניח כי:
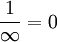 ?
?
-- כן (מיכאל פרידמן)
שאלה 6
כדי להוכיח שהקבוצה היא מונואיד (מלבד סגירות ואבר יחידה) מספיק לומר שהרכבת טרספו' לינאריות היא אסוציאטיבית או שצריך ממש להוכיח את זה? (איך מוכיחים דבר כזה?!)
- העתקות ליניאריות הן פונקציות. הרכבה של פונקציות היא תמיד אסוציאטיבית. עוזי ו. 21:51, 26 באוקטובר 2010 (IST)
שונות
שאלה כללית לגבי תרגיל 2 - כשאני מנסה להוכיח האם קבוצה היא חבורה למחצה, האם עליי להוכיח סגירות ואסוציאטיביות או שמספיק להוכיח רק אסוצ'?
- פורמלית, קבוצה אינה יכולה להיות חבורה למחצה: חבורה למחצה היא מערכת מתמטית הכוללת שני מרכיבים - קבוצה ופעולה בינארית. ופעולה, מעצם טיבה, היא "סגורה". לכן, אם נתונות קבוצה ופעולה, די להוכיח שהפעולה אסוציאטיבית. אם נתונות קבוצה ו"הצעה לפעולה", יש לבדוק שהפעולה אכן מוגדרת היטב, ואז שהיא גם אסוציאטיבית.
- לפעמים יש ברקע חבורה למחצה A עם פעולה משלה, ויש לבדוק האם תת-קבוצה B מהווה חבורה למחצה. במקרה כזה הכוונה היא לפעולה המצומצמת מ-A, כלומר לפונקציה המחזירה עבור שני אברים של B את המכפלה שלהם ב-A; א-פריורי, הפונקציה הזו עלולה להחזיר איברים של A שאינם ב-B, ואז היא אינה פעולה. הפונקציה מוגדרת היטב על B אם היא מחזירה ערך ב-B לכל שני אברים של B (כלומר, אם הקבוצה B סגורה ביחס לפעולה). מאידך, את האסוציאטיביות אין צורך לבדוק בנפרד, משום שהיא מתקבלת בירושה מ-A. עוזי ו. 22:26, 31 באוקטובר 2010 (IST)
- לא הבנתי איך אני מבדילה בתרגיל שקיבלנו (למשל בשאלה 1) בין פעולה "נתונה" ל"הצעה לפעולה"? --93.172.3.238 03:00, 1 בנובמבר 2010 (IST)
- יש לבדוק גם סגירות. דורון פרלמן 03:52, 1 בנובמבר 2010 (IST)
- לא כל מה שאומר "אני פעולה" הוא פעולה. לדוגמא, בסעיף ג' של שאלה 1 מבקשים שתוכיחו שהקבוצה
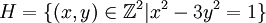 עם ה"פעולה"
עם ה"פעולה" 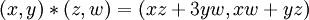 היא חבורה למחצה. הצעד הראשון הוא לבדוק שזו באמת פעולה, כלומר, שהיא מחזירה איברים של H (ולא סתם זוגות סדורים). זו הסגירות המפורסמת. (ואכן, מה אם היו מבקשים לבדוק ש-H חבורה למחצה "תחת פעולת חיבור הוקטורים"?) אחריה, המועמד-לפעולה מקבל קידום ונעשה פעולה לכל דבר ועניין (ואז יש לבדוק שהיא אסוציאטיבית). עוזי ו. 11:37, 1 בנובמבר 2010 (IST)
היא חבורה למחצה. הצעד הראשון הוא לבדוק שזו באמת פעולה, כלומר, שהיא מחזירה איברים של H (ולא סתם זוגות סדורים). זו הסגירות המפורסמת. (ואכן, מה אם היו מבקשים לבדוק ש-H חבורה למחצה "תחת פעולת חיבור הוקטורים"?) אחריה, המועמד-לפעולה מקבל קידום ונעשה פעולה לכל דבר ועניין (ואז יש לבדוק שהיא אסוציאטיבית). עוזי ו. 11:37, 1 בנובמבר 2010 (IST)
- לא הבנתי איך אני מבדילה בתרגיל שקיבלנו (למשל בשאלה 1) בין פעולה "נתונה" ל"הצעה לפעולה"? --93.172.3.238 03:00, 1 בנובמבר 2010 (IST)
תרגיל 3
- נניח שאני רוצה להגדיר חבורה (*,G). האם מותר לי לבנות את G כ-n-יה כאשר n הוא אינסוף?
80.74.111.178 13:49, 7 בנובמבר 2010 (IST)
- כן. אני מניח שהתכוונת שכל אחד מאיברי G הוא n-יה אינסופית. ל-"n-יה אינסופית" קוראים בדרך כלל "סדרה" (שזו פשוט פונקציה שהתחום שלה הוא
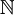 ). בכל אופן אתה יכול להגדיר את G בכל דרך שתרצה, כל עוד הכל מוגדר היטב. דורון פרלמן 17:11, 7 בנובמבר 2010 (IST)
). בכל אופן אתה יכול להגדיר את G בכל דרך שתרצה, כל עוד הכל מוגדר היטב. דורון פרלמן 17:11, 7 בנובמבר 2010 (IST)
- שאלה 4:
מה הכוונה 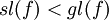 ?
למדנו יחס סדר בין חבורות?
?
למדנו יחס סדר בין חבורות?
- הכוונה היא לאו דווקא ליחס סדר (אם כי אני לא לגמרי בטוח שזה לא מתקיים). כאן, הכוונה בביטוי
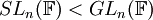 היא ש-
היא ש-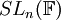 היא תת-חבורה ("ממש") של
היא תת-חבורה ("ממש") של 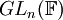 . כלומר,
. כלומר, 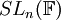 היא חבורה שכל איבריה מוכלים ממש ב-
היא חבורה שכל איבריה מוכלים ממש ב-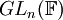 כאשר הפעולה בשתי החבורות היא אותה פעולה. --Shwarto 23:59, 8 בנובמבר 2010 (IST)
כאשר הפעולה בשתי החבורות היא אותה פעולה. --Shwarto 23:59, 8 בנובמבר 2010 (IST)
- הכוונה היא לאו דווקא ליחס סדר (אם כי אני לא לגמרי בטוח שזה לא מתקיים). כאן, הכוונה בביטוי
תרגיל 4
שאלה 1
- בסעיף א, מה הכוונה "חבורת המטריצות ההפיכות כאשר הכניסות הן ב-Z2"? זאת לא אמורה להיות חבורת המטריצות ההפיכות מגודל 2*2 מעל Z2?
ומעל איזו פעולה מדובר? 93.172.153.180 15:28, 22 בנובמבר 2010 (IST)
- הכוונה היא שאיברי המטריצה הם ב-
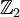 . הפעולה היא כפל מטריצות. --84.110.186.131 15:46, 22 בנובמבר 2010 (IST)
. הפעולה היא כפל מטריצות. --84.110.186.131 15:46, 22 בנובמבר 2010 (IST)
- הכוונה היא שאיברי המטריצה הם ב-
תרגיל 5
- בשאלה 2 סעיף ב לא מנוסח באופן חד משמעי, האם הכוונה שלחבורה G אין תת חבורות נוספות כלל פרט לH? (הרי יש לפחות את הטריוויאליות). האם הכוונה שמסדר n אין עוד ת"ח לG פרט לH? מי הוא n? האם ניתן להניח כי
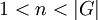 ? אולי הכוונה בכלל ש
? אולי הכוונה בכלל ש 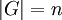 ? (ואז אין בעצם כל כך מה להוכיח). אשמח להבהרות שיסבירו באופן חד משמעי מה השאלה פה.
? (ואז אין בעצם כל כך מה להוכיח). אשמח להבהרות שיסבירו באופן חד משמעי מה השאלה פה.
- ניסוח יותר טוב: הוסף בתחילת הסעיף "יהי n ב-
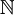 ". (ובמילים אחרות: אתה צריך להראות שאם יש תת-חבורה כך שאין עוד תת-חבורות מאותו הסדר, אז היא נורמלית.) - דורון
". (ובמילים אחרות: אתה צריך להראות שאם יש תת-חבורה כך שאין עוד תת-חבורות מאותו הסדר, אז היא נורמלית.) - דורון
- ניסוח יותר טוב: הוסף בתחילת הסעיף "יהי n ב-
- בשאלה 7 נתון שהחבורות
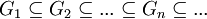 פשוטות ויש להוכיח כי
פשוטות ויש להוכיח כי 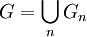 פשוטה. זה הרי נתון שהיא פשוטה, לא? כתוב על כל אחת מהן שהן פשוטות ושהן מוכלות אחת בשניה, אז האיחוד הזה הוא ממילא אותה חבורה עצמה שנתון שהיא פשוטה. לא ברור לי מה יש להוכיח כאן.
פשוטה. זה הרי נתון שהיא פשוטה, לא? כתוב על כל אחת מהן שהן פשוטות ושהן מוכלות אחת בשניה, אז האיחוד הזה הוא ממילא אותה חבורה עצמה שנתון שהיא פשוטה. לא ברור לי מה יש להוכיח כאן.
- לא הבנתי את כוונתך. "האיחוד הזה הוא ממילא אותה חבורה עצמה" - איזו חבורה עצמה? לא נתון כי G פשוטה. אתה צריך להוכיח כי היא פשוטה. דורון פרלמן 19:29, 27 בנובמבר 2010 (IST)
- אם הבנתי נכון, אני צריך להראות שלכל n, האיחוד הנ"ל הוא חבורה פשוטה, אבל נתון שכל
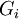 היא פשוטה. מהנתון, גם ברור כי
היא פשוטה. מהנתון, גם ברור כי 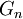 שווה לאיחוד של כל ה-
שווה לאיחוד של כל ה-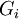 עבור i שקטן מ-n או שווה לו, כי היא מכילה אותם. אז בעצם ברור כי
עבור i שקטן מ-n או שווה לו, כי היא מכילה אותם. אז בעצם ברור כי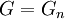 , והרי נתון ש-
, והרי נתון ש-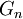 פשוטה, אז לא ברור לי מה יש להוכיח.--84.110.206.83 09:54, 28 בנובמבר 2010 (IST)
פשוטה, אז לא ברור לי מה יש להוכיח.--84.110.206.83 09:54, 28 בנובמבר 2010 (IST)
- עבור איזה n בדיוק מתקיים לדעתך
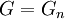 . עבור 10? 100? 1000? הרי כל G_n עשוייה להוסיף איברים חדשים, אין פה שום חבורה אחרונה. --ארז שיינר 12:13, 28 בנובמבר 2010 (IST)
. עבור 10? 100? 1000? הרי כל G_n עשוייה להוסיף איברים חדשים, אין פה שום חבורה אחרונה. --ארז שיינר 12:13, 28 בנובמבר 2010 (IST)
- אז הכוונה היא להוכיח שזה נכון לכל n (וזה עדיין משהו שנתון)? או שעבור
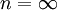 ? שגם זה משהו שלא כ"כ ברור לי.--84.110.206.83 13:31, 28 בנובמבר 2010 (IST)
? שגם זה משהו שלא כ"כ ברור לי.--84.110.206.83 13:31, 28 בנובמבר 2010 (IST)
- יש להוכיח לאיחוד של כל החבורות הנ"ל, זוהי חבורה מסוימת. החבורה הזו מכילה את כל האיברים שנמצאים בלפחות אחת מן הקבוצות G_n. בפרט, אם איבר כלשהו שייך לG סימן שהוא שייך לאחת החבורות G_n. הבט ברמז ליד התרגיל. --ארז שיינר 14:55, 28 בנובמבר 2010 (IST)
- אז הכוונה היא להוכיח שזה נכון לכל n (וזה עדיין משהו שנתון)? או שעבור
- עבור איזה n בדיוק מתקיים לדעתך
- אם הבנתי נכון, אני צריך להראות שלכל n, האיחוד הנ"ל הוא חבורה פשוטה, אבל נתון שכל
- בסימן
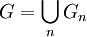 הכוונה היא לאיחוד
הכוונה היא לאיחוד 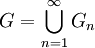 . עוזי ו. 22:11, 30 בנובמבר 2010 (IST)
. עוזי ו. 22:11, 30 בנובמבר 2010 (IST)
- לקבוצה של מיכאל פרידמן ביום רביעי ב-16-18 מתבטל השיעור בגלל חנוכה, אז למתי צריך להגיש את תרגיל 5?
- יש להגיש אותו לתא שלי (60) ביום ד הזה (1.12) עד 16:00. תודה, מיכאל.
תרגיל 7
שאלה 5
- מההקשר אני מבין שהכוונה היא למֶרְכָּז ולא למְרַכֵּז (כי אז זה עבור איבר מסויים), אבל אני רוצה לוודא. הבנתי נכון?
- נכון. דורון פרלמן 23:22, 11 בדצמבר 2010 (IST)
תרגיל 8
שאלה 6
- מה זה אומר ש-x,y,z בתוך סוגריים <>? ששלושתם יוצרים?
- x, y, z מייצגים מטריצות מעל Z5? ~~
-- כן, x,y,z הם יוצרים של החבורה. עתה, חבורת המטריצות 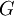 איזומורפית ל(רק) אחת מהשתיים שרשומות שם. לכן x,y,z אינם (מייצגים) מטריצות מעל
איזומורפית ל(רק) אחת מהשתיים שרשומות שם. לכן x,y,z אינם (מייצגים) מטריצות מעל 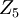 אלא שניתן לבנות איזומורפיזם מ-
אלא שניתן לבנות איזומורפיזם מ-
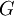 לחבורה הנוצרת ע"י x,y,z כך שכל מטריצה תעבור ל-x,y,z (או למכפלות שלהם).
לחבורה הנוצרת ע"י x,y,z כך שכל מטריצה תעבור ל-x,y,z (או למכפלות שלהם).
שים לב - הרעיון העומד בבסיס התשובה הוא שהחבורה 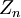 והחבורה
והחבורה 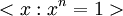 איזומורפיות (שלח את היוצר של
איזומורפיות (שלח את היוצר של 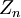 (למשל 1) ל-
(למשל 1) ל-  ), אבל אינך יכול לומר ש-
), אבל אינך יכול לומר ש- הוא מספר בין 0 ל-
הוא מספר בין 0 ל-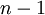 (מיכאל פרידמן).
(מיכאל פרידמן).
תרגיל 9
- אפשר בבקשה להעלות פתרונות לתרגילים 9-10, ככה שנספיק לעבור עליהם לפני המבחן? תודה!
פתרונות לחוברת התרגילים
שלום פרופ' וישנה תוכל בבקשה לפרסם את קובץ הפתרונות של ספר התרגילים שכתבת בעבורינו. זה יעזור מאוד לקראת הבחינה... תודה
- אין לי פתרונות כתובים שלא פרסמתי, ואני לא חושב שאספיק לפתור 1200 שאלות עד מחר. אני יכול לפתור שאלות שיצטטו כאן, במספר סביר. עוזי ו. 20:33, 23 בינואר 2011 (IST)