הבדלים בין גרסאות בדף "אינטגרל לא מסויים/דוגמאות"

גרסה אחרונה מ־22:41, 10 בינואר 2017

תוכן עניינים

1 1
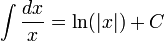
2 2
- 2.1 פתרון
3 3
- 3.1 פתרון
4 4
- 4.1 דרך א'
- 4.2 דרך ב'
5 5
- 5.1 פתרון
6 6
- 6.1 פתרון
7 7
- 7.1 פתרון
8 8
- 8.1 פתרון
9 9
- 9.1 פתרון
10 10
11 11
12 12
- 12.1 פתרון
- 12.2 פתרון (יותר מוצלח כמסתבר)
13 13
- 13.1 פתרון (לא מלא)
14 14
- 14.1 פתרון
15 15
- 15.1 פתרון
16 16
- 16.1 פתרון
17 17

1

$\int\frac{dx}{x}=\ln(|x|)+C$

2

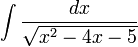
$\int\frac{dx}{\sqrt{x^2-4x-5}}$

פתרון

השלמה לריבוע והצבה ראשונה

הדבר הראשון שנעשה הוא התהליך של השלמה לריבוע, שבסופו נקבל כי:

$x^2-4x-5=(x-2)^2-9$

ולכן ההצבה הראשונה שנעשה תהא: 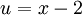$u=x-2$ , וכמובן קל להבין כי $dx=du$ .

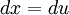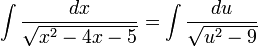
$\int\frac{dx}{\sqrt{x^2-4x-5}}=\int\frac{du}{\sqrt{u^2-9}}$

פונקציות טריגונומטריות היפרבוליות (הערה)

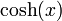ניעזר בתכונות של $\sinh(x)$ ושל $\cosh(x)$ :

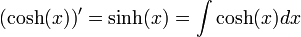
$(\cosh(x))'=\sinh(x)=\int\cosh(x)dx$

וכן בזהות: 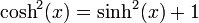$\cosh^2(x)=\sinh^2(x)+1$

הצבה שניה

נציב: 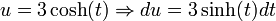$u=3\cosh(t)\Rightarrow du=3\sinh(t)dt$

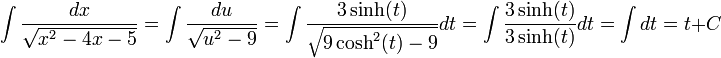
$\int\frac{dx}{\sqrt{x^2-4x-5}}=\int\frac{du}{\sqrt{u^2-9}}=\int\frac{3\sinh(t)}{\sqrt{9\cosh^2(t)-9}}dt=\int\frac{3\sinh(t)}{3\sinh(t)}dt=\int dt=t+C$

ולהחזיר את t ל-x, אני משאיר לכם (:

3

האינטגרל הבא לקוח מספר התרגילים של בועז צבאן (1.24, אם אינני טועה)

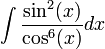
$\int\frac{\sin^2(x)}{\cos^6(x)}dx$

פתרון

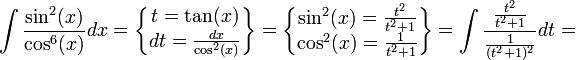
$\int\frac{\sin^2(x)}{\cos^6(x)}dx=\begin{Bmatrix}t=\tan(x)\\ dt=\frac{dx}{\cos^2(x)}\end{Bmatrix}=\begin{Bmatrix}\sin^2(x)=\frac{t^2}{t^2+1}\\ \cos^2(x)=\frac{1}{t^2+1}\end{Bmatrix}=\int\frac{\frac{t^2}{t^2+1}}{\frac{1}{(t^2+1)^2}}dt=$

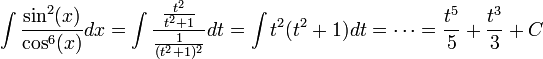
$\int\frac{\sin^2(x)}{\cos^6(x)}dx=\int\frac{\frac{t^2}{t^2+1}}{\frac{1}{(t^2+1)^2}}dt=\int t^2(t^2+1)dt=\cdots=\frac{t^5}{5}+\frac{t^3}{3}+C$

יש טעות בהצבה של

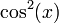\cos^2(x)

, שכן

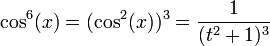
\cos^6(x)=(\cos^2(x))^3=\frac{1}{(t^2+1)^3}

אבל צריך לקחת בחשבון גם את ה-dt

צודק. נראה לי שאם אני לא ראיתי את זה, גם אחרים לא יראו ;)

4

בדומה לאינטגרל הקודם, לקוח מבועז צבאן (1.27)

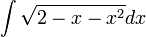
$\int\sqrt{2-x-x^2}dx$

דרך א'

א. ניתן להשתמש בהצבת אוילר, אבל אנחנו ננקוט בטקטיקה שונה.

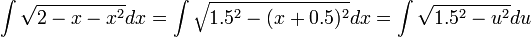
$\int\sqrt{2-x-x^2}dx=\int\sqrt{1.5^2-(x+0.5)^2}dx=\int\sqrt{1.5^2-u^2}du$

הצבה ראשונה: 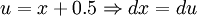$u=x+0.5\Rightarrow dx=du$

הצבה שניה: 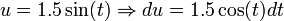$u=1.5\sin(t)\Rightarrow du=1.5\cos(t)dt$

ואם נחזור לחישוב האינטגרל,

$\int\sqrt{1.5^2-u^2}du=\int 1.5\sqrt{1-\sin^2(t)}\cdot1.5\cos(t)dt=2.25\int\cos^2(t)dt=2.25\int\frac{\cos(2t)+1}{2}dt=2.25\left(\frac{\sin(2t)}{4}+\frac{t}{2}\right)+C$

ומכאן מעבירים את t ל-x.

דרך ב'

ההצבה הראשונה נשארת כפי שהייתה, אך הפעם לא נעשה הצבה שניה אלא נשתמש באינטגרציה בחלקים:

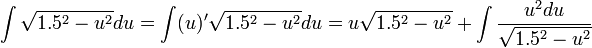
$\int\sqrt{1.5^2-u^2}du=\int (u)'\sqrt{1.5^2-u^2}du=u\sqrt{1.5^2-u^2}+\int\frac{u^2du}{\sqrt{1.5^2-u^2}}$

כעת נוכל להבחין כי מתקיים:

$\int\frac{u^2}{\sqrt{1.5^2-u^2}}du=\int\frac{u^2-1.5^{2}+1.5^2}{\sqrt{1.5^2-u^2}}du=\int\frac{1.5^2}{\sqrt{1.5^2-u^2}}du-\int\sqrt{1.5^2-u^2}du$

כעת נביט רק על האינטגרל הראשון ונציב: 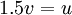$1.5v=u$

$\int\frac{1.5^2}{\sqrt{1.5^2-u^2}}du=1.5^2\int\frac{1.5}{1.5\sqrt{1-v^2}}dv=1.5^2\arcsin(v)=2.25\arcsin\left(\frac{2u}{3}\right)+C$

אם נחזור לאינטגרל המקורי נקבל:

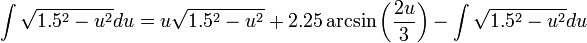
$\int\sqrt{1.5^2-u^2}du=u\sqrt{1.5^2-u^2}+2.25\arcsin\left(\frac{2u}{3}\right)-\int\sqrt{1.5^2-u^2}du$

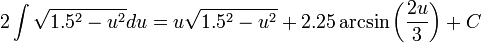
$2\int\sqrt{1.5^2-u^2}du=u\sqrt{1.5^2-u^2}+2.25\arcsin\left(\frac{2u}{3}\right)+C$

וסיימנו (:

5

אינטגרל חביב שנלקח ממבחן בחדו"א בב"ג (של מדעי המחשב)

$\int\frac{dx}{x+\sqrt[n]{x}}$ כאשר $n\in\N$ .

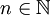פתרון

הכוונה היא עבור 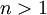$n>1$ , עבור 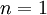$n=1$ תסתכלו בדוגמא הראשונה.

$\int\frac{dx}{x+\sqrt[n]{x}}=\begin{Bmatrix}t^n=x\\nt^{n-1}dt=dx\end{Bmatrix}=\int\frac{nt^{n-1}}{t^n+t}dt=n\int\frac{t^{n-2}}{t^{n-1}+1}dt=\begin{Bmatrix}k=t^{n-1}+1\\dk=(n-1)t^{n-2}dt\end{Bmatrix}=$

$\int\frac{dx}{x+\sqrt[n]{x}}=\frac{n}{n-1}\int\frac{dk}{k}=\frac{n}{n-1}\ln(|k|)+c=\frac{n}{n-1}\ln\Big(|x^{\frac{n-1}{n}}+1|\Big)+C$

6

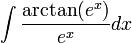
$\int\frac{\arctan(e^x)}{e^x}dx$

פתרון

נעזר באינטגרציה בחלקים.

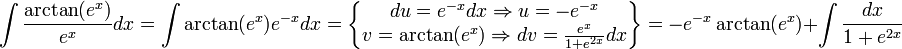
$\int\frac{\arctan(e^{x})}{e^{x}}dx=\int\arctan(e^{x})e^{-x}dx=\begin{Bmatrix}du=e^{-x}dx\Rightarrow u=-e^{-x}\\ v=\arctan(e^{x})\Rightarrow dv=\frac{e^x}{1+e^{2x}}dx\end{Bmatrix}=-e^{-x}\arctan(e^x)+\int\frac{dx}{1+e^{2x}}$

פתאום זה נראה יותר אנושי, כעת נסתכל על האינטגרל שנותר:

$\int\frac{dx}{1+e^{2x}}=\begin{Bmatrix}t=e^{2x}\\dt=2t\,dx\end{Bmatrix}=\int\frac{dt}{2t(1+t)}= \int\frac{dt}{2t}-\int\frac{dt}{2t+2}=0.5\big(\ln(|t|)-\ln(|t+1|)\big)+C=0.5\ln\left(\frac{e^{2x}}{1+e^{2x}}\right)+C$

לבסוף:

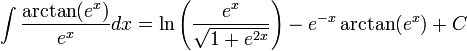
$\int\frac{\arctan(e^x)}{e^x}dx=\ln\left(\frac{e^x}{\sqrt{1+e^{2x}}}\right)-e^{-x}\arctan(e^x)+C$

7

$\int\frac{\sqrt{x^2-16}}{x}dx$

פתרון

נעשה את ההצבה הבאה: 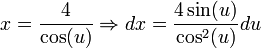$x=\frac{4}{\cos(u)}\Rightarrow dx=\frac{4\sin(u)}{\cos^2(u)}du$

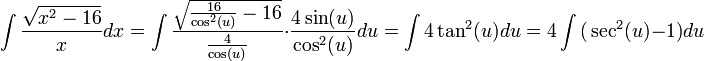
$\int\frac{\sqrt{x^2-16}}{x}dx=\int\frac{\sqrt{\frac{16}{\cos^2(u)}-16}}{\frac{4}{\cos(u)}}\cdot\frac{4\sin(u)}{\cos^2(u)}du= \int 4\tan^2(u)du=4\int\big(\sec^2(u)-1\big)du$

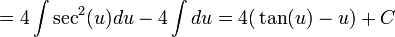
$=4\int\sec^2(u)du-4\int du=4\big(\tan(u)-u\big)+C$

מההצבה הראשונית מתקבל:

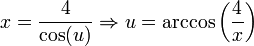
$x=\frac{4}{\cos(u)}\Rightarrow u=\arccos\left(\frac{4}{x}\right)$

לבסוף (אחרי פענוח):

$\int\frac{\sqrt{x^2-16}}{x}dx=\sqrt{x^2-16}-4\arccos\left(\frac{4}{|x|}\right)+C$

8

אחד קליל מהחוברת של בועז (:,

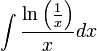
$\int\frac{\ln\left(\frac{1}{x}\right)}{x}dx$

פתרון

נעזר באינטגרציה בחלקים:

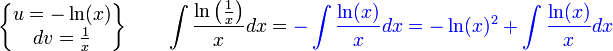
$\begin{Bmatrix}u=-\ln(x)\\dv=\frac{1}{x}\end{Bmatrix}\qquad\int\frac{\ln\left(\frac{1}{x}\right)}{x}dx={\color{blue}-\int\frac{\ln(x)}{x}dx=-\ln(x)^2+\int\frac{\ln(x)}{x}dx}$

קיבלנו:

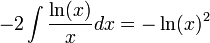
$-2\int\frac{\ln(x)}{x}dx=-\ln(x)^2$

לבסוף:

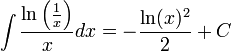
$\int\frac{\ln\left(\frac{1}{x}\right)}{x}dx=-\frac{\ln(x)^2}{2}+C$

9

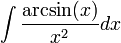
$\int\frac{\arcsin(x)}{x^2}dx$

פתרון

ראשית נפעיל אינטגרציה בחלקים כאשר: 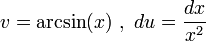$v=\arcsin(x)\ ,\ du=\dfrac{dx}{x^2}$

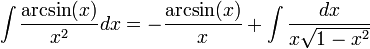
$\int\frac{\arcsin(x)}{x^2}dx=-\frac{\arcsin(x)}{x}+\int\frac{dx}{x\sqrt{1-x^2}}$

כעת נחשב את האינטגרל השני שקיבלנו:

$\int\frac{dx}{x\sqrt{1-x^2}}=\begin{Bmatrix}x=\cos(u)\\dx=\sin(u)du\end{Bmatrix}=\int\dfrac{\sin(u)}{\cos(u)\sqrt{1-\cos^2(u)}}du=\int \frac{du}{\cos(u)}$

וכעת ניעזר בהצבה האוניברסלית כדי למצוא את האינטגרל החדש:

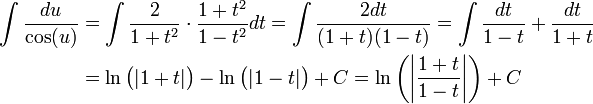
$\begin{align}\int\frac{du}{\cos(u)}&=\int\frac{2}{1+t^2}\cdot\frac{1+t^2}{1-t^2}dt=\int\frac{2dt}{(1+t)(1-t)}=\int\frac{dt}{1-t}+\frac{dt}{1+t}\\&=\ln\big(|1+t|\big)-\ln\big(|1-t|\big)+C=\ln\left(\left|\frac{1+t}{1-t}\right|\right)+C\end{align}$

כרגיל להחזיר ולהנות (:

10

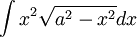
$\int x^2\sqrt{a^2-x^2}dx$

נציב 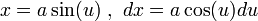$x=a\sin(u)\ ,\ dx=a\cos(u)du$

$\int x^2\sqrt{a^2-x^2}dx=\int a^2\sin^2(u)\sqrt{a^2-a^2\sin^2(u)}a\cos(u)du=a^4\int\big(\sin(u)\cos(u)\big)^2du$

$=\dfrac{a^4}{4}\int\sin^2(2u)du=\dfrac{a^4}{4}\int\frac{1-\cos(4u)}{2}du=\dfrac{a^4}{8}\left(\int du-\int\cos(4u)du\right)=\dfrac{a^4}{8}\left(u-\dfrac{\sin(4u)}{4}\right)+C$

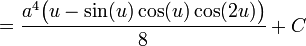
$=\dfrac{a^4\big(u-\sin(u)\cos(u)\cos(2u)\big)}{8}+C$

מההצבה הראשונית מתקבל:

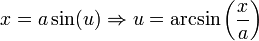
$x=a\sin(u)\Rightarrow u=\arcsin\left(\frac{x}{a}\right)$

לבסוף:

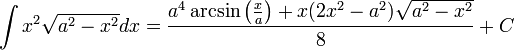
$\int x^2\sqrt{a^2-x^2}dx=\dfrac{a^4\arcsin\left(\frac{x}{a}\right)+x(2x^2-a^2)\sqrt{a^2-x^2}}{8}+C$

11

$\int x^2\sqrt{a^2+x^2}dx$

הצבה היפרבולית $x=a\sinh(u)\ ,\ dx=a\cosh(u)du$

נוסחאות לפונקציות היפרבוליות

12

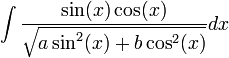
$\int\frac{\sin(x)\cos(x)}{\sqrt{a\sin^2(x)+b\cos^2(x)}}dx$

פתרון

$\int\frac{\sin(x)\cos(x)}{\sqrt{a\sin^2(x)+b\cos^2(x)}}dx=\int\frac{\sin(x)\cos(x)}{\sqrt{(a-b)\sin^2(x)+b}}dx=\begin{Bmatrix}t=\sin(x)\\dt=\cos(x)dx\end{Bmatrix}=\int\frac{t}{\sqrt{(a-b)t^2+b}}dt=\begin{Bmatrix}u=(a-b)t^{2}+b\\ du=2(a-b)tdt\end{Bmatrix}=$

$\frac{1}{2a-2b}\int\frac{du}{\sqrt u}=\frac{\sqrt u}{a-b}+C=\frac{\sqrt{(a-b)t^2+b}}{a-b}+C=\frac{\sqrt{(a-b)\sin^2(x)+b}}{a-b}+C$

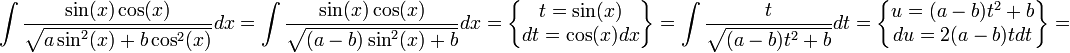
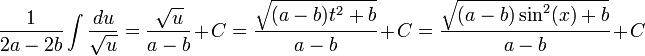
פתרון (יותר מוצלח כמסתבר)

להציב 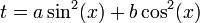$t=a\sin^2(x)+b\cos^2(x)$

13

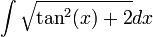
$\int\sqrt{\tan^2(x)+2}dx$

פתרון (לא מלא)

זה לקח לי שני עמודים בכתב יד, זה נורא (אני בטוח שיש פתרון יותר חכם)

הצבה 1: 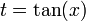$t=\tan(x)$

הצבה 2: 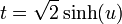$t=\sqrt2\sinh(u)$

אח"כ צריך לשחק עם מה שמקבלים (לפי תכונות של קוסינוס וסינוס היפרבולי), ואז להעביר את זה לייצוג המקורי.

ואז, הצבה 3: $k=e^{2u}$

מכאן זו פונקציה רצינואלית של לינארי חלקי פולינום ממעלה 2, זה לא בעיה בהשוואה למה שהלך למעלה.

במקרה הכי גרוע, תהיה הצבה 4.

14

$\int\frac{dx}{\sqrt[4]{\sin^3(x)\cos^5(x)}}$

פתרון

$\int\frac{dx}{\sqrt[4]{\sin^3(x)\cos^5(x)}}=\int\frac{dx}{\cos(x)\sqrt{\sin(x)}\sqrt[4]{\sin(x)\cos(x)}}=\int\frac{\sqrt{\sin(x)}}{\cos(x)\sin(x)\sqrt[4]{\sin(x)\cos(x)}}dx$

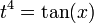
$=2\int\frac{\sqrt[4]{\sin^2(x)}}{\sin(2x)\sqrt[4]{\sin(x)\cos(x)}}dx=2\int\frac{\sqrt[4]{\tan(x)}}{\sin(2x)}dx$

כעת נציב: $t^4=\tan(x)$

$2\int\frac{\sqrt[4]{\tan(x)}}{\sin(2x)}dx=2\int\frac{t}{\frac{2t^4}{t^8+1}}\cdot\frac{4t^3}{(t^8+1)}dt=2\int\frac{4t^4}{2t^4}dt=4\int dt=4\sqrt[4]{\tan(x)}+C$

15

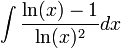
$\int\frac{\ln(x)-1}{\ln(x)^2}dx$

פתרון

(קרדיט מלא לסורקין) תוקן! סורקין לא סרוקין ולא צריך קרדיט...

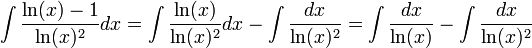
$\int\frac{\ln(x)-1}{\ln(x)^2}dx=\int\frac{\ln(x)}{\ln(x)^2}dx-\int\frac{dx}{\ln(x)^2}=\int\frac{dx}{\ln(x)}-\int\frac{dx}{\ln(x)^2}$

כעת נתמקד באינטגרל הראשון, נפעיל אינטגרציה בחלקים:

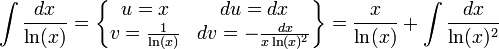
$\int\frac{dx}{\ln(x)}=\begin{Bmatrix}u=x&du=dx\\v=\frac{1}{\ln(x)}&dv=-\frac{dx}{x\ln(x)^2}\end{Bmatrix}=\frac{x}{\ln(x)}+\int\frac{dx}{\ln(x)^2}$

ונשים לב כי מתקיים (באופן די מגניב):

$\int\frac{\ln(x)-1}{\ln(x)^2}dx={\color{blue}\int\frac{dx}{\ln(x)}}-\int\frac{dx}{\ln(x)^2}={\color{blue}\frac{x}{\ln(x)}+\int\frac{dx}{\ln(x)^2}}-\int\frac{dx}{\ln(x)^2}$

לבסוף:

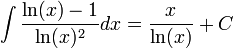
$\int\frac{\ln(x)-1}{\ln(x)^2}dx=\frac{x}{\ln(x)}+C$

16

$\int \frac {\sqrt{1-\sqrt[3]{x}}}{x\cdot \sqrt{1+\sqrt[3]{x}}}dx$

פתרון

הצבה $1-\sqrt[3]{x}=t^2$

לאחר מכן הצבה טריגונומטרית 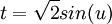$t=\sqrt{2}sin(u)$

ולאחר מכן ההצבה האוניברסאלית של טאנגנס חצי זוית

17

$I_m=\int sin^m(x)dx$

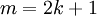אם $m=2k+1$ הינו אי זוגי, אזי:

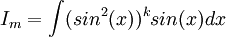
$I_m=\int (sin^2(x))^ksin(x)dx$

נבצע את ההצבה $t=cosx$ לקבל

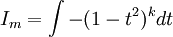$I_m=\int -(1-t^2)^kdt$ וזה פתיר וקל.

כעת, נניח כי 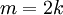$m=2k$ זוגי:

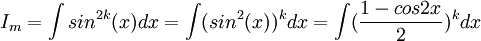
$I_m=\int sin^{2k}(x)dx = \int (sin^2(x))^kdx = \int (\frac{1-cos2x}{2})^k dx$

וזו בעייה במעלה נמוכה יותר של אינטגרל על קוסינוס

אם k אי זוגי אז פותרים באופן דומה להתחלה, ואם לא שוב מקטינים את החזקה על ידי זהות זוית כפולה של קוסינוס.

@@ שורה 169: / שורה 169: @@
 כעת נחשב את האינטגרל השני שקיבלנו:
-<math>\int \frac{dx}{x\sqrt{1-x^{2}}}=\begin{Bmatrix}
+<math>\int\frac{dx}{x\sqrt{1-x^2}}=\begin{Bmatrix}x=\cos(u)\\dx=\sin(u)du\end{Bmatrix}=\int\dfrac{\sin(u)}{\cos(u)\sqrt{1-\cos^2(u)}}du=\int \frac{du}{\cos(u)}</math>
-x=cosu\\
-dx=sinudu
-\end{Bmatrix}=
-\int \frac{sinu}{cosu\sqrt{1-cos^{2}u}}du=\int \frac{du}{cosu}=</math>
 וכעת ניעזר בהצבה האוניברסלית כדי למצוא את האינטגרל החדש:
-<math>\int \frac{du}{cosu}=\int \frac{2}{1+t^{2}}\cdot \frac{1+t^{2}}{1-t^{2}}dt=\int \frac{2dt}{(1+t)(1-t)}=\int\frac{dt}{1-t}+\frac{dt}{1+t}=ln|1+t|-ln|1-t|+c=ln\frac{1+t}{1-t}+c</math>
+<math>\begin{align}\int\frac{du}{\cos(u)}&=\int\frac{2}{1+t^2}\cdot\frac{1+t^2}{1-t^2}dt=\int\frac{2dt}{(1+t)(1-t)}=\int\frac{dt}{1-t}+\frac{dt}{1+t}\\&=\ln\big(|1+t|\big)-\ln\big(|1-t|\big)+C=\ln\left(\left|\frac{1+t}{1-t}\right|\right)+C\end{align}</math>
 כרגיל להחזיר ולהנות (:
@@ שורה 277: / שורה 273: @@
 ונשים לב כי מתקיים (באופן די מגניב):
-<math>\int\frac{\ln(x)-1}{\ln(x)^2}dx=\int\frac{dx}{\ln(x)}-\int\frac{dx}{\ln(x)^2}=\frac{x}{\ln(x)}+C</math>
+<math>\int\frac{\ln(x)-1}{\ln(x)^2}dx={\color{blue}\int\frac{dx}{\ln(x)}}-\int\frac{dx}{\ln(x)^2}={\color{blue}\frac{x}{\ln(x)}+\int\frac{dx}{\ln(x)^2}}-\int\frac{dx}{\ln(x)^2}</math>
+לבסוף:
+<math>\int\frac{\ln(x)-1}{\ln(x)^2}dx=\frac{x}{\ln(x)}+C</math>
 ==16==

הבדלים בין גרסאות בדף "אינטגרל לא מסויים/דוגמאות"

גרסה אחרונה מ־22:41, 10 בינואר 2017

תוכן עניינים

1

2

פתרון

3

פתרון

4

דרך א'

דרך ב'

5

פתרון

6

פתרון

7

פתרון

8

פתרון

9

פתרון

10

11

12

פתרון

פתרון (יותר מוצלח כמסתבר)

13

פתרון (לא מלא)

14

פתרון

15

פתרון

16

פתרון

17

תפריט הניווט

חיפוש