הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/גבול"
יהודה שמחה (שיחה | תרומות) |
(←התכנסות במובן הרחב) |
||
| (2 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 2: | שורה 2: | ||
==גבול של סדרה== | ==גבול של סדרה== | ||
| + | |||
| + | <videoflash>mMVBYUDmSA0</videoflash> | ||
| + | |||
| + | |||
===ההגדרה המדויקת של סדרה=== | ===ההגדרה המדויקת של סדרה=== | ||
<font size=4 color=#3c498e>'''הגדרה.'''</font> | <font size=4 color=#3c498e>'''הגדרה.'''</font> | ||
בבדידה נלמד/למדנו את ההגדרה המדויקת של [[88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 4|פונקציה]]. סדרה הנה פונקציה מקבוצת הטבעיים אל קבוצה כלשהי. סדרה ממשית, למשל, הנה פונקציה מהטבעיים אל הממשיים. | בבדידה נלמד/למדנו את ההגדרה המדויקת של [[88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 4|פונקציה]]. סדרה הנה פונקציה מקבוצת הטבעיים אל קבוצה כלשהי. סדרה ממשית, למשל, הנה פונקציה מהטבעיים אל הממשיים. | ||
| − | באופן טבעי | + | באופן טבעי התמונה של המספר הטבעי 1 נקראת האבר הראשון של הסדרה, התמונה של 2 היא האבר השני וכן הלאה. |
===גבול של סדרה=== | ===גבול של סדרה=== | ||
| שורה 240: | שורה 244: | ||
==התכנסות במובן הרחב== | ==התכנסות במובן הרחב== | ||
| + | |||
| + | <videoflash>U5RUHjrHVGI</videoflash> | ||
| + | |||
| + | |||
דיברנו עד כה על התכנסות סדרה לגבול סופי מסוים. מה לגבי סדרות השואפות לאינסוף? אנו מעוניים להבדיל אותן מסדרות כפי שראינו לעיל שאינן מתקרבות לשום כיוון מסוים. | דיברנו עד כה על התכנסות סדרה לגבול סופי מסוים. מה לגבי סדרות השואפות לאינסוף? אנו מעוניים להבדיל אותן מסדרות כפי שראינו לעיל שאינן מתקרבות לשום כיוון מסוים. | ||
גרסה אחרונה מ־12:43, 20 באוקטובר 2020
תוכן עניינים
גבול של סדרה
ההגדרה המדויקת של סדרה
הגדרה. בבדידה נלמד/למדנו את ההגדרה המדויקת של פונקציה. סדרה הנה פונקציה מקבוצת הטבעיים אל קבוצה כלשהי. סדרה ממשית, למשל, הנה פונקציה מהטבעיים אל הממשיים.
באופן טבעי התמונה של המספר הטבעי 1 נקראת האבר הראשון של הסדרה, התמונה של 2 היא האבר השני וכן הלאה.
גבול של סדרה
תהי סדרת מספרים ממשיים 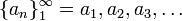 , כך ש-
, כך ש- 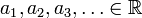 .
.
לדוגמא:
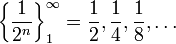
גבול של סדרה הוא נקודה ממשית אליה אברי הסדרה מתקרבים. לסדרה שלא מתקרבת לנקודה ספציפית אין גבול, למשל: 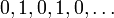 (לסדרה זו אין גבול). נגדיר את מושג הגבול באופן מדויק:
(לסדרה זו אין גבול). נגדיר את מושג הגבול באופן מדויק:
הגדרת הגבול
הגדרה.
תהי  סדרת מספרים ממשיים. אזי מספר ממשי
סדרת מספרים ממשיים. אזי מספר ממשי 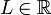 נקרא גבול הסדרה
נקרא גבול הסדרה  אם לכל
אם לכל  קיים
קיים 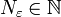 כך שלכל
כך שלכל 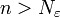 מתקיים
מתקיים 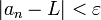 .
.
במקרה זה מסמנים 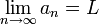 .
.
הסבר ההגדרה
נתרגם את זה למילים. למדנו כי  מודד אורך, מספר טבעי
מודד אורך, מספר טבעי 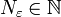 מסמל מקום בסדרה, וערך מוחלט של הפרש מודד מרחק בין שני האברים. בנוסף למדנו על המשפט הלוגי 'לכל סיר יש מכסה שמתאים לו'. עכשיו נרשום את הגדרת הגבול במילים:
מסמל מקום בסדרה, וערך מוחלט של הפרש מודד מרחק בין שני האברים. בנוסף למדנו על המשפט הלוגי 'לכל סיר יש מכסה שמתאים לו'. עכשיו נרשום את הגדרת הגבול במילים:
נקודה 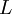 על ציר המספרים הממשיים היא גבול הסדרה
על ציר המספרים הממשיים היא גבול הסדרה 
אם לכל אורך 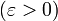 [סיר]
[סיר]
קיים מקום בסדרה 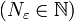 [מכסה]
[מכסה]
כך שהחל ממנו והלאה (לכל 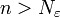 ) מתקיים שהמרחק בין איברי הסדרה והנקודה
) מתקיים שהמרחק בין איברי הסדרה והנקודה 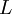 קטן מהאורך
קטן מהאורך 
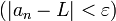 [מתאים לו]
[מתאים לו]
דוגמאות
תרגיל.
מצא את גבול הסדרה 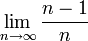
פתרון. מהתבוננות באברים הראשונים של הסדרה אנו מנחשים שגבול הסדרה הנו 1. נוכיח זאת.
יהי  . (הוכחה באינפי מתחילה בשורה זו לעתים תכופות. מכיון שההגדרות דורשות שתכונה מסוימת תתקיים לכל
. (הוכחה באינפי מתחילה בשורה זו לעתים תכופות. מכיון שההגדרות דורשות שתכונה מסוימת תתקיים לכל  , אם נוכיח אותה ל-
, אם נוכיח אותה ל-  מבלי להתייחס לערך שלו, הוכחנו שהיא נכונה תמיד.)
מבלי להתייחס לערך שלו, הוכחנו שהיא נכונה תמיד.)
כעת, אנו רוצים למצוא מקום בסדרה שהחל ממנו והלאה אברי הסדרה קרובים ל-1 עד כדי  . כלומר:
. כלומר:
נפתח את הביטוי.
כעת, אנו מעוניינים כי יתקיים 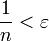 . זה נכון אם"ם
. זה נכון אם"ם 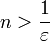 .
.
נבחר, אפוא, 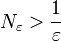 כלשהו (מותר כיון שאחרת המספרים הטבעיים היו חסומים, וידוע שאין חסם עליון למספרים הטבעיים). לכן ברור כי לכל
כלשהו (מותר כיון שאחרת המספרים הטבעיים היו חסומים, וידוע שאין חסם עליון למספרים הטבעיים). לכן ברור כי לכל 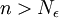 מתקיים
מתקיים 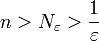 ולכן איברי הסדרה קרובים ל-1 עד כדי
ולכן איברי הסדרה קרובים ל-1 עד כדי  כפי שרצינו.
כפי שרצינו. 
תרגיל.
הוכיחו לפי הגדרה כי מתקיים: 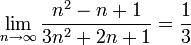
תרגיל.
מצא את גבול הסדרה ![a_n=\sqrt[n]{n}](/images/math/1/1/9/119681e74abf91474f594fb693206280.png)
ננחש את הגבול ע"י הצבה במחשבון (או אינטואיציה מבריקה) להיות 1. כעת, יהי  , נוכיח כי קיים מקום בסדרה החל ממנו אברי הסדרה קרובים ל-1 עד כדי
, נוכיח כי קיים מקום בסדרה החל ממנו אברי הסדרה קרובים ל-1 עד כדי  , כלומר
, כלומר 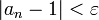 .
.
זה שקול ל- 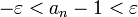
זה שקול ל- ![1-\varepsilon<\sqrt[n]{n}<1+\varepsilon](/images/math/6/1/2/612e734db2223c9b7d047f343a2d27fd.png)
כיון ש- 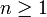 הצד השמאלי טריויאלי (שכן אם השורש היה קטן מאחד, כאשר היינו מעלים אותו בחזקה הוא היה נשאר קטן מאחד). לכן נותר עלינו להוכיח כי קיים מקום בסדרה
הצד השמאלי טריויאלי (שכן אם השורש היה קטן מאחד, כאשר היינו מעלים אותו בחזקה הוא היה נשאר קטן מאחד). לכן נותר עלינו להוכיח כי קיים מקום בסדרה 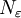 כך שלכל
כך שלכל 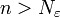 מתקיים
מתקיים ![\sqrt[n]{n}<1+\varepsilon](/images/math/b/3/d/b3da6267d84beb66144ae08edbc5cd03.png)
כלומר, אנו רוצים שיתקיים 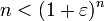
נביט בביטוי 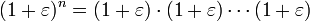 . נזכר בשיעור קומבינטוריקה ונשים לב שכמות האפשרויות לקבל
. נזכר בשיעור קומבינטוריקה ונשים לב שכמות האפשרויות לקבל  כפול
כפול  כפול אחדות בעת פתיחת הסוגריים שווה לכמות האפשרויות לבחור זוגות מבין
כפול אחדות בעת פתיחת הסוגריים שווה לכמות האפשרויות לבחור זוגות מבין  אברים והיא
אברים והיא 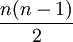 . בסה"כ אנו מקבלים:
. בסה"כ אנו מקבלים:
(כאשר 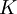 הוא מספר חיובי כלשהו המורכב משאר הכפולות שהשמטנו.)
הוא מספר חיובי כלשהו המורכב משאר הכפולות שהשמטנו.)
אם כך, 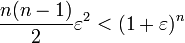 . לכן, אם נמצא מקום בסדרה שהחל ממנו מתקיים
. לכן, אם נמצא מקום בסדרה שהחל ממנו מתקיים 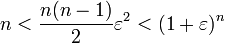 נסיים את התרגיל.
נסיים את התרגיל.
ומכיון שהמספרים הטבעיים אינם חסומים, אחרי מקום מסוים בסדרה אי-השוויון הזה יתקיים כפי שרצינו.
אם כן, הוכחנו כי ![\lim_{n\to\infty}\sqrt[n]{n}=1](/images/math/2/3/0/230b7dcbb77ff9792f922eeaa5b95185.png) .
.

שלילת גבול
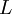 אינו גבול של סדרה אם קיים
אינו גבול של סדרה אם קיים  כך שלכל
כך שלכל 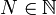 קיים
קיים 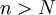 כך ש-
כך ש- 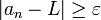 .
.
תרגיל.
הוכח שלסדרה 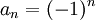 לא קיים גבול.
לא קיים גבול.
נניח בשלילה שקיים גבול 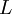 כלשהו. נניח עוד כי
כלשהו. נניח עוד כי 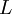 אי-שלילי (ההוכחה עבור השליליים תהא דומה).
אי-שלילי (ההוכחה עבור השליליים תהא דומה).
ניקח 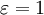 (הרי צריך להוכיח כי קיים
(הרי צריך להוכיח כי קיים  ). כעת, יהי
). כעת, יהי 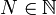 וניקח
וניקח  אי-זוגי גדול ממנו.
אי-זוגי גדול ממנו.
במקרה זה 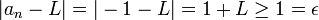 כפי שרצינו. (שימו לב שהורדנו את הערך המוחלט בעזרת ההנחה כי
כפי שרצינו. (שימו לב שהורדנו את הערך המוחלט בעזרת ההנחה כי 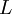 אינו שלילי.)
אינו שלילי.)

אריתמטיקה (חשבון) של גבולות
- משפט
תהיינה 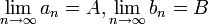 . אזי:
. אזי:
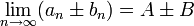
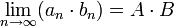
- אם
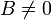 אזי
אזי 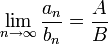
תרגיל.
מצא את גבול הסדרה 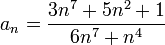 .
.
- פתרון
נחלק את המונה ואת המכנה ב- 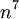 ונקבל
ונקבל 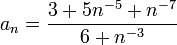 . חזקות שליליות של
. חזקות שליליות של  שואפות ל-0 ולכן לפי אריתמטיקה של גבולות אנו רואים כי הגבול שווה
שואפות ל-0 ולכן לפי אריתמטיקה של גבולות אנו רואים כי הגבול שווה 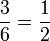 .
.
תרגיל.
נניח 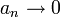 ולסדרה
ולסדרה 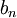 אין גבול. האם אנו יודעים לומר משהו על גבול הסדרה
אין גבול. האם אנו יודעים לומר משהו על גבול הסדרה 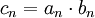 ?
?
תשובה: לא. כל האפשרויות מתקבלות:
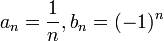 אזי
אזי
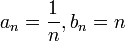 אזי
אזי
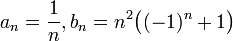 אזי
אזי
![\displaystyle\not\exists\lim_{n\to\infty}(a_n\cdot b_n)=\lim_{n\to\infty}\Big[(-1)^n+1\Big]](/images/math/2/a/7/2a7c140f550c36167ee998b9bcbda556.png) (לא קיים גבול לסדרה זו)
(לא קיים גבול לסדרה זו)
תרגיל חשוב מאד.
תהי סדרה 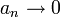 ותהי
ותהי 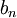 סדרה חסומה. (כלומר, קיים
סדרה חסומה. (כלומר, קיים 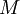 כך שלכל מקום בסדרה
כך שלכל מקום בסדרה  מתקיים
מתקיים 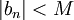 . ישנם אינסוף מספרים בסדרה, אבל קבוצת האברים שנמצאים בסדרה חסומה מלעיל ומלרע).
. ישנם אינסוף מספרים בסדרה, אבל קבוצת האברים שנמצאים בסדרה חסומה מלעיל ומלרע).
הוכח: 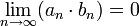
- הוכחה
יהי  , צריך למצוא מקום בסדרה שהחל ממנו והלאה מתקיים
, צריך למצוא מקום בסדרה שהחל ממנו והלאה מתקיים 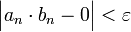 .
.
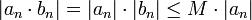 . מכיון שידוע כי הסדרה
. מכיון שידוע כי הסדרה 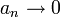 , יש מקום מסוים שהחל ממנו והלאה מתקיים
, יש מקום מסוים שהחל ממנו והלאה מתקיים 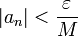 (כיון ש-
(כיון ש- 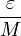 הנו מספר חיובי כלשהו, ולכל מספר חיובי קיים מקום בסדרה עבורו זה מתקיים, לפי הגדרת הגבול).
הנו מספר חיובי כלשהו, ולכל מספר חיובי קיים מקום בסדרה עבורו זה מתקיים, לפי הגדרת הגבול).
לכן, מאותו מקום מתקיים 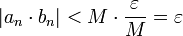 כפי שרצינו.
כפי שרצינו. 
דוגמא.
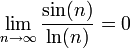
תרגיל.
מצא את הגבול ![\lim\limits_{n\to\infty}\Big[\sqrt{n^2+1}-n\Big]](/images/math/1/6/1/161a5a3f0cb32e78c39362767fd537f6.png)
- פתרון
![\displaystyle\begin{align}\lim_{n\to\infty}\Big[\sqrt{n^2+1}-n\Big]&=\lim_{n\to\infty}\frac{(\sqrt{n^2+1}-n)(\sqrt{n^2+1}+n)}{\sqrt{n^2+1}+n}=\lim_{n\to\infty}\frac{n^2+1-n^2}{\sqrt{n^2+1}+n}\\&=\lim_{n\to\infty}\frac1{\sqrt{n^2+1}+n}\cdot\dfrac{\dfrac1n}{\dfrac1n}=\lim_{n\to\infty}\frac{\dfrac1n}{\dfrac{\sqrt{n^2+1}}{n}+\dfrac{n}{n}}=\lim_{n\to\infty}\frac{\dfrac1n}{\sqrt{1+\dfrac1{n^2}}+1}=0\end{align}](/images/math/b/e/b/bebfd9d4a1b5ee94d951436744626020.png)
אי-שוויון הממוצעים
כלי חשוב לפתרון תרגילים רבים הנו אי-שוויון הממוצעים (אותו לא נוכיח בשלב זה):
לכל  מספרים ממשיים חיוביים
מספרים ממשיים חיוביים 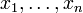 מתקיים:
מתקיים:
![\frac{n}{\frac1{x_1}+\cdots+\frac1{x_n}}\le\sqrt[n]{x_1\times\cdots\times x_n}\le\frac{x_1+\cdots+x_n}{n}](/images/math/d/e/3/de36867c034d59f3ab522014f046b7e7.png)
הביטוי מימין נקרא "ממוצע חשבוני", הביטוי האמצעי נקרא "ממוצע הנדסי" והביטוי השמאלי נקרא "ממוצע הרמוני".
טענה - אתם מוזמנים לנסות להוכיח אותה לבד!
אם 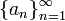 היא סדרת מספרים חיוביים המתכנסת לגבול
היא סדרת מספרים חיוביים המתכנסת לגבול 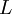 אזי מתקיים:
אזי מתקיים:
![\lim\limits_{n\to\infty}\sqrt[n]{a_1\times\cdots\times a_n}=L](/images/math/6/1/c/61cabfeb83a4fe84dff1ff73672bc82d.png) .
.
- משפט
תהי 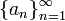 סדרת מספרים חיוביים. אם קיים הגבול
סדרת מספרים חיוביים. אם קיים הגבול 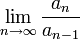 אזי הסדרה
אזי הסדרה
![\big\{\sqrt[n]{a_n}\big\}_{n=1}^\infty](/images/math/a/8/0/a800ca2ef518543a3dd609249d811849.png) מתכנסת ומתקיים השוויון:
מתכנסת ומתקיים השוויון: ![\displaystyle\lim_{n\to\infty}\sqrt[n]{a_n}=\lim_{n\to\infty}\frac{a_n}{a_{n-1}}](/images/math/d/0/0/d0097ed1acf6dc3603ea3c0c4674b82e.png) .
.
- הוכחה
נגדיר סדרה 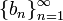 על-ידי
על-ידי 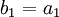 ו-
ו- 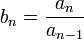 לכל
לכל 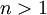 . זוהי סדרת מספרים חיוביים ולכן על-פי הטענה הקודמת מתקיים:
. זוהי סדרת מספרים חיוביים ולכן על-פי הטענה הקודמת מתקיים:
![\displaystyle\lim_{n\to\infty}\sqrt[n]{b_1\times\cdots\times b_n}=\lim_{n\to\infty}b_n=\lim_{n\to\infty}\frac{a_n}{a_{n-1}}](/images/math/7/f/0/7f08c58b0a03ff0f516553298cbf240c.png) .
.
ברור כי
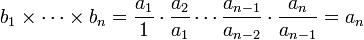
ולכן קיבלנו כי ![\displaystyle\lim_{n\to\infty}\sqrt[n]{a_n}=\lim_{n\to\infty}\frac{a_n}{a_{n-1}}](/images/math/d/0/0/d0097ed1acf6dc3603ea3c0c4674b82e.png) .
. 
כעת נוכיח בדרך אחרת כי ![\lim\limits_{n\to\infty}\sqrt[n]{n}=1](/images/math/6/2/7/6276d61fa92726c9b9c506de5e09123e.png) .
.
- הוכחה
אם נרשום 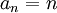 אזי לפי המשפט הקודם מתקיים:
אזי לפי המשפט הקודם מתקיים:
![\displaystyle\lim_{n\to\infty}\sqrt[n]{n}=\lim_{n\to\infty}\sqrt[n]{a_n}=\lim_{n\to\infty}\frac{a_n}{a_{n-1}}=\lim_{n\to\infty}\frac{n}{n-1}=1](/images/math/3/3/9/33968af39590f98fc68b18ad9b21185f.png) .
. 
תרגיל.
תהי סדרה 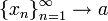 .
.
א. הוכיחו כי אם קיים הגבול 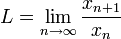 אזי
אזי 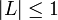 .
.
- פתרון
אם 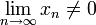 נקבל
נקבל 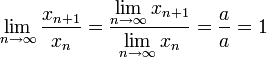 .
.
אחרת, 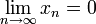 . מאי-שוויון המשולש נקבל
. מאי-שוויון המשולש נקבל 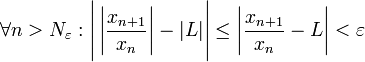 .
.
נובע כי 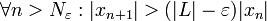 .
.
נניח כעת בשלילה כי 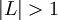 , ניקח
, ניקח 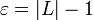 ונקבל כי
ונקבל כי 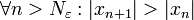
בסתירה לכך ש- 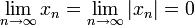 .
. 
ב. תנו דוגמא לסדרה מתכנסת 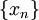 עבורה
עבורה 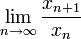 אינו קיים.
אינו קיים.
- פתרון
נתבונן בסדרה 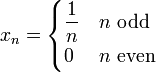
ברור כי 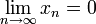 ו-
ו- 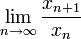 אינו קיים.
אינו קיים.
חוק הסנדוויץ'
הידוע גם בגרסא הרוסית חוק השוטרים והשיכור; לפיו אם שני שוטרים מובילים אדם שיכור ביניהם ושני השוטרים מגיעים לתחנה, אזי גם השיכור (שאינו הולך ישר) יגיע איתם לתחנה. באופן דומה, אם מתקיים 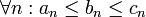 וגם ידוע כי
וגם ידוע כי 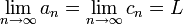 אזי בהכרח
אזי בהכרח 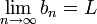 .
.
דוגמא.
מצא את גבול הסדרה 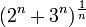
- פתרון
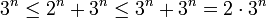
לכן,
כיון שמתקיים
סה"כ שני צדי אי-השוויון מתכנסים ל-3 ואז לפי חוק הסנדוויץ' גם הסדרה שלנו מתכנסת ל-3 .
התכנסות במובן הרחב
דיברנו עד כה על התכנסות סדרה לגבול סופי מסוים. מה לגבי סדרות השואפות לאינסוף? אנו מעוניים להבדיל אותן מסדרות כפי שראינו לעיל שאינן מתקרבות לשום כיוון מסוים.
הגדרה.
תהא  סדרה. אזי אומרים כי הסדרה מתכנסת במובן הרחב לאינסוף אם לכל
סדרה. אזי אומרים כי הסדרה מתכנסת במובן הרחב לאינסוף אם לכל 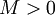 קיים
קיים 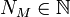 כך שלכל
כך שלכל 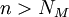 מתקיים
מתקיים 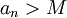 .
.
הערה: שימו לב כי 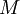 בדומה ל-
בדומה ל-  מודד מרחק, אך מכיון שההגבלה כאן היא חמורה יותר כאשר המרחק גדול (בניגוד לקטן) אנו מסמנים מרחק זה באות
מודד מרחק, אך מכיון שההגבלה כאן היא חמורה יותר כאשר המרחק גדול (בניגוד לקטן) אנו מסמנים מרחק זה באות 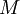 ולא באות
ולא באות  . אנחנו נשמור על מתכונת זו לאורך הקורס.
. אנחנו נשמור על מתכונת זו לאורך הקורס.
ההגדרה להתכנסות במובן הרחב ל- 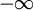 דומה עם שינויים קלים בהתאם.
דומה עם שינויים קלים בהתאם.
תרגיל.
מצא את גבול הסדרה ![a_n=\sqrt[n]{n!}](/images/math/0/0/8/0089796d8bd789eb91640ebfec4adee8.png)
- פתרון
נוכיח כי סדרה זו מתכנסת במובן הרחב לאינסוף.
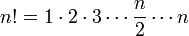 (המקרה בו
(המקרה בו  אינו זוגי מאד דומה אך דורש התעסקות עדינה יותר, לא נפרט לגביו).
אינו זוגי מאד דומה אך דורש התעסקות עדינה יותר, לא נפרט לגביו).
- נקטין את החצי הראשון של האברים להיות 1, ואת החצי השני של האברים להיות
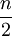 ונקבל:
ונקבל:
ולכן,
קל להוכיח שאם סדרה שואפת לאינסוף, סדרה הגדולה ממנה בכל אבר גם שואפת לאינסוף, כפי שרצינו.
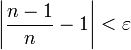
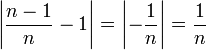
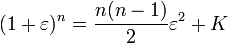
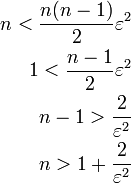
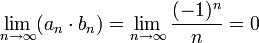
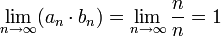
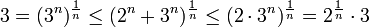
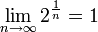
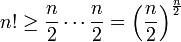
![\sqrt[n]{n!}\ge\sqrt[n]{\left(\dfrac{n}{2}\right)^\frac{n}{2}}=\sqrt{\dfrac{n}{2}}\to\infty](/images/math/a/c/7/ac738fd8a1736bcde1217f776780024a.png)