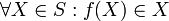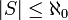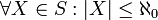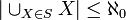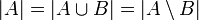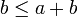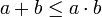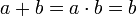הבדלים בין גרסאות בדף "מתמטיקה בדידה - ארז שיינר"
מתוך Math-Wiki
(←משפט קנטור) |
(←חומר עזר) |
||
| (88 גרסאות ביניים של 3 משתמשים אינן מוצגות) | |||
| שורה 2: | שורה 2: | ||
*[[מדיה:16BdidaOrit.pdf|סיכומי ההרצאות של ד״ר ארז שיינר, ע״י אורית חסון, קיץ 2016]] | *[[מדיה:16BdidaOrit.pdf|סיכומי ההרצאות של ד״ר ארז שיינר, ע״י אורית חסון, קיץ 2016]] | ||
*[[מבחנים בבדידה]] | *[[מבחנים בבדידה]] | ||
| + | *[[בחנים בבדידה]] | ||
| + | *[[מבחנים בקורס בדידה למורים]] - שימו לב, הקורס למורים מכיל משמעותית פחות חומר, והמבחנים קלים יותר. יחד עם זאת, יש שם כמות גדולה של תרגילים רלוונטיים ברמה נמוכה. | ||
=סרטוני ותקציר הרצאות= | =סרטוני ותקציר הרצאות= | ||
| + | |||
| + | |||
| + | [https://www.youtube.com/playlist?list=PLHinTfsAOC-vhY2xtz4MJzkm5tefKT3Dg פלייליסט של כל הסרטונים] | ||
| + | |||
==פרק 1 - מבוא ללוגיקה מתמטית== | ==פרק 1 - מבוא ללוגיקה מתמטית== | ||
| + | |||
| + | |||
===פסוקים, קשרים, כמתים, פרדיקטים=== | ===פסוקים, קשרים, כמתים, פרדיקטים=== | ||
| שורה 19: | שורה 27: | ||
===אינדוקציה=== | ===אינדוקציה=== | ||
| + | |||
| + | *משפט האינדוקציה המתמטית | ||
| + | *תהי סדרת טענות כך שמתקיימים שני התנאים הבאים: | ||
| + | **הטענה הראשונה נכונה. | ||
| + | **לכל <math>n\in \mathbb{N}</math> אם הטענה הn מתקיימת אז גם הטענה הn+1 מתקיימת. | ||
| + | *אזי כל הטענות בסדרה נכונות | ||
| + | |||
<videoflash>n6xkPhKmhQo</videoflash> | <videoflash>n6xkPhKmhQo</videoflash> | ||
| + | |||
| + | |||
| + | *דוגמא: | ||
| + | *<math>\sum_{k=1}^{2^{n-1}}\frac{1}{k} > \frac{n}{2}</math> | ||
| + | |||
| + | |||
| + | *אינדוקציה שלמה (מלאה) | ||
| + | *תהי סדרת טענות כך ש: | ||
| + | **לכל <math>n\in \mathbb{N}</math> אם כל הטענות עד ולא כולל הטענה הn מתקיימות, אזי גם הטענה הn מתקיימת. | ||
| + | *אזי כל הטענות בסדרה מתקיימות. | ||
| + | *שימו לב: לפני הטענה הראשונה אין טענות, ולכן כולן מתקיימות באופן ריק. כלומר מנוסח התנאי נובע שצריך להוכיח שהטענה הראשונה מתקיימת. | ||
| + | |||
<videoflash>BBUxvnjuA04</videoflash> | <videoflash>BBUxvnjuA04</videoflash> | ||
| + | |||
| + | |||
| + | *פרדוקס הסוסים (או פתיתי השלג) | ||
| + | |||
<videoflash>E0rf-Cg3IVM</videoflash> | <videoflash>E0rf-Cg3IVM</videoflash> | ||
| שורה 30: | שורה 61: | ||
====תרגול==== | ====תרגול==== | ||
*[[88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 1.5|תרגול בנושא אינדוקציה]] | *[[88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 1.5|תרגול בנושא אינדוקציה]] | ||
| − | *[[מכינה למתמטיקה קיץ תשעב/תרגילים/4|תרגילי אינדוקציה נוספים]] ו[[מכינה למתמטיקה קיץ תשעב/תרגילים/4/פתרון 4| | + | *[[מכינה למתמטיקה קיץ תשעב/תרגילים/4|תרגילי אינדוקציה נוספים]] ו[[מכינה למתמטיקה קיץ תשעב/תרגילים/4/פתרון 4|פתרונותיהם]] |
==פרק 2 - מבוא לתורת הקבוצות== | ==פרק 2 - מבוא לתורת הקבוצות== | ||
===קבוצות ופעולות על קבוצות=== | ===קבוצות ופעולות על קבוצות=== | ||
| + | |||
| + | *איבר שייך לקבוצה <math>a\in A</math> אם הוא אחד האיברים בקבוצה. | ||
| + | *קבוצה מוכלת בקבוצה אחרת <math>A\subseteq B</math> אם <math>\forall a\in A : a\in B</math> | ||
| + | |||
| + | |||
| + | *<math>\{1,2\}=\{2,1\}</math> | ||
| + | *<math>\{1,1,2\}=\{1,2\}</math> | ||
| + | |||
| + | |||
| + | *תהי קבוצה <math>U</math> ותהיינה <math>A,B\subseteq U</math>. נגדיר את: | ||
| + | **קבוצת האיחוד <math>A\cup B =\{ x\in U:x\in A \or x\in B\}</math> | ||
| + | **קבוצת החיתוך <math>A\cap B =\{ x\in U:x\in A \and x\in B\}</math> | ||
| + | **קבוצת ההפרש <math>A\setminus B =\{ x\in U:x\in A \and x\not\in B\}</math> | ||
| + | **קבוצת ההפרש הסימטרי <math>A\Delta B = (A\setminus B)\cup (B\setminus A)</math> | ||
| + | **קבוצת המשלים <math>\overline{A}=\{x\in U:x\not\in A\}</math> | ||
| + | |||
| + | |||
<videoflash>UgNl63BrzCM</videoflash> | <videoflash>UgNl63BrzCM</videoflash> | ||
| שורה 40: | שורה 88: | ||
*[[שיטות הוכחה בסיסיות]] | *[[שיטות הוכחה בסיסיות]] | ||
| + | |||
| + | *הוכחת טענות מכומתות - טענות 'לכל' וטענות 'קיים' | ||
| + | |||
| + | |||
| + | <videoflash>QIwz6eyrcuI</videoflash> | ||
| + | |||
| + | |||
| + | *הוכחת הכלה בין קבוצות, ושיוויון בין קבוצות | ||
| + | |||
| + | |||
| + | <videoflash>Dts0NamGWbE</videoflash> | ||
===איחוד וחיתוך כלליים=== | ===איחוד וחיתוך כלליים=== | ||
| + | |||
| + | *תהי S קבוצה של קבוצות, נגדיר: | ||
| + | **<math>\cup_{A\in S}A = \{x|\exists A\in S :x\in A\}</math> | ||
| + | **<math>\cap_{A\in S}A = \{x|\forall A\in S :x\in A\}</math> | ||
| + | |||
| + | |||
<videoflash>xP9VIaCCH7A</videoflash> | <videoflash>xP9VIaCCH7A</videoflash> | ||
| + | |||
===קבוצת החזקה=== | ===קבוצת החזקה=== | ||
| + | |||
| + | *<math>X\in P(A) \iff X\subseteq A</math> | ||
| + | |||
<videoflash>uZVMvwbs5kw</videoflash> | <videoflash>uZVMvwbs5kw</videoflash> | ||
| שורה 52: | שורה 121: | ||
===מכפלה קרטזית ויחסים=== | ===מכפלה קרטזית ויחסים=== | ||
<videoflash>wyDw5XXmPp8</videoflash> | <videoflash>wyDw5XXmPp8</videoflash> | ||
| + | |||
| + | |||
| + | ====תכונות של יחסים==== | ||
| + | *יהי R יחס על A (כלומר <math>R\subseteq A\times A</math>) אזי: | ||
| + | **R נקרא רפלקסיבי אם לכל <math>a\in A</math> מתקיים <math>aRa</math>. | ||
| + | **R נקרא סימטרי אם לכל <math>a,b\in A</math> המקיימים <math>aRb</math> מתקיים <math>bRa</math> | ||
| + | **R נקרא אנטי-סימטרי אם לכל <math>a,b\in A</math> המקיימים <math>aRb\and bRa</math> מתקיים <math>a=b</math> | ||
| + | **R נקרא טרנזיטיבי אם לכל <math>a,b,c\in A</math> המקיימים <math>aRb \and bRc</math> מתקיים <math>aRc</math> | ||
| + | **R נקרא מלא אם לכל <math>a,b\in A</math> מתקיים כי <math>aRb\or bRa</math> | ||
| + | |||
| + | |||
| + | *יהי R יחס מA לB (כלומר <math>R\subseteq A\times B</math>) אזי: | ||
| + | **R נקרא חד-ערכי (ח"ע) אם לכל <math>a\in A</math> ולכל <math>b_1,b_2\in B</math> המקיימים <math>aRb_1 \and aRb_2</math> מתקיים <math>b_1=b_2</math> | ||
| + | **R נקרא שלם אם לכל <math>a\in A</math> קיים <math>b\in B</math> כך ש <math>aRb</math> | ||
| + | **R נקרא חד-חד-ערכי (חח"ע) אם לכל <math>a_1,a_2\in A</math> ולכל <math>b\in B</math> המקיימים <math>a_1Rb\and a_2Rb</math> מתקיים <math>a_1=a_2</math> | ||
| + | **R נקרא על אם לכל <math>b\in B</math> קיים <math>a\in A</math> כך ש <math>aRb</math> | ||
===יחסי שקילות=== | ===יחסי שקילות=== | ||
| + | *יחס R על קבוצה A נקרא '''יחס שקילות''' אם הוא רפלקסיבי, סימטרי וטרנזיטיבי. | ||
| + | |||
| + | *יהי R יחס שקילות על A. | ||
| + | *לכל <math>a\in A</math> מוגדרת קבוצת '''מחלקת השקילות של a''' ע"י: | ||
| + | **<math>[a]_R=\{x\in A|aRx\}</math> | ||
| + | *קבוצת כל קבוצות מחלקות השקילות נקראת '''קבוצת המנה''': | ||
| + | **<math>A/R=\{[a]_R:a\in A\}</math> | ||
| + | |||
| + | |||
| + | *תהי קבוצה A. קבוצת תתי קבוצות <math>U\subseteq P(A)</math> נקראת '''חלוקה''' של A אם: | ||
| + | **<math>\cup_{X\in U}X=A</math> | ||
| + | **<math>\emptyset\notin U</math> | ||
| + | **לכל <math>X_1,X_2\in U</math> אם <math>X_1\cap X_2\neq \emptyset</math> אזי <math>X_1=X_2</math> | ||
| + | |||
| + | |||
| + | *היחס המושרה מחלוקה: | ||
| + | *תהי קבוצה A ותהי חלוקה שלה U. נגדיר יחס R על A על ידי: | ||
| + | **<math>aRb</math> אם ורק אם קיימת <math>X\in U</math> כך ש<math>a,b\in X</math> | ||
| + | |||
| + | |||
| + | *היחס המושרה מחלוקה הוא יחס שקילות. | ||
| + | *קבוצת המנה היא חלוקה של A. | ||
| + | *היחס המושרה מקבוצת המנה, הוא יחס השקילות המקורי; קבוצת המנה של יחס שקילות מושרה היא החלוקה המקורית. | ||
| + | |||
| + | |||
<videoflash>jKprPSfRysE</videoflash> | <videoflash>jKprPSfRysE</videoflash> | ||
| + | |||
====תרגול==== | ====תרגול==== | ||
| שורה 60: | שורה 171: | ||
===יחסי סדר=== | ===יחסי סדר=== | ||
| + | *יחס R על קבוצה A נקרא '''יחס סדר חלקי''' אם הוא רפלקסיבי, אנטי-סימטרי וטרנזיטיבי | ||
| + | |||
| + | |||
<videoflash>6X0OGf5CJrU</videoflash> | <videoflash>6X0OGf5CJrU</videoflash> | ||
| + | |||
====איברים מינימליים ומקסימליים, וחסמים==== | ====איברים מינימליים ומקסימליים, וחסמים==== | ||
| + | *יהי R יחס סדר חלקי על קבוצה X, ותהי <math>A\subseteq X</math> תת קבוצה. | ||
| + | **איבר <math>M\in A</math> נקרא '''מקסימלי''' בA אם לכל <math>a\in A</math> המקיים <math>MRa</math> מתקיים כי <math>a=M</math> (אין גדולים ממנו) | ||
| + | **איבר <math>m\in A</math> נקרא '''מינימלי''' בA אם לכל <math>a\in A</math> המקיים <math>aRm</math> מתקיים כי <math>a=m</math> (אין קטנים ממנו) | ||
| + | **איבר <math>M\in A</math> נקרא '''הגדול ביותר''' (מקסימום) בA אם לכל <math>a\in A</math> מתקיים <math>aRM</math> (הוא גדול מכולם) | ||
| + | **איבר <math>m\in A</math> נקרא '''הקטן ביותר''' (מינימום) בA אם לכל <math>a\in A</math> מתקיים <math>mRa</math> (הוא קטן מכולם) | ||
| + | **איבר <math>M\in X</math> נקרא '''חסם מלעיל''' של A אם לכל <math>a\in A</math> מתקיים <math>aRM</math> (הוא גדול מכל איברי הקבוצה, אבל לאו דווקא נמצא בקבוצה) | ||
| + | **איבר <math>m\in X</math> נקרא '''חסם מלרע''' של A אם לכל <math>a\in A</math> מתקיים <math>mRa</math> (הוא קטן מכל איברי הקבוצה, אבל לאו דווקא נמצא בקבוצה) | ||
| + | **אם בקבוצת חסמי המלעיל של A יש איבר קטן ביותר הוא נקרא '''חסם עליון''' (supremum) של A. | ||
| + | **אם בקבוצת חסמי המלרע של A יש איבר גדול ביותר הוא נקרא '''חסם תחתון''' (infimum) של A. | ||
| + | |||
| + | |||
| + | *איבר גדול ביותר ביותר הוא יחיד. | ||
| + | *אם חסם מלעיל שייך לקבוצה, אז הוא הגדול ביותר. | ||
| + | *האיבר הגדול ביותר בקבוצה הוא איבר מקסימלי, ואין איברים מקסימליים אחרים. | ||
| + | |||
| + | |||
| + | |||
| + | *האם תתכן קבוצה עם איבר מקסימלי יחיד שאינו האיבר הגדול ביותר בקבוצה? | ||
| + | |||
| + | |||
| + | *ביחס ההכלה על קבוצת חזקה, האיחוד הכללי של קבוצת קבוצות הוא החסם העליון שלה, והחיתוך הכללי הוא החסם התחתון. | ||
| + | *ביחס 'מחלק את' על הטבעיים, המחלק המשותף המקסימלי הוא החסם התחתון, והמכפלה המשותפת המינימלית הוא החסם העליון. | ||
| + | |||
<videoflash>EX6sPaiiu3k</videoflash> | <videoflash>EX6sPaiiu3k</videoflash> | ||
| + | |||
| + | ====שרשראות==== | ||
| + | |||
| + | *יחס סדר חלקי R על A נקרא '''מלא''' (או לינארי, או קווי) אם: | ||
| + | **<math>\forall a,b\in A:aRb\or bRa</math> | ||
| + | |||
| + | |||
| + | *יהי R יחס סדר חלקי על A, ותהי <math>S\subseteq A</math>. | ||
| + | *אזי <math>S</math> נקראת '''שרשרת''' אם היחס מלא עליה, כלומר <math>\forall a,b\in S:aRb\or bRa</math> | ||
====תרגול==== | ====תרגול==== | ||
| שורה 71: | שורה 218: | ||
==פרק 4 - פונקציות== | ==פרק 4 - פונקציות== | ||
===הגדרת פונקציות=== | ===הגדרת פונקציות=== | ||
| + | *יחס f מA לB נקרא פונקציה אם הוא ח"ע ושלם, ומסמנים במקרה זה <math>f:A\to B</math>, וכן <math>f(a)=b\iff (a,b)\in f</math>. | ||
| + | *A נקרא תחום הפונקציה (או תחום הגדרה), B נקרא הטווח של הפונקציה. | ||
| + | |||
| + | |||
| + | *שימו לב, הסרטון ישן, ושם פונקציה הוגדרה כיחס ח"ע בלבד, בניגוד להגדרה העדכנית שלנו בקורס. | ||
| + | |||
| + | |||
<videoflash>XP-SwmSlTUc</videoflash> | <videoflash>XP-SwmSlTUc</videoflash> | ||
===חח"ע ועל, תמונה ותמונה הפוכה=== | ===חח"ע ועל, תמונה ותמונה הפוכה=== | ||
| + | *תהי <math>f:A\to B</math> פונקציה. אזי: | ||
| + | **f חח"ע אם לכל <math>x_1,x_2\in A</math> המקיימים <math>f(x_1)=f(x_2)</math> מתקיים כי <math>x_1=x_2</math> | ||
| + | **f על אם לכל <math>y\in B</math> קיים <math>x\in A</math> כך ש<math>f(x)=y</math> | ||
| + | **תהי <math>X\subseteq A</math> נגדיר את קבוצת התמונה <math>f[X]=\{f(a)|a\in X\}</math> | ||
| + | **תהי <math>Y\subseteq B</math> נגדיר את קבוצת התמונה ההפוכה <math>f^{-1}[Y]=\{a\in A|f(a)\in Y\}</math> | ||
| + | **<math>f[]:P(A)\to P(B)</math> היא פונקצית התמונה, השולחת כל תת קבוצה לקבוצת התמונה שלה | ||
| + | **<math>f^{-1}[]:P(B)\to P(A)</math> היא פונקצית התמונה ההפוכה, השולחת כל תת קבוצה לקבוצת התמונה ההפוכה שלה | ||
| + | |||
| + | |||
| + | *שימו לב | ||
| + | **<math>x\in f^{-1}[Y]\iff f(x)\in Y</math> | ||
| + | **<math>y\in f[X] \iff \exist a\in X :f(a)=y </math> | ||
| + | |||
| + | |||
<videoflash>BgCrOeJEjDo</videoflash> | <videoflash>BgCrOeJEjDo</videoflash> | ||
===הרכבת פונקציות, פונקציות הפיכות=== | ===הרכבת פונקציות, פונקציות הפיכות=== | ||
| + | |||
| + | *תהיינה <math>f:A\to B</math> וכן <math>g:B\to C</math> אזי נגדיר את פונקצית ההרכבה <math>g\circ f:A\to C</math> ע"י <math>g\circ f(a)=g(f(a))</math> | ||
| + | *פעולת ההרכבה היא אסוציאטיבית. | ||
| + | |||
| + | |||
| + | *תהי קבוצה A נגדיר את '''פונקצית הזהות''' <math>I_A:A\to A</math> ע"י <math>I_A(x)=x</math>. | ||
| + | *לכל פונקציה <math>f:A\to B</math> מתקיים כי <math>I_B\circ f = f\circ I_A = f</math> | ||
| + | |||
| + | |||
| + | *פונקציה <math>f:A\to B</math> נקראת הפיכה אם קיימות פונקציות <math>g,h:B\to A</math> כך ש: | ||
| + | **<math>g\circ f = I_A</math> וכן <math>f\circ h = I_B</math> | ||
| + | *נשים לב כי | ||
| + | **<math>h=I_A\circ h = (g\circ f)\circ h = g\circ (f\circ h)=g\circ I_B = g</math> | ||
| + | *לכן אם פונקציה הפיכה, יש פונקציה יחידה שהופכת אותה (ההופכית), נסמנה <math>f^{-1}:B\to A</math>. | ||
| + | *שימו לב: עם סוגריים מרובעים זו פונקצית התמונה ההפוכה שיש לכל פונקציה ופועלת על תתי קבוצות, עם סוגריים עגולים זו הפונקציה ההופכית שיש רק להפיכות ופועלת על איברים. | ||
| + | |||
<videoflash>t5QyDk-Mo2g</videoflash> | <videoflash>t5QyDk-Mo2g</videoflash> | ||
| שורה 97: | שורה 281: | ||
===השוואת עוצמות=== | ===השוואת עוצמות=== | ||
| + | |||
| + | *A שקולת עוצמה לB או עוצמתה של A שווה לB, אם קיימת פונקציה הפיכה (חח"ע ועל) <math>f:A\to B</math>. | ||
| + | *במקרה זה מסמנים <math>A\sim B</math> או <math>|A|=|B|</math>. | ||
| + | **כל קבוצה שקולת עוצמה לעצמה | ||
| + | **אם A שקולת עוצמה לB, גם B שקולת עוצמה לA | ||
| + | **אם A שקולת עוצמה לB וB שקולת עוצמה לC אזי A שקולת עוצמה לC | ||
| + | |||
| + | |||
| + | *עוצמתה של A קטנה או שווה לזו של B, אם קיימת פונקציה חח"ע <math>f:A\to B</math>. | ||
| + | *במקרה זה מסמנים <math>|A|\leq |B|</math> | ||
| + | |||
| + | |||
| + | *כל קבוצה A השקולת עוצמה לקבוצת הטבעיים מסומנת <math>|A|=\aleph_0</math> | ||
| + | |||
| + | *כל קבוצה A השקולת עוצמה לקבוצת הממשיים מסומנת <math>|A|=\aleph</math> | ||
| + | |||
<videoflash>Zu0tX3VcZbg</videoflash> | <videoflash>Zu0tX3VcZbg</videoflash> | ||
| שורה 104: | שורה 304: | ||
<videoflash>H4IwZiUCUvM</videoflash> | <videoflash>H4IwZiUCUvM</videoflash> | ||
| − | ===משפט קנטור-שרדר- | + | ===קבוצות בנות מנייה=== |
| + | *קבוצה A נקראת בת מנייה אם <math>|A|\leq \aleph_0</math> | ||
| + | |||
| + | *כל קבוצה A בת מנייה אינסופית מקיימת <math>|A|=\aleph_0</math> | ||
| + | |||
| + | <videoflash>7TyjNpInOsc</videoflash> | ||
| + | |||
| + | ===חשבון עוצמות (אריתמטיקה של עוצמות)=== | ||
| + | |||
| + | ====חיבור עוצמות==== | ||
| + | *תהיינה שתי עוצמות a,b ותהיינה שתי נציגות זרות לעוצמות A,B. | ||
| + | *נגדיר <math>a+b=|A\cup B|</math>, הגדרה זו אינה תלוייה בבחירת הנציגות. | ||
| + | |||
| + | |||
| + | <videoflash>eDpiO50cDmI</videoflash> | ||
| + | |||
| + | ====כפל עוצמות==== | ||
| + | *תהיינה שתי עוצמות a,b ותהיינה שתי נציגות לעוצמות A,B. | ||
| + | *נגדיר <math>a\cdot b=|A\times B|</math>, הגדרה זו אינה תלוייה בבחירת הנציגות. | ||
| + | |||
| + | |||
| + | <videoflash>AQNIw1ys8B4</videoflash> | ||
| + | |||
| + | ====חזקת עוצמות==== | ||
| + | |||
| + | *תהיינה שתי עוצמות a,b ותהיינה שתי נציגות לעוצמות A,B. | ||
| + | *נגדיר את <math>A^B</math> להיות אוסף כל הפונקציות מB לA (מהמעריך לבסיס). | ||
| + | *נגדיר <math>a^b=|A^B|</math>, הגדרה זו אינה תלוייה בבחירת הנציגות. | ||
| + | |||
| + | |||
| + | <videoflash>aBV5Vt1eMG4</videoflash> | ||
| + | |||
| + | *חוקי חזקות | ||
| + | *תהיינה עוצמות a,b,c אזי | ||
| + | **<math>a^b\cdot a^c = a^{b+c}</math> | ||
| + | **<math>(a^b)^c = a^{b\cdot c}</math> | ||
| + | **<math>a^b\cdot c^b = (a\cdot c)^b</math> | ||
| + | |||
| + | |||
| + | <videoflash>KUTIHDhwjsE</videoflash> | ||
| + | |||
| + | |||
| + | ====עוצמת קבוצת החזקה==== | ||
| + | |||
| + | *<math>|P(A)|=2^{|A|}</math> | ||
| + | |||
| + | |||
| + | <videoflash>pPG6BgSY_Wg</videoflash> | ||
| + | |||
| + | ====השוואת חשבון עוצמות==== | ||
| + | *תהיינה עוצמות a,b,c,d כך ש <math>a\leq c</math> וכן <math>b\leq d</math> אזי: | ||
| + | **<math>a+b\leq c+d</math> | ||
| + | **<math>a\cdot b\leq c\cdot d</math> | ||
| + | *אם בנוסף נתון כי <math>c\neq 0</math> אזי | ||
| + | **<math>a^b\leq c^d</math> | ||
| + | |||
| + | <videoflash>i07f9wwcjtU</videoflash> | ||
| + | |||
| + | ===משפט קנטור-שרדר-ברנשטיין=== | ||
*אם <math>|A|\leq |B|</math> וגם <math>|B|\leq |A|</math> אזי <math>A\sim B</math> | *אם <math>|A|\leq |B|</math> וגם <math>|B|\leq |A|</math> אזי <math>A\sim B</math> | ||
====למת נקודת השבת==== | ====למת נקודת השבת==== | ||
| שורה 112: | שורה 370: | ||
====הוכחת המשפט==== | ====הוכחת המשפט==== | ||
<videoflash>KlZHXHxkzJk</videoflash> | <videoflash>KlZHXHxkzJk</videoflash> | ||
| − | === | + | |
| − | * | + | |
| − | * | + | ====עוצמות קטעים ממשיים==== |
| − | *קבוצות בנות מנייה, | + | |
| − | * | + | *<math>|\mathbb{R}|=|[a,\infty)|=|[a,b]|=|(a,b)|=\aleph</math> |
| − | * | + | |
| − | * | + | |
| − | *כל קבוצה אינסופית | + | <videoflash>qDGHoXKOpzk</videoflash> |
| − | * | + | |
| − | **סכום עוצמות | + | |
| − | * | + | |
| − | ** | + | ===אקסיומת הבחירה ועקרון המקסימום של האוסדורף=== |
| − | ** | + | ====אקסיומת הבחירה==== |
| − | * | + | *תהי S קבוצת קבוצות לא ריקות, ונסמן את האיחוד הכללי ב <math>U=\cup_{X\in S}X</math>. |
| − | *סכום | + | *אזי קיימת פונקצית בחירה <math>f:S\to U</math> הבוחרת איבר מתוך כל קבוצה, כלומר: |
| − | * | + | **<math>\forall X\in S: f(X)\in X</math> |
| + | |||
| + | |||
| + | *דוגמא: | ||
| + | **תהי פונקציה על <math>f:A\to B</math> אזי קיימת תת קבוצה <math>X\subseteq A</math> כך ש <math>f:X\to B</math> חח"ע ועל. | ||
| + | |||
| + | |||
| + | <videoflash>q2OP1NCWKHU</videoflash> | ||
| + | |||
| + | *תהיינה <math>A,B\neq\emptyset</math> אזי <math>|A|\leq |B|</math> אם ורק אם קיימת <math>g:B\to A</math> על. | ||
| + | |||
| + | |||
| + | *בכיוון ראשון: | ||
| + | **תהי <math>f:A\to B</math> חח"ע | ||
| + | **כיוון ש<math>A\neq \emptyset</math> קיים <math>a\in A</math> | ||
| + | **נגדיר פונקציה <math>g:B\to A</math> באופן הבא: | ||
| + | ***לכל <math>b\in B</math> | ||
| + | ***אם קיים <math>x\in A</math> כך ש <math>f(x)=b</math> נגדיר <math>f(b)=x</math> (בגלל החח"ע זה מוגדר היטב) | ||
| + | ***אם <math>b\not\in Im(f)</math> נגדיר <math>f(b)=a</math> | ||
| + | **הפונקציה <math>g</math> שהגדרנו היא אכן על, כי לכל <math>x\in A</math> מתקיים כי <math>g(f(x))=x</math> | ||
| + | *בכיוון שני: | ||
| + | **תהי <math>g:B\to A</math> על, אזי כל הקבוצות באוסף <math>U=\left\{g^{-1}[\{a\}]|a\in A\right\}</math> אינן ריקות. | ||
| + | **ניקח פונקצית בחירה <math>h:U\to B</math> ונגדיר <math>f:A\to B</math> ע"י <math>f(a)=h(g^{-1}[\{a\}])</math> | ||
| + | **אכן <math>f</math> חח"ע כי אם <math>f(a_1)=f(a_2)=b</math> אזי <math>b\in g^{-1}[\{a_1\}]</math> וכן <math>b\in g^{-1}[\{a_2\}]</math> | ||
| + | **ולכן <math>g(b)=a_1</math> וכן <math>g(b)=a_2</math>, כלומר <math>a_1=a_2</math> | ||
| + | |||
| + | |||
| + | <videoflash>Dl6sgVGZksk</videoflash> | ||
| + | |||
| + | ====עקרון המקסימום של האוסדורף==== | ||
| + | *תהי קבוצה A עם יחס סדר חלקי, תת קבוצה <math>S\subseteq A</math> נקראת שרשרת אם היחס מלא עליה (ניתן להשוות בין כל שני איברים בS). | ||
| + | *שרשרת נקראת מקסימלית בA אם היא אינה מוכלת באף שרשרת אחרת. | ||
| + | *עקרון המקסימום של האוסדורף אומר שכל שרשרת מוכלת בשרשרת מקסימלית. | ||
| + | |||
| + | |||
| + | *דוגמא - אוסף עיגולים במישור שאינם חותכים זה את זה, ולא ניתן להוסיף אפילו עיגול אחד נוסף. | ||
| + | |||
| + | |||
| + | <videoflash>O_uDtoDRRZ8</videoflash> | ||
| + | |||
| + | |||
| + | *טענות שימושיות להמשך: | ||
| + | *תהי <math>U</math> קבוצה של יחסים מ<math>A</math> ל <math>B</math>, תהי <math>M\subseteq U</math> שרשרת ביחס ההכלה ונסמן את האיחוד הכללי של השרשרת ב<math>f=\cup_{R\in M} R</math> | ||
| + | *אזי: | ||
| + | **אם כל היחסים ב<math>M</math> ח"ע, אז גם <math>f</math> ח"ע | ||
| + | ***אכן, יהיו <math>(a,b_1),(a,b_2)\in f</math> | ||
| + | ***לכן קיימים <math>R_1,R_2\in M</math> כך ש <math>(a,b_1)\in R_1</math> וכן <math>(a,b_2)\in R_2</math> | ||
| + | ***כיוון ש<math>M</math> שרשרת, אזי <math>R_1\subseteq R_2</math> (או ההפך) ולכן <math>(a,b_1),(a,b_2)\in R_2</math> | ||
| + | ***כיוון ש<math>R_2</math> ח"ע נובע כי <math>b_1=b_2</math> כפי שרצינו. | ||
| + | **אם כל היחסים ב<math>M</math> חח"ע, אזי גם <math>f</math> חח"ע | ||
| + | ***הוכחה דומה לח"ע | ||
| + | |||
| + | |||
| + | ===איחוד בן מנייה של קבוצות בנות מנייה=== | ||
| + | (בהנחת אקסיומת הבחירה) | ||
| + | |||
| + | *תהי S קבוצה בת מנייה של קבוצות בנות מנייה, כלומר: | ||
| + | **<math>|S|\leq\aleph_0</math> | ||
| + | **<math>\forall X\in S:|X|\leq\aleph_0</math> | ||
| + | *אזי גם האיחוד הכללי הוא בן מנייה: | ||
| + | **<math>|\cup_{X\in S}X|\leq \aleph_0</math> | ||
| + | |||
| + | |||
| + | *מסקנה: אוסף תתי הקבוצות הסופיות של המספרים הטבעיים הוא בן מנייה. | ||
| + | |||
| + | |||
| + | *הערה לסרטון: אנחנו משתמשים באקסיומת הבחירה כאשר "בוחרים" את הפונקציות החח"ע מהקבוצות באוסף אל הטבעיים. | ||
| + | |||
| + | |||
| + | <videoflash>0S6r0s2SnNc</videoflash> | ||
| + | |||
| + | ===השוואת עוצמות=== | ||
| + | (בהנחת עיקרון המקסימום של האוסדורף) | ||
| + | |||
| + | *תהיינה שתי קבוצות A,B אזי <math>|A|\leq|B|</math> או <math>|A|\geq |B|</math> | ||
| + | |||
| + | |||
| + | *נביט ב<math>U</math> אוסף היחסים הח"ע והחח"ע מ<math>A</math> ל<math>B</math>, וניקח שרשרת מקסימלית ביחס ההכלה <math>M\subseteq U</math> | ||
| + | *נסמן ב<math>f</math> את האיחוד הכללי על השרשרת <math>M</math> | ||
| + | *ראינו שנובע במקרה זה כי <math>f</math> יחס ח"ע וחח"ע מ<math>A</math> ל<math>B</math>. | ||
| + | **אם <math>f</math> שלם, אזי <math>f:A\to B</math> פונקציה חח"ע ולכן <math>|A|\leq |B|</math> | ||
| + | **אם <math>f</math> על, אזי <math>f:X\to B</math> פונקציה על עבור <math>X\subseteq A</math> ולכן <math>|B|\leq |X|\leq |A|</math> | ||
| + | **אחרת, קיים זוג <math>(a,b)\in A\times B</math> כך ש <math>f\cup\{(a,b)\}</math> יחס ח"ע וחח"ע שניתן להוסיף לשרשרת <math>M</math> בסתירה למקסימליות שלה. | ||
| + | |||
| + | |||
| + | <videoflash>XZkMt26fQyE</videoflash> | ||
| + | |||
| + | ====אלף אפס היא העוצמה האינסופית הקטנה ביותר==== | ||
| + | (בהנחת עקרון המקסימום של האוסדורף) | ||
| + | |||
| + | *תהי A קבוצה אינסופית, אזי <math>\aleph_0\leq |A|</math> | ||
| + | |||
| + | |||
| + | *דרך נוספת לזו המופיעה בסרטון: | ||
| + | **נוכיח בהמשך כי ניתן להשוות עוצמה בין כל שתי קבוצות | ||
| + | **אם <math>|A|\leq |\mathbb{N}|</math>, כיוון ש<math>A</math> אינסופית נובע כי <math>|A|=\aleph_0</math> | ||
| + | **אחרת, <math>|\mathbb{N}|\leq |A|</math> ולכן <math>\aleph_0\leq |A|</math> כפי שרצינו. | ||
| + | |||
| + | |||
| + | <videoflash>W4see8tTArk</videoflash> | ||
| + | |||
| + | |||
| + | |||
| + | *תהי A קבוצה אינסופית, ותהי B קבוצה סופית, אזי: | ||
| + | **<math>|A|=|A\cup B|=|A\setminus B|</math> | ||
| + | |||
| + | |||
| + | *דרך נוספת לזו המופיעה בסרטון: | ||
| + | **בהמשך נוכיח כי לכל קבוצה אינסופית <math>X</math> מתקיים כי <math>|X|+|X|=|X|</math> | ||
| + | **לכן <math>|A|\leq |A\cup B|=|A|+|B\setminus A|\leq |A|+|A|=|A|</math> ולפי ק.ש.ב <math>|A|=|A\cup B|</math>. | ||
| + | ***שימו לב כי <math>B\setminus A</math> סופית ולכן קטנה יותר מהקבוצה האינסופית <math>A</math>. | ||
| + | **כמו כן <math>|A|=|A\setminus B|+|B\cap A|</math> | ||
| + | **כעת <math>|A\setminus B|\leq|A\setminus B|+|B\cap A|\leq |A\setminus B|+|A\setminus B|=|A\setminus B|</math>. | ||
| + | ***שימו לב כי <math>B\cap A</math> סופית ולכן קטנה יותר מהקבוצה האינסופית <math>A\setminus B</math>. | ||
| + | **לכן לפי ק.ש.ב <math>|A|=|A\setminus B|+|B\cap A|=|A\setminus B|</math> | ||
| + | |||
| + | |||
| + | <videoflash>eaonM-yfR3w</videoflash> | ||
| + | |||
| + | ===סכום ומכפלה של עוצמות אינסופיות שווה לגדולה מבין העוצמות=== | ||
| + | |||
| + | *תהיינה עוצמות <math>a\leq b</math> אזי: | ||
| + | **<math>b\leq a+b</math> | ||
| + | *נניח בנוסף כי <math>2\leq a\leq b</math> אזי: | ||
| + | **<math>a+b\leq a\cdot b</math> | ||
| + | *נניח בנוסף כי b אינסופית, ונקבל ביחד | ||
| + | **<math>b\leq a+b \leq a\cdot b\leq b\cdot b =b</math> (המעבר <math>b\cdot b=b</math> מוכח בסרטון השני). | ||
| + | *ולכן לפי משפט ק.ש.ב נקבל כי | ||
| + | **<math>a+b=a\cdot b = b</math> | ||
| + | |||
| + | |||
| + | *דוגמא - מה היא עוצמת קבוצת המספרים האי-רציונאליים? | ||
| + | *<math>\mathbb{R}=\mathbb{Q}\cup (\mathbb{R}\setminus\mathbb{Q})</math> (איחוד זר כמובן) | ||
| + | *לכן <math>|\mathbb{R}|=|\mathbb{Q}|+ |(\mathbb{R}\setminus\mathbb{Q})|</math> | ||
| + | *לכן <math>\aleph=\aleph_0 +|(\mathbb{R}\setminus\mathbb{Q})|</math> | ||
| + | *לפי המשפט לעיל, סכום העוצמות הוא העוצמה הגדולה מבין השתיים. | ||
| + | *כיוון ש <math>\aleph\neq \aleph_0</math> נקבל כי <math>|(\mathbb{R}\setminus\mathbb{Q})|=\aleph</math> | ||
| + | |||
| + | |||
| + | <videoflash>Ty-lY6-uRPo</videoflash> | ||
| + | |||
| + | |||
| + | ====עוצמה כפול עצמה==== | ||
| + | *תהי קבוצה אינסופית <math>B</math> אזי <math>B\times B\sim B</math> | ||
| + | |||
| + | |||
| + | *הוכחה: | ||
| + | *תהי <math>S</math> קבוצת כל היחסים <math>R\subseteq (B\times B)\times B</math>, כך שקיימת תת קבוצה <math>X\subseteq B</math> כך ש <math>R:X\times X\to X</math> פונקציה הפיכה. | ||
| + | *כיוון ש<math>B</math> אינסופית, יש לה תת קבוצה <math>Y\subseteq B</math> כך ש <math>|Y|=\aleph_0</math>. | ||
| + | *כיוון ש <math>\aleph_0\times\aleph_0=\aleph_0</math> קיימת פונקציה הפיכה <math>R:Y\times Y\to Y</math>. | ||
| + | *נביט ביחס ההכלה על <math>S</math>. לפי עקרון המקסימום של האוסדורף, קיימת שרשרת מקסימלית <math>\{R\}\subseteq M\subseteq S</math>. | ||
| + | *נסמן ב<math>f</math> את האיחוד הכללי של השרשרת <math>f=\cup_{T\in M} T</math>. | ||
| + | *נוכיח כי קיימת <math>D\subseteq B</math> כך ש <math>f:D\times D\to D</math> פונקציה הפיכה, ואף <math>|D|=|B|</math> וכך נסיים את ההוכחה. | ||
| + | |||
| + | |||
| + | *הוכחה כי <math>f\in S</math> פונקציה הפיכה <math>f:D\times D\to D</math> עבור תת קבוצה <math>D\subseteq B</math>: | ||
| + | *ראשית, נגדיר את <math>D=\{d\in B | \exists a,b\in B:((a,b),d)\in f\}</math> | ||
| + | *נוכיח כי <math>f\subseteq (D\times D)\times D</math>: | ||
| + | **יהי זוג <math>((a,b),d)\in f</math>, לפי ההגדרה <math>d\in D</math> | ||
| + | **כמו כן, לפי הגדרת האיחוד קיים <math>T\in M</math> כך ש <math>((a,b),d)\in T</math>. | ||
| + | **קיימת <math>X\subseteq B</math> כך ש <math>T:X\times X\to X</math> פונקציה הפיכה. | ||
| + | **כיוון ש <math>T</math> על, לכל <math>x\in X</math> קיימים <math>p,q\in X</math> כך ש <math>((p,q),x)\in T</math> ולכן <math>((p,q),x)\in f</math> ולכן <math>x\in D</math> | ||
| + | **ביחד עם העובדה ש <math>a,b\in X</math> נובע כי <math>a,b\in D</math> | ||
| + | *כיוון שכל איברי השרשרת הם יחסים ח"ע, גם <math>f</math> ח"ע. | ||
| + | *כיוון שכל איברי השרשרת הם יחסים חח"ע, גם <math>f</math> חח"ע. | ||
| + | *כעת נוכיח כי <math>f:D\times D\to D</math> יחס שלם: | ||
| + | **יהיו <math>d_1,d_2\in D</math>. | ||
| + | **ראינו כי קיימים <math>T_1,T_2\in M</math> ואיברים <math>a_1,b_1,a_2,b_2\in D</math> כך ש <math>((a_1,b_1),d_1)\in T_1</math> וכן <math>((a_2,b_2),d_2)\in T_2</math> | ||
| + | **כיוון ש<math>M</math> שרשרת, <math>T_1\subseteq T_2</math> (או ההפך) ולכן <math>a_1,a_2,b_1,b_2\in X</math> עבור תת קבוצה <math>X\subseteq D</math> כך ש <math>T_2:X\times X\to X</math> פונקציה הפיכה. | ||
| + | **לכן קיים <math>d_3\in X\subseteq D</math> כך ש <math>((d_1,d_2),d_3)\in T_2</math> ולכן <math>((d_1,d_2),d_3)\in f</math> כלומר <math>f</math> שלם. | ||
| + | *הוכחנו כי <math>f:D\times D\to D</math> היא פונקציה (יחס ח"ע ושלם) חח"ע, נותר להוכיח כי היא על: | ||
| + | **יהי <math>d\in D</math>. ראינו כי קיים <math>T\in M</math> וקיימים <math>a,b\in D</math> כך ש <math>((a,b),d)\in T</math> ולכן <math>((a,b),d)\in f</math> ולכן הפונקציה על. | ||
| + | |||
| + | |||
| + | *הוכחה כי <math>|D|=|B|</math>: | ||
| + | *ראשית, נשים לב כי <math>Y\subseteq D</math> כיוון ש <math>R:Y\times Y\to Y</math> פונקציה הפיכה וכן <math>R\in M</math>, ולכן <math>D</math> אינסופית. | ||
| + | *כעת, נזכור שהוכחנו כי <math>|D\times D|=|D|</math>. | ||
| + | *נביט ב <math>B\setminus D</math> ונחלק למקרים: | ||
| + | *אם <math>|B\setminus D|\leq D</math> אזי: | ||
| + | **<math>|B|=|D|+|B\setminus D|\leq |D|+|D|\leq |D|\times |D| =|D|</math> | ||
| + | **כמובן ש <math>|D|\leq |B|</math> ולפי ק.ש.ב נסיק כי במקרה זה <math>|B|=|D|</math> וסיימנו. | ||
| + | *אם <math>|B\setminus D|\geq |D|</math> נראה כי נגיע לסתירה, ולכן מקרה זה בלתי אפשרי: | ||
| + | **ניקח תת קבוצה <math>U\subseteq B\setminus D</math> כך ש <math>|U|=|D|</math>. | ||
| + | **לכן <math>|(U\times D) \cup (D\times U) \cup (U\times U)|=|D|+|D|+|D|=|D|</math> (הרי ראינו מקודם כי <math>|D|+|D|=|D|</math>) | ||
| + | **לכן קיימת פונקציה הפיכה <math>g:(U\times D) \cup (D\times U) \cup (U\times U)\to U</math>. | ||
| + | **האיחוד <math>h=f\cup g</math> הוא פונקציה הפיכה <math>h:(U\cup D)\times (U\cup D)\to (U\cup D)</math>, ולכן <math>h\in S</math>. | ||
| + | **ניתן להוסיף את <math>h</math> לשרשרת <math>M</math> ולהגדיל אותה, בסתירה למקסימליות שלה. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <videoflash>e6cBpbJzs2A</videoflash> | ||
| + | |||
| + | ===הקשר בין עוצמת הטבעיים לעוצמת הממשיים=== | ||
| + | |||
| + | *<math>2^{\aleph_0}=\aleph</math> כלומר <math> P(\mathbb{N})\sim\mathbb{R}</math> | ||
| + | |||
| + | |||
| + | <videoflash>dhrT0edcmJE</videoflash> | ||
===תרגול=== | ===תרגול=== | ||
גרסה אחרונה מ־07:35, 18 ביולי 2023
תוכן עניינים
- 1 חומר עזר
- 2 סרטוני ותקציר הרצאות
- 2.1 פרק 1 - מבוא ללוגיקה מתמטית
- 2.2 פרק 2 - מבוא לתורת הקבוצות
- 2.3 פרק 3 - יחסים
- 2.4 פרק 4 - פונקציות
- 2.5 פרק 5 - עוצמות
- 2.5.1 מבוא
- 2.5.2 השוואת עוצמות
- 2.5.3 משפט קנטור
- 2.5.4 קבוצות בנות מנייה
- 2.5.5 חשבון עוצמות (אריתמטיקה של עוצמות)
- 2.5.6 משפט קנטור-שרדר-ברנשטיין
- 2.5.7 אקסיומת הבחירה ועקרון המקסימום של האוסדורף
- 2.5.8 איחוד בן מנייה של קבוצות בנות מנייה
- 2.5.9 השוואת עוצמות
- 2.5.10 סכום ומכפלה של עוצמות אינסופיות שווה לגדולה מבין העוצמות
- 2.5.11 הקשר בין עוצמת הטבעיים לעוצמת הממשיים
- 2.5.12 תרגול
חומר עזר
- סיכומי ההרצאות של ד״ר ארז שיינר, ע״י אורית חסון, קיץ 2016
- מבחנים בבדידה
- בחנים בבדידה
- מבחנים בקורס בדידה למורים - שימו לב, הקורס למורים מכיל משמעותית פחות חומר, והמבחנים קלים יותר. יחד עם זאת, יש שם כמות גדולה של תרגילים רלוונטיים ברמה נמוכה.
סרטוני ותקציר הרצאות
פרק 1 - מבוא ללוגיקה מתמטית
פסוקים, קשרים, כמתים, פרדיקטים
תרגול
אינדוקציה
- משפט האינדוקציה המתמטית
- תהי סדרת טענות כך שמתקיימים שני התנאים הבאים:
- הטענה הראשונה נכונה.
- לכל
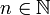 אם הטענה הn מתקיימת אז גם הטענה הn+1 מתקיימת.
אם הטענה הn מתקיימת אז גם הטענה הn+1 מתקיימת.
- אזי כל הטענות בסדרה נכונות
- דוגמא:
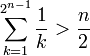
- אינדוקציה שלמה (מלאה)
- תהי סדרת טענות כך ש:
- לכל
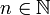 אם כל הטענות עד ולא כולל הטענה הn מתקיימות, אזי גם הטענה הn מתקיימת.
אם כל הטענות עד ולא כולל הטענה הn מתקיימות, אזי גם הטענה הn מתקיימת.
- לכל
- אזי כל הטענות בסדרה מתקיימות.
- שימו לב: לפני הטענה הראשונה אין טענות, ולכן כולן מתקיימות באופן ריק. כלומר מנוסח התנאי נובע שצריך להוכיח שהטענה הראשונה מתקיימת.
- פרדוקס הסוסים (או פתיתי השלג)
תרגול
פרק 2 - מבוא לתורת הקבוצות
קבוצות ופעולות על קבוצות
- איבר שייך לקבוצה
 אם הוא אחד האיברים בקבוצה.
אם הוא אחד האיברים בקבוצה. - קבוצה מוכלת בקבוצה אחרת
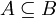 אם
אם 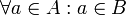
- תהי קבוצה
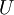 ותהיינה
ותהיינה 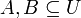 . נגדיר את:
. נגדיר את:
- קבוצת האיחוד
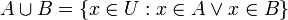
- קבוצת החיתוך
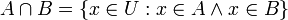
- קבוצת ההפרש
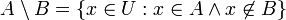
- קבוצת ההפרש הסימטרי
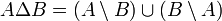
- קבוצת המשלים
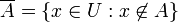
- קבוצת האיחוד
שיטות הוכחה בסיסיות
- הוכחת טענות מכומתות - טענות 'לכל' וטענות 'קיים'
- הוכחת הכלה בין קבוצות, ושיוויון בין קבוצות
איחוד וחיתוך כלליים
- תהי S קבוצה של קבוצות, נגדיר:
קבוצת החזקה
תרגול
פרק 3 - יחסים
מכפלה קרטזית ויחסים
תכונות של יחסים
- יהי R יחס על A (כלומר
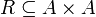 ) אזי:
) אזי:
- R נקרא רפלקסיבי אם לכל
 מתקיים
מתקיים 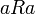 .
. - R נקרא סימטרי אם לכל
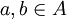 המקיימים
המקיימים 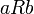 מתקיים
מתקיים 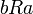
- R נקרא אנטי-סימטרי אם לכל
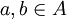 המקיימים
המקיימים 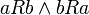 מתקיים
מתקיים 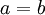
- R נקרא טרנזיטיבי אם לכל
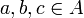 המקיימים
המקיימים 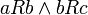 מתקיים
מתקיים 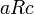
- R נקרא מלא אם לכל
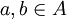 מתקיים כי
מתקיים כי 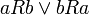
- R נקרא רפלקסיבי אם לכל
- יהי R יחס מA לB (כלומר
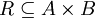 ) אזי:
) אזי:
- R נקרא חד-ערכי (ח"ע) אם לכל
 ולכל
ולכל 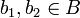 המקיימים
המקיימים 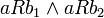 מתקיים
מתקיים 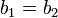
- R נקרא שלם אם לכל
 קיים
קיים 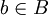 כך ש
כך ש 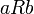
- R נקרא חד-חד-ערכי (חח"ע) אם לכל
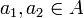 ולכל
ולכל 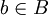 המקיימים
המקיימים 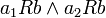 מתקיים
מתקיים 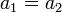
- R נקרא על אם לכל
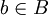 קיים
קיים  כך ש
כך ש 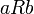
- R נקרא חד-ערכי (ח"ע) אם לכל
יחסי שקילות
- יחס R על קבוצה A נקרא יחס שקילות אם הוא רפלקסיבי, סימטרי וטרנזיטיבי.
- יהי R יחס שקילות על A.
- לכל
 מוגדרת קבוצת מחלקת השקילות של a ע"י:
מוגדרת קבוצת מחלקת השקילות של a ע"י:
- קבוצת כל קבוצות מחלקות השקילות נקראת קבוצת המנה:
- תהי קבוצה A. קבוצת תתי קבוצות
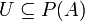 נקראת חלוקה של A אם:
נקראת חלוקה של A אם:
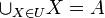
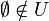
- לכל
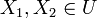 אם
אם 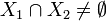 אזי
אזי 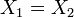
- היחס המושרה מחלוקה:
- תהי קבוצה A ותהי חלוקה שלה U. נגדיר יחס R על A על ידי:
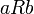 אם ורק אם קיימת
אם ורק אם קיימת 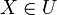 כך ש
כך ש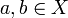
- היחס המושרה מחלוקה הוא יחס שקילות.
- קבוצת המנה היא חלוקה של A.
- היחס המושרה מקבוצת המנה, הוא יחס השקילות המקורי; קבוצת המנה של יחס שקילות מושרה היא החלוקה המקורית.
תרגול
יחסי סדר
- יחס R על קבוצה A נקרא יחס סדר חלקי אם הוא רפלקסיבי, אנטי-סימטרי וטרנזיטיבי
איברים מינימליים ומקסימליים, וחסמים
- יהי R יחס סדר חלקי על קבוצה X, ותהי
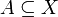 תת קבוצה.
תת קבוצה.
- איבר
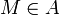 נקרא מקסימלי בA אם לכל
נקרא מקסימלי בA אם לכל  המקיים
המקיים 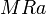 מתקיים כי
מתקיים כי 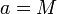 (אין גדולים ממנו)
(אין גדולים ממנו) - איבר
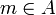 נקרא מינימלי בA אם לכל
נקרא מינימלי בA אם לכל  המקיים
המקיים 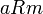 מתקיים כי
מתקיים כי 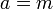 (אין קטנים ממנו)
(אין קטנים ממנו) - איבר
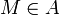 נקרא הגדול ביותר (מקסימום) בA אם לכל
נקרא הגדול ביותר (מקסימום) בA אם לכל  מתקיים
מתקיים 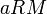 (הוא גדול מכולם)
(הוא גדול מכולם) - איבר
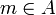 נקרא הקטן ביותר (מינימום) בA אם לכל
נקרא הקטן ביותר (מינימום) בA אם לכל  מתקיים
מתקיים 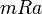 (הוא קטן מכולם)
(הוא קטן מכולם) - איבר
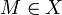 נקרא חסם מלעיל של A אם לכל
נקרא חסם מלעיל של A אם לכל  מתקיים
מתקיים 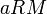 (הוא גדול מכל איברי הקבוצה, אבל לאו דווקא נמצא בקבוצה)
(הוא גדול מכל איברי הקבוצה, אבל לאו דווקא נמצא בקבוצה) - איבר
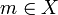 נקרא חסם מלרע של A אם לכל
נקרא חסם מלרע של A אם לכל  מתקיים
מתקיים 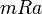 (הוא קטן מכל איברי הקבוצה, אבל לאו דווקא נמצא בקבוצה)
(הוא קטן מכל איברי הקבוצה, אבל לאו דווקא נמצא בקבוצה) - אם בקבוצת חסמי המלעיל של A יש איבר קטן ביותר הוא נקרא חסם עליון (supremum) של A.
- אם בקבוצת חסמי המלרע של A יש איבר גדול ביותר הוא נקרא חסם תחתון (infimum) של A.
- איבר
- איבר גדול ביותר ביותר הוא יחיד.
- אם חסם מלעיל שייך לקבוצה, אז הוא הגדול ביותר.
- האיבר הגדול ביותר בקבוצה הוא איבר מקסימלי, ואין איברים מקסימליים אחרים.
- האם תתכן קבוצה עם איבר מקסימלי יחיד שאינו האיבר הגדול ביותר בקבוצה?
- ביחס ההכלה על קבוצת חזקה, האיחוד הכללי של קבוצת קבוצות הוא החסם העליון שלה, והחיתוך הכללי הוא החסם התחתון.
- ביחס 'מחלק את' על הטבעיים, המחלק המשותף המקסימלי הוא החסם התחתון, והמכפלה המשותפת המינימלית הוא החסם העליון.
שרשראות
- יחס סדר חלקי R על A נקרא מלא (או לינארי, או קווי) אם:
- יהי R יחס סדר חלקי על A, ותהי
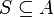 .
. - אזי
 נקראת שרשרת אם היחס מלא עליה, כלומר
נקראת שרשרת אם היחס מלא עליה, כלומר 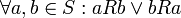
תרגול
פרק 4 - פונקציות
הגדרת פונקציות
- יחס f מA לB נקרא פונקציה אם הוא ח"ע ושלם, ומסמנים במקרה זה
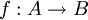 , וכן
, וכן 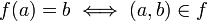 .
. - A נקרא תחום הפונקציה (או תחום הגדרה), B נקרא הטווח של הפונקציה.
- שימו לב, הסרטון ישן, ושם פונקציה הוגדרה כיחס ח"ע בלבד, בניגוד להגדרה העדכנית שלנו בקורס.
חח"ע ועל, תמונה ותמונה הפוכה
- תהי
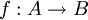 פונקציה. אזי:
פונקציה. אזי:
- f חח"ע אם לכל
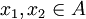 המקיימים
המקיימים 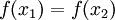 מתקיים כי
מתקיים כי 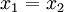
- f על אם לכל
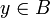 קיים
קיים 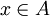 כך ש
כך ש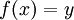
- תהי
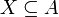 נגדיר את קבוצת התמונה
נגדיר את קבוצת התמונה ![f[X]=\{f(a)|a\in X\}](/images/math/5/5/7/55779957b3f7ea329439f157161be86c.png)
- תהי
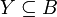 נגדיר את קבוצת התמונה ההפוכה
נגדיר את קבוצת התמונה ההפוכה ![f^{-1}[Y]=\{a\in A|f(a)\in Y\}](/images/math/c/5/7/c573ed3afce2ddff9613aebd0c435561.png)
![f[]:P(A)\to P(B)](/images/math/5/9/5/5953df04b1b8d07c6e1a718cc54d1e3a.png) היא פונקצית התמונה, השולחת כל תת קבוצה לקבוצת התמונה שלה
היא פונקצית התמונה, השולחת כל תת קבוצה לקבוצת התמונה שלה![f^{-1}[]:P(B)\to P(A)](/images/math/0/1/f/01f3ca21d2ca4ab5d188dbccaa0820c7.png) היא פונקצית התמונה ההפוכה, השולחת כל תת קבוצה לקבוצת התמונה ההפוכה שלה
היא פונקצית התמונה ההפוכה, השולחת כל תת קבוצה לקבוצת התמונה ההפוכה שלה
- f חח"ע אם לכל
- שימו לב
הרכבת פונקציות, פונקציות הפיכות
- תהיינה
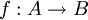 וכן
וכן 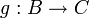 אזי נגדיר את פונקצית ההרכבה
אזי נגדיר את פונקצית ההרכבה 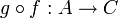 ע"י
ע"י 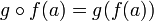
- פעולת ההרכבה היא אסוציאטיבית.
- תהי קבוצה A נגדיר את פונקצית הזהות
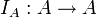 ע"י
ע"י 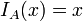 .
. - לכל פונקציה
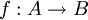 מתקיים כי
מתקיים כי 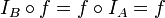
- פונקציה
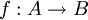 נקראת הפיכה אם קיימות פונקציות
נקראת הפיכה אם קיימות פונקציות 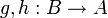 כך ש:
כך ש:
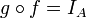 וכן
וכן 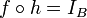
- נשים לב כי
- לכן אם פונקציה הפיכה, יש פונקציה יחידה שהופכת אותה (ההופכית), נסמנה
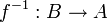 .
. - שימו לב: עם סוגריים מרובעים זו פונקצית התמונה ההפוכה שיש לכל פונקציה ופועלת על תתי קבוצות, עם סוגריים עגולים זו הפונקציה ההופכית שיש רק להפיכות ופועלת על איברים.
פונקציה מוגדרת היטב
תרגול
פרק 5 - עוצמות
מבוא
השוואת עוצמות
- A שקולת עוצמה לB או עוצמתה של A שווה לB, אם קיימת פונקציה הפיכה (חח"ע ועל)
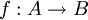 .
. - במקרה זה מסמנים
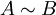 או
או 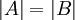 .
.
- כל קבוצה שקולת עוצמה לעצמה
- אם A שקולת עוצמה לB, גם B שקולת עוצמה לA
- אם A שקולת עוצמה לB וB שקולת עוצמה לC אזי A שקולת עוצמה לC
- עוצמתה של A קטנה או שווה לזו של B, אם קיימת פונקציה חח"ע
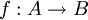 .
. - במקרה זה מסמנים
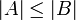
- כל קבוצה A השקולת עוצמה לקבוצת הטבעיים מסומנת
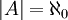
- כל קבוצה A השקולת עוצמה לקבוצת הממשיים מסומנת
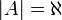
משפט קנטור
קבוצות בנות מנייה
- קבוצה A נקראת בת מנייה אם
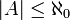
- כל קבוצה A בת מנייה אינסופית מקיימת
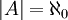
חשבון עוצמות (אריתמטיקה של עוצמות)
חיבור עוצמות
- תהיינה שתי עוצמות a,b ותהיינה שתי נציגות זרות לעוצמות A,B.
- נגדיר
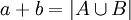 , הגדרה זו אינה תלוייה בבחירת הנציגות.
, הגדרה זו אינה תלוייה בבחירת הנציגות.
כפל עוצמות
- תהיינה שתי עוצמות a,b ותהיינה שתי נציגות לעוצמות A,B.
- נגדיר
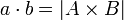 , הגדרה זו אינה תלוייה בבחירת הנציגות.
, הגדרה זו אינה תלוייה בבחירת הנציגות.
חזקת עוצמות
- תהיינה שתי עוצמות a,b ותהיינה שתי נציגות לעוצמות A,B.
- נגדיר את
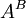 להיות אוסף כל הפונקציות מB לA (מהמעריך לבסיס).
להיות אוסף כל הפונקציות מB לA (מהמעריך לבסיס). - נגדיר
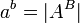 , הגדרה זו אינה תלוייה בבחירת הנציגות.
, הגדרה זו אינה תלוייה בבחירת הנציגות.
- חוקי חזקות
- תהיינה עוצמות a,b,c אזי
עוצמת קבוצת החזקה
השוואת חשבון עוצמות
- תהיינה עוצמות a,b,c,d כך ש
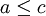 וכן
וכן 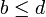 אזי:
אזי:
- אם בנוסף נתון כי
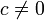 אזי
אזי
משפט קנטור-שרדר-ברנשטיין
- אם
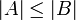 וגם
וגם 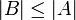 אזי
אזי 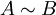
למת נקודת השבת
- תהי פונקציה עולה
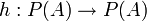 כלומר המקיימת לכל
כלומר המקיימת לכל 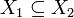 כי
כי 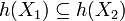
- אזי קיימת נק' שבת
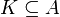 כך ש
כך ש 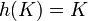 .
.
הוכחת המשפט
עוצמות קטעים ממשיים
אקסיומת הבחירה ועקרון המקסימום של האוסדורף
אקסיומת הבחירה
- תהי S קבוצת קבוצות לא ריקות, ונסמן את האיחוד הכללי ב
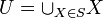 .
. - אזי קיימת פונקצית בחירה
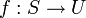 הבוחרת איבר מתוך כל קבוצה, כלומר:
הבוחרת איבר מתוך כל קבוצה, כלומר:
- דוגמא:
- תהי פונקציה על
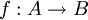 אזי קיימת תת קבוצה
אזי קיימת תת קבוצה 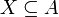 כך ש
כך ש 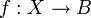 חח"ע ועל.
חח"ע ועל.
- תהי פונקציה על
- תהיינה
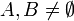 אזי
אזי 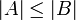 אם ורק אם קיימת
אם ורק אם קיימת 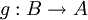 על.
על.
- בכיוון ראשון:
- תהי
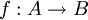 חח"ע
חח"ע - כיוון ש
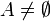 קיים
קיים 
- נגדיר פונקציה
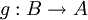 באופן הבא:
באופן הבא:
- לכל
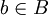
- אם קיים
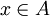 כך ש
כך ש 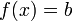 נגדיר
נגדיר 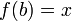 (בגלל החח"ע זה מוגדר היטב)
(בגלל החח"ע זה מוגדר היטב) - אם
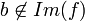 נגדיר
נגדיר 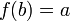
- לכל
- הפונקציה
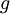 שהגדרנו היא אכן על, כי לכל
שהגדרנו היא אכן על, כי לכל 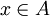 מתקיים כי
מתקיים כי 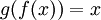
- תהי
- בכיוון שני:
- תהי
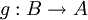 על, אזי כל הקבוצות באוסף
על, אזי כל הקבוצות באוסף ![U=\left\{g^{-1}[\{a\}]|a\in A\right\}](/images/math/0/f/4/0f49d90bffee339fd4640d6c8cbabaf2.png) אינן ריקות.
אינן ריקות. - ניקח פונקצית בחירה
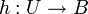 ונגדיר
ונגדיר 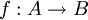 ע"י
ע"י ![f(a)=h(g^{-1}[\{a\}])](/images/math/5/4/c/54c78ea515fb0916fd9eef54fa15cd4e.png)
- אכן
 חח"ע כי אם
חח"ע כי אם 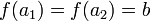 אזי
אזי ![b\in g^{-1}[\{a_1\}]](/images/math/a/8/2/a820a5e85eaab2493c00ddbb32fcad1a.png) וכן
וכן ![b\in g^{-1}[\{a_2\}]](/images/math/3/a/1/3a17d0dffb1688ffcf8a19c41a03a504.png)
- ולכן
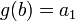 וכן
וכן 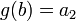 , כלומר
, כלומר 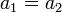
- תהי
עקרון המקסימום של האוסדורף
- תהי קבוצה A עם יחס סדר חלקי, תת קבוצה
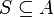 נקראת שרשרת אם היחס מלא עליה (ניתן להשוות בין כל שני איברים בS).
נקראת שרשרת אם היחס מלא עליה (ניתן להשוות בין כל שני איברים בS). - שרשרת נקראת מקסימלית בA אם היא אינה מוכלת באף שרשרת אחרת.
- עקרון המקסימום של האוסדורף אומר שכל שרשרת מוכלת בשרשרת מקסימלית.
- דוגמא - אוסף עיגולים במישור שאינם חותכים זה את זה, ולא ניתן להוסיף אפילו עיגול אחד נוסף.
- טענות שימושיות להמשך:
- תהי
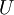 קבוצה של יחסים מ
קבוצה של יחסים מ ל
ל  , תהי
, תהי 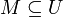 שרשרת ביחס ההכלה ונסמן את האיחוד הכללי של השרשרת ב
שרשרת ביחס ההכלה ונסמן את האיחוד הכללי של השרשרת ב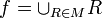
- אזי:
- אם כל היחסים ב
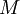 ח"ע, אז גם
ח"ע, אז גם  ח"ע
ח"ע
- אכן, יהיו
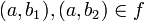
- לכן קיימים
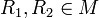 כך ש
כך ש 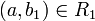 וכן
וכן 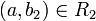
- כיוון ש
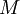 שרשרת, אזי
שרשרת, אזי 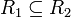 (או ההפך) ולכן
(או ההפך) ולכן 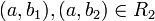
- כיוון ש
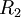 ח"ע נובע כי
ח"ע נובע כי 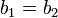 כפי שרצינו.
כפי שרצינו.
- אכן, יהיו
- אם כל היחסים ב
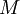 חח"ע, אזי גם
חח"ע, אזי גם  חח"ע
חח"ע
- הוכחה דומה לח"ע
- אם כל היחסים ב
איחוד בן מנייה של קבוצות בנות מנייה
(בהנחת אקסיומת הבחירה)
- תהי S קבוצה בת מנייה של קבוצות בנות מנייה, כלומר:
- אזי גם האיחוד הכללי הוא בן מנייה:
- מסקנה: אוסף תתי הקבוצות הסופיות של המספרים הטבעיים הוא בן מנייה.
- הערה לסרטון: אנחנו משתמשים באקסיומת הבחירה כאשר "בוחרים" את הפונקציות החח"ע מהקבוצות באוסף אל הטבעיים.
השוואת עוצמות
(בהנחת עיקרון המקסימום של האוסדורף)
- תהיינה שתי קבוצות A,B אזי
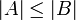 או
או 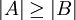
- נביט ב
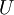 אוסף היחסים הח"ע והחח"ע מ
אוסף היחסים הח"ע והחח"ע מ ל
ל , וניקח שרשרת מקסימלית ביחס ההכלה
, וניקח שרשרת מקסימלית ביחס ההכלה 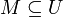
- נסמן ב
 את האיחוד הכללי על השרשרת
את האיחוד הכללי על השרשרת 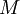
- ראינו שנובע במקרה זה כי
 יחס ח"ע וחח"ע מ
יחס ח"ע וחח"ע מ ל
ל .
.
- אם
 שלם, אזי
שלם, אזי 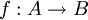 פונקציה חח"ע ולכן
פונקציה חח"ע ולכן 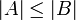
- אם
 על, אזי
על, אזי 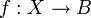 פונקציה על עבור
פונקציה על עבור 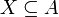 ולכן
ולכן 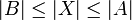
- אחרת, קיים זוג
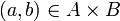 כך ש
כך ש 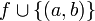 יחס ח"ע וחח"ע שניתן להוסיף לשרשרת
יחס ח"ע וחח"ע שניתן להוסיף לשרשרת 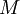 בסתירה למקסימליות שלה.
בסתירה למקסימליות שלה.
- אם
אלף אפס היא העוצמה האינסופית הקטנה ביותר
(בהנחת עקרון המקסימום של האוסדורף)
- תהי A קבוצה אינסופית, אזי
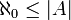
- דרך נוספת לזו המופיעה בסרטון:
- נוכיח בהמשך כי ניתן להשוות עוצמה בין כל שתי קבוצות
- אם
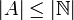 , כיוון ש
, כיוון ש אינסופית נובע כי
אינסופית נובע כי 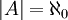
- אחרת,
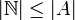 ולכן
ולכן 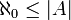 כפי שרצינו.
כפי שרצינו.
- תהי A קבוצה אינסופית, ותהי B קבוצה סופית, אזי:
- דרך נוספת לזו המופיעה בסרטון:
- בהמשך נוכיח כי לכל קבוצה אינסופית
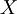 מתקיים כי
מתקיים כי 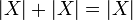
- לכן
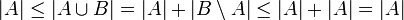 ולפי ק.ש.ב
ולפי ק.ש.ב 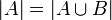 .
.
- שימו לב כי
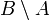 סופית ולכן קטנה יותר מהקבוצה האינסופית
סופית ולכן קטנה יותר מהקבוצה האינסופית  .
.
- שימו לב כי
- כמו כן
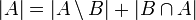
- כעת
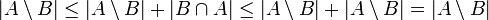 .
.
- שימו לב כי
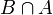 סופית ולכן קטנה יותר מהקבוצה האינסופית
סופית ולכן קטנה יותר מהקבוצה האינסופית 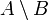 .
.
- שימו לב כי
- לכן לפי ק.ש.ב
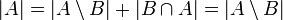
- בהמשך נוכיח כי לכל קבוצה אינסופית
סכום ומכפלה של עוצמות אינסופיות שווה לגדולה מבין העוצמות
- תהיינה עוצמות
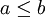 אזי:
אזי:
- נניח בנוסף כי
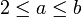 אזי:
אזי:
- נניח בנוסף כי b אינסופית, ונקבל ביחד
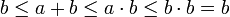 (המעבר
(המעבר 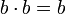 מוכח בסרטון השני).
מוכח בסרטון השני).
- ולכן לפי משפט ק.ש.ב נקבל כי
- דוגמא - מה היא עוצמת קבוצת המספרים האי-רציונאליים?
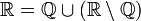 (איחוד זר כמובן)
(איחוד זר כמובן)- לכן
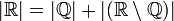
- לכן
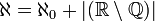
- לפי המשפט לעיל, סכום העוצמות הוא העוצמה הגדולה מבין השתיים.
- כיוון ש
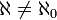 נקבל כי
נקבל כי 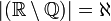
עוצמה כפול עצמה
- תהי קבוצה אינסופית
 אזי
אזי 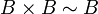
- הוכחה:
- תהי
 קבוצת כל היחסים
קבוצת כל היחסים 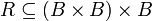 , כך שקיימת תת קבוצה
, כך שקיימת תת קבוצה 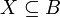 כך ש
כך ש 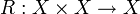 פונקציה הפיכה.
פונקציה הפיכה. - כיוון ש
 אינסופית, יש לה תת קבוצה
אינסופית, יש לה תת קבוצה 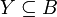 כך ש
כך ש 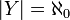 .
. - כיוון ש
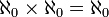 קיימת פונקציה הפיכה
קיימת פונקציה הפיכה 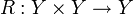 .
. - נביט ביחס ההכלה על
 . לפי עקרון המקסימום של האוסדורף, קיימת שרשרת מקסימלית
. לפי עקרון המקסימום של האוסדורף, קיימת שרשרת מקסימלית 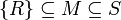 .
. - נסמן ב
 את האיחוד הכללי של השרשרת
את האיחוד הכללי של השרשרת 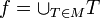 .
. - נוכיח כי קיימת
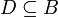 כך ש
כך ש 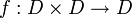 פונקציה הפיכה, ואף
פונקציה הפיכה, ואף 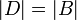 וכך נסיים את ההוכחה.
וכך נסיים את ההוכחה.
- הוכחה כי
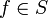 פונקציה הפיכה
פונקציה הפיכה 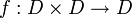 עבור תת קבוצה
עבור תת קבוצה 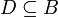 :
: - ראשית, נגדיר את
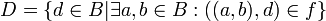
- נוכיח כי
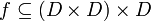 :
:
- יהי זוג
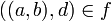 , לפי ההגדרה
, לפי ההגדרה 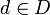
- כמו כן, לפי הגדרת האיחוד קיים
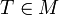 כך ש
כך ש 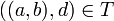 .
. - קיימת
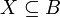 כך ש
כך ש 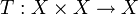 פונקציה הפיכה.
פונקציה הפיכה. - כיוון ש
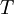 על, לכל
על, לכל 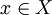 קיימים
קיימים 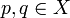 כך ש
כך ש 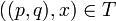 ולכן
ולכן 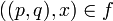 ולכן
ולכן 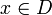
- ביחד עם העובדה ש
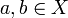 נובע כי
נובע כי 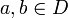
- יהי זוג
- כיוון שכל איברי השרשרת הם יחסים ח"ע, גם
 ח"ע.
ח"ע. - כיוון שכל איברי השרשרת הם יחסים חח"ע, גם
 חח"ע.
חח"ע. - כעת נוכיח כי
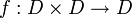 יחס שלם:
יחס שלם:
- יהיו
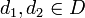 .
. - ראינו כי קיימים
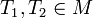 ואיברים
ואיברים 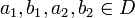 כך ש
כך ש 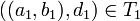 וכן
וכן 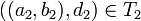
- כיוון ש
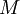 שרשרת,
שרשרת, 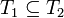 (או ההפך) ולכן
(או ההפך) ולכן 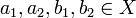 עבור תת קבוצה
עבור תת קבוצה 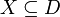 כך ש
כך ש 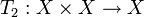 פונקציה הפיכה.
פונקציה הפיכה. - לכן קיים
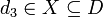 כך ש
כך ש 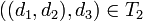 ולכן
ולכן 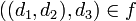 כלומר
כלומר  שלם.
שלם.
- יהיו
- הוכחנו כי
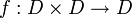 היא פונקציה (יחס ח"ע ושלם) חח"ע, נותר להוכיח כי היא על:
היא פונקציה (יחס ח"ע ושלם) חח"ע, נותר להוכיח כי היא על:
- יהי
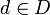 . ראינו כי קיים
. ראינו כי קיים 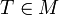 וקיימים
וקיימים 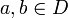 כך ש
כך ש 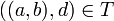 ולכן
ולכן 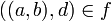 ולכן הפונקציה על.
ולכן הפונקציה על.
- יהי
- הוכחה כי
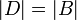 :
: - ראשית, נשים לב כי
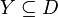 כיוון ש
כיוון ש 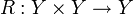 פונקציה הפיכה וכן
פונקציה הפיכה וכן 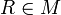 , ולכן
, ולכן 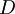 אינסופית.
אינסופית. - כעת, נזכור שהוכחנו כי
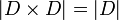 .
. - נביט ב
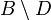 ונחלק למקרים:
ונחלק למקרים: - אם
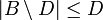 אזי:
אזי:
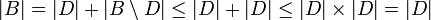
- כמובן ש
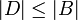 ולפי ק.ש.ב נסיק כי במקרה זה
ולפי ק.ש.ב נסיק כי במקרה זה 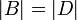 וסיימנו.
וסיימנו.
- אם
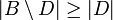 נראה כי נגיע לסתירה, ולכן מקרה זה בלתי אפשרי:
נראה כי נגיע לסתירה, ולכן מקרה זה בלתי אפשרי:
- ניקח תת קבוצה
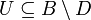 כך ש
כך ש 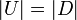 .
. - לכן
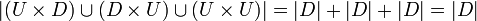 (הרי ראינו מקודם כי
(הרי ראינו מקודם כי 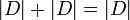 )
) - לכן קיימת פונקציה הפיכה
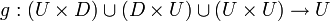 .
. - האיחוד
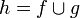 הוא פונקציה הפיכה
הוא פונקציה הפיכה 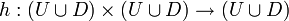 , ולכן
, ולכן 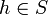 .
. - ניתן להוסיף את
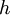 לשרשרת
לשרשרת 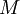 ולהגדיל אותה, בסתירה למקסימליות שלה.
ולהגדיל אותה, בסתירה למקסימליות שלה.
- ניקח תת קבוצה
הקשר בין עוצמת הטבעיים לעוצמת הממשיים
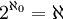 כלומר
כלומר 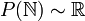
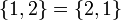
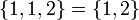
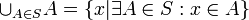
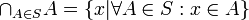
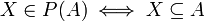
![[a]_R=\{x\in A|aRx\}](/images/math/7/c/9/7c9faa884e0a4a3c5b7250215de49ebc.png)
![A/R=\{[a]_R:a\in A\}](/images/math/e/1/b/e1b752a1a51d5a8c2739f86e8a3aea8a.png)
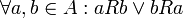
![x\in f^{-1}[Y]\iff f(x)\in Y](/images/math/3/c/0/3c0c93dee0ad9d3c048187afe325322f.png)
![y\in f[X] \iff \exist a\in X :f(a)=y](/images/math/4/1/f/41f00f92b710f296b02011df4ae6b7dc.png)
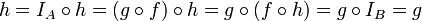
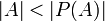
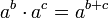
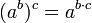
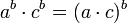
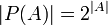
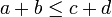
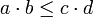
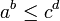
![|\mathbb{R}|=|[a,\infty)|=|[a,b]|=|(a,b)|=\aleph](/images/math/e/2/8/e28f470d9989f90392ac879da050605e.png)