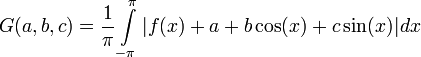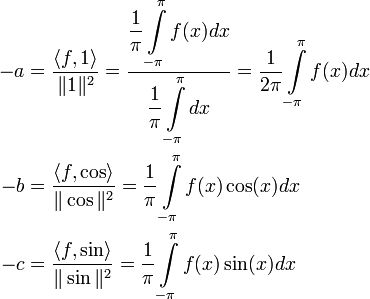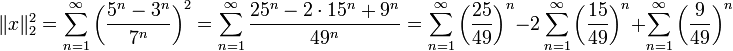הבדלים בין גרסאות בדף "אנליזת פורייה ויישומים קיץ תשעב/סיכומים/הרצאות/1.8.12"
יהודה שמחה (שיחה | תרומות) (הגהה, שיפוץ קודים מתמטיים) |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 2: | שורה 2: | ||
'''הגדרה:''' הפונקציה <math>f:[-\pi,\pi]\to\C</math> תקרא ''רציפה למקוטעין'' אם: | '''הגדרה:''' הפונקציה <math>f:[-\pi,\pi]\to\C</math> תקרא ''רציפה למקוטעין'' אם: | ||
:#ל־<math>f</math> יש לכל היותר מספר סופי של נקודות אי־רציפות. | :#ל־<math>f</math> יש לכל היותר מספר סופי של נקודות אי־רציפות. | ||
| − | :#בכל נקודת אי־רציפות קיימים הגבולות | + | :#בכל נקודת אי־רציפות קיימים הגבולות החד־צדדיים. כלומר, אם <math>x_0</math> אי־רציפות אזי <math>\lim\limits_{x\to x_0^+}f(x),\lim\limits_{x\to x_0^-}f(x)</math> קיימים במובן הצר. |
{{פס|{{הערה|הערה: מובן שניתן לדבר גם על פונקציות רציפות למקוטעין בתחומים אחרים, אולם אנו לא נעסוק בהן.}}}} | {{פס|{{הערה|הערה: מובן שניתן לדבר גם על פונקציות רציפות למקוטעין בתחומים אחרים, אולם אנו לא נעסוק בהן.}}}} | ||
| שורה 9: | שורה 9: | ||
#סכום, הפרש או כפל של פונקציות רציפות למקוטעין גם היא רציפה למקוטעין. | #סכום, הפרש או כפל של פונקציות רציפות למקוטעין גם היא רציפה למקוטעין. | ||
#הכפלה של פונקציה רציפה למקוטעין בסקלר היא פונקציה רציפה למקוטעין. | #הכפלה של פונקציה רציפה למקוטעין בסקלר היא פונקציה רציפה למקוטעין. | ||
| − | לפיכך מתקיימים התנאים לתת־מרחב לינארי, כלומר קבוצת הפונקציות הרציפות למקוטעין הוא מרחב לינארי. נסמן מרחב זה ב־<math>E</math>. המכפלה הפנימית בו מוגדרת כ־<math>\langle f,g\rangle=\ | + | לפיכך מתקיימים התנאים לתת־מרחב לינארי, כלומר קבוצת הפונקציות הרציפות למקוטעין הוא מרחב לינארי. נסמן מרחב זה ב־<math>E</math>. המכפלה הפנימית בו מוגדרת כ־<math>\displaystyle\langle f,g\rangle=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\overline{g(x)}dx</math>. |
| − | === משפט === | + | ===משפט=== |
| − | סדרת הפונקציות <math>\left\{\ | + | סדרת הפונקציות <math>\left\{\frac{1}{\sqrt2},\sin(x),\cos(x),\sin(2x),\cos(2x),\ldots\right\}</math> היא מערכת אורתונורמלית ב־<math>E</math>. |
| − | ==== הוכחה ==== | + | ====הוכחה==== |
| − | נראה כי מכפלה פנימית של כל זוג | + | נראה כי מכפלה פנימית של כל זוג אברים שונים במערכת שווה ל־0, ושנורמה של כל אבר היא 1: |
| − | + | :<math>\begin{align}\left\langle\frac{1}{\sqrt2},\sin(nx)\right\rangle&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{1}{\sqrt2}\sin(nx)dx=\left[-\frac{1}{\sqrt2\pi n}\cos(nx)\right]_{-\pi}^\pi=\frac{-1}{\sqrt2\pi n}\Big(\cos(n\pi)-\cos(n\pi)\Big)=0\\\left\langle\frac{1}{\sqrt2},\cos(nx)\right\rangle&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{1}{\sqrt2}\cos(nx)dx=\left[\frac{1}{\sqrt2\pi n}\sin(nx)\right]_{-\pi}^\pi=\frac{1}{\sqrt2\pi n}\Big(\sin(n\pi)-\sin(n\pi)\Big)=0\\\bigl\langle\sin(mx),\cos(nx)\bigr\rangle&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\sin(mx)\cos(nx)dx=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{\sin((n+n)x)+\sin((m-n)x)}{2}dx\\&=-\frac{1}{2\pi}\left[\frac{\cos((m+n)x)}{m+n}+\frac{\cos((m-n)x)}{m-n}\right]_{-\pi}^\pi=0\end{align}</math> | |
| − | הערה: נעזרנו | + | הערה: נעזרנו בזהות <math>\sin(\alpha)\cos(\beta)=\dfrac{\sin(\alpha+\beta)+\sin(\alpha-\beta)}{2}</math>. דרך נוספת תהיה להשתמש פעמיים באינטגרציה בחלקים: |
| − | דרך נוספת תהיה להשתמש פעמיים באינטגרציה בחלקים: <math>\int\sin(mx)\cos(nx) | + | :<math>\int\sin(mx)\cos(nx)dx=\left[\dfrac{n\sin(mx)\sin(nx)-m\cos(mx)\cos(nx)}{1-m^2}\right]_{-\pi}^\pi=0</math> |
| + | עדיף לבדוק לפני ביצוע האינטגרציה אם מדובר בפונקציה זוגית או אי־זוגית. | ||
| − | באותו אופן ניתן להראות | + | באותו אופן ניתן להראות כי <math>\langle\sin(mx),\sin(nx)\rangle=\langle\cos(mx),\cos(nx)\rangle=0</math>. |
| − | עתה נראה | + | עתה נראה שהנורמה של כל אבר היא 1: |
| − | + | :<math>\begin{align}\left\|\frac{1}{\sqrt2}\right\|^2&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{dx}{\sqrt{2}^2}=\frac{2\pi}{2\pi}=1\\\|\sin(nx)\|^2&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\sin(nx)^2dx=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{1-\cos(2nx)}{2}dx=\frac{1}{\pi}\left[\frac{x}{2}-\frac{\sin(2nx)}{4n}\right]_{-\pi}^\pi=1\\\|\cos(nx)\|^2&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\cos(nx)^2dx=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{1+\cos(2nx)}{2}dx=1\end{align}</math> | |
| − | == מערכת סגורה == | + | ==מערכת סגורה== |
| − | '''הגדרה:''' תהי <math>\{\mathbf e_1,\mathbf e_2,\dots\}</math> מערכת אורתונורמלית אינסופית במרחב מ״פ <math>V</math>. המערכת תקרא ''סגורה'' ב־<math>V</math> אם <math>\forall\mathbf u\in V:\ \ | + | '''הגדרה:''' תהי <math>\{\mathbf e_1,\mathbf e_2,\dots\}</math> מערכת אורתונורמלית אינסופית במרחב מ״פ <math>V</math>. המערכת תקרא ''סגורה'' ב־<math>V</math> אם |
| + | :<math>\forall\mathbf u\in V:\ \lim\limits_{n\to\infty}\left\|\mathbf u-\sum\limits_{k=1}^n\langle\mathbf u,\mathbf e_k\rangle\mathbf e_k\right\|=0</math> | ||
| − | '''מסקנה''': ניתן להציג כל <math>f</math> בעזרת צירוף לינארי אינסופי של | + | '''מסקנה''': ניתן להציג כל <math>f</math> בעזרת צירוף לינארי אינסופי של האברים השייכים למערכת האורתונורמלית האינסופית. נמצא את סדרת מקדמי פורייה עבור המערכת האורתונורמלית החדשה שהגדרנו. |
| + | :<math>\begin{align}1.&\mathbf e_1(x)=\frac{1}{\sqrt2}\\&a_0:=\langle f,\mathbf e_1\rangle\mathbf e_1=\left(\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\frac{1}{\sqrt2}dx\right)\frac{1}{\sqrt2}=\frac{1}{2\pi}\int\limits_{-\pi}^\pi f(x)dx\\2.&\mathbf e_n=\sin(nx)\\&\langle f,\mathbf e_n\rangle\mathbf e_n=\underbrace{\left(\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\sin(nx)dx\right)}_{b_n}\sin(nx)\\3.&\mathbf e_n=\cos(nx)\\&\langle f,\mathbf e_n\rangle\mathbf e_n=\underbrace{\left(\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\cos(nx)dx\right)}_{a_n}\cos(nx)\end{align}</math> | ||
| − | + | לסיכום, ניתן לרשום את כל הטור בצורה הבאה: | |
| + | :<math>\frac{a_0}{2}+\sum_{n=1}^\infty\Big(a_n\cos(nx)+b_n\sin(nx)\Big)\\\begin{cases}\displaystyle a_n=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\cos(nx)dx,&n=0,1,2,\ldots\\\displaystyle b_n=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\sin(nx)dx,&n=1,2,\ldots\end{cases}</math> | ||
| − | + | ==טור פורייה== | |
| − | + | תהי <math>f\in E</math>. הטור שמצאנו נקרא טור פורייה של <math>f</math> ויסומן | |
| − | == טור פורייה == | + | :<math>\displaystyle f(x)\sim\dfrac{a_0}{2}+\sum_{n=1}^\infty\Big(a_n\cos(nx)+b_n\sin(nx)\Big)</math> |
| − | תהי <math>f\in E</math>. הטור | + | |
=== פונקציות זוגיות ואי־זוגיות === | === פונקציות זוגיות ואי־זוגיות === | ||
'''תכונות:''' | '''תכונות:''' | ||
| − | * מכפלה של פונקציות זוגיות היא זוגית. | + | *מכפלה של פונקציות זוגיות היא זוגית. |
| − | * מכפלה של פונקציות אי־זוגיות היא זוגית. | + | *מכפלה של פונקציות אי־זוגיות היא זוגית. |
| − | * מכפלה של פונקציה זוגית ופונקציה אי־זוגית היא אי־זוגית. | + | *מכפלה של פונקציה זוגית ופונקציה אי־זוגית היא אי־זוגית. |
| − | ==== משפט ==== | + | ====משפט==== |
תהי <math>f\in E</math>. | תהי <math>f\in E</math>. | ||
| − | * אם <math>f</math> זוגית אז טור פורייה שלה הוא <math>\ | + | *אם <math>f</math> זוגית אז טור פורייה שלה הוא <math>\dfrac{a_0}{2}+\sum\limits_{n=1}^\infty a_n\cos(nx)</math>. טור כזה נקרא "טור קוסינוסים". |
| − | * אם <math>f</math> אי־זוגית אז טור פורייה שלה הוא <math>\ | + | *אם <math>f</math> אי־זוגית אז טור פורייה שלה הוא <math>\sum\limits_{n=1}^\infty b_n\sin(nx)</math>. טור כזה נקרא "טור סינוסים". |
| − | ==== תרגיל ==== | + | ====תרגיל==== |
| − | מצא טור פורייה של <math>f(x)=\begin{cases} | + | מצא טור פורייה של <math>f(x)=\begin{cases}-2&:\!x<0\\1&:\!x\ge0\end{cases}</math> בקטע <math>[-\pi,\pi]</math>. |
| − | ===== פתרון ===== | + | =====פתרון===== |
| − | ראשית, נשים לב שהפונקציה אינה זוגית ואינה אי־זוגית. מתקיים | + | ראשית, נשים לב שהפונקציה אינה זוגית ואינה אי־זוגית. מתקיים |
| − | ולכן <math>f(x)\ | + | :<math>\begin{align}a_0&=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)dx=\frac{1}{\pi}\int\limits_{-\pi}^0 -2\,dx+\frac{1}{\pi}\int\limits_0^\pi dx=\frac{1}{\pi}[-2x]_{-\pi}^0+\frac{1}{\pi}[x]_0^\pi=-2+1=-1\\a_n&=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\cos(nx)dx=0\\b_n&=\frac1\pi\int\limits_{-\pi}^\pi f(x)\sin(nx)dx=\begin{cases}0&:\!n\in2\Z\\\dfrac{6}{\pi n}&:\!n\in2\Z+1\end{cases}\end{align}</math> |
| + | ולכן <math>f(x)\sim-\dfrac12+\sum\limits_{n=1}^\infty\dfrac{6}{(2n-1)\pi}\sin((2n-1)x)</math>. נשים לב שזה עדיין לא טור סינוסים, בגלל האבר <math>-\frac12</math> שבהתחלה. | ||
| − | ==== תרגיל ==== | + | ====תרגיל==== |
מצא טור פורייה של <math>f(x)=x</math> ב־<math>[-\pi,\pi]</math>. | מצא טור פורייה של <math>f(x)=x</math> ב־<math>[-\pi,\pi]</math>. | ||
| − | ===== פתרון ===== | + | =====פתרון===== |
| − | <math>f</math> אי־זוגית ולכן נחשב לה טור סינוסים: <math>b_n=\ | + | <math>f</math> אי־זוגית ולכן נחשב לה טור סינוסים: |
| + | :<math>\begin{align}b_n&=\frac{1}{\pi}\int\limits_{-\pi}^\pi x\sin(nx)dx=\begin{bmatrix}u=x&u'=1\\v'=\sin(nx)&v=-\frac{\cos(nx)}{n}\end{bmatrix}\\&=\frac{2}{\pi}\left[-\frac{x\cos(nx)}{n}\right]_0^\pi+\frac{2}{\pi}\int\limits_0^\pi\frac{\cos(nx)}{n}dx=\frac{2}{\pi}\frac{-\pi(-1)^n}{n}+\frac{2}{\pi}\left[\frac{\sin(nx)}{n^2}\right]_0^\pi=\dfrac{2(-1)^{n+1}}{n}\end{align}</math> | ||
| + | כלומר <math>x\sim\sum\limits_{n=1}^\infty\dfrac{2(-1)^{n+1}}{n}\sin(nx)</math>. | ||
| − | ==== תרגיל ==== | + | ====תרגיל==== |
| − | נתונה <math>f\in E[-\pi,\pi]</math>. לכל <math>a,b,c\in\ | + | נתונה <math>f\in E[-\pi,\pi]</math>. לכל <math>a,b,c\in\C</math> נגדיר |
| + | :<math>G(a,b,c)=\frac{1}{\pi}\int\limits_{-\pi}^\pi|f(x)+a+b\cos(x)+c\sin(x)|dx</math> | ||
| + | עבור אלה ערכי <math>a,b,c</math> מקבלת <math>G</math> את ערכה המינימלי? | ||
| − | ===== פתרון ===== | + | =====פתרון===== |
| − | נשים לב | + | נשים לב כי <math>G(a,b,c)=\Big\|f(x)-{\color{#0000FF}(-a-b\cos(x)-c\sin(x))}\Big\|^2</math>. אם החלק הכחול הוא ההיטל האורתוגונלי של <math>f</math> אזי מובטח לנו כי <math>G(a,b,c)</math> מקבלת את ערכה המינימלי. נפתור זאת: |
| + | :<math>\begin{align}-a&=\frac{\langle f,1\rangle}{\|1\|^2}=\dfrac{\displaystyle\dfrac{1}{\pi}\int\limits_{-\pi}^\pi f(x)dx}{\displaystyle\dfrac{1}{\pi}\int\limits_{-\pi}^\pi dx}=\frac{1}{2\pi}\int\limits_{-\pi}^\pi f(x)dx\\-b&=\frac{\langle f,\cos\rangle}{\|\cos\|^2}=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\cos(x)dx\\-c&=\frac{\langle f,\sin\rangle}{\|\sin\|^2}=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\sin(x)dx\end{align}</math> | ||
---- | ---- | ||
| − | נתייחס למרחב הלינארי <math>\ell_2</math> | + | נתייחס למרחב הלינארי <math>\ell_2</math> ולאבר <math>x=\left\{\dfrac{5^n-3^n}{7^n}\right\}_{n=1}^\infty</math>. מתקיים |
| + | :<math>\displaystyle\|x\|_2^2=\sum_{n=1}^\infty\left(\frac{5^n-3^n}{7^n}\right)^2=\sum_{n=1}^\infty\frac{25^n-2\cdot15^n+9^n}{49^n}=\sum_{n=1}^\infty\left(\frac{25}{49}\right)^n-2\sum_{n=1}^\infty\left(\frac{15}{49}\right)^n+\sum_{n=1}^\infty\left(\frac9{49}\right)^n</math> | ||
| + | אלה טורים הנדסיים והתוצאה היא <math>\frac{16}{85}</math>. לכן <math>\|x\|_2=\frac{4}{\sqrt{85}}</math>. {{משל}} | ||
גרסה אחרונה מ־20:47, 13 בינואר 2021
תוכן עניינים
פונקציה רציפה למקוטעין
הגדרה: הפונקציה ![f:[-\pi,\pi]\to\C](/images/math/5/8/0/5805c5bfab6b88a55541488ad7abbf02.png) תקרא רציפה למקוטעין אם:
תקרא רציפה למקוטעין אם:
- ל־
 יש לכל היותר מספר סופי של נקודות אי־רציפות.
יש לכל היותר מספר סופי של נקודות אי־רציפות. - בכל נקודת אי־רציפות קיימים הגבולות החד־צדדיים. כלומר, אם
 אי־רציפות אזי
אי־רציפות אזי 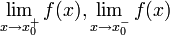 קיימים במובן הצר.
קיימים במובן הצר.
- ל־
הערה: מובן שניתן לדבר גם על פונקציות רציפות למקוטעין בתחומים אחרים, אולם אנו לא נעסוק בהן.
תכונות
- סכום, הפרש או כפל של פונקציות רציפות למקוטעין גם היא רציפה למקוטעין.
- הכפלה של פונקציה רציפה למקוטעין בסקלר היא פונקציה רציפה למקוטעין.
לפיכך מתקיימים התנאים לתת־מרחב לינארי, כלומר קבוצת הפונקציות הרציפות למקוטעין הוא מרחב לינארי. נסמן מרחב זה ב־ . המכפלה הפנימית בו מוגדרת כ־
. המכפלה הפנימית בו מוגדרת כ־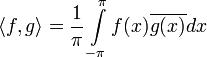 .
.
משפט
סדרת הפונקציות 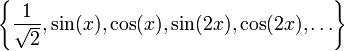 היא מערכת אורתונורמלית ב־
היא מערכת אורתונורמלית ב־ .
.
הוכחה
נראה כי מכפלה פנימית של כל זוג אברים שונים במערכת שווה ל־0, ושנורמה של כל אבר היא 1:
הערה: נעזרנו בזהות 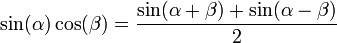 . דרך נוספת תהיה להשתמש פעמיים באינטגרציה בחלקים:
. דרך נוספת תהיה להשתמש פעמיים באינטגרציה בחלקים:
עדיף לבדוק לפני ביצוע האינטגרציה אם מדובר בפונקציה זוגית או אי־זוגית.
באותו אופן ניתן להראות כי 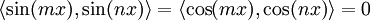 .
.
עתה נראה שהנורמה של כל אבר היא 1:
מערכת סגורה
הגדרה: תהי 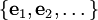 מערכת אורתונורמלית אינסופית במרחב מ״פ
מערכת אורתונורמלית אינסופית במרחב מ״פ  . המערכת תקרא סגורה ב־
. המערכת תקרא סגורה ב־ אם
אם
מסקנה: ניתן להציג כל  בעזרת צירוף לינארי אינסופי של האברים השייכים למערכת האורתונורמלית האינסופית. נמצא את סדרת מקדמי פורייה עבור המערכת האורתונורמלית החדשה שהגדרנו.
בעזרת צירוף לינארי אינסופי של האברים השייכים למערכת האורתונורמלית האינסופית. נמצא את סדרת מקדמי פורייה עבור המערכת האורתונורמלית החדשה שהגדרנו.
לסיכום, ניתן לרשום את כל הטור בצורה הבאה:
- עיבוד הנוסחה נכשל (שגיאת תחביר): \frac{a_0}{2}+\sum_{n=1}^\infty\Big(a_n\cos(nx)+b_n\sin(nx)\Big)\\\begin{cases}\displaystyle a_n=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\cos(nx)dx,&n=0,1,2,\ldots\\\displaystyle b_n=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\sin(nx)dx,&n=1,2,\ldots\end{cases}
טור פורייה
תהי 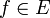 . הטור שמצאנו נקרא טור פורייה של
. הטור שמצאנו נקרא טור פורייה של  ויסומן
ויסומן
פונקציות זוגיות ואי־זוגיות
תכונות:
- מכפלה של פונקציות זוגיות היא זוגית.
- מכפלה של פונקציות אי־זוגיות היא זוגית.
- מכפלה של פונקציה זוגית ופונקציה אי־זוגית היא אי־זוגית.
משפט
תהי 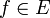 .
.
- אם
 זוגית אז טור פורייה שלה הוא
זוגית אז טור פורייה שלה הוא 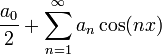 . טור כזה נקרא "טור קוסינוסים".
. טור כזה נקרא "טור קוסינוסים". - אם
 אי־זוגית אז טור פורייה שלה הוא
אי־זוגית אז טור פורייה שלה הוא 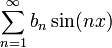 . טור כזה נקרא "טור סינוסים".
. טור כזה נקרא "טור סינוסים".
תרגיל
מצא טור פורייה של 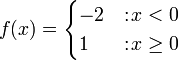 בקטע
בקטע ![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) .
.
פתרון
ראשית, נשים לב שהפונקציה אינה זוגית ואינה אי־זוגית. מתקיים
ולכן 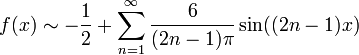 . נשים לב שזה עדיין לא טור סינוסים, בגלל האבר
. נשים לב שזה עדיין לא טור סינוסים, בגלל האבר 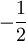 שבהתחלה.
שבהתחלה.
תרגיל
מצא טור פורייה של 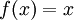 ב־
ב־![[-\pi,\pi]](/images/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) .
.
פתרון
 אי־זוגית ולכן נחשב לה טור סינוסים:
אי־זוגית ולכן נחשב לה טור סינוסים:
כלומר 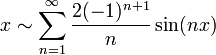 .
.
תרגיל
נתונה ![f\in E[-\pi,\pi]](/images/math/7/7/b/77b18dfe592c7b301f00b6c5fac4b4cc.png) . לכל
. לכל 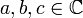 נגדיר
נגדיר
עבור אלה ערכי 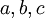 מקבלת
מקבלת 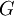 את ערכה המינימלי?
את ערכה המינימלי?
פתרון
נשים לב כי עיבוד הנוסחה נכשל (שגיאת לקסינג): G(a,b,c)=\Big\|f(x)-{\color{#0000FF}(-a-b\cos(x)-c\sin(x))}\Big\|^2
. אם החלק הכחול הוא ההיטל האורתוגונלי של  אזי מובטח לנו כי
אזי מובטח לנו כי 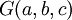 מקבלת את ערכה המינימלי. נפתור זאת:
מקבלת את ערכה המינימלי. נפתור זאת:
נתייחס למרחב הלינארי 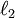 ולאבר
ולאבר 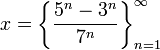 . מתקיים
. מתקיים
אלה טורים הנדסיים והתוצאה היא 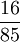 . לכן
. לכן 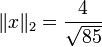 .
. 
![\begin{align}\left\langle\frac{1}{\sqrt2},\sin(nx)\right\rangle&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{1}{\sqrt2}\sin(nx)dx=\left[-\frac{1}{\sqrt2\pi n}\cos(nx)\right]_{-\pi}^\pi=\frac{-1}{\sqrt2\pi n}\Big(\cos(n\pi)-\cos(n\pi)\Big)=0\\\left\langle\frac{1}{\sqrt2},\cos(nx)\right\rangle&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{1}{\sqrt2}\cos(nx)dx=\left[\frac{1}{\sqrt2\pi n}\sin(nx)\right]_{-\pi}^\pi=\frac{1}{\sqrt2\pi n}\Big(\sin(n\pi)-\sin(n\pi)\Big)=0\\\bigl\langle\sin(mx),\cos(nx)\bigr\rangle&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\sin(mx)\cos(nx)dx=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{\sin((n+n)x)+\sin((m-n)x)}{2}dx\\&=-\frac{1}{2\pi}\left[\frac{\cos((m+n)x)}{m+n}+\frac{\cos((m-n)x)}{m-n}\right]_{-\pi}^\pi=0\end{align}](/images/math/0/0/9/009ff687c3a5263c6c1b6f4de3b90c29.png)
![\int\sin(mx)\cos(nx)dx=\left[\dfrac{n\sin(mx)\sin(nx)-m\cos(mx)\cos(nx)}{1-m^2}\right]_{-\pi}^\pi=0](/images/math/a/f/7/af7308f2711c83762680629cc30cfeae.png)
![\begin{align}\left\|\frac{1}{\sqrt2}\right\|^2&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{dx}{\sqrt{2}^2}=\frac{2\pi}{2\pi}=1\\\|\sin(nx)\|^2&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\sin(nx)^2dx=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{1-\cos(2nx)}{2}dx=\frac{1}{\pi}\left[\frac{x}{2}-\frac{\sin(2nx)}{4n}\right]_{-\pi}^\pi=1\\\|\cos(nx)\|^2&=\frac{1}{\pi}\int\limits_{-\pi}^\pi\cos(nx)^2dx=\frac{1}{\pi}\int\limits_{-\pi}^\pi\frac{1+\cos(2nx)}{2}dx=1\end{align}](/images/math/d/c/0/dc0953f13573fa9640c779e5f9db521b.png)
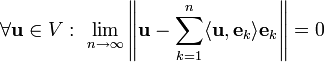
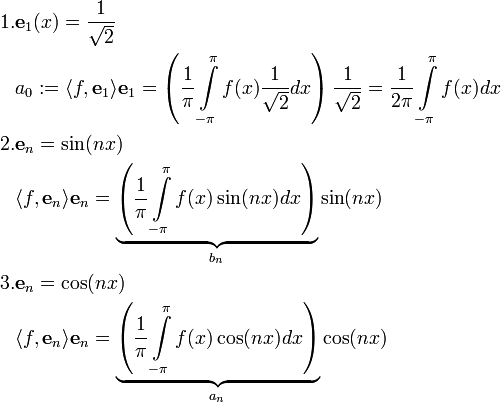
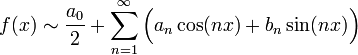
![\begin{align}a_0&=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)dx=\frac{1}{\pi}\int\limits_{-\pi}^0 -2\,dx+\frac{1}{\pi}\int\limits_0^\pi dx=\frac{1}{\pi}[-2x]_{-\pi}^0+\frac{1}{\pi}[x]_0^\pi=-2+1=-1\\a_n&=\frac{1}{\pi}\int\limits_{-\pi}^\pi f(x)\cos(nx)dx=0\\b_n&=\frac1\pi\int\limits_{-\pi}^\pi f(x)\sin(nx)dx=\begin{cases}0&:\!n\in2\Z\\\dfrac{6}{\pi n}&:\!n\in2\Z+1\end{cases}\end{align}](/images/math/f/c/3/fc361b3fe8bcd5bf504f0e6981a89a5b.png)
![\begin{align}b_n&=\frac{1}{\pi}\int\limits_{-\pi}^\pi x\sin(nx)dx=\begin{bmatrix}u=x&u'=1\\v'=\sin(nx)&v=-\frac{\cos(nx)}{n}\end{bmatrix}\\&=\frac{2}{\pi}\left[-\frac{x\cos(nx)}{n}\right]_0^\pi+\frac{2}{\pi}\int\limits_0^\pi\frac{\cos(nx)}{n}dx=\frac{2}{\pi}\frac{-\pi(-1)^n}{n}+\frac{2}{\pi}\left[\frac{\sin(nx)}{n^2}\right]_0^\pi=\dfrac{2(-1)^{n+1}}{n}\end{align}](/images/math/0/7/1/07166699fc6bdf73e53473253938c1c9.png)