הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - תרגול/6.3.11"
מתוך Math-Wiki
< משתמש:אור שחף | 133 - תרגול
(יצירת דף עם התוכן "==שיטות פרמיטיביות לחישוב שטחים== '''המטרה:''' לחשב שטח מתחת לכל עקומה (כמעט). ==דוגמה 1== חשב את ...") |
(←דוגמה 1 {{הערה|(שיטת פירוק)}}) |
||
| (5 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | + | =שיטות פרמיטיביות לחישוב שטחים= | |
'''המטרה:''' לחשב שטח מתחת לכל עקומה (כמעט). | '''המטרה:''' לחשב שטח מתחת לכל עקומה (כמעט). | ||
| שורה 5: | שורה 5: | ||
חשב את השטח הכלוא בין ציר ה-x לעקומה במקרים הבאים: | חשב את השטח הכלוא בין ציר ה-x לעקומה במקרים הבאים: | ||
| − | # <math>\int\limits_0^5 |x-3|\mathrm dx</math><br/> פתרון: נשים לב להגדרת <math>|x-3|</math> לפיה האינטגרל שווה ל-<math>\int\limits_0^3-(x-3)\mathrm dx+\int\limits_3^5 (x-3)\mathrm dx</math>. מספיק לחשב את השטחים I ו-II. נעשה זאת לפי שטח משולש: עבור I - <math>\int\limits_0^3-(x-3)\mathrm dx=\frac{3\cdot3}2=4.5</math> ועבור II - <math>\int\limits_3^5 (x-3)\mathrm dx=\frac{2\cdot2}2=2</math> ולכן השטח הכולל הוא 6.5. | + | # <math>\int\limits_0^5 |x-3|\mathrm dx</math><br/> פתרון: נשים לב להגדרת <math>|x-3|</math> לפיה האינטגרל שווה ל-<math>\int\limits_0^3-(x-3)\mathrm dx+\int\limits_3^5 (x-3)\mathrm dx</math>. גרף (1) מספיק לחשב את השטחים I ו-II. נעשה זאת לפי שטח משולש: עבור I - <math>\int\limits_0^3-(x-3)\mathrm dx=\frac{3\cdot3}2=4.5</math> ועבור II - <math>\int\limits_3^5 (x-3)\mathrm dx=\frac{2\cdot2}2=2</math> ולכן השטח הכולל הוא 6.5. {{משל}}<br />''הערה:'' אם התחום היה, למשל, <math>[4,5]</math> היינו יכולים לחשב לפי שטח טרפז. |
| − | + | # <math>\int\limits_0^{10} \sqrt{10x-x^2}\mathrm dx</math>. פתרון: נבדוק מהו גרף הפונקציה. נסמן <math>y=\sqrt{10x-x^2}\implies y^2=10x-x^2\implies (x-5)^2+y^2=5^2</math>. קיבלנו מעגל - גרף (2). מסימטריות המעגל אפשר לקחת חצי משטח המעגל. <math>\int\limits_0^{10}\sqrt{10x-x^2}\mathrm dx=\frac{25\pi}2</math> {{משל}} | |
| − | # <math>\int\limits_0^{10} \sqrt{10x-x^2}\mathrm dx</math>. פתרון: נבדוק מהו גרף הפונקציה. נסמן <math>y=\sqrt{10x-x^2}\implies y^2=10x-x^2\implies (x-5)^2+y^2=5^2</math>. קיבלנו מעגל - גרף (2). מסימטריות המעגל אפשר לקחת חצי משטח המעגל. <math>\int\limits_0^{10}\sqrt{10x-x^2}\mathrm dx=\frac{25\pi}2 | + | # <math>\int\limits_a^b\sqrt\frac{4-x^2}2\mathrm dx</math>, כאשר a,b הם גבולות העקומה. פתרון: נסמן <math>y=\sqrt\frac{4-x^2}2\implies \left(\frac y\sqrt2\right)^2+\left(\frac x2\right)^2=0</math>. זוהי אליפסה שמרכזה ב-<math>(0,0)</math>. נסמן <math>a=2,\ b=\sqrt2</math> ולפי נוסחה לשטח אליפסה (<math>\pi a b</math>) נקבל <math>2\sqrt2\pi</math>. האינטגרל הוא מחצית השטח, כלומר <math>\sqrt2\pi</math>. {{משל}} |
| − | # <math>\int\limits_a^b\sqrt\frac{4-x^2}2\mathrm dx</math>, כאשר a,b הם גבולות העקומה. פתרון: נסמן <math>y=\sqrt\frac{4-x^2}2\implies \left(\frac y\sqrt2\right)^2+\left(\frac x2\right)^2</math>. זוהי אליפסה שמרכזה ב-<math>(0,0)</math>. נסמן <math>a=2,\ b=\sqrt2</math> ולפי נוסחה לשטח אליפסה (<math>\pi a b</math>) נקבל <math>2\sqrt2\pi</math> | + | |
=האינטגרל הלא מסויים= | =האינטגרל הלא מסויים= | ||
| − | '''המטרה:''' להגדיר אינטגרל דרך פונקציה קדומה | + | '''המטרה:''' להגדיר אינטגרל דרך פונקציה קדומה: <math>F(x)=\int f(x)\mathrm dx</math> ולכן אפשר להשתמש בכיוון השני של טבלת הגזירה. למשל, <math>\frac{\mathrm d\ln(x)}{\mathrm dx}=\frac1x</math> ולכן <math>\int\frac{\mathrm dx}x=\ln|x|+c</math> |
==דוגמה 1 {{הערה|(שיטת פירוק)}}== | ==דוגמה 1 {{הערה|(שיטת פירוק)}}== | ||
חשב <math>\int\frac{2x^4}{1+x^2}\mathrm dx</math>. | חשב <math>\int\frac{2x^4}{1+x^2}\mathrm dx</math>. | ||
===פתרון=== | ===פתרון=== | ||
| − | זה שווה ל-<math>2\int\frac{x^4+1-1}{1+x^2}\mathrm dx=2\int(x^2-1)\mathrm dx+2\int\frac{\mathrm dx}{1+x^2}=2\frac{x^3}3-2x+2\arcsin(x)+c</math> | + | זה שווה ל-{{left|<math>\begin{align}2\int\frac{x^4-1+1}{1+x^2}\mathrm dx&=2\int\left(\frac{(x^2-1)(x^2+1)}{x^2+1}+\frac1{x^2+1}\right)\mathrm dx\\&=2\int(x^2-1)\mathrm dx+2\int\frac{\mathrm dx}{1+x^2}\\&=2\frac{x^3}3-2x+2\arcsin(x)+c\end{align}</math>}} |
| + | {{משל}} | ||
| + | '''באופן כללי:''' נבדוק מה מאפס את המונה ומה מאפס את המכנה (במקרה הזה לא מתאפס ב-<math>\mathbb R</math>). אם מצטמצם ננסה חילוק פולינומים, אחרת נחפש להציג כקבוע ועוד שארית. דוגמה נוספת: <math>\int\frac{x^2}{x^2+1}\mathrm dx=\int\frac{x^2+1-1}{x^2+1}\mathrm dx</math>. | ||
| − | + | ==דוגמה 2== | |
| + | חשב <math>I=\int\frac{\mathrm dx}{\sin^2(x)\cos^2(x)}</math>. | ||
| + | ===פתרון=== | ||
| + | '''דרך א:''' מתקיים <math>I=4\int\frac{\mathrm dx}{\Big(2\sin(x)\cos(x)\Big)^2}=4\int\frac{\mathrm dx}{(\sin(2x))^2}</math>. זהו אינטגרל לא פשוט ולכן ננסה את '''דרך ב:''' {{left|<math>\begin{align}I&=\int\frac{\sin^2(x)+\cos^2(x)}{\sin^2(x)\cos^2(x)}\mathrm dx\\&=\int\frac{\mathrm dx}{\sin^2(x)}+\int\frac{\mathrm dx}{\cos^2(x)}\\&=\tan(x)-\cot(x)+c\end{align}</math>}} | ||
| + | {{משל}} | ||
| − | + | ניתן לבדוק זאת ע"י גזירת הפונקציה הקדומה, אבל כמובן שההוכחה הזו מספיקה. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
---- | ---- | ||
| שורה 32: | שורה 32: | ||
'''שיטת ההצבה:''' <math>\int f(g(x))g'(x)\mathrm dx=F(g(x))+c</math> | '''שיטת ההצבה:''' <math>\int f(g(x))g'(x)\mathrm dx=F(g(x))+c</math> | ||
| − | + | ==דוגמה 3== | |
חשב <math>\int\sin^5(x)\cos(x)\mathrm dx</math>. | חשב <math>\int\sin^5(x)\cos(x)\mathrm dx</math>. | ||
| − | + | ===פתרון=== | |
| − | נציב <math>y=\sin(x)</math> ולכן <math>\mathrm dy=\cos(x)\mathrm dx</math>. | + | נציב <math>y=\sin(x)</math> ולכן <math>\mathrm dy=\cos(x)\mathrm dx</math>. אזי האינטגרל הוא: <math>\int y^5\mathrm dy=\frac{y^6}6+c=\frac{\sin^6(x)}6+c</math>. {{משל}} |
| − | באופן כללי: בפונקציות מהצורה <math>\sin^n(x)\cos^m(x)</math> (עבור <math>n,m\in\mathbb N</math>) נשתמש בשיטת ההצבה אם <math> | + | <!-- |
| − | <math>\sin^2(x)=\frac{1-\cos( | + | '''באופן כללי:''' בפונקציות מהצורה <math>\sin^n(x)\cos^m(x)</math> (עבור <math>n,m\in\mathbb N</math>) נשתמש בשיטת ההצבה אם <math>n</math> אי זוגי, באופן הבא: נציב <math>y=\sin^\frac{n+1}2(x)</math> ואז <math>\mathrm dy=\frac{n+1}2\sin^\frac{n-1}2(x)\cos(x)\mathrm dx</math> ולכן <math>\sin^n(x)\cos^m(x)\mathrm dx=\frac2{n+1}\cos^{m-1}(x)\cdot\frac{n+1}2\cdot\sin^\frac{n+1}2(x)\sin^\frac{n-1}2(x)\cos(x)\mathrm dx=\frac2{n+1}y</math>. |
| − | + | אם <math>n+m</math> זוגי ננסה להשתמש בזהויות השונות, כמו | |
| + | <math>\sin^2(x)=\frac{1-\cos(2x)}2</math>. | ||
| + | --> | ||
| − | ===דוגמה 4 | + | ---- |
| + | |||
| + | '''אינטגרציה בחלקים:''' <math>\int f(x)g'(x)\mathrm dx=f(x)g(x)-\int f'(x)g(x)\mathrm dx</math>. | ||
| + | |||
| + | ==דוגמה 4== | ||
חשב את האינטגרלים הבאים: | חשב את האינטגרלים הבאים: | ||
| − | + | <ol> | |
| − | + | <li><math>\int xe^x\mathrm dx</math> | |
| − | + | ===פתרון=== | |
| + | לפי אינטגרציה בחלקים, נגדיר <math>f(x)=x\ \and\ g(x)=e^x</math>. לכן האינטגרל שווה ל-<math>xe^x-\int1e^x\mathrm dx=xe^x-e^x+c</math>. {{משל}} | ||
| + | |||
| + | '''מסקנה:''' לכל פולינום ממעלה <math>n\in\mathbb N</math> כפול פונקציה g שמקיימת (עבור <math>m\in\mathbb N</math> כלשהו) <math>g^{(m)}(x)=g(x)</math> נעשה אינטגרציה בחלקים n פעמים ונקבל את הפתרון<!--: {{left|<math>\begin{align}\int g(x)\sum_{k=0}^n a_kx^k\mathrm dx&=g^{(m-1)}(x)\sum_{k=0}^n a_kx^k-\int g^{(m-1)}(x)\sum_{k=1}^n a_k\cdot kx^{k-1}\mathrm dx\\&=\dots\\&=\sum_{i=0}^{n-1}(-1)^i g^{(m-i-1)}(x)\sum_{k=i}^n a_k \frac{k!}{(k-i)!}x^{k-i}+(-1)^n\int g^{(m-n)}(x)\mathrm dx\\&=\sum_{i=0}^n(-1)^i g^{(m-i-1)}(x)\sum_{k=i}^n a_k \frac{k!}{(k-i)!}x^{k-i}+c\end{align}</math>}}--></li> | ||
| + | <li><math>\int\ln(x)\mathrm dx</math> | ||
| + | ===פתרון=== | ||
| + | נסמן <math>f(x)=\ln(x)\ \and\ g(x)=x</math> ואז <math>x\ln(x)-\int\frac{\mathrm dx}x=x\ln(x)-x+c</math>. {{משל}}</li> | ||
| + | <li><math>\int\sin(x)e^x\mathrm dx</math> | ||
| + | ===פתרון=== | ||
| + | <math>f(x)=\sin(x)\ \and\ g(x)=e^x</math> ואז <math>\sin(x)e^x-\int\cos(x)e^x\mathrm dx</math>. ולפי אינטגרציה שנייה: <math>\sin(x)e^x-\cos(x)e^x-\int\sin(x)e^x\mathrm dx</math> ולכן <math>\int\sin(x)e^x\mathrm dx=\frac12\left(\sin(x)e^x-\cos(x)e^x\right)+c</math>. {{משל}} | ||
| − | מסקנה: במקרה של f,g יש מספר סופי של נגזרות שונות, | + | '''מסקנה:''' במקרה של-f,g יש מספר סופי של נגזרות שונות, נשתמש בשיטה זו.</li> |
| + | </ol> | ||
==דוגמה 5== | ==דוגמה 5== | ||
<math>\int\frac{3^x}\sqrt{1-9^x}\mathrm dx</math>. | <math>\int\frac{3^x}\sqrt{1-9^x}\mathrm dx</math>. | ||
===פתרון=== | ===פתרון=== | ||
| − | בשיטת ההצבה, <math>y=3^x</math> והאינטגרל הנ"ל שווה ל-<math>\frac1{\ln(3)}\int\frac{\mathrm dy}\sqrt{1-y^2}=\frac1{\ln(3)}\arcsin(3^x)+c</math> | + | בשיטת ההצבה, <math>y=3^x\implies\mathrm dy=\ln(3)\cdot3^x\mathrm dx</math> והאינטגרל הנ"ל שווה ל-<math>\frac1{\ln(3)}\int\frac{\mathrm dy}\sqrt{1-y^2}=\frac1{\ln(3)}\arcsin(3^x)+c</math>. {{משל}} |
גרסה אחרונה מ־11:28, 14 במאי 2011
תוכן עניינים
שיטות פרמיטיביות לחישוב שטחים
המטרה: לחשב שטח מתחת לכל עקומה (כמעט).
דוגמה 1
חשב את השטח הכלוא בין ציר ה-x לעקומה במקרים הבאים:
-
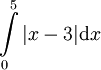
פתרון: נשים לב להגדרת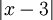 לפיה האינטגרל שווה ל-
לפיה האינטגרל שווה ל-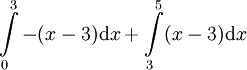 . גרף (1) מספיק לחשב את השטחים I ו-II. נעשה זאת לפי שטח משולש: עבור I -
. גרף (1) מספיק לחשב את השטחים I ו-II. נעשה זאת לפי שטח משולש: עבור I - 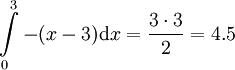 ועבור II -
ועבור II - 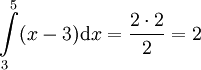 ולכן השטח הכולל הוא 6.5.
ולכן השטח הכולל הוא 6.5. 
הערה: אם התחום היה, למשל,![[4,5]](/images/math/3/0/e/30eeb203d66f0c29522e851b605d8a9e.png) היינו יכולים לחשב לפי שטח טרפז.
היינו יכולים לחשב לפי שטח טרפז. -
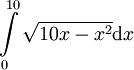 . פתרון: נבדוק מהו גרף הפונקציה. נסמן
. פתרון: נבדוק מהו גרף הפונקציה. נסמן 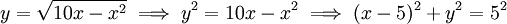 . קיבלנו מעגל - גרף (2). מסימטריות המעגל אפשר לקחת חצי משטח המעגל.
. קיבלנו מעגל - גרף (2). מסימטריות המעגל אפשר לקחת חצי משטח המעגל. 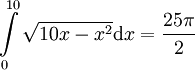

-
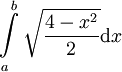 , כאשר a,b הם גבולות העקומה. פתרון: נסמן
, כאשר a,b הם גבולות העקומה. פתרון: נסמן 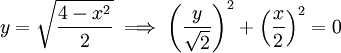 . זוהי אליפסה שמרכזה ב-
. זוהי אליפסה שמרכזה ב-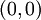 . נסמן
. נסמן 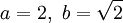 ולפי נוסחה לשטח אליפסה (
ולפי נוסחה לשטח אליפסה (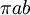 ) נקבל
) נקבל 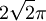 . האינטגרל הוא מחצית השטח, כלומר
. האינטגרל הוא מחצית השטח, כלומר 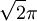 .
. 
האינטגרל הלא מסויים
המטרה: להגדיר אינטגרל דרך פונקציה קדומה: 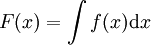 ולכן אפשר להשתמש בכיוון השני של טבלת הגזירה. למשל,
ולכן אפשר להשתמש בכיוון השני של טבלת הגזירה. למשל, 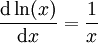 ולכן
ולכן 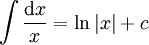
דוגמה 1 (שיטת פירוק)
חשב 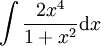 .
.
פתרון
זה שווה ל-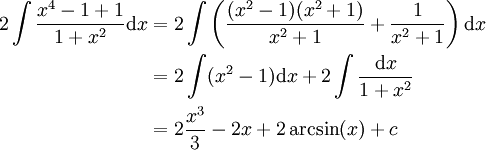

באופן כללי: נבדוק מה מאפס את המונה ומה מאפס את המכנה (במקרה הזה לא מתאפס ב-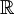 ). אם מצטמצם ננסה חילוק פולינומים, אחרת נחפש להציג כקבוע ועוד שארית. דוגמה נוספת:
). אם מצטמצם ננסה חילוק פולינומים, אחרת נחפש להציג כקבוע ועוד שארית. דוגמה נוספת: 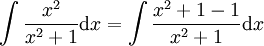 .
.
דוגמה 2
חשב 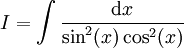 .
.
פתרון
דרך א: מתקיים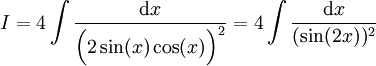 . זהו אינטגרל לא פשוט ולכן ננסה את דרך ב:
. זהו אינטגרל לא פשוט ולכן ננסה את דרך ב: 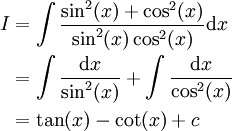

ניתן לבדוק זאת ע"י גזירת הפונקציה הקדומה, אבל כמובן שההוכחה הזו מספיקה.
שיטת ההצבה: 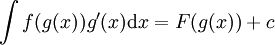
דוגמה 3
חשב 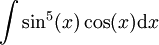 .
.
פתרון
נציב 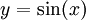 ולכן
ולכן 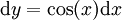 . אזי האינטגרל הוא:
. אזי האינטגרל הוא: 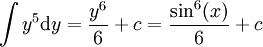 .
. 
אינטגרציה בחלקים: 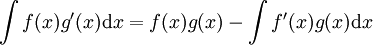 .
.
דוגמה 4
חשב את האינטגרלים הבאים:
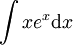
פתרון
לפי אינטגרציה בחלקים, נגדיר
מסקנה: לכל פולינום ממעלה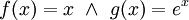 . לכן האינטגרל שווה ל-
. לכן האינטגרל שווה ל-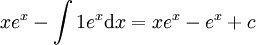 .
. 
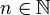 כפול פונקציה g שמקיימת (עבור
כפול פונקציה g שמקיימת (עבור 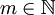 כלשהו)
כלשהו) 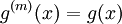 נעשה אינטגרציה בחלקים n פעמים ונקבל את הפתרון
נעשה אינטגרציה בחלקים n פעמים ונקבל את הפתרון
פתרון
נסמן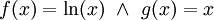 ואז
ואז 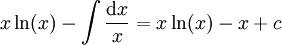 .
. 
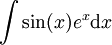
פתרון
מסקנה: במקרה של-f,g יש מספר סופי של נגזרות שונות, נשתמש בשיטה זו.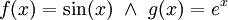 ואז
ואז 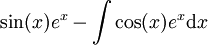 . ולפי אינטגרציה שנייה:
. ולפי אינטגרציה שנייה: 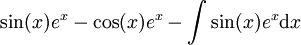 ולכן
ולכן 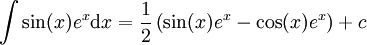 .
. 
דוגמה 5
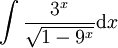 .
.
פתרון
בשיטת ההצבה, 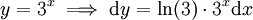 והאינטגרל הנ"ל שווה ל-
והאינטגרל הנ"ל שווה ל-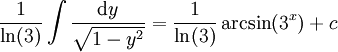 .
. 