הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - שונות/רשימת הגדרות"
מתוך Math-Wiki
< משתמש:אור שחף | 133 - שונות
(המשך יבוא) |
מ (←אינטגרלים) |
||
| שורה 20: | שורה 20: | ||
::* <math>f</math> תקרא '''אינטגרבילית''' (לפי רימן) בקטע אם כאשר <math>\lambda(P)\to0</math> כל סכומי רימן <math>S(f,P,P')</math> שואפים לאותו גבול. | ::* <math>f</math> תקרא '''אינטגרבילית''' (לפי רימן) בקטע אם כאשר <math>\lambda(P)\to0</math> כל סכומי רימן <math>S(f,P,P')</math> שואפים לאותו גבול. | ||
::* עבור f אינטגרבילית (לפי רימן) ב-<math>[a,b]</math> '''האינטגרל המסויים של <math>f</math> בקטע''' (לפי רימן) הוא <math>\int\limits_a^b f:=\lim_{\lambda(P)\to0}S(f,P,P')</math> לכל החלוקות <math>P</math> ו-<math>P'</math>. | ::* עבור f אינטגרבילית (לפי רימן) ב-<math>[a,b]</math> '''האינטגרל המסויים של <math>f</math> בקטע''' (לפי רימן) הוא <math>\int\limits_a^b f:=\lim_{\lambda(P)\to0}S(f,P,P')</math> לכל החלוקות <math>P</math> ו-<math>P'</math>. | ||
| − | ::* אם <math>f(x)\ge0</math> ורציפה ב-<math>[a,b]</math> אז נגדיר את '''השטח שמתחת לגרף''' כ-<math>\int\limits_a^b f</math>. בפרט, לכל < math>f</math> רציפה ב-<math>[a,b]</math> '''השטח שבין הגרף לציר ה-<math>x</math>''' הוא <math>\int\limits_a^b |f|</math>. | + | ::* אם <math>f(x)\ge0</math> ורציפה ב-<math>[a,b]</math> אז נגדיר את '''השטח שמתחת לגרף''' כ-<math>\int\limits_a^b f</math>. בפרט, לכל <math>f</math> רציפה ב-<math>[a,b]</math> '''השטח שבין הגרף לציר ה-<math>x</math>''' הוא <math>\int\limits_a^b |f|</math>. |
:* <math>\int\limits_a^a f:=0</math>. | :* <math>\int\limits_a^a f:=0</math>. | ||
:* אם f אינטגרבילית בקטע אז <math>\int\limits_b^a f:=-\int\limits_a^b f</math>. | :* אם f אינטגרבילית בקטע אז <math>\int\limits_b^a f:=-\int\limits_a^b f</math>. | ||
* פונקציה <math>f</math> תקרא '''רציפה למקוטעין''' בקטע אם היא רציפה בו למעט מספר סופי של נקודות אי רציפות ממין ראשון. | * פונקציה <math>f</math> תקרא '''רציפה למקוטעין''' בקטע אם היא רציפה בו למעט מספר סופי של נקודות אי רציפות ממין ראשון. | ||
* | * | ||
גרסה אחרונה מ־12:29, 7 באפריל 2011
אינטגרלים
- תהי
 מוגדרת בקטע
מוגדרת בקטע 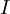 . הפונקציה
. הפונקציה 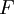 קדומה ל-
קדומה ל- ב-
ב-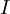 אם
אם 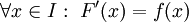 .
.
- תהי
 מוגדרת וחסומה בקטע
מוגדרת וחסומה בקטע 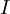 . אזי:
. אזי:
- נסמן את האינפימום של
 כ-
כ-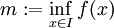 ואת הסופרימום כ-
ואת הסופרימום כ-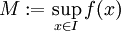 .
. - התנודה של
 היא
היא 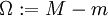 .
. - חלוקה של קטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) היא קבוצה מהצורה
היא קבוצה מהצורה 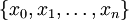 כאשר
כאשר 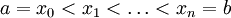 .
.
- עבור חלוקה
 כזו נגדיר:
כזו נגדיר:
- לכל
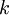 אורך תת הקטע
אורך תת הקטע 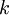 הוא
הוא 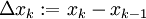 .
. - פרמטר החלוקה הוא
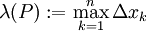 .
. - לכל
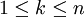 נגדיר
נגדיר ![M_k:=\sup_{x\in[x_{k-1},x_k]}f(x)](/images/math/6/1/5/61578e0c2a9b70125ba8a0e47958631d.png) וכן
וכן ![m_k:=\inf_{x\in[x_{k-1},x_k]}f(x)](/images/math/0/5/2/05215025c0de90c707fecf23537767f9.png) .
. - העדנה
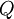 של
של  היא חלוקה של
היא חלוקה של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-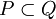 .
. - הסכום העליון הוא
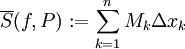 .
. - הסכום התחתון הוא
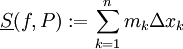 .
. - האינטגרל העליון הוא
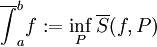 .
. - האינטגרל התחתון הוא
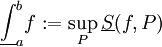 .
. -
 תקרא אינטגרבילית (לפי דרבו) בקטע אם
תקרא אינטגרבילית (לפי דרבו) בקטע אם 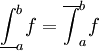 .
. - עבור f אינטגרבילית ב-
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) האינטגרל המסויים של
האינטגרל המסויים של  בקטע (לפי דרבו) הוא
בקטע (לפי דרבו) הוא 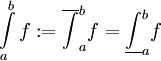 .
. - לכל
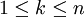 נבחר
נבחר ![c_k\in[x_{k-1},x_k]](/images/math/c/b/b/cbbb2a7a61cd7e98c21895f0cabd6417.png) כך ש-
כך ש-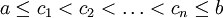 , ונסמן
, ונסמן 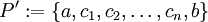 . סכום רימן מוגדר כ-
. סכום רימן מוגדר כ- .
. -
 תקרא אינטגרבילית (לפי רימן) בקטע אם כאשר
תקרא אינטגרבילית (לפי רימן) בקטע אם כאשר 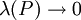 כל סכומי רימן
כל סכומי רימן 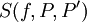 שואפים לאותו גבול.
שואפים לאותו גבול. - עבור f אינטגרבילית (לפי רימן) ב-
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) האינטגרל המסויים של
האינטגרל המסויים של  בקטע (לפי רימן) הוא
בקטע (לפי רימן) הוא  לכל החלוקות
לכל החלוקות  ו-
ו-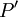 .
. - אם
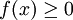 ורציפה ב-
ורציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז נגדיר את השטח שמתחת לגרף כ-
אז נגדיר את השטח שמתחת לגרף כ-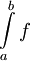 . בפרט, לכל
. בפרט, לכל  רציפה ב-
רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) השטח שבין הגרף לציר ה-
השטח שבין הגרף לציר ה- הוא
הוא 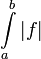 .
.
- לכל
-
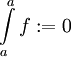 .
. - אם f אינטגרבילית בקטע אז
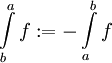 .
.
- נסמן את האינפימום של
- פונקציה
 תקרא רציפה למקוטעין בקטע אם היא רציפה בו למעט מספר סופי של נקודות אי רציפות ממין ראשון.
תקרא רציפה למקוטעין בקטע אם היא רציפה בו למעט מספר סופי של נקודות אי רציפות ממין ראשון.