הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - תרגול/27.3.11"
מתוך Math-Wiki
< משתמש:אור שחף | 133 - תרגול
(←פתרון) |
|||
| שורה 40: | שורה 40: | ||
נציב <math>y=\sqrt{x+2}\implies\mathrm dx=2y\mathrm dy</math> לפיכך <math>\int=\int\frac{2y}{y\left(y^2-4\right)}\mathrm dy=\dots</math>. {{משל}} | נציב <math>y=\sqrt{x+2}\implies\mathrm dx=2y\mathrm dy</math> לפיכך <math>\int=\int\frac{2y}{y\left(y^2-4\right)}\mathrm dy=\dots</math>. {{משל}} | ||
| − | ''' | + | '''מסקנה''': כאשר יש ביטוי מהצורה <math>\sqrt[n]{ax+b}</math> ננסה להציב <math>y^n=ax+b</math>.</li> |
</ol> | </ol> | ||
| שורה 46: | שורה 46: | ||
אם יש ביטוי מהצורה <math>\sqrt{c+bx+x^2}</math> כאשר הפולינום אי פריק נציב <math>(y-x)^2=c+bx+x^2</math>. אם הפולינום בשורש כן פריק ושורשיו <math>\alpha,\ \beta</math> נציב <math>c+bx+x^2=(\beta-y)^2</math> או <math>c+bx+x^2=(\alpha-y)^2</math>. | אם יש ביטוי מהצורה <math>\sqrt{c+bx+x^2}</math> כאשר הפולינום אי פריק נציב <math>(y-x)^2=c+bx+x^2</math>. אם הפולינום בשורש כן פריק ושורשיו <math>\alpha,\ \beta</math> נציב <math>c+bx+x^2=(\beta-y)^2</math> או <math>c+bx+x^2=(\alpha-y)^2</math>. | ||
| + | |||
===דוגמה 4=== | ===דוגמה 4=== | ||
נחשב <math>\int\frac{\mathrm dx}{x\sqrt{x^2+x+2}}</math> | נחשב <math>\int\frac{\mathrm dx}{x\sqrt{x^2+x+2}}</math> | ||
====פתרון==== | ====פתרון==== | ||
הפולינום שבשורש אי פריק, לכן נגדיר y עבורו {{left|<math>\begin{align}&(y-x)^2=x^2+x+2\\\implies&y=x+\sqrt{x^2+x+2}\ \and\ x=\frac{y^2-2}{1+2y}\\\implies&\mathrm dx=\dots=\frac{2(y^2+y+2)}{(1+2y)^2}\mathrm dy\end{align}</math>}}ואז <math>\int=\frac{\frac{2(y^2+y+2)}{(1+2y)^2}\mathrm dy}{\frac{y^2-2}{1+2y}\frac{y^2+y+2}{1+2y}}=2\int\frac{\mathrm dy}{y^2-2}</math>. {{משל}} | הפולינום שבשורש אי פריק, לכן נגדיר y עבורו {{left|<math>\begin{align}&(y-x)^2=x^2+x+2\\\implies&y=x+\sqrt{x^2+x+2}\ \and\ x=\frac{y^2-2}{1+2y}\\\implies&\mathrm dx=\dots=\frac{2(y^2+y+2)}{(1+2y)^2}\mathrm dy\end{align}</math>}}ואז <math>\int=\frac{\frac{2(y^2+y+2)}{(1+2y)^2}\mathrm dy}{\frac{y^2-2}{1+2y}\frac{y^2+y+2}{1+2y}}=2\int\frac{\mathrm dy}{y^2-2}</math>. {{משל}} | ||
גרסה מ־18:14, 15 במאי 2011
תוכן עניינים
אינטגרציה (המשך)
עד כה דיברנו על אינטגרלים של פונקציות רציונליות (בפרט פולינומים), פונקציות טריגונומטריות וכו'.
עתה נדבר על פונקציות לא רציונליות.
דוגמה 1
חשבו
![\int\frac{\mathrm dx}{x\left(\sqrt x+\sqrt[5]{x^2}\right)}](/images/math/2/1/b/21bab81c3d7cdfcb273267192541db00.png)
פתרון
נרשום את האינטגרל כ-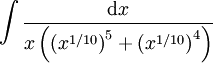 . מתבקשת ההצבה
. מתבקשת ההצבה 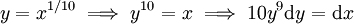 ולכן נקבל
ולכן נקבל 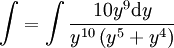 ומכאן קל למצוא את הפתרון.
ומכאן קל למצוא את הפתרון. 
![\int\frac{x^2+\sqrt{1+x}}\sqrt[3]{1+x}\mathrm dx](/images/math/e/e/8/ee89f5e5b475d63d79100f0445446117.png)
פתרון
נגדיר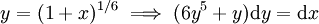 . נקבל
. נקבל  .
. 
הצבות טריגונומטריות
כאשר יש פונקציה מהצורה 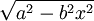 .
.
דוגמה 2
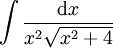
פתרון
נעזר במשלש ישר זווית: גרף (1)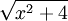 חייב להיות אורך היתר. ההצבה המתבקשת היא
חייב להיות אורך היתר. ההצבה המתבקשת היא 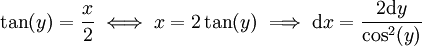 . נקבל נציב
. נקבל נציב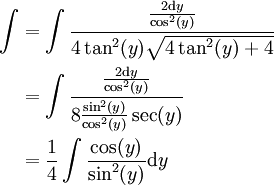
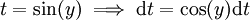 אזי
אזי 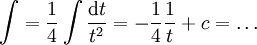 .
. 
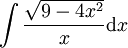
פתרון
שוב נבנה משולש גרף 2. מתבקשת ההצבה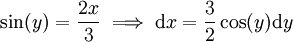 אזי נותר לפתור
אזי נותר לפתור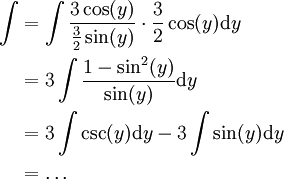
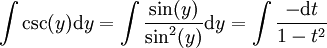 עבור
עבור 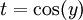 . מכאן נותר רק לפתור בשברים חלקיים.
. מכאן נותר רק לפתור בשברים חלקיים. 
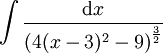
פתרון
ראשית נציב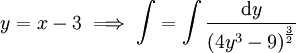 . נציב
. נציב 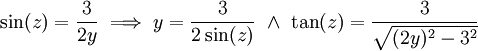 נקבל:
נקבל: 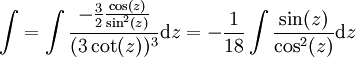 את האינטגרל הנ"ל קל לפתור ע"י הצבה
את האינטגרל הנ"ל קל לפתור ע"י הצבה 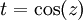 ואז
ואז 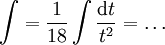 .
. 
הצבות מיוחדות
ההצבה האוניברסלית: תמיד ניתן להציב 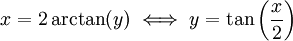 ולכן
ולכן 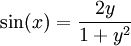 וגם
וגם 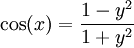 .
.
דוגמה 3
פתור את האינטגרלים הבאים באמצעות ההצבה האוניברסלית:
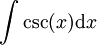
פתרון
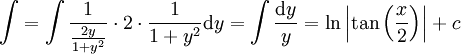

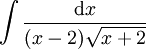
פתרון
נציב
מסקנה: כאשר יש ביטוי מהצורה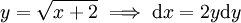 לפיכך
לפיכך 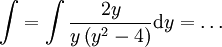 .
. 
![\sqrt[n]{ax+b}](/images/math/8/1/6/81609a67530c44caab097cbce3373a1d.png) ננסה להציב
ננסה להציב 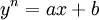 .
.
אם יש ביטוי מהצורה 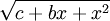 כאשר הפולינום אי פריק נציב
כאשר הפולינום אי פריק נציב 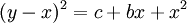 . אם הפולינום בשורש כן פריק ושורשיו
. אם הפולינום בשורש כן פריק ושורשיו 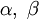 נציב
נציב 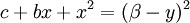 או
או 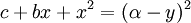 .
.
דוגמה 4
נחשב 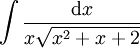
פתרון
הפולינום שבשורש אי פריק, לכן נגדיר y עבורו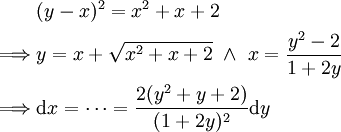
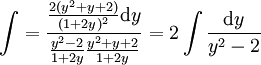 .
. 