הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/10.4.11"
מ (←אינטגרל לא אמיתי {{הערה|(המשך)}}) |
(←משפט 7) |
||
| שורה 68: | שורה 68: | ||
מצד שני, אם f מקיימת את תנאי קושי, אז קיים <math>b>a</math> כך שלכל <math>x_2\ge x_1>b</math> מתקיים <math>|f(x_2)-f(x_1)|<1</math>. נקבע <math>x_1=b+1</math> ונובע שלכל <math>x_2>b+1</math> מתקיים <math>|f(x_2)-f(b+1)|<1</math>. לכן אם <math>x_2>b+1</math> אז <math>|f(x_2)|-|f(b+1)|\le\Big||f(x_2)|-|f(b+1)|\Big|\le|f(x_2)-f(b+1)|<1</math> ומכאן ש-<math>|f(x_2)|<|f(b+1)|+1</math>. לכן f חסומה בקטע <math>[b+1,\infty)</math> ולכן <math>\{f(b+1),\ f(b+2),\ f(b+3),\ \dots\}</math> סדרה חסומה. יש לה תת סדרה מתכנסת <math>\{f(b+n_k)\}_{k\in\mathbb N}</math> כך ש-<math>\lim_{k\to\infty} f(b+n_k)</math> קיים ונאמר שהוא <math>L\in\mathbb R</math>. טענה: <math>\lim_{x\to\infty} f(x)</math> קיים ושווה ל-L. הוכחה: <math>\lim_{k\to\infty} f(b+n_k)=L</math> ולכן עבור <math>\varepsilon>0</math> נתון קיים <math>k_0\in\mathbb N</math> כך שאם <math>k\ge k_0</math> אז <math>|f(b+n_k)-L|<\frac\varepsilon2</math>. כמו כן, עפ"י תנאי קושי יש מספר <math>c>a</math> כך שאם <math>x_2>x_1>c</math> אז <math>|f(x_2)-f(x_1)|<\frac\varepsilon2</math>. עתה נגדיר <math>d:=\max\{b+n_{k_0},c\}</math> ולכן <math>|f(x)-L|\le|f(x)-f(d)|+|f(d)-L|<\frac\varepsilon2+\frac\varepsilon2=\varepsilon</math>. {{משל}} | מצד שני, אם f מקיימת את תנאי קושי, אז קיים <math>b>a</math> כך שלכל <math>x_2\ge x_1>b</math> מתקיים <math>|f(x_2)-f(x_1)|<1</math>. נקבע <math>x_1=b+1</math> ונובע שלכל <math>x_2>b+1</math> מתקיים <math>|f(x_2)-f(b+1)|<1</math>. לכן אם <math>x_2>b+1</math> אז <math>|f(x_2)|-|f(b+1)|\le\Big||f(x_2)|-|f(b+1)|\Big|\le|f(x_2)-f(b+1)|<1</math> ומכאן ש-<math>|f(x_2)|<|f(b+1)|+1</math>. לכן f חסומה בקטע <math>[b+1,\infty)</math> ולכן <math>\{f(b+1),\ f(b+2),\ f(b+3),\ \dots\}</math> סדרה חסומה. יש לה תת סדרה מתכנסת <math>\{f(b+n_k)\}_{k\in\mathbb N}</math> כך ש-<math>\lim_{k\to\infty} f(b+n_k)</math> קיים ונאמר שהוא <math>L\in\mathbb R</math>. טענה: <math>\lim_{x\to\infty} f(x)</math> קיים ושווה ל-L. הוכחה: <math>\lim_{k\to\infty} f(b+n_k)=L</math> ולכן עבור <math>\varepsilon>0</math> נתון קיים <math>k_0\in\mathbb N</math> כך שאם <math>k\ge k_0</math> אז <math>|f(b+n_k)-L|<\frac\varepsilon2</math>. כמו כן, עפ"י תנאי קושי יש מספר <math>c>a</math> כך שאם <math>x_2>x_1>c</math> אז <math>|f(x_2)-f(x_1)|<\frac\varepsilon2</math>. עתה נגדיר <math>d:=\max\{b+n_{k_0},c\}</math> ולכן <math>|f(x)-L|\le|f(x)-f(d)|+|f(d)-L|<\frac\varepsilon2+\frac\varepsilon2=\varepsilon</math>. {{משל}} | ||
| + | |||
| + | |||
| + | <span id="continue"><!--נא לא למחוק span זה--></span>{{הערה|את ההמשך עשינו ב[[משתמש:אור שחף/133 - הרצאה/12.4.11|הרצאה שאחריה]]:}} | ||
| + | |||
| + | ===מסקנה=== | ||
| + | תהי f מוגדרת ואינטגרבילית מקומית ב-<math>[a,\infty)</math>. אזי האינטגרל <math>\int\limits_a^\infty f</math> מתכנס אם"ם האינטגרל מקיים את תנאי קושי: לכל <math>\varepsilon>0</math> קיים <math>x_0>a</math> כך שאם <math>x_2>x_1>x_0</math> אז <math>\left|\int\limits_{x_1}^{x_2} f\right|<\varepsilon</math>. | ||
| + | ====הוכחה==== | ||
| + | לכל <math>x>a</math> נגדיר <math>F(x)=\int\limits_a^x f</math> ולכן <math>\int\limits_{x_1}^{x_2} f=F(x_2)-F(x_1)</math>. כמו כן מתקיים <math>\lim_{x\to\infty}F(x)=\int\limits_a^\infty f</math>. עתה, <math>\lim_{x\to\infty}F(x)</math> מתכנס אם"ם <math>\forall\varepsilon>0:\ \exists x_0>a:\ \forall x_2>x_1>x_0:\ |F(x_2)-F(x_1)|<\varepsilon</math>, וזה נכון אם"ם <math>\forall\varepsilon>0:\ \exists x_0>a:\ \forall x_2>x_1>x_0:\ \left|\int\limits_{x_1}^{x_2} f\right|<\varepsilon</math>. {{משל}} | ||
גרסה מ־17:03, 4 במאי 2011
תוכן עניינים
אינטגרל לא אמיתי, סוג I (המשך)
משפט 4 (מבחן ההשוואה)
נניח ש-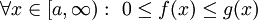 ונניח ש-f,g אינטגרביליות מקומית ב-
ונניח ש-f,g אינטגרביליות מקומית ב- . אזי:
. אזי:
- אם
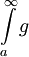 מתכנס אז
מתכנס אז 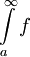 מתכנס.
מתכנס. - אם
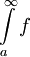 מתבדר אז
מתבדר אז 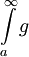 מתבדר.
מתבדר.
הוכחה
- עפ"י משפט 3 מתקיים
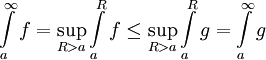 , כלומר
, כלומר 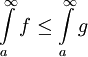 . כעת, אם
. כעת, אם 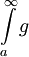 מתכנס אז הוא קטן מ-
מתכנס אז הוא קטן מ-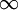 , ולכן
, ולכן 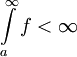 ומתכנס.
ומתכנס. 
- הוכחה טריוויאלית בדרך השלילה, בעזרת סעיף 1.

משפט 5 (מבחן ההשוואה הגבולי)
נניח ש-f ו-g אינטגרביליות מקומית ואי-שליליות ב- . עוד נניח שקיים
. עוד נניח שקיים 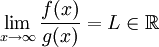 . אם
. אם 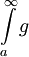 מתכנס אז
מתכנס אז 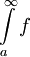 .
.
הוכחה
כיוון ש-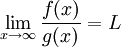 קיים
קיים 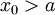 כך שלכל
כך שלכל 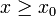 מתקיים
מתקיים 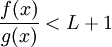 , ז"א
, ז"א 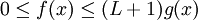 . נתון ש-g אינטגרבילית ב-
. נתון ש-g אינטגרבילית ב- , ולכן, לפי משפט 2, היא אינטגרבילית ב-
, ולכן, לפי משפט 2, היא אינטגרבילית ב-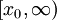 . לפי משפט 1 גם
. לפי משפט 1 גם 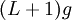 אינטגרבילית ב-
אינטגרבילית ב-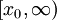 . נובע מכך, יחד עם משפט 4, ש-f אינטגרבילית בקטע
. נובע מכך, יחד עם משפט 4, ש-f אינטגרבילית בקטע 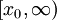 ולפי משפט 2 היא אינטגרבילית ב-
ולפי משפט 2 היא אינטגרבילית ב- .
. 
מסקנה
בתנאים הנ"ל, אם מתקיים גם ש-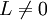 אז
אז 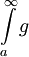 מתכנס אם"ם
מתכנס אם"ם 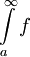 .
.
הוכחה
לפי משפט 5 אם 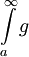 מתכנס אז
מתכנס אז 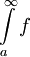 . נותר להוכיח את הכיוון השני. מכיוון ש-
. נותר להוכיח את הכיוון השני. מכיוון ש-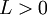 מתקיים
מתקיים 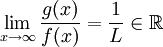 ולכן, שוב לפי משפט 5, אפשר להסיק ש-
ולכן, שוב לפי משפט 5, אפשר להסיק ש-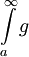 מתכנס אם
מתכנס אם 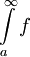 מתכנס.
מתכנס. 
דוגמאות
עבור כל אחד מהאינטגרלים הבאים נבדוק אם הוא מתכנס או מתבדר.
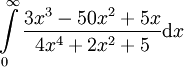 :
:
פתרון
כידוע, עבור x גדול החזקות הגדולות קובעות את סדר הגודל של הביטוי. לכן עבור
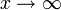 הפונקציה בסדר גודל
הפונקציה בסדר גודל 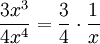 . נגדיר
. נגדיר 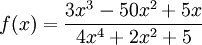 וכן
וכן 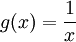 . אזי
. אזי 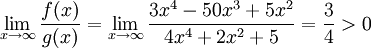 . לכן האינטגרל מתבדר.
. לכן האינטגרל מתבדר. 
-
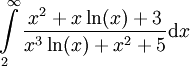 :
:
פתרון
נגדיר
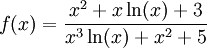 וכן
וכן 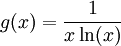 . מתקיים
. מתקיים 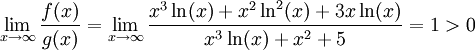 . אבל
. אבל ![\int\limits_2^\infty g=[\ln(\ln(x))]_{x=2}^\infty=\infty](/images/math/2/e/4/2e44fcf11ec977beb440d50203867f19.png) , כלומר מתבדר. לכן גם האינטגרל הנתון מתבדר.
, כלומר מתבדר. לכן גם האינטגרל הנתון מתבדר. 
-
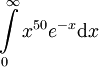 :
:
פתרון
נחשב את
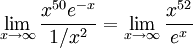 : נפעיל את כלל לופיטל 52 פעמים ונקבל
: נפעיל את כלל לופיטל 52 פעמים ונקבל 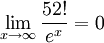 . לכן אם
. לכן אם  מתכנס (מה שאכן מתקיים) אז האינטגרל הנתון מתכנס.
מתכנס (מה שאכן מתקיים) אז האינטגרל הנתון מתכנס. 
משפט 6 (המבחן האינטגרלי לטורים)
נניח ש-f פונקציה יורדת, אי-שלילית ואינטגרבילית מקומית ב-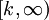 (עבור
(עבור 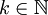 כלשהו). אזי
כלשהו). אזי 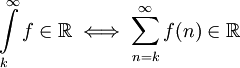 .
.
הוכחה
נזכר בהגדרת דרבו של האינטגרל. 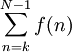 הוא סכום עליון של
הוא סכום עליון של 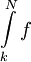 ו-
ו-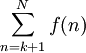 הוא סכום תחתון. נסיק ש-
הוא סכום תחתון. נסיק ש-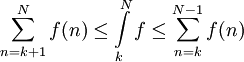 . כעת אם נתון ש-
. כעת אם נתון ש-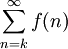 מתכנס אז הסכומים החלקיים
מתכנס אז הסכומים החלקיים 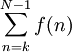 חסומים מלעיל, ומכאן נובע שהאינטגרלים החלקיים
חסומים מלעיל, ומכאן נובע שהאינטגרלים החלקיים 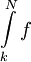 חסומים מלעיל. נשאיף
חסומים מלעיל. נשאיף 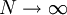 ומכיוון ש-
ומכיוון ש-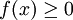 האינטגרל
האינטגרל 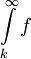 מתכנס. מאידך, אם נתון כי
מתכנס. מאידך, אם נתון כי 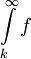 אז האינטגרלים החלקיים
אז האינטגרלים החלקיים 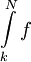 חסומים מלעיל, לכן הסכומים החלקיים
חסומים מלעיל, לכן הסכומים החלקיים 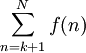 חסומים מלעיל ומכיוון ש-
חסומים מלעיל ומכיוון ש-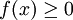 נובע ש-
נובע ש-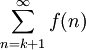 מתכנס
מתכנס 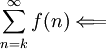 מתכנס.
מתכנס. 
מסקנה
בהוכחה הראינו שבתנאים הללו מתקיים 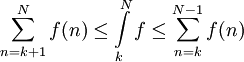 .
.
דוגמאות
-
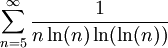 - מתכנס או מתבדר?
- מתכנס או מתבדר?
פתרון
נגדיר
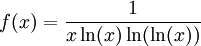 , אזי f יורדת, אינטגרבילית מקומית ואי-שלילית ב-
, אזי f יורדת, אינטגרבילית מקומית ואי-שלילית ב-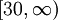 . עפ"י משפט 6 התכנסות הטור שקולה להתכנסות האינטגרל
. עפ"י משפט 6 התכנסות הטור שקולה להתכנסות האינטגרל 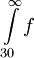 , שמתבדר:
, שמתבדר: ![\int=[\ln(\ln(\ln(x)))]_{x=30}^\infty=\infty](/images/math/5/5/9/5592075921b610fb8f0eed11ae5df0fc.png) (אם כי ההתכנסות איטית מאוד).
(אם כי ההתכנסות איטית מאוד). 
- ידוע לנו ש-
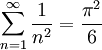 . אם נקח, למשל,
. אם נקח, למשל, 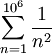 , מהו סדר הגודל של השארית R?
, מהו סדר הגודל של השארית R?
פתרון
נחסום את השארית מלעיל ומלרע בעזרת המסקנה למשפט 6. נגדיר
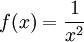 אזי
אזי 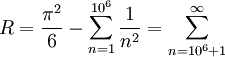 . מתקיים
. מתקיים ![\sum_{n=10^6+1}^\infty\le\int\limits_{10^6}^\infty f=\left[\frac{-1}x\right]_{x=10^6}^\infty=10^{-6}](/images/math/0/2/a/02a03fec7d2f9e9eebb3907eebae4b44.png) . כמו כן
. כמו כן 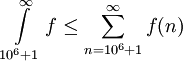 ולכן
ולכן ![\sum_{n=10^6+1}^\infty f(n)\ge\left[\frac{-1}x\right]_{x=10^6+1}^\infty=\frac1{10^6+1}](/images/math/4/b/0/4b0b041571ac24741f997d209da79d4a.png) .
.
לסיכום, השארית מקיימת
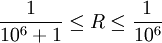 .
.
פיתחנו כמה משפטים על התכנסות 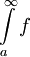 עבור f אי-שלילית. עתה נחזור לפונקציה כללית f שאינטגרבילית מקומית ב-
עבור f אי-שלילית. עתה נחזור לפונקציה כללית f שאינטגרבילית מקומית ב- .
.
הגדרה: תהי f מוגדרת בקטע  . נאמר ש-f מקיימת את תנאי קושי עבור
. נאמר ש-f מקיימת את תנאי קושי עבור 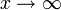 אם לכל
אם לכל  קיים
קיים 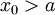 כך שאם
כך שאם 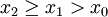 אז
אז 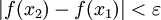 .
.
משפט 7
תהי f מוגדרת בקטע  .
. 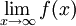 קיים ממש אם"ם הוא מקיים את תנאי קושי בקטע.
קיים ממש אם"ם הוא מקיים את תנאי קושי בקטע.
הוכחה
תחילה נניח שקיים 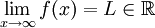 ונאמת את תנאי קושי. יהי
ונאמת את תנאי קושי. יהי  נתון. לפי ההגדרה קיים
נתון. לפי ההגדרה קיים 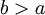 כך שאם
כך שאם 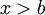 אז
אז 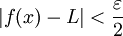 . מכאן נובע שאם
. מכאן נובע שאם 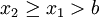 אז
אז 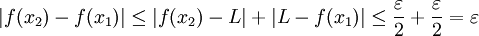 ולכן מתקיים תנאי קושי.
ולכן מתקיים תנאי קושי.
מצד שני, אם f מקיימת את תנאי קושי, אז קיים 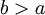 כך שלכל
כך שלכל 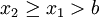 מתקיים
מתקיים 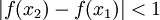 . נקבע
. נקבע 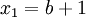 ונובע שלכל
ונובע שלכל 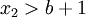 מתקיים
מתקיים 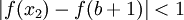 . לכן אם
. לכן אם 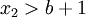 אז
אז 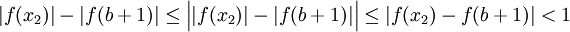 ומכאן ש-
ומכאן ש-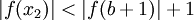 . לכן f חסומה בקטע
. לכן f חסומה בקטע 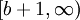 ולכן
ולכן 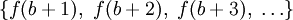 סדרה חסומה. יש לה תת סדרה מתכנסת
סדרה חסומה. יש לה תת סדרה מתכנסת 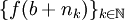 כך ש-
כך ש-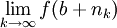 קיים ונאמר שהוא
קיים ונאמר שהוא 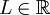 . טענה:
. טענה: 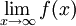 קיים ושווה ל-L. הוכחה:
קיים ושווה ל-L. הוכחה: 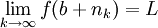 ולכן עבור
ולכן עבור  נתון קיים
נתון קיים 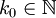 כך שאם
כך שאם 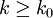 אז
אז 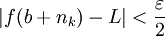 . כמו כן, עפ"י תנאי קושי יש מספר
. כמו כן, עפ"י תנאי קושי יש מספר 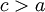 כך שאם
כך שאם 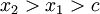 אז
אז 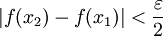 . עתה נגדיר
. עתה נגדיר 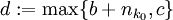 ולכן
ולכן 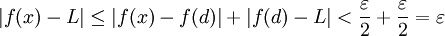 .
. 
את ההמשך עשינו בהרצאה שאחריה:
מסקנה
תהי f מוגדרת ואינטגרבילית מקומית ב- . אזי האינטגרל
. אזי האינטגרל 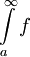 מתכנס אם"ם האינטגרל מקיים את תנאי קושי: לכל
מתכנס אם"ם האינטגרל מקיים את תנאי קושי: לכל  קיים
קיים 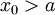 כך שאם
כך שאם 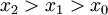 אז
אז 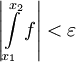 .
.
הוכחה
לכל 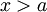 נגדיר
נגדיר 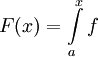 ולכן
ולכן 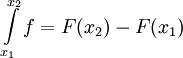 . כמו כן מתקיים
. כמו כן מתקיים 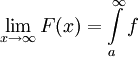 . עתה,
. עתה, 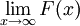 מתכנס אם"ם
מתכנס אם"ם 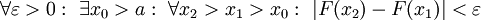 , וזה נכון אם"ם
, וזה נכון אם"ם 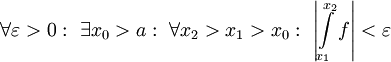 .
. 