הבדלים בין גרסאות בדף "88-101 חשיבה מתמטית קיץ תשעא/תרגילים"
מתוך Math-Wiki
(יצירת דף עם התוכן "=תרגיל להגשה ליום רביעי ה20 ביולי=") |
(←תרגיל להגשה ליום רביעי ה20 ביולי) |
||
| שורה 1: | שורה 1: | ||
| − | =תרגיל להגשה ליום רביעי ה20 ביולי= | + | =תרגיל 1 להגשה ליום רביעי ה20 ביולי= |
| + | ==הצרנות== | ||
| + | *הצרן את הטענות הבאות (מותר לכם להשתמש בפרדיקטים סבירים, בתנאי שתגדירו אותם): | ||
| + | **לכל מספר ממשי יש מספר טבעי הגדול ממנו. | ||
| + | **אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (<math>P(1)\equiv T</math>) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד. | ||
| + | **x הינו מספר ראשוני (מספר המתחלק רק בעצמו ובאחד). | ||
| + | **כל מספר ראשוני הינו סכום של מספרים זוגיים. | ||
| + | **קיימים אינסוף תאומים (תאומים הם זוג ראשוניים אשר ההפרש בינהם הינו שתים.) | ||
| + | |||
| + | ==קבוצות== | ||
| + | הגדרה: איחוד של שתי קבוצות A וB הוא קבוצת האיברים שנמצאים לפחות באחת הקבוצות. החיתוך הוא קבוצת האיברים שנמצאים בשתי הקבוצות. | ||
| + | *הצרן תנאי השקול לכך ש-a שייך לאיחוד של הקבוצות A וB | ||
| + | *הצרן תנאי השקול לכך ש-a אינו שייך לאיחוד של הקבוצות A וB | ||
| + | *הצרן תנאי השקול לכך ש-a שייך לחיתוך של הקבוצות A וB | ||
| + | *הצרן תנאי השקול לכך ש-a אינו שייך לחיתוך של הקבוצות A וB | ||
| + | |||
| + | הגדרה: קבוצה A מוכלת בקבוצה B אם בB נמצאים כל האיברים מA (למשל הטבעיים מוכלים בשלמים <math>\mathbb{N}\subseteq\mathbb{Z}</math>, והשלמים מוכלים בממשיים <math>\mathbb{Z}\subseteq\mathbb{R}</math>). | ||
| + | *הצרן תנאי השקול לכך ש-C מוכלת בחיתוך של A וB | ||
| + | *הצרן תנאי השקול לכך ש-C אינה מוכלת באיחוד של A וB | ||
| + | |||
| + | |||
| + | (מותר לכם להשתמש בכמתים באופן הבא <math>\forall a\in A, \exists a\in A</math>) | ||
גרסה מ־13:17, 18 ביולי 2011
תרגיל 1 להגשה ליום רביעי ה20 ביולי
הצרנות
- הצרן את הטענות הבאות (מותר לכם להשתמש בפרדיקטים סבירים, בתנאי שתגדירו אותם):
- לכל מספר ממשי יש מספר טבעי הגדול ממנו.
- אקסיומת האינדקוציה: אם פרידקט כלשהו אמיתי באחד (
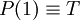 ) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד.
) וכמו כן, העובדה שהוא אמיתי עבור n גוררת שהוא אמיתי עבור n+1 אזי הוא אמיתי תמיד. - x הינו מספר ראשוני (מספר המתחלק רק בעצמו ובאחד).
- כל מספר ראשוני הינו סכום של מספרים זוגיים.
- קיימים אינסוף תאומים (תאומים הם זוג ראשוניים אשר ההפרש בינהם הינו שתים.)
קבוצות
הגדרה: איחוד של שתי קבוצות A וB הוא קבוצת האיברים שנמצאים לפחות באחת הקבוצות. החיתוך הוא קבוצת האיברים שנמצאים בשתי הקבוצות.
- הצרן תנאי השקול לכך ש-a שייך לאיחוד של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a אינו שייך לאיחוד של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a שייך לחיתוך של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a אינו שייך לחיתוך של הקבוצות A וB
הגדרה: קבוצה A מוכלת בקבוצה B אם בB נמצאים כל האיברים מA (למשל הטבעיים מוכלים בשלמים 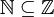 , והשלמים מוכלים בממשיים
, והשלמים מוכלים בממשיים 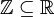 ).
).
- הצרן תנאי השקול לכך ש-C מוכלת בחיתוך של A וB
- הצרן תנאי השקול לכך ש-C אינה מוכלת באיחוד של A וB
(מותר לכם להשתמש בכמתים באופן הבא 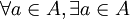 )
)