הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - רשימת משפטים"
מתוך Math-Wiki
| שורה 2: | שורה 2: | ||
* <math>c</math> הוא קבוע. | * <math>c</math> הוא קבוע. | ||
* <math>f,g</math> פונקציות. | * <math>f,g</math> פונקציות. | ||
| − | * | + | * הקטע הנתון הוא הקטע הסגור <math>[a,b]</math>. |
| − | + | * אם מצויין שלפונקציה יש תכונה מסויימת אזי הכוונה לכך שהתכונה מתקיימת בקטע הנתון (למשל: "<math>f</math> חסומה" = "<math>f</math> חסומה ב-<math>[a,b]</math>"). | |
| − | + | ||
| − | : | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
* <math>P</math> היא חלוקה <math>\{x_0,x_1,\dots,x_n\}</math> של הקטע הנתון כך ש-<math>a=x_0<x_1<\dots<x_n=b</math>. | * <math>P</math> היא חלוקה <math>\{x_0,x_1,\dots,x_n\}</math> של הקטע הנתון כך ש-<math>a=x_0<x_1<\dots<x_n=b</math>. | ||
:* <math>Q</math> היא העדנה של <math>P</math>. | :* <math>Q</math> היא העדנה של <math>P</math>. | ||
| − | :* <math>P'=\{a,c_1,c_2,\dots,c_n,b\}</math> היא חלוקה נוספת של הקטע הנוצרת מהחלוקה <math>P</math> כך ש-<math>\forall1\le k\le n:\ c_k\in[x_{k-1},x_k]</math>. | + | :* <math>P'=\{a,c_1,c_2,\dots,c_n,b\}</math> היא חלוקה נוספת של הקטע הנוצרת מהחלוקה <math>P</math> כך ש-<math>\forall1\le k\le n:\ c_k\in[x_{k-1},x_k]</math> ו-<math>\forall 2\le k\le n:\ c_{k-1}\ne c_k</math>. |
=אינטגרלים= | =אינטגרלים= | ||
* אם <math>F</math> ו-<math>G</math> קדומות ל-<math>f</math> בנקודה כלשהי אז קיים <math>c</math> כך ש-<math>F(x)=G(x)+c</math>. | * אם <math>F</math> ו-<math>G</math> קדומות ל-<math>f</math> בנקודה כלשהי אז קיים <math>c</math> כך ש-<math>F(x)=G(x)+c</math>. | ||
| − | * <math> | + | * אם <math>f</math> חסומה ב-<math>[a,b]</math> אזי <math>m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a)</math>. |
| − | * אם <math>|Q|=|P|+r</math> {{הערה|(כלומר, <math>Q</math> מתקבלת מ-<math>P</math> ע"י הוספת <math>r</math> נקודות)}} ו-<math>f | + | * אם <math>|Q|=|P|+r</math> {{הערה|(כלומר, <math>Q</math> מתקבלת מ-<math>P</math> ע"י הוספת <math>r</math> נקודות)}} ו-<math>f</math> חסומה בקטע אזי <math>0\le\overline S(f,P)-\overline S(f,Q)\le r\lambda(P)\Omega</math> וכן <math>0\le\underline S(f,Q)-\underline S(f,P)\le r\lambda(P)\Omega</math>. |
| − | * לכל חלוקה <math>Q</math> של הקטע הנתון (לאו דווקא העדנה של <math>P</math>), אם <math>f | + | * לכל חלוקה <math>Q</math> של הקטע הנתון (לאו דווקא העדנה של <math>P</math>), אם <math>f</math> חסומה בקטע אזי <math>\underline S(f,P)\le\overline S(f,Q)</math>. |
| − | * לכל <math>f | + | * לכל <math>f</math> אינטגרבילית מתקיים <math>\underline\int_a^b f\le\overline{\int}_a^b f</math>. |
| − | * תהי <math>f | + | * תהי <math>f</math> חסומה. אזי <math>\underline\int_a^b f=\lim_{\lambda(P)\to0}\underline S(f,P)</math> וגם <math>\overline{\int}_a^b f=\lim_{\lambda(P)\to0}\overline S(f,P)</math>. |
| − | * נניח ש-<math>f | + | * נניח ש-<math>f</math> חסומה. <math>f</math> אינטגרבילית אם"ם <math>\lim_{\lambda(P)\to0}\overline S(f,P)-\underline S(f,P)=0</math>. |
| − | * נניח ש-<math>f | + | * נניח ש-<math>f</math> חסומה. <math>f</math> אינטגרבילית אם"ם לכל <math>\varepsilon>0</math> קיימת חלוקה <math>P</math> של <math>[a,b]</math> כך ש-<math>\overline S(f,P)-\underline S(f,P)<\varepsilon</math>. |
| − | * אם <math>f | + | * אם <math>f</math> רציפה אז <math>f</math> אינטגרבילית. |
| − | :* {{הערה|הכללה:}} אם <math>f | + | :* {{הערה|הכללה:}} אם <math>f</math> רציפה וחסומה בקטע הפתוח <math>(a,b)</math> אזי <math>f</math> אינטגרבילית. |
| − | ::* {{הערה|הכללה להכללה:}} אם <math>f | + | ::* {{הערה|הכללה להכללה:}} אם <math>f</math> רציפה בקטע בכל נקודה למעט במספר סופי של נקודות והיא חסומה אזי <math>f</math> אינטגרבילית. |
| − | * אם <math>f | + | * אם <math>f</math> מונוטונית אזי היא אינטגרבילית. |
| − | * נניח ש-<math>a<c<b</math>. אזי <math>f | + | * נניח ש-<math>a<c<b</math>. אזי <math>f</math> אינטגרבילית ב-<math>[a,b]</math>, ב-<math>[a,c]</math> וב-<math>[c,b]</math> אם"ם היא אינטגרבילית ב-<math>[a,b]</math>, ואם כן אז <math>\int\limits_a^b f=\int\limits_a^c f+\int\limits_c^b f</math>. |
:* {{הערה|הכללה:}} עבור <math>f</math> כנ"ל ו-<math>a=x_0,x_1,\dots,x_n=b</math> (הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים <math>\int\limits_a^b f=\sum_{k=1}^n\int\limits_{x_{k-1}}^{x_k} f</math>. | :* {{הערה|הכללה:}} עבור <math>f</math> כנ"ל ו-<math>a=x_0,x_1,\dots,x_n=b</math> (הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים <math>\int\limits_a^b f=\sum_{k=1}^n\int\limits_{x_{k-1}}^{x_k} f</math>. | ||
| − | * אם <math>f | + | * אם <math>f</math> חסומה אז <math>\underline S(f,P)\le S(f,P,P')\le\overline S(f,P)</math>. יתר על כן, <math>\underline S(f,P)=\inf_{P'}S(f,P,P')</math> ו-<math>\overline S(f,P)=\sup_{P'}S(f,P,P')</math>. |
* הגדרות האינטגרל לפי דרבו ולפי רימן שקולות. | * הגדרות האינטגרל לפי דרבו ולפי רימן שקולות. | ||
| − | * '''לינאריות:''' <math> | + | * '''לינאריות:''' עבור <math>f,g</math> אינטגרביליות מתקיים <math>\int\limits_a^b f+cg=\int\limits_a^b f+c\int\limits_a^b g</math>. |
| − | * '''מונוטוניות:''' אם <math>f,g | + | * '''מונוטוניות:''' אם <math>f,g</math> אינטגרביליות וכן <math>\forall x\in[a,b]:\ f(x)\ge g(x)</math> אזי <math>\int\limits_a^b f\ge\int\limits_a^b g</math>. |
| − | :* '''חיוביות:''' בפרט מתקיים שאם <math>f | + | :* '''חיוביות:''' בפרט מתקיים שאם <math>f</math> אינטגרביליות ואי-שלילית אזי <math>\int\limits_a^b f\ge0</math>. |
| − | * '''הכללה לאי-שיוויון המשולש:''' אם <math>|f| | + | * '''הכללה לאי-שיוויון המשולש:''' אם <math>|f|</math> אינטגרבילית אז <math>f</math> אינטגרבילית ו-<math>\left|\int\limits_a^b f\right|\le\int\limits_a^b |f|</math>. |
| − | * אם <math>f | + | * אם <math>f</math> אינטגרבילית וחסומה אז <math>m(b-a)\le\int\limits_a^b f\le M(b-a)</math>. |
| − | :* {{הערה|מקרה פרטי:}} אם <math>\forall x\in[a,b]:\ |f(x)|\le M</math> ו-<math>f | + | :* {{הערה|מקרה פרטי:}} אם <math>\forall x\in[a,b]:\ |f(x)|\le M</math> ו-<math>f</math> אינטגרבילית אז <math>\left|\int\limits_a^b f\right|\le M(b-a)</math>. |
::* {{הערה|מקרה פרטי:}} אם <math>f(x)=M</math> (פונקציה קבועה) אז <math>\int\limits_a^b f=M(b-a)</math>. | ::* {{הערה|מקרה פרטי:}} אם <math>f(x)=M</math> (פונקציה קבועה) אז <math>\int\limits_a^b f=M(b-a)</math>. | ||
| − | * '''המשפט היסודי של חשבון אינטגרלי:''' תהי <math>f | + | * '''המשפט היסודי של חשבון אינטגרלי:''' תהי <math>f</math> אינטגרבילית ותהי <math>F</math> כך ש-<math>\forall x\in[a,b]:\ F(x):=\int\limits_a^x f</math>. אזי <math>F</math> רציפה וכן לכל נקודה ב-<math>[a,b]</math> שבה <math>f</math> רציפה, <math>F</math> קדומה ל-<math>f</math> (כלומר, <math>F</math> גזירה ב-<math>[a,b]</math> ו-<math>F'=f</math>). |
| − | * '''נוסחת ניוטון-לייבניץ:''' תהי <math>f | + | * '''נוסחת ניוטון-לייבניץ:''' תהי <math>f</math> רציפה. אזי <math>\int\limits_a^b f=[F(x)]_{x=a}^b=F(b)-F(a)</math>. |
| − | * לכל <math>f | + | * לכל <math>f</math> רציפה יש פונקציה קדומה. |
* '''אינטגרציה בחלקים:''' נניח כי <math>f',g'</math> רציפות. אזי <math>\int f(x)g(x)\mathrm dx=f(x)g(x)-\int f'(x)g(x)\mathrm dx</math>. | * '''אינטגרציה בחלקים:''' נניח כי <math>f',g'</math> רציפות. אזי <math>\int f(x)g(x)\mathrm dx=f(x)g(x)-\int f'(x)g(x)\mathrm dx</math>. | ||
:* <math>\int\limits_a^b f\cdot g'=[f(x)g(x)]_{x=a}^b-\int\limits_a^b f'\cdot g</math> | :* <math>\int\limits_a^b f\cdot g'=[f(x)g(x)]_{x=a}^b-\int\limits_a^b f'\cdot g</math> | ||
| שורה 49: | שורה 40: | ||
:* <math>\int\limits_a^b f(g(x))g'(x)\mathrm dx=\int\limits_{g(a)}^{g(b)}f(g(x))\mathrm dg(x)</math> | :* <math>\int\limits_a^b f(g(x))g'(x)\mathrm dx=\int\limits_{g(a)}^{g(b)}f(g(x))\mathrm dg(x)</math> | ||
* כל פונקציה רציונלית <math>\frac pq</math> כך ש-<math>\deg(p)<\deg(q)</math> ניתנת לפירוק יחיד כסכום של שברים חלקיים <math>\frac A{(x-x_0)^n}+\frac{Bx+c}{(x^2+bx+c)^k}</math> כאשר <math>A,B,C,x_0\in\mathbb R</math> ול-<math>x^2+bx+c</math> אין שורשים ממשיים. | * כל פונקציה רציונלית <math>\frac pq</math> כך ש-<math>\deg(p)<\deg(q)</math> ניתנת לפירוק יחיד כסכום של שברים חלקיים <math>\frac A{(x-x_0)^n}+\frac{Bx+c}{(x^2+bx+c)^k}</math> כאשר <math>A,B,C,x_0\in\mathbb R</math> ול-<math>x^2+bx+c</math> אין שורשים ממשיים. | ||
| − | * נפח גוף הסיבוב הנוצר מסיבוב השטח שמתחת ל-<math>f | + | * נפח גוף הסיבוב הנוצר מסיבוב השטח שמתחת ל-<math>f</math> אי-שלילית בין <math>a</math> ל-<math>b</math> סביב ציר ה-<math>x</math> הוא <math>\int\limits_a^b \pi f^2</math>. |
| − | * | + | * אם <math>f</math> רציפה אז הממוצע שלה בקטע <math>[a,b]</math> הוא <math>\frac1{b-a}\int\limits_a^b f</math>. |
| − | * | + | * אם <math>f</math> בעלת גזירה אז אורך הגרף שלה בקטע <math>[a,b]</math> הוא <math>\int\limits_a^b\sqrt{1+f'(x)^2}\mathrm dx</math>. |
| − | * שטח המעטפת (ללא הבסיסים) של גוף סיבוב הנוצר מסיבוב הגרף של <math>f | + | * שטח המעטפת (ללא הבסיסים) של גוף סיבוב הנוצר מסיבוב הגרף של <math>f</math> רציפה סביב ציר ה-<math>x</math> בקטע <math>[a,b]</math> הוא <math>\int\limits_a^b 2\pi f(x)\sqrt{1+f'(x)^2}\mathrm dx</math>. |
| − | + | * תהא <math>f</math> בעלת נגזרת <math>n</math>-ית רציפה. אזי <math>\int\limits_a^b f\approx\int\limits_a^b P_n</math> כאשר <math>P_n</math> הוא פיתוח טיילור מסדר <math>n</math> של <math>f</math> והשארית חסומה ע"י <math>\int\limits_a^b R_n=f^{(n+1)}(c)\frac{b^{n+2}-a^{n+2}}{(n+2)!}</math>. | |
| − | * תהא <math>f | + | * תהא <math>f</math> בעלת נגזרת רציפה והחלוקה <math>P</math> היא חלוקה שווה כאשר לכל <math>k</math> מתקיים <math>\Delta x_k=h</math>. אזי <math>\int\limits_a^b f\approx h\sum_{k=1}^n f(x_k)</math> והשארית חסומה ע"י <math>\frac{b-a}2Mh</math> כאשר <math>M=\max_{x\in[a,b]}\left|f'(x)\right|</math>. |
| − | * | + | * תהא <math>f</math> בעלת נגזרת שנייה רציפה והחלוקה <math>P</math> היא חלוקה שווה כאשר לכל <math>k</math> מתקיים <math>\Delta x_k=h</math>. אזי <math>\int\limits_a^b f\approx h\frac{f(x_0)+f(x_n)}2+h\sum_{k=1}^{n-1}f(x_k)</math> והשארית חסומה ע"י <math>\frac5{12}(b-a)Mh^2</math> כאשר <math>M=\max_{x\in[a,b]}\left|f''(x)\right|</math>. |
| − | + | * תהא <math>f</math> בעלת נגזרת רביעית רציפה והחלוקה <math>P</math> היא חלוקה שווה כאשר לכל <math>k</math> מתקיים <math>\Delta x_k=h</math> ו-<math>n</math> זוגי. אזי <math>\int\limits_a^b f\approx\frac h3\left(f(x_0)+4\sum_{k=1}^{n/2} f(x_{2k-1})+2\sum_{k=1}^{n/2-1}f(x_{2k})+f(x_n)\right)</math> והשגיאה חסומה ע"י <math>\frac{b-a}{180}Mh^4</math> כאשר <math>M=\max_{x\in[a,b]}\left|f^{(4)}(x)\right|</math>. | |
| − | * | + | * תהיינה <math>f,g</math> אינטגרביליות ב-<math>[a,\infty)</math>. אזי <math>f+cg</math> אינטגרבילית ב-<math>[a,\infty)</math> ומתקיים <math>\int\limits_a^\infty f+cg=\int\limits_a^\infty f+c\int\limits_a^\infty g</math>. |
| − | * תהא <math>f | + | * תהא <math>f</math> אינטגרבילית מקומית ב-<math>[a,\infty)</math> ויהי <math>b>a</math>. אזי <math>f</math> אינטגרבילית ב-<math>[a,\infty)</math> אם"ם <math>f</math> אינטגרבילית ב-<math>[b,\infty)</math> ואם כן <math>\int\limits_a^\infty f=\int\limits_a^b f+\int\limits_b^\infty f</math>. |
| − | * <math>f | + | * <math>f</math> מונוטונית עולה ב-<math>[a,\infty)</math>. אזי <math>\lim_{x\to\infty} f(x)</math> קיים אם"ם <math>\sup_x f(x)<\infty</math> ואם כן <math>\lim_{x\to\infty} f(x)=\sup_{x>a} f(x)</math>. |
| − | * <math>f | + | * <math>f</math> אי-שלילית ואינטגרבילית מקומית ב-<math>[a,\infty)</math>. אזי <math>\int\limits_a^\infty f</math> מתכנס אם"ם האינטגרלים החלקיים <math>\int\limits_a^R f</math> חסומים מלעיל, ואם לא אז <math>\int\limits_a^\infty f=\infty</math>. |
| − | * '''מבחן ההשוואה:''' נניח ש-<math>f,g | + | * '''מבחן ההשוואה:''' נניח ש-<math>f,g</math> אי-שליליות ואינטגרביליות מקומית ב-<math>[a,\infty)</math> וכן <math>\forall x\in[a,\infty):\ f(x)\le g(x)</math>. אם <math>\int\limits_a^\infty g</math> מתכנס אז <math>\int\limits_a^\infty f</math> מתכנס. |
| − | * '''מבחן ההשוואה הגבולי:''' <math>f,g | + | * '''מבחן ההשוואה הגבולי:''' <math>f,g</math> אי-שליליות ואינטגרביליות מקומית ב-<math>[a,\infty)</math> וכן <math>\lim_{x\to\infty}\frac{f(x)}{g(x)}\in\mathbb R</math>. אם <math>\int\limits_a^\infty g</math> מתכנס אז <math>\int\limits_a^\infty f</math> מתכנס. |
:* {{הערה|מקרה פרטי:}} אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד. | :* {{הערה|מקרה פרטי:}} אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד. | ||
| − | * '''המבחן האינטגרלי לטורים:''' תהא <math>f | + | * '''המבחן האינטגרלי לטורים:''' תהא <math>f</math> אי-שלילית, מונוטונית יורדת ואינטגרבילית מקומית ב-<math>[k,\infty)</math> עבור <math>k\in\mathbb N</math> כלשהו. אזי <math>\int\limits_k^\infty f</math> מתכנס אם"ם <math>\sum_{n=k}^\infty f(n)</math> מתכנס. |
:* {{הערה|הכללה:}} בפרט מתקיים <math>\sum_{n=k+1}^N f(n)\le\int\limits_k^N f\le\sum_{n=k}^{N-1} f(n)</math>. | :* {{הערה|הכללה:}} בפרט מתקיים <math>\sum_{n=k+1}^N f(n)\le\int\limits_k^N f\le\sum_{n=k}^{N-1} f(n)</math>. | ||
* תהא <math>f</math> מוגדרת ב-<math>[a,\infty)</math>. <math>\lim_{x\to\infty} f(x)</math> קיים אם"ם הוא מקיים את תנאי קושי בקטע. | * תהא <math>f</math> מוגדרת ב-<math>[a,\infty)</math>. <math>\lim_{x\to\infty} f(x)</math> קיים אם"ם הוא מקיים את תנאי קושי בקטע. | ||
| − | * תהא <math>f | + | * תהא <math>f</math> אינטגרבילית מקומית ב-<math>[a,\infty)</math>. אזי <math>\int\limits_a^\infty f</math> מתכנס אם"ם <math>\forall\varepsilon>0:\ \exists x_0>a:\ \forall x_2>x_1>x_0:\ \left|\int\limits_{x_1}^{x_2} f\right|<\varepsilon</math>. |
| − | * תהא <math>f | + | * תהא <math>f</math> אינטגרבילית מקומית ב-<math>[a,\infty)</math>. אם <math>|f|</math> אינטגרבילית בקטע אזי גם <math>f</math> אינטגרבילית בו. |
| − | * '''מבחן דיריכלה:''' תהא <math>f | + | * '''מבחן דיריכלה:''' תהא <math>f</math> רציפה ב-<math>[a,\infty)</math> ונניח שהאינטגרלים החלקיים <math>\int\limits_a^b f</math> חסומים כאשר <math>b\to\infty</math>. כמו כן תהא <math>g</math> מונוטונית ובעלת נגזרת רציפה ב-<math>[a,\infty)</math> ו-<math>\lim_{x\to\infty}g(x)=0</math>. אזי <math>\int\limits_a^\infty f\cdot g</math> מתכנס. |
* '''סכימה בחלקים:''' <math>\sum_{n=1}^N a_nb_n=\sum_{n=1}^{N-1}S_n(b_n-b_{n+1})+S_Nb_N</math> כאשר <math>S_n=\sum_{k=1}^n a_k</math>. | * '''סכימה בחלקים:''' <math>\sum_{n=1}^N a_nb_n=\sum_{n=1}^{N-1}S_n(b_n-b_{n+1})+S_Nb_N</math> כאשר <math>S_n=\sum_{k=1}^n a_k</math>. | ||
* '''משפט דיריכלה לטורים:''' נניח שלטור <math>\sum_{n=1}^N a_n</math> יש סכומים חלקיים חסומים ונניח ש-<math>\{b_n\}</math> סדרה מונוטונית כך ש-<math>b_n\to0</math>. אזי <math>\sum_{n=1}^\infty a_nb_n</math> מתכנס. | * '''משפט דיריכלה לטורים:''' נניח שלטור <math>\sum_{n=1}^N a_n</math> יש סכומים חלקיים חסומים ונניח ש-<math>\{b_n\}</math> סדרה מונוטונית כך ש-<math>b_n\to0</math>. אזי <math>\sum_{n=1}^\infty a_nb_n</math> מתכנס. | ||
| − | * אם <math>f,g | + | * אם <math>f,g</math> אינטגרביליות ב-<math>(a,b]</math> אזי לכל <math>c</math> מתקיים <math>\int\limits_a^b f+cg=\int\limits_a^b f+c\int\limits_a^b g</math>. |
| − | * עבור <math>a<c<b</math> ו-<math>f | + | * עבור <math>a<c<b</math> ו-<math>f</math> אינטגרבילית מקומית ב-<math>(a,b]</math>, <math>f</math> אינטגרבילית בקטע אם"ם <math>f</math> אינטגרבילית ב-<math>(a,c]</math>, ואם כן <math>\int\limits_a^b f=\int\limits_a^c+\int\limits_b^c f</math>. |
| − | * תהי <math>f | + | * תהי <math>f</math> מונוטונית ב-<math>(a,b]</math>. אזי <math>\lim_{x\to a^+}f(x)</math> קיים אם"ם <math>f</math> חסומה ב-<math>(a,b]</math>. |
| − | * אם <math>f | + | * אם <math>f</math> אי-שלילית ואינטגרבילית מקומית ב-<math>(a,b]</math> אז <math>f</math> אינטגרבילית ב-<math>(a,b]</math> אם"ם האינטגרלים החלקיים <math>\int\limits_c^b f</math> חסומים כאשר <math>c\to a^+</math>. |
| − | * '''מבחן ההשוואה:''' <math>f,g | + | * '''מבחן ההשוואה:''' <math>f,g</math> אי-שליליות ואינטגרביליות מקומיות ב-<math>(a,b]</math> וכן <math>\forall \in(a,b]:\ f(x)\le g(x)</math>. אם <math>\int\limits_a^b g</math> מתכנס אזי <math>\int\limits_a^b f</math> מתכנס. |
| − | * '''מבחן ההשוואה הגבולי:''' <math>f,g | + | * '''מבחן ההשוואה הגבולי:''' <math>f,g</math> אי-שליליות ואינטגרביליות מקומית ב-<math>(a,b]</math> וקיים <math>\lim_{x\to a^+}\frac{f(x)}{g(x)}</math>. אם <math>\int\limits_a^b g</math> מתכנס אז <math>\int\limits_a^b f</math> מתכנס. |
:* {{הערה|מקרה פרטי:}} אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד. | :* {{הערה|מקרה פרטי:}} אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד. | ||
| − | * תהא <math>f | + | * תהא <math>f</math> אינטגרבילית מקומית ב-<math>(a,b]</math>. אזי <math>\int\limits_a^b f</math> מתכנס אם"ם <math>\forall\varepsilon>0:\ \exists x_0\in(a,b):\ \forall a<x_1<x_2<x_0:\ \left|\int\limits_{x_1}^{x_2}f\right|<\varepsilon</math>. |
| − | * תהא <math>f | + | * תהא <math>f</math> אינטגרבילית מקומית ב-<math>(a,b]</math>. אם <math>\int\limits_a^b |f|</math> מתכנס אז <math>\int\limits_a^b f</math> מתכנס. |
גרסה מ־17:09, 25 ביולי 2011
במשפטים הבאים, אלא אם צויין אחרת, נסמן:
-
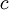 הוא קבוע.
הוא קבוע. -
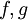 פונקציות.
פונקציות. - הקטע הנתון הוא הקטע הסגור
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. - אם מצויין שלפונקציה יש תכונה מסויימת אזי הכוונה לכך שהתכונה מתקיימת בקטע הנתון (למשל: "
 חסומה" = "
חסומה" = " חסומה ב-
חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ").
"). -
 היא חלוקה
היא חלוקה 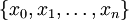 של הקטע הנתון כך ש-
של הקטע הנתון כך ש-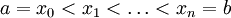 .
.
-
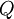 היא העדנה של
היא העדנה של  .
. -
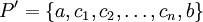 היא חלוקה נוספת של הקטע הנוצרת מהחלוקה
היא חלוקה נוספת של הקטע הנוצרת מהחלוקה  כך ש-
כך ש-![\forall1\le k\le n:\ c_k\in[x_{k-1},x_k]](/images/math/6/9/a/69a81d3601befa0c225b704fa40e9731.png) ו-
ו-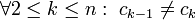 .
.
-
אינטגרלים
- אם
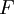 ו-
ו-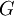 קדומות ל-
קדומות ל- בנקודה כלשהי אז קיים
בנקודה כלשהי אז קיים 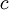 כך ש-
כך ש-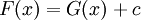 .
. - אם
 חסומה ב-
חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אזי
אזי 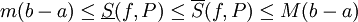 .
. - אם
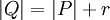 (כלומר,
(כלומר, 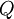 מתקבלת מ-
מתקבלת מ- ע"י הוספת
ע"י הוספת 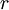 נקודות) ו-
נקודות) ו- חסומה בקטע אזי
חסומה בקטע אזי 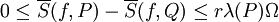 וכן
וכן 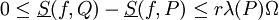 .
. - לכל חלוקה
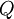 של הקטע הנתון (לאו דווקא העדנה של
של הקטע הנתון (לאו דווקא העדנה של  ), אם
), אם  חסומה בקטע אזי
חסומה בקטע אזי 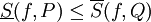 .
. - לכל
 אינטגרבילית מתקיים
אינטגרבילית מתקיים 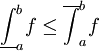 .
. - תהי
 חסומה. אזי
חסומה. אזי 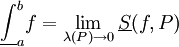 וגם
וגם 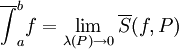 .
. - נניח ש-
 חסומה.
חסומה.  אינטגרבילית אם"ם
אינטגרבילית אם"ם 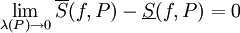 .
. - נניח ש-
 חסומה.
חסומה.  אינטגרבילית אם"ם לכל
אינטגרבילית אם"ם לכל  קיימת חלוקה
קיימת חלוקה  של
של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-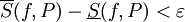 .
. - אם
 רציפה אז
רציפה אז  אינטגרבילית.
אינטגרבילית.
- הכללה: אם
 רציפה וחסומה בקטע הפתוח
רציפה וחסומה בקטע הפתוח 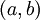 אזי
אזי  אינטגרבילית.
אינטגרבילית.
- הכללה להכללה: אם
 רציפה בקטע בכל נקודה למעט במספר סופי של נקודות והיא חסומה אזי
רציפה בקטע בכל נקודה למעט במספר סופי של נקודות והיא חסומה אזי  אינטגרבילית.
אינטגרבילית.
- הכללה להכללה: אם
- הכללה: אם
- אם
 מונוטונית אזי היא אינטגרבילית.
מונוטונית אזי היא אינטגרבילית. - נניח ש-
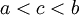 . אזי
. אזי  אינטגרבילית ב-
אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ב-
, ב-![[a,c]](/images/math/2/0/9/209f61583177d88b1f24c85f6a43c6ff.png) וב-
וב-![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) אם"ם היא אינטגרבילית ב-
אם"ם היא אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ואם כן אז
, ואם כן אז 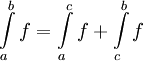 .
.
- הכללה: עבור
 כנ"ל ו-
כנ"ל ו-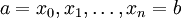 (הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים
(הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים 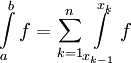 .
.
- הכללה: עבור
- אם
 חסומה אז
חסומה אז 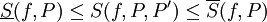 . יתר על כן,
. יתר על כן, 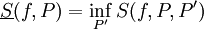 ו-
ו-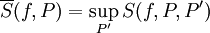 .
. - הגדרות האינטגרל לפי דרבו ולפי רימן שקולות.
- לינאריות: עבור
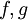 אינטגרביליות מתקיים
אינטגרביליות מתקיים 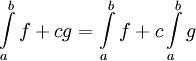 .
. - מונוטוניות: אם
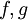 אינטגרביליות וכן
אינטגרביליות וכן ![\forall x\in[a,b]:\ f(x)\ge g(x)](/images/math/b/0/f/b0f5c358a40311d0e8e99133603633c2.png) אזי
אזי 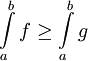 .
.
- חיוביות: בפרט מתקיים שאם
 אינטגרביליות ואי-שלילית אזי
אינטגרביליות ואי-שלילית אזי 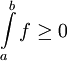 .
.
- חיוביות: בפרט מתקיים שאם
- הכללה לאי-שיוויון המשולש: אם
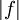 אינטגרבילית אז
אינטגרבילית אז  אינטגרבילית ו-
אינטגרבילית ו-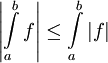 .
. - אם
 אינטגרבילית וחסומה אז
אינטגרבילית וחסומה אז 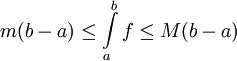 .
.
- מקרה פרטי: אם
![\forall x\in[a,b]:\ |f(x)|\le M](/images/math/1/6/b/16b3029642875feb621b346dca19885e.png) ו-
ו- אינטגרבילית אז
אינטגרבילית אז 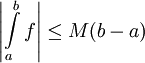 .
.
- מקרה פרטי: אם
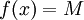 (פונקציה קבועה) אז
(פונקציה קבועה) אז 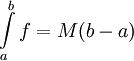 .
.
- מקרה פרטי: אם
- מקרה פרטי: אם
- המשפט היסודי של חשבון אינטגרלי: תהי
 אינטגרבילית ותהי
אינטגרבילית ותהי 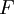 כך ש-
כך ש-![\forall x\in[a,b]:\ F(x):=\int\limits_a^x f](/images/math/0/c/5/0c5f442e2899834dd8dae25116fd3194.png) . אזי
. אזי 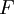 רציפה וכן לכל נקודה ב-
רציפה וכן לכל נקודה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) שבה
שבה  רציפה,
רציפה, 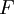 קדומה ל-
קדומה ל- (כלומר,
(כלומר, 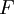 גזירה ב-
גזירה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ו-
ו-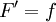 ).
). - נוסחת ניוטון-לייבניץ: תהי
 רציפה. אזי
רציפה. אזי ![\int\limits_a^b f=[F(x)]_{x=a}^b=F(b)-F(a)](/images/math/9/9/1/9910c3fea84d530a4ddc29cee79f0db3.png) .
. - לכל
 רציפה יש פונקציה קדומה.
רציפה יש פונקציה קדומה. - אינטגרציה בחלקים: נניח כי
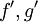 רציפות. אזי
רציפות. אזי 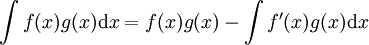 .
.
- שיטת ההצבה:
 .
.
- כל פונקציה רציונלית
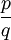 כך ש-
כך ש-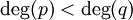 ניתנת לפירוק יחיד כסכום של שברים חלקיים
ניתנת לפירוק יחיד כסכום של שברים חלקיים 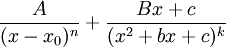 כאשר
כאשר 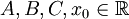 ול-
ול-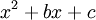 אין שורשים ממשיים.
אין שורשים ממשיים. - נפח גוף הסיבוב הנוצר מסיבוב השטח שמתחת ל-
 אי-שלילית בין
אי-שלילית בין  ל-
ל-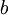 סביב ציר ה-
סביב ציר ה- הוא
הוא  .
. - אם
 רציפה אז הממוצע שלה בקטע
רציפה אז הממוצע שלה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 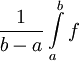 .
. - אם
 בעלת גזירה אז אורך הגרף שלה בקטע
בעלת גזירה אז אורך הגרף שלה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 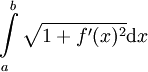 .
. - שטח המעטפת (ללא הבסיסים) של גוף סיבוב הנוצר מסיבוב הגרף של
 רציפה סביב ציר ה-
רציפה סביב ציר ה- בקטע
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 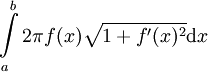 .
. - תהא
 בעלת נגזרת
בעלת נגזרת  -ית רציפה. אזי
-ית רציפה. אזי 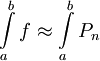 כאשר
כאשר 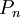 הוא פיתוח טיילור מסדר
הוא פיתוח טיילור מסדר  של
של  והשארית חסומה ע"י
והשארית חסומה ע"י 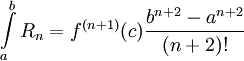 .
. - תהא
 בעלת נגזרת רציפה והחלוקה
בעלת נגזרת רציפה והחלוקה  היא חלוקה שווה כאשר לכל
היא חלוקה שווה כאשר לכל 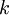 מתקיים
מתקיים 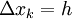 . אזי
. אזי 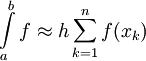 והשארית חסומה ע"י
והשארית חסומה ע"י 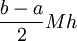 כאשר
כאשר ![M=\max_{x\in[a,b]}\left|f'(x)\right|](/images/math/a/f/5/af58485a1bb5b1e2ba25c07c21c81506.png) .
. - תהא
 בעלת נגזרת שנייה רציפה והחלוקה
בעלת נגזרת שנייה רציפה והחלוקה  היא חלוקה שווה כאשר לכל
היא חלוקה שווה כאשר לכל 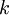 מתקיים
מתקיים 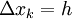 . אזי
. אזי  והשארית חסומה ע"י
והשארית חסומה ע"י 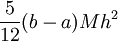 כאשר
כאשר ![M=\max_{x\in[a,b]}\left|f''(x)\right|](/images/math/1/8/2/1821a4640ed7cc006f943ace2590eaa8.png) .
. - תהא
 בעלת נגזרת רביעית רציפה והחלוקה
בעלת נגזרת רביעית רציפה והחלוקה  היא חלוקה שווה כאשר לכל
היא חלוקה שווה כאשר לכל 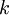 מתקיים
מתקיים 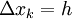 ו-
ו- זוגי. אזי
זוגי. אזי  והשגיאה חסומה ע"י
והשגיאה חסומה ע"י 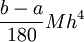 כאשר
כאשר ![M=\max_{x\in[a,b]}\left|f^{(4)}(x)\right|](/images/math/c/0/b/c0b6d228eaf7256cb8ed55af82c13b6e.png) .
. - תהיינה
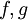 אינטגרביליות ב-
אינטגרביליות ב- . אזי
. אזי 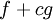 אינטגרבילית ב-
אינטגרבילית ב- ומתקיים
ומתקיים 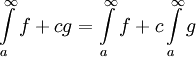 .
. - תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב- ויהי
ויהי 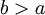 . אזי
. אזי  אינטגרבילית ב-
אינטגרבילית ב- אם"ם
אם"ם  אינטגרבילית ב-
אינטגרבילית ב-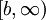 ואם כן
ואם כן 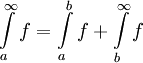 .
. -
 מונוטונית עולה ב-
מונוטונית עולה ב- . אזי
. אזי 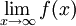 קיים אם"ם
קיים אם"ם 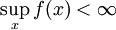 ואם כן
ואם כן 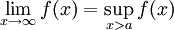 .
. -
 אי-שלילית ואינטגרבילית מקומית ב-
אי-שלילית ואינטגרבילית מקומית ב- . אזי
. אזי 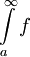 מתכנס אם"ם האינטגרלים החלקיים
מתכנס אם"ם האינטגרלים החלקיים 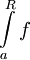 חסומים מלעיל, ואם לא אז
חסומים מלעיל, ואם לא אז 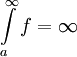 .
. - מבחן ההשוואה: נניח ש-
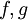 אי-שליליות ואינטגרביליות מקומית ב-
אי-שליליות ואינטגרביליות מקומית ב- וכן
וכן 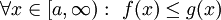 . אם
. אם 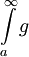 מתכנס אז
מתכנס אז 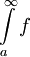 מתכנס.
מתכנס. - מבחן ההשוואה הגבולי:
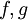 אי-שליליות ואינטגרביליות מקומית ב-
אי-שליליות ואינטגרביליות מקומית ב- וכן
וכן 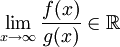 . אם
. אם 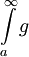 מתכנס אז
מתכנס אז 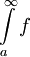 מתכנס.
מתכנס.
- מקרה פרטי: אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד.
- המבחן האינטגרלי לטורים: תהא
 אי-שלילית, מונוטונית יורדת ואינטגרבילית מקומית ב-
אי-שלילית, מונוטונית יורדת ואינטגרבילית מקומית ב-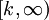 עבור
עבור 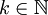 כלשהו. אזי
כלשהו. אזי 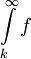 מתכנס אם"ם
מתכנס אם"ם 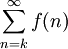 מתכנס.
מתכנס.
- הכללה: בפרט מתקיים
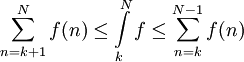 .
.
- הכללה: בפרט מתקיים
- תהא
 מוגדרת ב-
מוגדרת ב- .
. 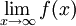 קיים אם"ם הוא מקיים את תנאי קושי בקטע.
קיים אם"ם הוא מקיים את תנאי קושי בקטע. - תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב- . אזי
. אזי 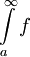 מתכנס אם"ם
מתכנס אם"ם 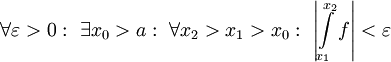 .
. - תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב- . אם
. אם 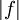 אינטגרבילית בקטע אזי גם
אינטגרבילית בקטע אזי גם  אינטגרבילית בו.
אינטגרבילית בו. - מבחן דיריכלה: תהא
 רציפה ב-
רציפה ב- ונניח שהאינטגרלים החלקיים
ונניח שהאינטגרלים החלקיים 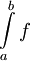 חסומים כאשר
חסומים כאשר 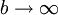 . כמו כן תהא
. כמו כן תהא 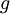 מונוטונית ובעלת נגזרת רציפה ב-
מונוטונית ובעלת נגזרת רציפה ב- ו-
ו-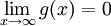 . אזי
. אזי 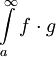 מתכנס.
מתכנס. - סכימה בחלקים:
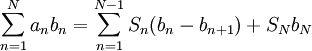 כאשר
כאשר 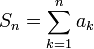 .
. - משפט דיריכלה לטורים: נניח שלטור
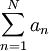 יש סכומים חלקיים חסומים ונניח ש-
יש סכומים חלקיים חסומים ונניח ש-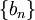 סדרה מונוטונית כך ש-
סדרה מונוטונית כך ש-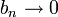 . אזי
. אזי 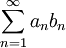 מתכנס.
מתכנס. - אם
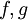 אינטגרביליות ב-
אינטגרביליות ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) אזי לכל
אזי לכל 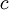 מתקיים
מתקיים 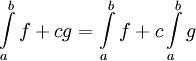 .
. - עבור
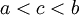 ו-
ו- אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) ,
,  אינטגרבילית בקטע אם"ם
אינטגרבילית בקטע אם"ם  אינטגרבילית ב-
אינטגרבילית ב-![(a,c]](/images/math/0/4/2/0425cdec60417e93bfbb1720291ef9f4.png) , ואם כן
, ואם כן 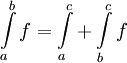 .
. - תהי
 מונוטונית ב-
מונוטונית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אזי
. אזי 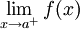 קיים אם"ם
קיים אם"ם  חסומה ב-
חסומה ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) .
. - אם
 אי-שלילית ואינטגרבילית מקומית ב-
אי-שלילית ואינטגרבילית מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) אז
אז  אינטגרבילית ב-
אינטגרבילית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) אם"ם האינטגרלים החלקיים
אם"ם האינטגרלים החלקיים 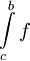 חסומים כאשר
חסומים כאשר 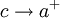 .
. - מבחן ההשוואה:
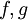 אי-שליליות ואינטגרביליות מקומיות ב-
אי-שליליות ואינטגרביליות מקומיות ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) וכן
וכן ![\forall \in(a,b]:\ f(x)\le g(x)](/images/math/5/8/c/58c4610fb4b7f5aaf8af8d7d532b97a8.png) . אם
. אם 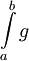 מתכנס אזי
מתכנס אזי 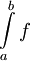 מתכנס.
מתכנס. - מבחן ההשוואה הגבולי:
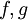 אי-שליליות ואינטגרביליות מקומית ב-
אי-שליליות ואינטגרביליות מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) וקיים
וקיים 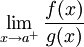 . אם
. אם 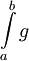 מתכנס אז
מתכנס אז 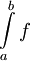 מתכנס.
מתכנס.
- מקרה פרטי: אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד.
- תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אזי
. אזי 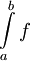 מתכנס אם"ם
מתכנס אם"ם 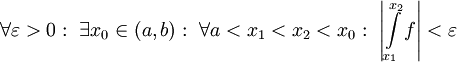 .
. - תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אם
. אם 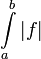 מתכנס אז
מתכנס אז 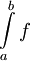 מתכנס.
מתכנס.
![\int\limits_a^b f\cdot g'=[f(x)g(x)]_{x=a}^b-\int\limits_a^b f'\cdot g](/images/math/1/9/b/19b8bd99dab83c15e4420a086d20b431.png)