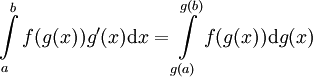הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - רשימת משפטים"
מתוך Math-Wiki
מ |
|||
| שורה 72: | שורה 72: | ||
* תהא <math>f</math> אינטגרבילית מקומית ב-<math>(a,b]</math>. אזי <math>\int\limits_a^b f</math> מתכנס אם"ם <math>\forall\varepsilon>0:\ \exists x_0\in(a,b):\ \forall a<x_1<x_2<x_0:\ \left|\int\limits_{x_1}^{x_2}f\right|<\varepsilon</math>. | * תהא <math>f</math> אינטגרבילית מקומית ב-<math>(a,b]</math>. אזי <math>\int\limits_a^b f</math> מתכנס אם"ם <math>\forall\varepsilon>0:\ \exists x_0\in(a,b):\ \forall a<x_1<x_2<x_0:\ \left|\int\limits_{x_1}^{x_2}f\right|<\varepsilon</math>. | ||
* תהא <math>f</math> אינטגרבילית מקומית ב-<math>(a,b]</math>. אם <math>\int\limits_a^b |f|</math> מתכנס אז <math>\int\limits_a^b f</math> מתכנס. | * תהא <math>f</math> אינטגרבילית מקומית ב-<math>(a,b]</math>. אם <math>\int\limits_a^b |f|</math> מתכנס אז <math>\int\limits_a^b f</math> מתכנס. | ||
| + | |||
| + | =סדרות וטורים של פונקציות= | ||
| + | ==התכנסות במ"ש== | ||
| + | ===סדרות=== | ||
| + | * <math>f_n\to f</math> במ"ש על <math>I</math>, כלומר <math>\forall\varepsilon>0:\ \exists n_0\in\mathbb N:\ \forall n>n_0:\ \forall x\in I:\ |f(x)-f_n(x)|<\varepsilon</math>, אם"ם <math>\lim_{n\to\infty}\sup_{x\in I}|f(x)-f_n(x)|=0</math>. | ||
| + | * נניח כי <math>f_n\to f</math> במ"ש ב-<math>I</math>, ועבור <math>x_0\in I</math> כלשהו <math>f_n</math> רציפה ב-<math>x_0</math> לכל <math>n</math>. אזי <math>f</math> רציפה ב-<math>x_0</math>. | ||
| + | * <math>f_n\to f</math> במ"ש ב-<math>[a,b]</math> וכל <math>f_n</math> אינטגרבילית בקטע. אזי <math>f</math> אינטגרבילית בקטע ומתקיים <math>\int\limits_a^b f=\lim_{n\to\infty}\int\limits_a^b f_n</math>. | ||
| + | * <math>\{f_n\}_{n\in\mathbb N}</math> היא סדרת פוקציות בעלות נגזרות רציפות ב-<math>I</math>, המתכנסות במ"ש ב-<math>I</math> לפונקציה <math>g</math>. כמו כן, <math>\{f_n\}</math> מתכנסת בנקודה אחת לפחות ב-<math>I</math>. אזי <math>f=\lim_{n\to\infty} f_n</math> מוגדרת ב-<math>I</math> ומתקיים <math>f'=g</math>. | ||
| + | * סדרת פונקציות <math>\{f_n\}</math> מתכנסת במ"ש אם"ם היא מקיימת את תנאי קושי במ"ש, כלומר <math>\forall\varepsilon>0:\ \exists n_0\in\mathbb N:\ \forall n>m>n_0:\ \forall x\in I:\ |f_n(x)-f_m(x)|<\varepsilon</math>. | ||
| + | ===טורים=== | ||
| + | * טור פונקציות <math>\sum_{n=1}^\infty f_n</math> מתכנס במ"ש אם"ם הוא מקיימת את תנאי קושי במ"ש, כלומר <math>\forall\varepsilon>0:\ \exists n_0\in\mathbb N:\ \forall n>m>n_0:\ \forall x\in I:\ \sum_{k=m}^n f_k(x)<\varepsilon</math>. | ||
| + | * '''מבחן ה-M של ויירשטראס:''' נניח שכל <math>f_n</math> מוגדרת ב-<math>I</math> וחסומה שם, כלומר <math>\forall x\in I:\ |f_n(x)|\le M_n</math> עבור <math>M_n</math> כלשהו, וכן <math>\sum_{n=1}^\infty M_n</math> מתכנס במובן הצר. אזי <math>\sum_{n=1}^\infty f_n</math> מתכנס במ"ש על <math>I</math> | ||
| + | * נתון כי כל <math>f_n</math> רציפה ב-<math>x_0\in I</math> וכן <math>S=\sum_{n=1}^\infty f_n</math> במ"ש על <math>I</math>. אזי <math>S</math> רציפה ב-<math>x_0</math>. | ||
| + | * <math>S=\sum_{n=1}^\infty f_n</math> במ"ש על <math>[a,b]</math> וכל <math>f_n</math> אינטגרבילית ב-<math>[a,b]</math>. אזי <math>S</math> אינטגרבילית בקטע ומתקיים <math>\int\limits_a^b S=\sum_{n=1}^\infty\int\limits_a^b f</math>. | ||
| + | * <math>\{f_n\}_{n\in\mathbb N}</math> היא סדרת פוקציות בעלות נגזרות רציפות ב-<math>I</math>. הטור <math>\sum_{n=1}^\infty f_n</math> מתכנס בנקודה אחת לפחות בקטע, וטור הנגזרות <math>s=\sum_{n=1}^\infty f_n'</math> מתכנס במ"ש על <math>I</math>. אזי <math>\sum_{n=1}^\infty f_n</math> מתכנס במ"ש לפונקציה גזירה <math>S</math> כך ש-<math>S'=s</math>. | ||
| + | |||
| + | ==טורי חזקות== | ||
| + | * יהי <math>\sum_{n=0}^\infty a_n(x-x_0)^n</math> טור חזקות. רדיוס ההתכנסות <math>R=\frac1{\overline{\displaystyle\lim_{n\to\infty}}\sqrt[n]{|a_n|}}</math> מקיים שאם הנקודה <math>x</math> מקיימת <math>|x-x_0|<R</math> אזי הטור מתכנס בהחלט, ואם <math>|x-x_0|>R</math> הטור מתבדר. כמו כן, הטור מתכנס במ"ש ב-<math>[x_0-r,x_0+r]</math> לכל <math>0<r<R</math>. | ||
| + | * יהי <math>\sum_{n=0}^\infty a_n(x-x_0)^n</math> טור חזקות עם רדיוס התכנסות <math>R</math>. אם קיים <math>S=\lim_{n\to\infty}\frac{|a_n|}{|a_{n+1}|}</math> במובן הרחב אזי <math>S=R</math>. | ||
| + | * יהי <math>\sum_{n=0}^\infty a_n(x-x_0)^n</math> טור חזקות עם רדיוס התכנסות <math>R>0</math>. אזי <math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n</math> היא פונציה המוגדרת ב-<math>(x_0-R,x_0+R)</math>, כך שנגזרתה בקטע זה היא <math>f'(x)=\sum_{n=1}^\infty n a_n(x-x_0)^{n-1}</math>. | ||
| + | :* {{הערה|הכללה:}} בתנאים הללו, <math>f</math> גזירה אינסוף פעמים ו-<math>f^{(k)}(x)=\sum_{n=k}^\infty\frac{n!}{(n-k)!}a_n(x-x_0)^{n-k}</math> לכל <math>k\in\mathbb N\cup\{0\}</math>. יתרה מזאת, רדיוס ההתכנסות של הטורים הגזורים הוא <math>R</math>. | ||
| + | * יהי <math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n</math> טור חזקות עם רדיוס התכנסות <math>R>0</math>. אזי לכל <math>n\in\mathbb N\cup\{0\}</math> מתקיים <math>a_n=\frac{f^{(n)}(x_0)}{n!}</math>, ז"א הטור הוא טור טיילור של <math>f</math> סביב <math>x_0</math>. | ||
| + | * יהי <math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n</math> טור חזקות עם רדיוס התכנסות <math>R>0</math>. אזי <math>f</math> אינטגרבילית ב-<math>(x_0-R,x_0+R)</math> ומתקיים לכל <math>x</math> בקטע <math>\int\limits_{x_0}^x f=\sum_{n=0}^\infty \frac{a_n}{n+1}(x-x_0)^{n+1}</math>. רדיוס ההתכנסות של טור האינטגרל הוא <math>R</math>. | ||
| + | * '''משפט היחידות לטורי חזקות:''' אם <math>\sum_{n=0}^\infty a_n(x-x_0)^n=\sum_{n=0}^\infty b_n(x-x_0)^n</math> לכל <math>x\in I\ne\varnothing</math> אזי <math>\forall n:\ a_n=b_n</math>. | ||
| + | * '''משפט אבל:''' נניח ש-<math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n</math> טור חזקות בעל רדיוס התכנסות <math>R</math>. אם <math>\sum_{n=0}^\infty a_nR^n</math> קיים אזי <math>\lim_{x\to x_0+R^-}f(x)</math> קיים ושווה לו, ואם <math>\sum_{n=0}^\infty a_n(-R)^n</math> קיים אזי <math>\lim_{x\to(x_0-R)^+}f(x)</math> קיים ושווה לו. | ||
| + | * '''משפט דיני:''' נתון כי כל <math>f_n</math> רציפה בקטע סגור <math>I</math> והסדרות <math>\{f_n(x)\}_{n\in\mathbb N}</math> עולות לכל <math>x\in I</math> או יורדות לכל <math>x\in I</math>. כמו כן, <math>f_n\to f</math> נקודתית ו-<math>f</math> רציפה ב-<math>I</math>. אזי <math>f_n\to f</math> במ"ש. | ||
| + | |||
| + | =השתנות חסומה= | ||
| + | * תהנה <math>g,h</math> פונקציות מונוטוניות עולות ב-<math>[a,b]</math> ונגדיר <math>f=g-h</math> בקטע. אזי ל-<math>f</math> יש השתנות חסומה בקטע. | ||
| + | * תהי <math>f</math> בעלת השתנות חסומה ב-<math>[a,b]</math>. אזי קיימות פונקציות מונוטוניות עולות <math>g,h</math> בקטע כך ש-<math>f=g-h</math>. | ||
| + | * תהי <math>f</math> בעלת השתנות חסומה ב-<math>[a,b]</math>. אזי לכל <math>x_0\in[a,b)</math> קיים <math>\lim_{x\to x_0^+} f(x)</math> ולכל <math>x_0\in(a,b]</math> קיים <math>\lim_{x\to x_0^-} f(x)</math>. | ||
| + | * תהי <math>f</math> בעלת השתנות חסומה ב-<math>[a,b]</math>. אזי f אינטגרבילית ב-<math>[a,b]</math>. | ||
גרסה מ־18:50, 28 באוגוסט 2011
במשפטים הבאים, אלא אם צויין אחרת, נסמן:
-
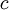 הוא קבוע.
הוא קבוע. -
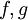 פונקציות.
פונקציות. - הקטע הנתון הוא הקטע הסגור
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. - אם מצויין שלפונקציה יש תכונה מסויימת אזי הכוונה לכך שהתכונה מתקיימת בקטע הנתון (למשל: "
 חסומה" = "
חסומה" = " חסומה ב-
חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ").
"). -
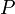 היא חלוקה
היא חלוקה 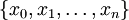 של הקטע הנתון כך ש-
של הקטע הנתון כך ש-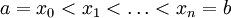 .
.
-
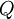 היא העדנה של
היא העדנה של 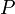 .
. -
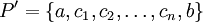 היא חלוקה נוספת של הקטע הנוצרת מהחלוקה
היא חלוקה נוספת של הקטע הנוצרת מהחלוקה 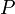 כך ש-
כך ש-![\forall1\le k\le n:\ c_k\in[x_{k-1},x_k]](/images/math/6/9/a/69a81d3601befa0c225b704fa40e9731.png) ו-
ו-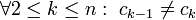 .
.
-
תוכן עניינים
אינטגרלים
- אם
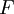 ו-
ו-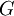 קדומות ל-
קדומות ל- בנקודה כלשהי אז קיים
בנקודה כלשהי אז קיים 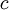 כך ש-
כך ש-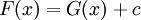 .
. - אם
 חסומה ב-
חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אזי
אזי 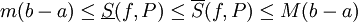 .
. - אם
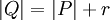 (כלומר,
(כלומר, 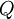 מתקבלת מ-
מתקבלת מ-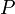 ע"י הוספת
ע"י הוספת 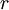 נקודות) ו-
נקודות) ו- חסומה בקטע אזי
חסומה בקטע אזי 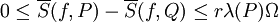 וכן
וכן 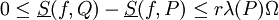 .
. - לכל חלוקה
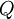 של הקטע הנתון (לאו דווקא העדנה של
של הקטע הנתון (לאו דווקא העדנה של 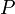 ), אם
), אם  חסומה בקטע אזי
חסומה בקטע אזי 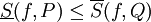 .
. - לכל
 אינטגרבילית מתקיים
אינטגרבילית מתקיים 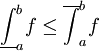 .
. - תהי
 חסומה. אזי
חסומה. אזי 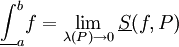 וגם
וגם 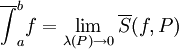 .
. - נניח ש-
 חסומה.
חסומה.  אינטגרבילית אם"ם
אינטגרבילית אם"ם 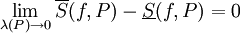 .
. - נניח ש-
 חסומה.
חסומה.  אינטגרבילית אם"ם לכל
אינטגרבילית אם"ם לכל 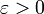 קיימת חלוקה
קיימת חלוקה 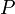 של
של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-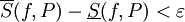 .
. - אם
 רציפה אז
רציפה אז  אינטגרבילית.
אינטגרבילית.
- הכללה: אם
 רציפה וחסומה בקטע הפתוח
רציפה וחסומה בקטע הפתוח 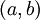 אזי
אזי  אינטגרבילית.
אינטגרבילית.
- הכללה להכללה: אם
 רציפה בקטע בכל נקודה למעט במספר סופי של נקודות והיא חסומה אזי
רציפה בקטע בכל נקודה למעט במספר סופי של נקודות והיא חסומה אזי  אינטגרבילית.
אינטגרבילית.
- הכללה להכללה: אם
- הכללה: אם
- אם
 מונוטונית אזי היא אינטגרבילית.
מונוטונית אזי היא אינטגרבילית. - נניח ש-
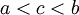 . אזי
. אזי  אינטגרבילית ב-
אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ב-
, ב-![[a,c]](/images/math/2/0/9/209f61583177d88b1f24c85f6a43c6ff.png) וב-
וב-![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) אם"ם היא אינטגרבילית ב-
אם"ם היא אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ואם כן אז
, ואם כן אז 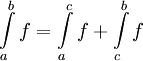 .
.
- הכללה: עבור
 כנ"ל ו-
כנ"ל ו-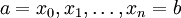 (הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים
(הנקודות לאו דווקא מסודרות בסדר עולה) מתקיים 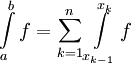 .
.
- הכללה: עבור
- אם
 חסומה אז
חסומה אז 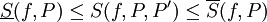 . יתר על כן,
. יתר על כן, 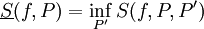 ו-
ו-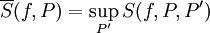 .
. - הגדרות האינטגרל לפי דרבו ולפי רימן שקולות.
- לינאריות: עבור
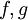 אינטגרביליות מתקיים
אינטגרביליות מתקיים 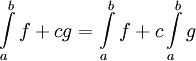 .
. - מונוטוניות: אם
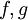 אינטגרביליות וכן
אינטגרביליות וכן ![\forall x\in[a,b]:\ f(x)\ge g(x)](/images/math/b/0/f/b0f5c358a40311d0e8e99133603633c2.png) אזי
אזי 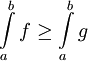 .
.
- חיוביות: בפרט מתקיים שאם
 אינטגרביליות ואי-שלילית אזי
אינטגרביליות ואי-שלילית אזי 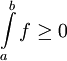 .
.
- חיוביות: בפרט מתקיים שאם
- הכללה לאי-שיוויון המשולש: אם
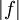 אינטגרבילית אז
אינטגרבילית אז  אינטגרבילית ו-
אינטגרבילית ו-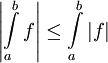 .
. - אם
 אינטגרבילית וחסומה אז
אינטגרבילית וחסומה אז 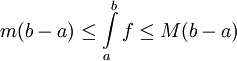 .
.
- מקרה פרטי: אם
![\forall x\in[a,b]:\ |f(x)|\le M](/images/math/1/6/b/16b3029642875feb621b346dca19885e.png) ו-
ו- אינטגרבילית אז
אינטגרבילית אז 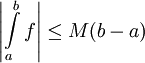 .
.
- מקרה פרטי: אם
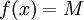 (פונקציה קבועה) אז
(פונקציה קבועה) אז 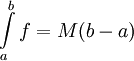 .
.
- מקרה פרטי: אם
- מקרה פרטי: אם
- המשפט היסודי של חשבון אינטגרלי: תהי
 אינטגרבילית ותהי
אינטגרבילית ותהי 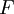 כך ש-
כך ש-![\forall x\in[a,b]:\ F(x):=\int\limits_a^x f](/images/math/0/c/5/0c5f442e2899834dd8dae25116fd3194.png) . אזי
. אזי 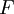 רציפה וכן לכל נקודה ב-
רציפה וכן לכל נקודה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) שבה
שבה  רציפה,
רציפה, 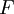 קדומה ל-
קדומה ל- (כלומר,
(כלומר, 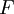 גזירה ב-
גזירה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ו-
ו-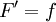 ).
). - נוסחת ניוטון-לייבניץ: תהי
 רציפה. אזי
רציפה. אזי ![\int\limits_a^b f=[F(x)]_{x=a}^b=F(b)-F(a)](/images/math/9/9/1/9910c3fea84d530a4ddc29cee79f0db3.png) .
. - לכל
 רציפה יש פונקציה קדומה.
רציפה יש פונקציה קדומה. - אינטגרציה בחלקים: נניח כי
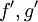 רציפות. אזי
רציפות. אזי 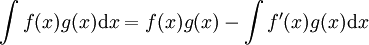 .
.
- שיטת ההצבה:
 .
.
- כל פונקציה רציונלית
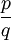 כך ש-
כך ש-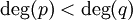 ניתנת לפירוק יחיד כסכום של שברים חלקיים
ניתנת לפירוק יחיד כסכום של שברים חלקיים 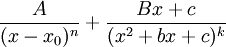 כאשר
כאשר 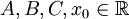 ול-
ול-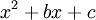 אין שורשים ממשיים.
אין שורשים ממשיים. - נפח גוף הסיבוב הנוצר מסיבוב השטח שמתחת ל-
 אי-שלילית בין
אי-שלילית בין  ל-
ל-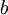 סביב ציר ה-
סביב ציר ה-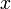 הוא
הוא  .
. - אם
 רציפה אז הממוצע שלה בקטע
רציפה אז הממוצע שלה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 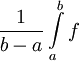 .
. - אם
 בעלת גזירה אז אורך הגרף שלה בקטע
בעלת גזירה אז אורך הגרף שלה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 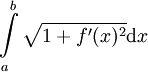 .
. - שטח המעטפת (ללא הבסיסים) של גוף סיבוב הנוצר מסיבוב הגרף של
 רציפה סביב ציר ה-
רציפה סביב ציר ה-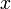 בקטע
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא
הוא 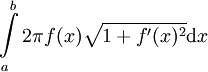 .
. - תהא
 בעלת נגזרת
בעלת נגזרת 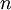 -ית רציפה. אזי
-ית רציפה. אזי 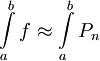 כאשר
כאשר 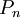 הוא פיתוח טיילור מסדר
הוא פיתוח טיילור מסדר 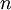 של
של  והשארית היא
והשארית היא 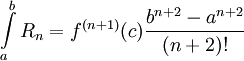 עבור
עבור 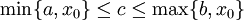 כאשר פיתוח טיילור נעשה סביב
כאשר פיתוח טיילור נעשה סביב 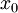 .
. - תהא
 בעלת נגזרת רציפה והחלוקה
בעלת נגזרת רציפה והחלוקה 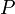 היא חלוקה שווה כאשר לכל
היא חלוקה שווה כאשר לכל 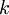 מתקיים
מתקיים 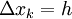 . אזי
. אזי 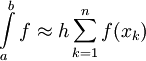 והשארית חסומה ע"י
והשארית חסומה ע"י 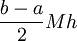 כאשר
כאשר ![M=\max_{x\in[a,b]}\left|f'(x)\right|](/images/math/a/f/5/af58485a1bb5b1e2ba25c07c21c81506.png) .
. - תהא
 בעלת נגזרת שנייה רציפה והחלוקה
בעלת נגזרת שנייה רציפה והחלוקה 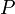 היא חלוקה שווה כאשר לכל
היא חלוקה שווה כאשר לכל 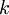 מתקיים
מתקיים 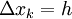 . אזי
. אזי  והשארית חסומה ע"י
והשארית חסומה ע"י 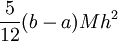 כאשר
כאשר ![M=\max_{x\in[a,b]}\left|f''(x)\right|](/images/math/1/8/2/1821a4640ed7cc006f943ace2590eaa8.png) .
. - תהא
 בעלת נגזרת רביעית רציפה והחלוקה
בעלת נגזרת רביעית רציפה והחלוקה 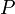 היא חלוקה שווה כאשר לכל
היא חלוקה שווה כאשר לכל 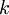 מתקיים
מתקיים 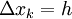 ו-
ו-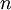 זוגי. אזי
זוגי. אזי  והשגיאה חסומה ע"י
והשגיאה חסומה ע"י 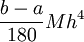 כאשר
כאשר ![M=\max_{x\in[a,b]}\left|f^{(4)}(x)\right|](/images/math/c/0/b/c0b6d228eaf7256cb8ed55af82c13b6e.png) .
. - תהיינה
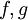 אינטגרביליות ב-
אינטגרביליות ב-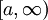 . אזי
. אזי 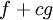 אינטגרבילית ב-
אינטגרבילית ב-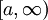 ומתקיים
ומתקיים 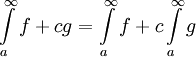 .
. - תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב-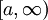 ויהי
ויהי 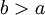 . אזי
. אזי  אינטגרבילית ב-
אינטגרבילית ב-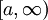 אם"ם
אם"ם  אינטגרבילית ב-
אינטגרבילית ב-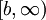 ואם כן
ואם כן 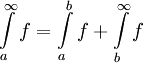 .
. -
 מונוטונית עולה ב-
מונוטונית עולה ב-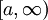 . אזי
. אזי 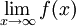 קיים אם"ם
קיים אם"ם 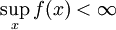 ואם כן
ואם כן 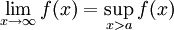 .
. -
 אי-שלילית ואינטגרבילית מקומית ב-
אי-שלילית ואינטגרבילית מקומית ב-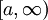 . אזי
. אזי 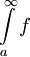 מתכנס אם"ם האינטגרלים החלקיים
מתכנס אם"ם האינטגרלים החלקיים 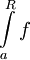 חסומים מלעיל, ואם לא אז
חסומים מלעיל, ואם לא אז 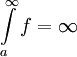 .
. - מבחן ההשוואה: נניח ש-
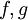 אי-שליליות ואינטגרביליות מקומית ב-
אי-שליליות ואינטגרביליות מקומית ב-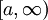 וכן
וכן 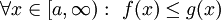 . אם
. אם 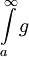 מתכנס אז
מתכנס אז 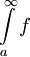 מתכנס.
מתכנס. - מבחן ההשוואה הגבולי:
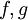 אי-שליליות ואינטגרביליות מקומית ב-
אי-שליליות ואינטגרביליות מקומית ב-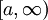 וכן
וכן 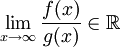 . אם
. אם 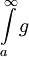 מתכנס אז
מתכנס אז 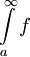 מתכנס.
מתכנס.
- מקרה פרטי: אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד.
- המבחן האינטגרלי לטורים: תהא
 אי-שלילית, מונוטונית יורדת ואינטגרבילית מקומית ב-
אי-שלילית, מונוטונית יורדת ואינטגרבילית מקומית ב-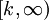 עבור
עבור 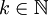 כלשהו. אזי
כלשהו. אזי 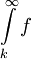 מתכנס אם"ם
מתכנס אם"ם 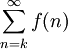 מתכנס.
מתכנס.
- הכללה: בפרט מתקיים
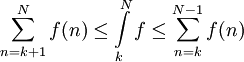 .
.
- הכללה: בפרט מתקיים
- תהא
 מוגדרת ב-
מוגדרת ב-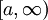 .
. 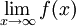 קיים אם"ם הוא מקיים את תנאי קושי בקטע.
קיים אם"ם הוא מקיים את תנאי קושי בקטע. - תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב-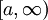 . אזי
. אזי 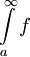 מתכנס אם"ם
מתכנס אם"ם 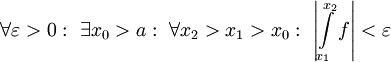 .
. - תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב-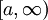 . אם
. אם 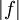 אינטגרבילית בקטע אזי גם
אינטגרבילית בקטע אזי גם  אינטגרבילית בו.
אינטגרבילית בו. - מבחן דיריכלה: תהא
 רציפה ב-
רציפה ב-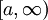 ונניח שהאינטגרלים החלקיים
ונניח שהאינטגרלים החלקיים 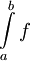 חסומים כאשר
חסומים כאשר 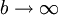 . כמו כן תהא
. כמו כן תהא 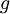 מונוטונית ובעלת נגזרת רציפה ב-
מונוטונית ובעלת נגזרת רציפה ב-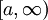 ו-
ו-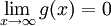 . אזי
. אזי 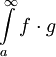 מתכנס.
מתכנס. - סכימה בחלקים:
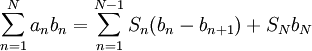 כאשר
כאשר 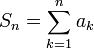 .
. - משפט דיריכלה לטורים: נניח שלטור
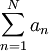 יש סכומים חלקיים חסומים ונניח ש-
יש סכומים חלקיים חסומים ונניח ש-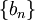 סדרה מונוטונית כך ש-
סדרה מונוטונית כך ש-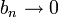 . אזי
. אזי 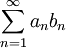 מתכנס.
מתכנס. - אם
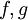 אינטגרביליות ב-
אינטגרביליות ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) אזי לכל
אזי לכל 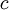 מתקיים
מתקיים 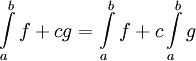 .
. - עבור
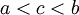 ו-
ו- אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) ,
,  אינטגרבילית בקטע אם"ם
אינטגרבילית בקטע אם"ם  אינטגרבילית ב-
אינטגרבילית ב-![(a,c]](/images/math/0/4/2/0425cdec60417e93bfbb1720291ef9f4.png) , ואם כן
, ואם כן 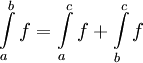 .
. - תהי
 מונוטונית ב-
מונוטונית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אזי
. אזי 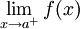 קיים אם"ם
קיים אם"ם  חסומה ב-
חסומה ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) .
. - אם
 אי-שלילית ואינטגרבילית מקומית ב-
אי-שלילית ואינטגרבילית מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) אז
אז  אינטגרבילית ב-
אינטגרבילית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) אם"ם האינטגרלים החלקיים
אם"ם האינטגרלים החלקיים 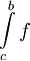 חסומים כאשר
חסומים כאשר 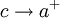 .
. - מבחן ההשוואה:
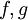 אי-שליליות ואינטגרביליות מקומיות ב-
אי-שליליות ואינטגרביליות מקומיות ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) וכן
וכן ![\forall \in(a,b]:\ f(x)\le g(x)](/images/math/5/8/c/58c4610fb4b7f5aaf8af8d7d532b97a8.png) . אם
. אם 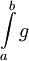 מתכנס אזי
מתכנס אזי 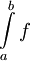 מתכנס.
מתכנס. - מבחן ההשוואה הגבולי:
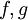 אי-שליליות ואינטגרביליות מקומית ב-
אי-שליליות ואינטגרביליות מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) וקיים
וקיים 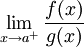 . אם
. אם 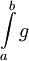 מתכנס אז
מתכנס אז 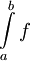 מתכנס.
מתכנס.
- מקרה פרטי: אם בפרט הגבול שונה מ-0 אז שני האינטגרלים מתכנסים ומתבדרים כאחד.
- תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אזי
. אזי 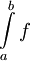 מתכנס אם"ם
מתכנס אם"ם 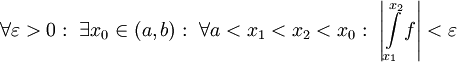 .
. - תהא
 אינטגרבילית מקומית ב-
אינטגרבילית מקומית ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אם
. אם 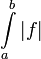 מתכנס אז
מתכנס אז 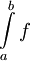 מתכנס.
מתכנס.
סדרות וטורים של פונקציות
התכנסות במ"ש
סדרות
-
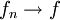 במ"ש על
במ"ש על 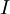 , כלומר
, כלומר 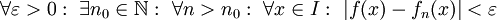 , אם"ם
, אם"ם 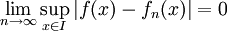 .
. - נניח כי
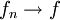 במ"ש ב-
במ"ש ב-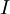 , ועבור
, ועבור 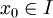 כלשהו
כלשהו 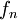 רציפה ב-
רציפה ב-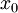 לכל
לכל 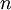 . אזי
. אזי  רציפה ב-
רציפה ב-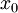 .
. -
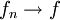 במ"ש ב-
במ"ש ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וכל
וכל 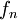 אינטגרבילית בקטע. אזי
אינטגרבילית בקטע. אזי  אינטגרבילית בקטע ומתקיים
אינטגרבילית בקטע ומתקיים 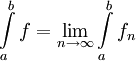 .
. -
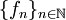 היא סדרת פוקציות בעלות נגזרות רציפות ב-
היא סדרת פוקציות בעלות נגזרות רציפות ב-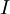 , המתכנסות במ"ש ב-
, המתכנסות במ"ש ב-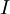 לפונקציה
לפונקציה 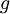 . כמו כן,
. כמו כן, 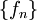 מתכנסת בנקודה אחת לפחות ב-
מתכנסת בנקודה אחת לפחות ב-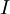 . אזי
. אזי 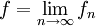 מוגדרת ב-
מוגדרת ב-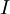 ומתקיים
ומתקיים 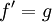 .
. - סדרת פונקציות
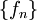 מתכנסת במ"ש אם"ם היא מקיימת את תנאי קושי במ"ש, כלומר
מתכנסת במ"ש אם"ם היא מקיימת את תנאי קושי במ"ש, כלומר 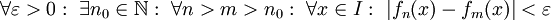 .
.
טורים
- טור פונקציות
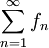 מתכנס במ"ש אם"ם הוא מקיימת את תנאי קושי במ"ש, כלומר
מתכנס במ"ש אם"ם הוא מקיימת את תנאי קושי במ"ש, כלומר 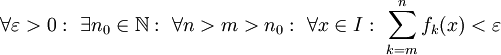 .
. - מבחן ה-M של ויירשטראס: נניח שכל
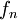 מוגדרת ב-
מוגדרת ב-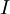 וחסומה שם, כלומר
וחסומה שם, כלומר 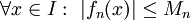 עבור
עבור 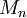 כלשהו, וכן
כלשהו, וכן 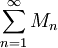 מתכנס במובן הצר. אזי
מתכנס במובן הצר. אזי 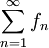 מתכנס במ"ש על
מתכנס במ"ש על 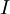
- נתון כי כל
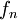 רציפה ב-
רציפה ב-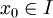 וכן
וכן 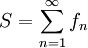 במ"ש על
במ"ש על 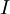 . אזי
. אזי  רציפה ב-
רציפה ב-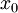 .
. -
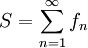 במ"ש על
במ"ש על ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וכל
וכל 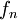 אינטגרבילית ב-
אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי
. אזי  אינטגרבילית בקטע ומתקיים
אינטגרבילית בקטע ומתקיים 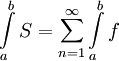 .
. -
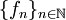 היא סדרת פוקציות בעלות נגזרות רציפות ב-
היא סדרת פוקציות בעלות נגזרות רציפות ב-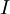 . הטור
. הטור 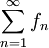 מתכנס בנקודה אחת לפחות בקטע, וטור הנגזרות
מתכנס בנקודה אחת לפחות בקטע, וטור הנגזרות 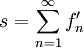 מתכנס במ"ש על
מתכנס במ"ש על 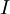 . אזי
. אזי 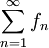 מתכנס במ"ש לפונקציה גזירה
מתכנס במ"ש לפונקציה גזירה  כך ש-
כך ש-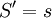 .
.
טורי חזקות
- יהי
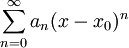 טור חזקות. רדיוס ההתכנסות
טור חזקות. רדיוס ההתכנסות ![R=\frac1{\overline{\displaystyle\lim_{n\to\infty}}\sqrt[n]{|a_n|}}](/images/math/e/6/0/e601eaa980aeb9e0a01773954704f08b.png) מקיים שאם הנקודה
מקיים שאם הנקודה 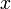 מקיימת
מקיימת 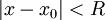 אזי הטור מתכנס בהחלט, ואם
אזי הטור מתכנס בהחלט, ואם 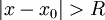 הטור מתבדר. כמו כן, הטור מתכנס במ"ש ב-
הטור מתבדר. כמו כן, הטור מתכנס במ"ש ב-![[x_0-r,x_0+r]](/images/math/a/1/d/a1d1994cd939c738504f99171ece9d05.png) לכל
לכל 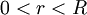 .
. - יהי
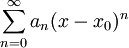 טור חזקות עם רדיוס התכנסות
טור חזקות עם רדיוס התכנסות 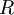 . אם קיים
. אם קיים 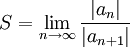 במובן הרחב אזי
במובן הרחב אזי 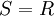 .
. - יהי
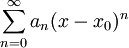 טור חזקות עם רדיוס התכנסות
טור חזקות עם רדיוס התכנסות 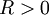 . אזי
. אזי 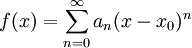 היא פונציה המוגדרת ב-
היא פונציה המוגדרת ב-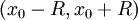 , כך שנגזרתה בקטע זה היא
, כך שנגזרתה בקטע זה היא 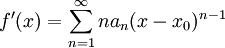 .
.
- הכללה: בתנאים הללו,
 גזירה אינסוף פעמים ו-
גזירה אינסוף פעמים ו-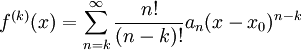 לכל
לכל 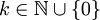 . יתרה מזאת, רדיוס ההתכנסות של הטורים הגזורים הוא
. יתרה מזאת, רדיוס ההתכנסות של הטורים הגזורים הוא 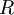 .
.
- הכללה: בתנאים הללו,
- יהי
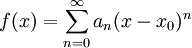 טור חזקות עם רדיוס התכנסות
טור חזקות עם רדיוס התכנסות 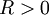 . אזי לכל
. אזי לכל 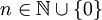 מתקיים
מתקיים 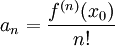 , ז"א הטור הוא טור טיילור של
, ז"א הטור הוא טור טיילור של  סביב
סביב 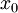 .
. - יהי
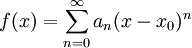 טור חזקות עם רדיוס התכנסות
טור חזקות עם רדיוס התכנסות 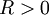 . אזי
. אזי  אינטגרבילית ב-
אינטגרבילית ב-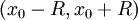 ומתקיים לכל
ומתקיים לכל 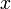 בקטע
בקטע 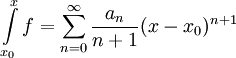 . רדיוס ההתכנסות של טור האינטגרל הוא
. רדיוס ההתכנסות של טור האינטגרל הוא 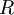 .
. - משפט היחידות לטורי חזקות: אם
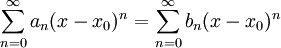 לכל
לכל 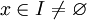 אזי
אזי 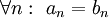 .
. - משפט אבל: נניח ש-
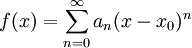 טור חזקות בעל רדיוס התכנסות
טור חזקות בעל רדיוס התכנסות 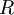 . אם
. אם 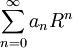 קיים אזי
קיים אזי 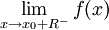 קיים ושווה לו, ואם
קיים ושווה לו, ואם 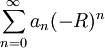 קיים אזי
קיים אזי 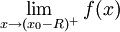 קיים ושווה לו.
קיים ושווה לו. - משפט דיני: נתון כי כל
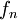 רציפה בקטע סגור
רציפה בקטע סגור 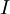 והסדרות
והסדרות 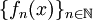 עולות לכל
עולות לכל 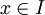 או יורדות לכל
או יורדות לכל 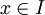 . כמו כן,
. כמו כן, 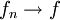 נקודתית ו-
נקודתית ו- רציפה ב-
רציפה ב-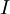 . אזי
. אזי 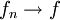 במ"ש.
במ"ש.
השתנות חסומה
- תהנה
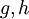 פונקציות מונוטוניות עולות ב-
פונקציות מונוטוניות עולות ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ונגדיר
ונגדיר 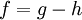 בקטע. אזי ל-
בקטע. אזי ל- יש השתנות חסומה בקטע.
יש השתנות חסומה בקטע. - תהי
 בעלת השתנות חסומה ב-
בעלת השתנות חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי קיימות פונקציות מונוטוניות עולות
. אזי קיימות פונקציות מונוטוניות עולות 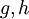 בקטע כך ש-
בקטע כך ש-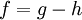 .
. - תהי
 בעלת השתנות חסומה ב-
בעלת השתנות חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי לכל
. אזי לכל 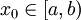 קיים
קיים 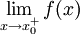 ולכל
ולכל ![x_0\in(a,b]](/images/math/0/5/3/05330cc89261a90eb9fa621176f1554f.png) קיים
קיים 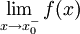 .
. - תהי
 בעלת השתנות חסומה ב-
בעלת השתנות חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי f אינטגרבילית ב-
. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
![\int\limits_a^b f\cdot g'=[f(x)g(x)]_{x=a}^b-\int\limits_a^b f'\cdot g](/images/math/1/9/b/19b8bd99dab83c15e4420a086d20b431.png)