הבדלים בין גרסאות בדף "תחרות חנוכה לינארית 2 תשעב"
(←תשס"ב, מועד ב', שאלה 3 (דה-שליט+ענר)) |
(←תשס"ב, מועד ב', שאלה 3 (דה-שליט+ענר)) |
||
| שורה 90: | שורה 90: | ||
==האוניברסיטה העברית== | ==האוניברסיטה העברית== | ||
| − | === תשס"ב, מועד ב', שאלה | + | === תשס"ב, מועד ב', שאלה 4 (דה-שליט+ענר) === |
מצא את צורת הז'ורדן של המטריצה | מצא את צורת הז'ורדן של המטריצה | ||
<math>\begin{pmatrix} | <math>\begin{pmatrix} | ||
גרסה מ־11:33, 18 בדצמבר 2011
תוכן עניינים
תחרות חנוכה, לינארית 2 תשע"ב: שאלות ממבחנים, בנושא צורת ג'ורדן, עם פתרונות
הנחיות
0. קרא בעיון את החוברת על משפט ג'ורדן, כולל התירגול בסוף. פתרונות שיהיו מסובכים יותר מהשיטה הפשוטה שנלמדת בחוברת, לא יתקבלו.
1. חפש מבחנים באלגברה לינארית המכילים שאלות בנושא צורת ג'ורדן. למשל, יש בחינות במאגר הבחינות של ד"ר צבאן.
2. אם המבחן שמצאת אינו במאגר הבחינות של ד"ר צבאן, שלח לו עותק של המבחן באימייל (tsaban@math.biu.ac.il), כדי שיתווסף למאגר.
3. מצא במבחן זה שאלה שפתרונה דורש שימוש בכלים של צורת ג'ורדן, אשר טרם נכתבה להלן. כתוב את השאלה להלן, תחת כותרת האוניברסיטה המתאימה, והוסף קישור לפתרון, לפי הדוגמאות להלן. אפשר לעשות זאת על ידי העתקת הדוגמא להלן ושינוי הפרטים.
4. כל תלמיד שהעלה שאלה ופתרון מלא שלה, בלי טעויות, זוכה בשאלה זו. המטרה היא לזכות בכמה שיותר שאלות. בסוף התחרות, נפרסם דירוג של התלמידים, לפי מספר השאלות שפתרו. (תלמידים שלא יזכו בשאלות, ימוקמו אחרונים.)
שיתוף פעולה: תלמידים המעוניינים לשתף פעולה ולהעלות פתרון יחד (למשל, אם אחד יודע רק לקרוא והשני רק לכתוב) יכולים לעשות זאת, אך אז הניקוד על השאלה (נקודה אחת) יתחלק ביניהם בשווה. עדיין, זה עשוי להשתלם להם, אם יחד הם יפתרו יותר מאשר הסכום של מספר הפתרונות שכל אחד יכול להעלות לבד. וגם זה עשוי להיות יותר כיף.
שבת מנוחה: כדי לא לצאת מפרופורציות, וכדי שהתחרות תהיה הוגנת כלפי כל התלמידים, שאלות שיעלו בשבת (מזמן הדלקת הנרות ביום שישי ועד מוצאי שבת) לא יזכו בניקוד.
5. יש להעלות את הפיתרון בתוך הויקי (להלן דוגמא איך מעלים פתרון בויקי), ולא על ידי צירוף קובץ עם הפתרון. צירוף קובץ עם הפתרון אפשרי רק כדי לשמור את השאלה לעצמכם, אבל לא יזכה בנקודה כל עוד לא העליתם את הפתרון בויקי. לעזרה ראה: איך כותבים בויקי.
6. תלמיד שמצא שגיאה בפתרון קודם, יתאר את השגיאה בצורה ברורה בדף השיחה, ויתקנה, יזכה בשאלה וינשל את הפותר המקורי מבעלותו על שאלה זו. תיקון שגיאות כתיב אף הוא יבורך, אך אינו מזכה בשאלה. רק תיקון טעות של ממש בפיתרון נחשב לצורך הזיכוי.
7. ייתכן שינתנו פרסים סימליים (אחד או יותר) לזוכים במקומות הראשונים, או בונוס בציון לפי המיקום ברשימה. בכל אופן, המופיעים במקומות הראשונים יזכו לכבוד רב!
- לנוחיותכם, להלן תבנית להעלאת שאלה. השלבים:
א. פיתחו תבנית זו על ידי הקלקה על "עריכה".
ב. העתיקו את תוכנה למקום שבו אתם מכניסים את השאלה החדשה שלכם, ושנו את הנתונים בהתאם.
ג. לחצו על כפתור "שמירה" שבתחתית חלון העריכה.
ד. הקישור לפיתרון יופיע בצבע אדום. הקליקו עליו וייפתח דף התשובה לשאלה. שם, רישמו את תשובתכם ושימרו (לחצו על כפתור "שמירה" שבתחתית חלון העריכה.).
זה הכל.
תש?"?, מועד א/ב', שאלה ? (מרצה+מרצה)
להכניס כאן את השאלה.
אוניברסיטת בר-אילן
תשע"א, מועד א', שאלה 4 (צבאן+קוניאבסקי)
נניח שלמטריצות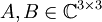 
יש אותו פולינום אופייני, וכן אותו פולינום מינימלי, הוכח שהמטריצות A וB דומות.
תשנ"א, מועד ב', שאלה 4 (מינה טייכר)
מצא צורת ז'ורדן ל-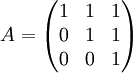 
. (כן, גם אני לא האמנתי שזה כל התרגיל בהתחלה.)
תשס"ב, מועד ב', שאלה 2 ברב-ברירתיות (ד"ר בועז צבאן)
תשס"ב, מועד א', שאלה 6 (בועז צבאן)
האוניברסיטה העברית
תשס"ב, מועד ב', שאלה 4 (דה-שליט+ענר)
מצא את צורת הז'ורדן של המטריצה
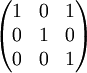מעל שדה המרוכבים
קישור למקור: http://u.cs.biu.ac.il/~tsaban/LinearAlgebra/Exams/HU_LA2/80135_2002_2_2_1.pdf
תשס"ט, מועד ב', שאלה 4 (ורשבסקי+רומיק)
נתונות המטריצות
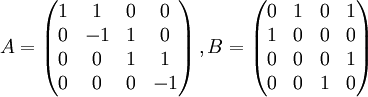
האם הן דומות? הוכח את טענתך.
מדיה:Targil.jpg (נפתלי)
נפתלי, כתוב כאן הפתרון שלך כדי לקבל את הניקוד (ב.צ.): פתרון (נפתלי)
תשס"ט, מועד א', שאלה 4 (ורשבסקי+רומיק)
נתונה המטר':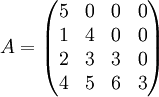 
א) מצא את צורת ז'ורדן של A
ב) מצא P הפיכה כך ש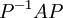 
היא צורת זורדן של A.
מקור: [1]
הערה: מי שיוסיף, בקישור הבא, פתרון סטנדרטי יותר לפי החוברת בנושא משפט ג'ורדן שהעליתי לאתר הקורס, יזכה גם הוא בנקודה על שאלה זו. (בועז)
(הוספתי את הפתרון שאני חושב שהתכוונת אליו, אשמח לאישור, אוהד קליין)
תשס"ה, מועד ב', שאלה 11 (מוזס+סלע)
שאלה: תהי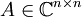 
. הוכיחו כי 
.
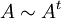תשס"ד, מועד ב, שאלה 11 (איזנברג+סלע)
השאלה:
תהי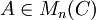 
המטר' הבאה: 
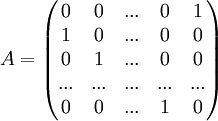. מצא את צורת הז'ורדן שלה.
מקור: [2]
