הבדלים בין גרסאות בדף "27-221 מד"ר למדעי המח חורף תשעב"

גרסה מ־20:47, 27 בדצמבר 2011

27-221 מד"ר למדעי המח

מרצה: ד"ר ודים אוסטפנקו

מתרגל: אדם צ'פמן

ראו גם:

נושאים מרכזיים

חבורה, מונויד, חבורה למחצה (אגודה).

הודעות כלליות

פתחתי סוף-סוף דף לקורס. אעלה לכאן מעתה את מערכי השיעור (לפחות את עיקרי הדברים) לפני השיעור עצמו על-מנת שיהיה קל יותר לעקוב אחרי מה שנעשה. יקח קצת זמן אך גם אעלה רטרואקטיבית את מערכי השיעור שכבר התקיימו.Adam Chapman 22:43, 27 בדצמבר 2011 (IST)
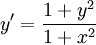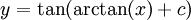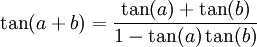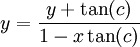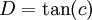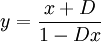בקשר לתרגיל שהוצג בכיתה $y'=\frac{1+y^2}{1+x^2}$ , הגענו בכיתה לתשובה $y=\tan(\arctan(x)+c)$ ולא פיתחנו אותה הלאה. ישנן זהויות טריגונומטריות (אעלה דף עם החשובות ביניהן) שאחת מהן היא $\tan(a+b)=\frac{\tan(a)+\tan(b)}{1-\tan(a) \tan(b)}$ . אם משתמשים בזה אז מקבלים $y=\frac{y+\tan(c)}{1-x \tan(c)}$ ואם מסמנים $D=\tan(c)$ אז מקבלים $y=\frac{x+D}{1-D x}$ .Adam Chapman 22:43, 27 בדצמבר 2011 (IST)

@@ שורה 20: / שורה 20: @@
 == הודעות כלליות ==
 * פתחתי סוף-סוף דף לקורס. אעלה לכאן מעתה את מערכי השיעור (לפחות את עיקרי הדברים) לפני השיעור עצמו על-מנת שיהיה קל יותר לעקוב אחרי מה שנעשה. יקח קצת זמן אך גם אעלה רטרואקטיבית את מערכי השיעור שכבר התקיימו.[[משתמש:Adam Chapman|Adam Chapman]] 22:43, 27 בדצמבר 2011 (IST)
-* בקשר לתרגיל שהוצג בכיתה <math>y'=\frac{1+y^2}{1+x^2}</math>, הגענו בכיתה לתשובה <math>y=\tan(\arctan(x)+c)</math> ולא פיתחנו אותה הלאה. ישנן זהויות טריגונומטריות (אעלה דף עם החשובות ביניהן) שאחת מהן היא <math>\tan(a+b)=\frac{\tan(a)+\tan(b)}{1-\tan(a) \tan(b)}</math>. אם משתמשים בזה אז מקבלים <math>y=\frac{y+\tan(c)}{1-x \tan(c)}</math> ואם מסמנים <math>D=\tan(c)</math> אז מקבלים <math>y=\frac{x+D}{1-x D}</math>.[[משתמש:Adam Chapman|Adam Chapman]] 22:43, 27 בדצמבר 2011 (IST)
+* בקשר לתרגיל שהוצג בכיתה <math>y'=\frac{1+y^2}{1+x^2}</math>, הגענו בכיתה לתשובה <math>y=\tan(\arctan(x)+c)</math> ולא פיתחנו אותה הלאה. ישנן זהויות טריגונומטריות (אעלה דף עם החשובות ביניהן) שאחת מהן היא <math>\tan(a+b)=\frac{\tan(a)+\tan(b)}{1-\tan(a) \tan(b)}</math>. אם משתמשים בזה אז מקבלים <math>y=\frac{y+\tan(c)}{1-x \tan(c)}</math> ואם מסמנים <math>D=\tan(c)</math> אז מקבלים <math>y=\frac{x+D}{1-D x}</math>.[[משתמש:Adam Chapman|Adam Chapman]] 22:43, 27 בדצמבר 2011 (IST)

הבדלים בין גרסאות בדף "27-221 מד"ר למדעי המח חורף תשעב"

גרסה מ־20:47, 27 בדצמבר 2011

נושאים מרכזיים

הודעות כלליות

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים