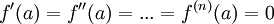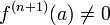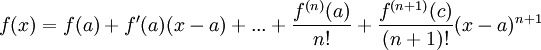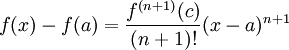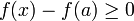הבדלים בין גרסאות בדף "סיווג נקודה חשודה"
מתוך Math-Wiki
(←סיווג נקודות חשודות) |
(←סיווג נקודות חשודות) |
||
| שורה 5: | שורה 5: | ||
==סיווג נקודות חשודות== | ==סיווג נקודות חשודות== | ||
| + | '''משפט.''' תהי f פונקציה הגזירה '''ברציפות''' n+1 פעמים בסביבת הנקודה a. עוד נניח כי | ||
| + | ::<math>f'(a)=f''(a)=...=f^{(n)}(a)=0</math> | ||
| + | |||
| + | ::<math>f^{(n+1)}(a)\neq 0</math> | ||
| + | |||
| + | אזי: | ||
| + | *אם n+1 זוגי וגם <math>f^{(n+1)}(a)>0</math>אזי a '''[[נקודת קיצון|נקודת מינימום מקומי]]''' | ||
| + | *אם n+1 זוגי וגם <math>f^{(n+1)}(a)<0</math>אזי a '''[[נקודת קיצון|נקודת מקסימום מקומי]]''' | ||
| + | *אם n אי זוגי אזי a [[נקודת פיתול]] | ||
| + | |||
| + | |||
| + | '''הוכחה.''' | ||
| + | |||
| + | |||
| + | לפי [[משפט טיילור עם שארית לגראנז'|טיילור]] לכל x בסביבה קיימת נקודה c בין x לבין a כך ש: | ||
| + | |||
| + | ::<math>f(x)=f(a)+f'(a)(x-a)+...+\frac{f^{(n)}(a)}{n!}+\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}</math> | ||
| + | |||
| + | אבל לפי ההנחה כי n הנגזרות הראשונות מתאפסת ב-a, מתקיים | ||
| + | |||
| + | ::<math>f(x)-f(a)=\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}</math> | ||
| + | |||
| + | לכן, אם n+1 זוגי וגם <math>f^{(n+1)}(a)>0</math> לפי רציפות הנגזרת השנייה קיימת סביבה של a בה <math>f^{(n+1)}>0</math> ולכן לכל x בסביבה זו מתקיים: | ||
| + | |||
| + | ::<math>f(x)-f(a)\geq 0</math> | ||
| + | |||
| + | שכן <math>(x-a)^{(n+1)}\geq 0</math> תמיד עבור n+1 זוגי. | ||
| + | |||
| + | |||
| + | כלומר אם <math>f^{(n+1)}(a)>0</math> אזי x הינה '''[[נקודת קיצון|נקודת מינימום]]''' | ||
| + | |||
| + | באופן דומה, אם <math>f^{(n+1)}(a)<0</math> אזי x הינה '''[[נקודת קיצון|נקודת מקסימום]]''' | ||
| + | |||
| + | |||
| + | אם n+1 אי זוגי, אזי הסימן של <math>(x-a)^{(n+1)}</math> חיובי בסביבה ימנית של a ושלילי משמאלה. | ||
| + | |||
| + | לכן באופן | ||
גרסה מ־21:47, 7 במרץ 2012
הגדרת נקודה חשודה
תהי f פונקציה ממשית. נקודה x בתחום ההגדרה של f נקראת חשודה אם  או שהנגזרת אינה מוגדרת ב-x
או שהנגזרת אינה מוגדרת ב-x
סיווג נקודות חשודות
משפט. תהי f פונקציה הגזירה ברציפות n+1 פעמים בסביבת הנקודה a. עוד נניח כי
אזי:
- אם n+1 זוגי וגם
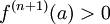 אזי a נקודת מינימום מקומי
אזי a נקודת מינימום מקומי - אם n+1 זוגי וגם
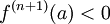 אזי a נקודת מקסימום מקומי
אזי a נקודת מקסימום מקומי - אם n אי זוגי אזי a נקודת פיתול
הוכחה.
לפי טיילור לכל x בסביבה קיימת נקודה c בין x לבין a כך ש:
אבל לפי ההנחה כי n הנגזרות הראשונות מתאפסת ב-a, מתקיים
לכן, אם n+1 זוגי וגם 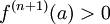 לפי רציפות הנגזרת השנייה קיימת סביבה של a בה
לפי רציפות הנגזרת השנייה קיימת סביבה של a בה 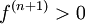 ולכן לכל x בסביבה זו מתקיים:
ולכן לכל x בסביבה זו מתקיים:
שכן 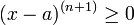 תמיד עבור n+1 זוגי.
תמיד עבור n+1 זוגי.
כלומר אם 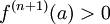 אזי x הינה נקודת מינימום
אזי x הינה נקודת מינימום
באופן דומה, אם 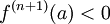 אזי x הינה נקודת מקסימום
אזי x הינה נקודת מקסימום
אם n+1 אי זוגי, אזי הסימן של 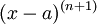 חיובי בסביבה ימנית של a ושלילי משמאלה.
חיובי בסביבה ימנית של a ושלילי משמאלה.
לכן באופן